p-E-凸集及其若干性质

刘卫锋

(郑州航空工业管理学院 数理系 河南 郑州 450015)

p-E-凸集及其若干性质

刘卫锋

(郑州航空工业管理学院 数理系 河南 郑州 450015)

在p-凸集和E-凸集概念基础上，通过将p-凸集和E-凸集相结合，提出了一种广义凸集——p-E-凸集,使得凸集、p-凸集和E-凸集成为它的特例，推广了凸集的概念.最后，初步研究了p-E-凸集的性质.

凸集；p-E-凸集；p-凸集；E-凸集

0 引言

由于凸集及其性质在凸分析、函数论、最优化理论等数学分支中均有广泛应用[1-5]，因此，凸集的研究和推广一直是数学应用基础研究领域的重要课题.在凸集概念基础上，文[1-3]引进了p-凸集和绝对p-凸集；文[6]对p-凸集和绝对p-凸集的性质进行了较为系统的研究；文[7]提出了p-完美凸集和绝对p-完美凸集；文[8]通过弱化凸集和凸函数定义的条件，引入了E-凸集和E-凸函数等概念；文[9-10]指出文[8]中存在的错误，完善了E-凸集和E-凸函数；文[11]对E-凸集的性质进行较为系统的研究；文[12]提出了拟E-凸和严格拟E-凸函数的概念，并对其性质进行了研究;文[13]进一步给出了半强E-凸函数的概念；文[14]研究了E-凸集，E-凸函数和半E-凸函数的性质；文[15]研究了中点E-凸函数、E-拟凸函数及其性质；文[16]研究了E-凸函数的方向导数；文[17]给出了E-凸函数的一个性质.事实上，上述凸集的推广大致可以分为两类：一类是将凸集中任意两点x,y的凸组合的系数λ,1-λ推广α,β，其中α,β≥0,p∈(0,1],αp+βp=1， 即p-凸集和p-凸函数及其推广；一类是将凸集中任意两点x,y推广为映射E的像E(x),E(y)，即E-凸集和E-凸函数及其推广.但是，将上述两类广义凸集相结合的研究报道并未见到.鉴于此，本文将p-凸集和E-凸集相结合，得到一种广义凸集——p-E-凸集，使得凸集、p-凸集和E-凸集成为它的特例，拓展了凸集的概念.最后，研究了p-E-凸集的性质.

1 相关概念

定义1[1]设集合M⊂Rn，若∀x,y∈M,∀λ∈[0,1]，有λx+(1-λ)y∈M，则称M为凸集.

定义2[1-3]设集合M⊂Rn，若∀x,y∈M,α,β≥0,p∈(0,1],αp+βp=1，有αx+βy∈M，则称M为p-凸集.

定义3[6]设集合M⊂Rn，记

则称Cp(M)为M的p-凸包.

定义4[8]设集合M⊂Rn，若存在映射E:Rn→Rn，使得∀x,y∈M,∀λ∈[0,1]，有λE(x)+

(1-λ)E(y)∈M，则称M为E-凸集.

2 p-E-凸集的概念

定义5 设集合M⊂Rn，若存在映射E:Rn→Rn,使得∀x,y∈M,α,β≥0,p∈(0,1],αp+βp=1,有αE(x)+βE(y)∈M，则称M为p-E-凸集.

定理1 任意E-凸集是p-E-凸集，任意p-凸集是p-E-凸集，任意凸集是p-E-凸集.

证明 (1)设M是任意E-凸集，由定义4可知，存在映射E:Rn→Rn，使∀x,y∈M,∀λ∈[0,1]，有λE(x)+(1-λ)E(y)∈M.令α=λ,β=1-λ，取p=1∈(0,1]，则αp+βp=1，于是有

αE(x)+βE(y)=λE(x)+(1-λ)E(y)∈M.

由定义5可知，M是p-E-凸集.

(2)设M是任意p-凸集，由定义2可知，∀x,y∈M,α,β≥0,p∈(0,1],αp+βp=1，有αx+βy∈M.令

E:Rn→Rn,E(x)=x,∀x∈Rn,

则

∀x,y∈M,α,β≥0,p∈(0,1],αp+βp=1，

有

αE(x)+βE(y)=αx+βy∈M.

由定义5可知，M是p-E-凸集.

(3)设M是任意凸集，由定义1可知，∀x,y∈M,∀λ∈[0,1]，有λx+(1-λ)y∈M.令

E:Rn→Rn,E(x)=x,∀x∈Rn,

同时令α=λ,β=1-λ，取p=1∈(0,1]，则αp+βp=1，于是有

αE(x)+βE(y)=λx+(1-λ)y∈M.

由定义5可知，M是p-E-凸集.

定理2 设集合M⊂Rn是p-E-凸集，则E(M)⊆M.

证明 由于M是p-E-凸集，则存在映射E:Rn→Rn,使得∀x,y∈M,α,β≥0,p∈(0,1]，αp+βp=1，有αE(x)+βE(y)∈M.显然，当β=0时，有αp=1，由于p∈(0,1]，因此必有α=1，故有E(x)=αE(x)+βE(y)∈M，考虑到x的任意性，即有E(M)⊆M.

类似地，当α=0时，也可证明E(M)⊆M.

下面讨论p-E-凸集的几个等价条件.

定理3 设集合M⊂Rn,下面几个条件彼此等价：

(1)M是p-E-凸集；

(2)∀x,y∈M,t∈[0,1],有t1/pE(x)+(1-t)1/pE(y)∈M；

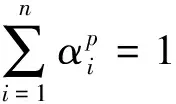
证明 先证(1)⟹(2).由M是p-E-凸集知,存在映射E:Rn→Rn,使得∀x,y∈M,α,β≥0,p∈(0,1],αp+βp=1,有αE(x)+βE(y)∈M.令t=αp，则得到α=t1/p,β=(1-t)1/p，显然有t∈[0,1],且t1/pE(x)+(1-t)1/pE(y)∈M.所以，(1)⟹(2)成立.

再证(2)⟹(3).对n施行数学归纳法.

当i=1时，令α1=t=1，则有tE(x)=αE(x)=E(x)∈M.

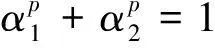
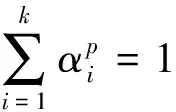
若αk+1=1，则α1=α2=…=αk=0，于是由归纳假设和定理2可知，

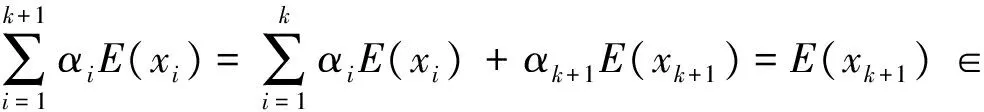
所以，(2)⟹(3)成立.

最后证(3)⟹(1). 只需令i=2，即可得到M是p-E-凸集.

3 p-E-凸集的若干性质

定理4 设集合M⊂Rn是p-E1-凸集，且是p-E2-凸集，则M是p-(E1∘E2)-凸集，也是p-(E2∘E1)-凸集，其中E1:Rn→Rn,E2:Rn→Rn，E1∘E2,E2∘E1分别为映射E2与E1，E1与E2的复合运算.

证明 假设x,y∈M，α,β≥0,p∈(0,1],αp+βp=1，有α(E1∘E2)(x)+β(E1∘E2)(y)∉M，即α(E1(E2(x)))+β(E1(E2(y)))∉M.

考虑到M是p-E2-凸集，由定理2知E2(M)⊆M，因此E2(x),E2(y)∈M.然后考虑到M是p-E1-凸集，再由定理2知E1(E2(x)),E1(E2(y))∈M，且α,β≥0,p∈(0,1],αp+βp=1，有α(E1(E2(x)))+β(E1(E2(y)))∈M.这与α(E1(E2(x)))+β(E1(E2(y)))∉M矛盾.故M是p-(E1∘E2)-凸集.

同理可证，M是p-(E2∘E1)-凸集.

定理5 设集合M,N⊂Rn是p-E-凸集，则M∩N是p-E-凸集.

证明 ∀x,y∈M∩N，则有x,y∈M且x,y∈N.由于M,N是p-E-凸集，故存在E:Rn→Rn，使α,β≥0,p∈(0,1],αp+βp=1,有αE(x)+βE(y)∈M且αE(x)+βE(y)∈N，于是αE(x)+βE(y)∈M∩N.所以,M∩N是p-E-凸集.

可以将定理5推广至任意多个集合.

证明 与定理5证明类似，略.

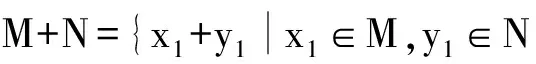
证明 ∀x,y∈M+N，则存在x1,x2∈M,y1,y2∈N，使得x=x1+y1,y=x2+y2.由于M,N是p-E-凸集，因此存在E:Rn→Rn，使得α,β≥0,p∈(0,1],αp+βp=1,有αE(x1)+βE(x2)∈M且αE(y1)+βE(y2)∈N.考虑到E是线性映射，于是有

αE(x1+y1)+βE(x2+y2) =α(E(x1)+E(y1))+β(E(x2)+E(y2))

=(αE(x1)+βE(x2))+(αE(y1)+βE(y2))∈M+N.

所以,M+N是p-E-凸集.

证明 ∀x,y∈kM，则∃x1,x2∈M，使x=kx1,y=kx2.由于M是p-E-凸集，故存在E:Rn→Rn，使得α,β≥0,p∈(0,1],αp+βp=1,有αE(x1)+βE(x2)∈M.考虑到E是线性映射，于是有

αE(x)+βE(y) =α(E(kx1)+E(kx2))

=k(αE(x1)+βE(x2))∈kM.

所以kM是p-E-凸集.

可将定理7和定理8推广至一般情况.

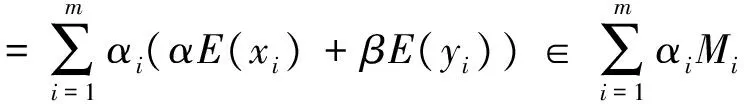
定义6 设集合M⊂Rn，记

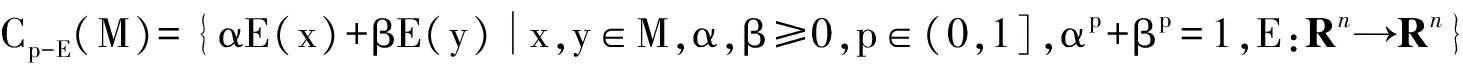
则称Cp-E(M)为M的p-E凸包.

显然，当E为恒等映射时，M的p-E凸包Cp-E(M)就是p凸包Cp(M).

定理10 设集合M⊂Rn，则Cp-E(M)是Rn中包含M的最小p-E-凸集，也是所有包含M的p-E-凸集的交集.

证明 如果

则因为

=αp+βp=1,

故有

α(α1E(x1)+β1E(y1))+β(α2E(x2)+β2E(y2)) =αα1E(x1)+αβ1E(y1)+

βα2E(x2)+ββ2E(y2)∈Cp-E(M).

若p-E-凸集N⊃M，则由Cp-E(M)的定义可知，N⊃Cp-E(M)，因此，Cp-E(M)是包含M的最小p-E-凸集.又由定理6可知，p-E-凸集的交集仍为p-E-凸集，所以Cp-E(M)是全体包含M的p-E-凸集的交集.

定理11 设V,W是线性空间，L:V→W,E:Rn→Rn均是线性映射，则

(1)若M⊂V是p-E-凸集，则L(M)⊂W是p-E-凸集；

(2)若T⊂W是p-E-凸集，则L-1(T)⊂V是p-E-凸集.

证明 (1)∀y1,y2∈L(M)，则∃x1,x2∈M，使得y1=L(x1),y2=L(x2)，因为M是p-E-凸集，因此α,β≥0,p∈(0,1],αp+βp=1,有αE(x1)+βE(x2)∈M.又由L是线性映射，可得

αE(y1)+βE(y2) =αE(L(x1))+βE(L(x2))

=L(αE(x1)+βE(x2))∈L(M),

所以，L(M)是p-E-凸集.

(2)∀x1,x2∈L-1(T)，则∃y1,y2∈T，使得x1=L-1(y1),x2=L-1(y2)，因为T是p-E-凸集，因此α,β≥0,p∈(0,1],αp+βp=1,有αE(y1)+βE(y2)∈T.

考虑到L-1是线性映射，可得

αE(x1)+βE(x2) =αE(L-1(y1))+βE(L-1(y2))

=L-1(αE(y1)+βE(y2))∈L-1(T).

所以，L-1(T)是p-E-凸集.

[1] Köthe G. Topological Vector Space[M]. Berlin:Springer-Verlag,1983:160-178.

[2] Smon S. The sequence spacesl(pv)andm(pv)[J]. Proceedings of the London Mathematical Society,1965, 15(3): 422-436.

[3] 定光桂.拓扑线性空间选讲[M].南宁:广西教育出版社,1987:62-98.

[4] 袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1997.

[5] 胡适耕.泛函分析[M].北京:科学出版社,2001.

[6] 刘文，王晶昕.p-凸集和绝对p-凸集的一些性质[J].辽宁师范大学学报:自然科学版,1995,18(1):5-9.

[7] 张端,刘旭飞,冷岗松.p-完美凸集和绝对p-完美凸集[J].上海大学学报:自然科学版,2010,16(3):262-267.

[8] Youness E A.E-convex sets,E-convex functions, andE-convex programming[J].Journal of Optimization Theory and Applications,1999,102(2):439-450.

[9] Yang X M. OnE-convex set,E-convex functions, andE-convex programming[J].Journal of Optimization Theory and Applications,2001,109(3):699-704.

[10] Jian J B. Incorrect result forE-convex functions, andE-convex programming[J]. Mathematical Research and Exposition,2003,23(3):461-466.

[11] Sheiba Grace J, Thangavelu P. Properties ofE-convex sets[J]. Tamsui Oxford Journal of Mathematical Sciences,2009,25(1):1-7.

[12] Youness E A. Quasi and strictly quasiE-convex functions[J]. Statistics and Management Systems, 1999, 4(2): 201-210.

[13] Youness E A, Tarek E. Semi stronglyE-convex functions[J]. Journal of Mathematics and Statistics, 2005, 1(1): 51-57.

[14] 黄应全,赵克全.E-凸集,E-凸函数和半E-凸函数[J].河北大学学报:自然科学版,2005,25(1): 13-15.

[15] 宁刚.E-凸函数的若干特征[J].运筹学学报,2007,11(1):121-126.

[16] 景书杰，宋虹颖.E-凸函数的方向导数[J].吉林师范大学学报:自然科学版，2009,30(1):15-18.

[17] 景书杰，宋虹颖.E-凸函数的一个性质[J].河南理工大学学报:自然科学版，2008,27(6):740-742.

p-E-Convex Set and Its Properties

LIU Wei-feng

(DepartmentofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China)

Based on the concepts ofp-convex sets andE-convex sets, a generalized convex set defined asp-E-convex set was proposed by combiningp-convex sets withE-convex sets, so thatp-convex sets,E-convex sets and convex sets were made particular cases, and the concept of a convex sets was generalized. Some properties ofp-E-convex sets were investigated.

convex set;p-E-convex set;p-convex set;E-convex set

2013-03-28

河南省教育厅科学技术研究重点项目，编号12B110027.

刘卫锋(1976-)，男，讲师，硕士，主要从事数学建模研究，E-mail:lwf0519@163.com.

O 221.2

A

1671-6841(2014)01-0028-05

10.3969/j.issn/1671-6841.2014.01.007