一种变步长NLMS-OCF算法的研究

李 茹，张 骏，智永锋

（西北工业大学 自动化学院，陕西 西安 710072）

一种变步长NLMS-OCF算法的研究

李 茹，张 骏，智永锋

（西北工业大学 自动化学院，陕西 西安 710072）

为了提高自适应滤波器的性能，提出了一种变步长的NLMS-OCF算法，直接将投影误差范数通过指数函数的映射得到平滑因子，进而对步长进行控制。仿真结果表明，相对于传统的NLMS-OCF算法，改进的算法获得了更好的收敛速度和稳态误差。

自适应滤波器；NLMS-OCF算法；变步长；收敛速度；稳态误差

归一化最小均方(Normalized Least Mean Square,NLMS)算法由于其低运算量和易于实现而得到了广泛的应用。然而，对于高度自相关的输入信号，此算法的收敛速度表现出了明显的下降。仿射投影算法（Affine Projection Algorithm,APA）通过重复的利用过去的输入信号很好地解决了上述问题[1-2]。但是步长的选择会影响算法收敛速度和失调量之间的关系，传统的NLMS和APA算法利用定步长很难找到快收敛和低失调之间的平衡点，因此需要使用变步长来进行调整。文献[3]通过最小化每次迭代的均方偏差获得NLMS算法的最优步长。文献[4]提出了一种变步长的APA（Variable Step-size Affine Projection Algorithm, VS-APA）算法，该算法获得了比较高的估计精度，但是收敛速度相对缓慢。文献[5]提出了一种基于时变平滑因子的VS-APA（Variable Step-size Affine Projection Algorithm With Variable Smoothing Factor,VS-APA-VSF）算法，该算法利用投影误差向量的范数作为判断优化距离的准则，但是它需要根据投影误差范数的变化趋势确定“触发点”，增加了实现的复杂性。文献[6]提出了一种基于指数型平滑因子的VS-APA（Variable Step-size Affine Projection Algorithm With Exponential Smoothing Factors,VS-APA-EXP）算法，该算法将投影误差范数通过指数函数的映射直接得到平滑因子，实现更为简单。因此，为了提高NLMS-OCF[7]算法的性能，需要对步长进行控制，本文通过对NLMS-OCF算法迭代步长的研究，提出了一种变步长的NLMS-OCF(Variable Step-size Normalized Least Mean Square Algorithm With Orthogonal Correction Factors, VS-NLMSOCF)算法。

在本文中，将采取下列符号记法：||. ||表示欧几里得向量范数，(.)T表示一个矩阵或者一个向量的转置。标量是用小写字母或者大写字母表示，所有的向量都是列向量并用小写黑体字母表示，矩阵是用粗体大写字母表示。

1 NLMS-OCF算法

图1 自适应系统辨识Fig. 1 Adaptive filter in the system identification mode

对于k=1,2,...M，重复步骤(6)-(9)

从步骤（3）和（8）中可以看出，NLMS-OCF算法是采用定步长的，利用定步长很难在收敛速度和失调之间进行均衡，为了解决这个问题，在下一节中，提出了VS-NLMSOCF算法。

2 VS-NLMS-OCF算法

文献[4]中提出的VS-APA算法采用变步长策略，可变步长为：

其中μmax∈(0,2)，C是一个正数，可被近似为1/SNR，SNR为信噪比，pk是投影误差向量的估计，当||pk||2的值越大时，μk越接近于μmax，反之μk越接近于 0，即μk介于 0 与μmax之间。

当延迟因子设置为1时，APA和NLMS-OCF算法的权值更新是相同的[7]，因此，这种变步长策略同样适用于NLMSOCF算法，但是VS-APA算法采用固定的平滑因子，很难在收敛速度和失调之间进行均衡，本文通过对NLMS-OCF算法的研究，提出了一种变步长的NLMS-OCF算法，即用投影权值误差向量的范数通过指数函数的映射得到恰当的平滑因子，该算法实现简单，平滑因子α和||pk||2的关系如下：

其中，αk表示第k次迭代的α值，exp(.)代表指数函数。αk介于0和1之间，当||pk||2越大，αk越接近于0，反之，αk越接近于1。因此，这种指数更新策略满足算法对平滑因子的要求。

因此，将基于指数型平滑因子的变步长思想应用到NLMS-OCF算法中，其中（3）式可改为：

（8）式可改为：

相应地，（10）式可改为：

3 仿真结果

本部分，在MATLAB中分别将NLMS-OCF算法和VSNLMS-OCF算法进行了仿真比较，分析了两者的仿真结果。这两种算法的仿真结果的均方误差学习曲线是通过对100个相互独立的学习曲线求平均值而得到的。其中，维数N=32，μmax=1，p0=IN×1。

示例1：考虑表达式为xn=-0.95xn-1-0.6xn-2+zn的高度相关的输入信号模型，其中zn为均值等于0的高斯白噪声信号，正交校正因子M=2。从图2中可以看出，相比较于NLMSOCF算法（步长分别设置为0.1、0.5、1），VS-NLMS-OCF算法表现出了比较好的收敛速度和稳态误差。从图3中可以看出，常数C值的变化（当C分别设置为0.000 1、0.000 5、0.000 01）对VS-NLMS-OCF算法的收敛速度影响不是很大，其中，C的变化为一个数量级。

图2 均方误差学习曲线比较Fig. 2 Leaning curve of mean square error

图3 均方误差学习曲线比较Fig. 3 Leaning curve of mean square error

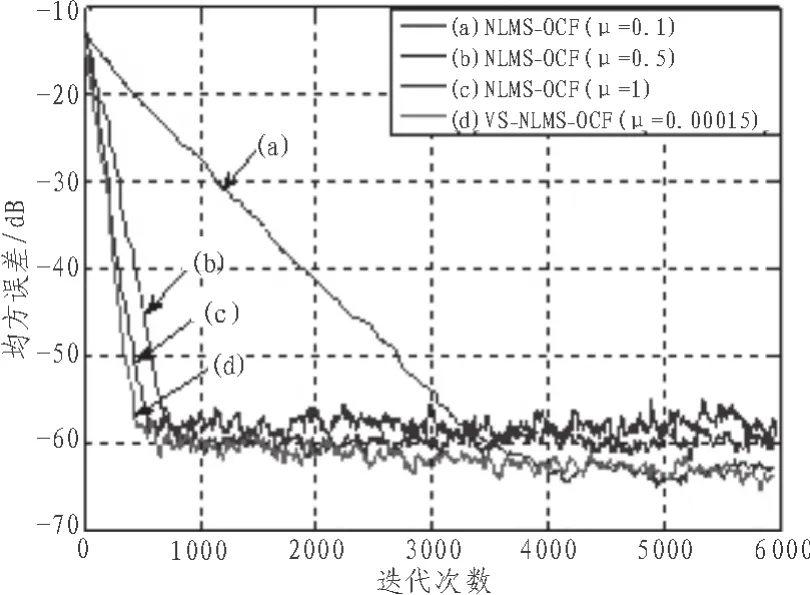
图4 均方误差学习曲线比较Fig. 4 Leaning curve of mean square error

示例2：考虑表达式为xn=-0.95xn-1-0.6xn-2-0.3xn-3+zn的高度相关的输入信号模型，其中zn为均值等于0的高斯白噪声信号，正交校正因子M=3。从图4中可以看出，相比较于NLMS-OCF算法，建立的算法获得了较好的收敛速度和稳态性能。

4 结 论

针对NLMS-OCF算法中的定步长问题，文中提出了变步长的NLMS-OCF算法，用投影权值误差向量的范数通过指数函数的映射得到平滑因子，其与定步长的NLMS-OCF算法相比，改进的算法具有更快的收敛速度和更小的稳态误差，提高了自适应滤波器的滤波性能。

[1]WidrowB,Stears S D.Adaptive Signal Processing [M].Englewood Cliffs, NJ:Prentice-Hall,1985.

[2]Haykin S.Adaptive Filter Theory [M].4th ed. Upper Saddle River,NJ:Prentice-Hall,2002.

[3]Mader A.Puder H,Schmidt G U.Step-size control for acoustic echo cancellation filters—An Overview"[J].Signal Process.,2000(80):1697-1719.

[4]Shin H.C., Sayed A.H.,Song, W J.,Variable step-size NLMS and affine projection algorithms" [J].IEEE Signal Process.Lett,2004,11(2):132-135.

[5]Dai, T., and Shahrrava, B.,Variable step-size NLMS and affine projection algorithms with variable smoothing factor[J].IEEE 48th Midwest Symp. Circuits and Systems, 2005(2):1530-1532.

[6]FanY,Zhang J,Variable step-size affine projection algorithm with exponential smoothing factors[J].The Institution of Engineering and Technology,2009:911-913.

[7]Sankaran S G,A A. (Louis) Beex,Fast Generalized Affine Projection Algorithm[J].International Journal of Adaptive Control and Signal Processing, February,2000,14(6):623-641.

Research on a variable step-size Normalized Least Mean Square algorithm with orthogonal correction factors

LI Ru, ZHANG Jun, ZHI Yong-feng
（Department of Automatic Control,Northwestern Polytechnical University,Xi'an710072,China）

To improve the performance of the adaptive filters, this paper presents a variable step-size normalized least mean square algorithm with orthogonal correction factors, which uses an exponential function to obtain proper smoothing factors from the projected error norm. Simulation results show that the proposed algorithm is superior in terms of convergence rate and estimation error compared with traditional NLMS-OCF algorithm.

adaptive filters; NLMS-OCF algorithm;variable step-size; convergence rate;estimation error

TN713

A

1674-6236(2014)07-0132-03

2013-08-01稿件编号201308020

国家自然科学基金资助项目(61201321)

李 茹(1987—)，女，河北石家庄人，硕士研究生。研究方向：数字通信与信号处理。