基于GM(1,1)模型的客运交通量预测系统实现
高云霞,高景刚,王植平,李清华,邱彦章,程鸿亮
(长安大学 电控学院,陕西 西安 710064)
基于GM(1,1)模型的客运交通量预测系统实现
高云霞,高景刚,王植平,李清华,邱彦章,程鸿亮
(长安大学 电控学院,陕西 西安 710064)
在对灰色系统理论研究的基础上,设计实现了一个基于GM(1,1)模型算法的预测系统,系统设计有友好的人机交互界面,包含数据库输入,数据预测、残差分析和拟合曲线五个子模块构成。通过对客运交通量实例数据仿真,证明了此预测系统精度较高,且该预测系统具有良好的通用性,可作为其他领域有关灰色预测设计的参考。
客运交通量;GM(1,1)模型;灰色预测;灰色系统理论;数据仿真
对客运量的可靠预测是部署和调整交通运输发展战略规划的重要依据,是舒缓交通压力和保证交通运输畅通的有效手段。但交通客运量受诸多因素影响,具有很大的随机性和灰色特征,这无疑给交通预测工作带来了困难。目前国内外的研究人员已经在交通预测方面做了大量的工作[1-4],并提出了一些预测方法。例如指数平滑法、回归分析法、人工神经网络法等。这些方法在实际应用中效果良好,但也有其缺点:这些方法都必须收集大量信息,由此带来的问题是建模困难,计算工作量大。有时既使模型能够建立,也往往因缺少足够的信息而不能确定具体的模型参数,从而导致无法实现预测[1]。而灰色预测方法避开了这些复杂关系,它着眼于系统本身的灰色信息,即寻找系统的内在规律,达到使灰色白化的目的,采用灰色系统理论中GM(1,1)模型实现客运交通量预测系统是可行的。
1 GM(1,1)模型的建模过程
灰色系统的基本观点是一切随机量都看作是在一定范围内变化的灰色量,对它的处置不是找概率分布、求统计规律,而是将原始列数据按一定要求作数据处理,来找数据间的规律。对系统的行为特征数据进行生成,就是企图从杂乱无章的表面现象中去发现潜在规律。其预测算法GM(1,1)的建模过程如下:
设有n个变量,每个变量有非负的N个数据列,并设xi为系统主行为,则:




2)残差修正:建模后要检验模型是否合适,残差检验就是得到模型后检验绝对残差与相对残差是否满足要求,如不满足就要进行残差修正处理: 记k时刻残差为q(k):
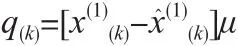

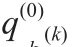

按灰色建模的残差数列则同样可建立白化形式的GM(1,1)残差动态模型:

可以说,残差识别是灰色建模理论独特而精彩的处理方式。
3)还原计算:再经过一次累减还原和初值化还原,即可得到待求的预测值:
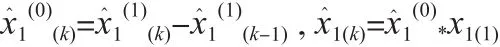
2 GM(1,1)在全国旅客周转交通量预测中的应用
设计希望在应用GM(1,1)灰色模型预测算法基础上完整实现对数据的处理功能,即调入已知交通客流量数据,利用算法对数据进行预测,并对所预测出的数据进行误差处理以及最后的曲线对比输出,从而完成对整个交通流量的预测,设计模块如下:
1)数据调入:在工程中通常用EXCEL软件保存所要处理的数据。鉴于此,交互界面设计了文件选择功能,操作者可按照所存储的数据路径找到所需预测的数据,随后即可在界面中看到将被处理的数据。
2)数据预测:该功能是界面设计的核心,即完成对灰色预测模型GM(1,1)的嵌入。功能是在完成功能(1)调入数据的处理后,实现预测处理并给出预测结果。
3)误差处理:这一功能的设计用来说明预测结果的合理性,具体用到的是残差检验法,通过生成曲线,让用户准确地看到预测数据与原始数据间误差的大小。
4)输出对比曲线:为给用户直观的认识,界面中设计了曲线的对比输出。操作者可以看到预测数据与原始数据间的差异,通过比较两条曲线走势,用户就可对预测结果做出合理的取舍。
图1是利用GM(1,1)算法进行客运交通量预测的设计流程,其中“数据调入”,是从系统硬盘中选取以“EXCEL”文件保存的数据;“数据预测”是整个设计核心,其界面设计如图2所示;“误差处理”是计算预测值与原始值之间的相对误差,而“对比曲线输出”则可辅助用户比较预测数据与原始数据之间的差异。

图1 客运交通量预测流程图Fig. 1 Forecasting flow chart of the passenger traffic volume

图2 客运交通量界面Fig. 2 Passenger traffic interface
理论上说,任何预测对象,只要能抽象出表征系统特征的时间序列,就可用该灰色模型进行预测,所设计的交互界面也可作为其他领域的灰色预测设计参考。经过对模型算法的改进及对预测功能的丰富,可以集成一款较理想的预测软件,普及灰色系统理论在解决含未知因素的特殊领域的问题时应用。
2.1 仿真结果
在对客运交通量预测子系统界面的仿真中,所选用的数据来自中国国家统计局(http://www.stats.gov.cn)1992-2002年每年全国的旅客周转量,具体仿真过程如下图3所示,图3中(a)、(c)为仿真结果,(b)图为所调入的EXCEL数据文件。在单击界面中的“调入”按钮后,就可以在系统硬盘中寻找所需要的数据文件,然后双击文件就可以将数据导入到预测界面中的“Edit Text”图形对象中,如图(c)所示。接着,在单击“误差”按钮和“对比曲线”按钮后,就可得到如图(c)所示的结果。其中,左侧“Edit Text”图形对象中所显示的是误差结果,单位是“%”,而右侧“Axes”图形对象输出的是预测数据与原始数据间的曲线。
2.2 预测数据误差处理及结果分析
汇总仿真界面的所有数据如表1所示,可知利用GM(1,1)灰色预测模型对1992~2002年的全国旅客周转量的预测误差比较小,最大误差约为4.09%,这是由于1997~1998年原始
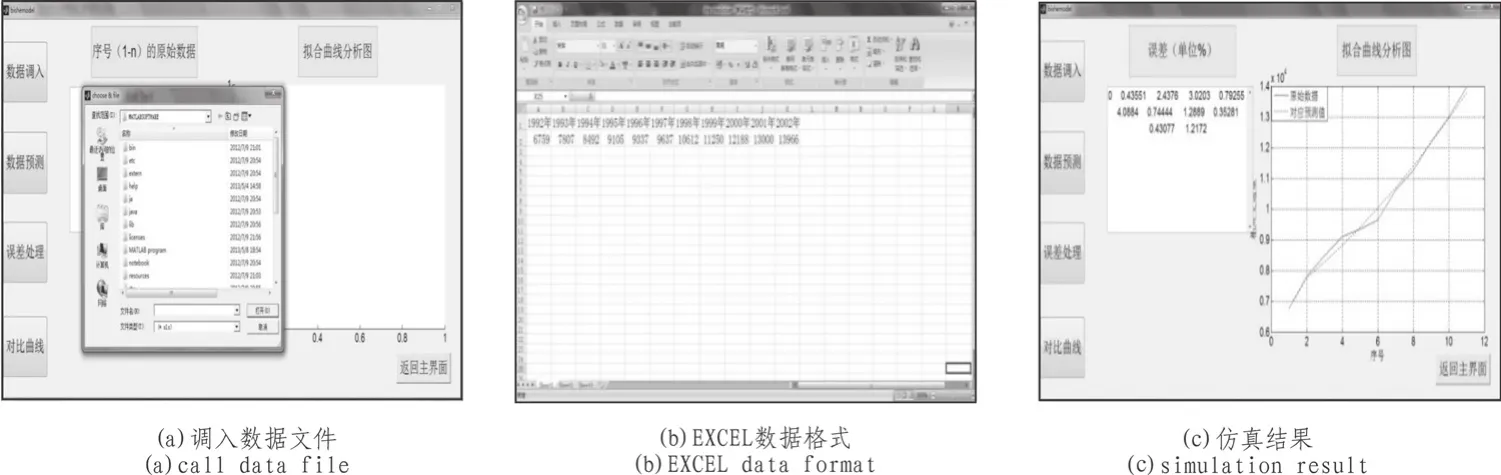
图3 交通量预测的仿真结果Fig. 3 Simulation result of the traffic volume forecast
表1 1992~2002全国客运量交通预测数据(亿人/Km)分析表
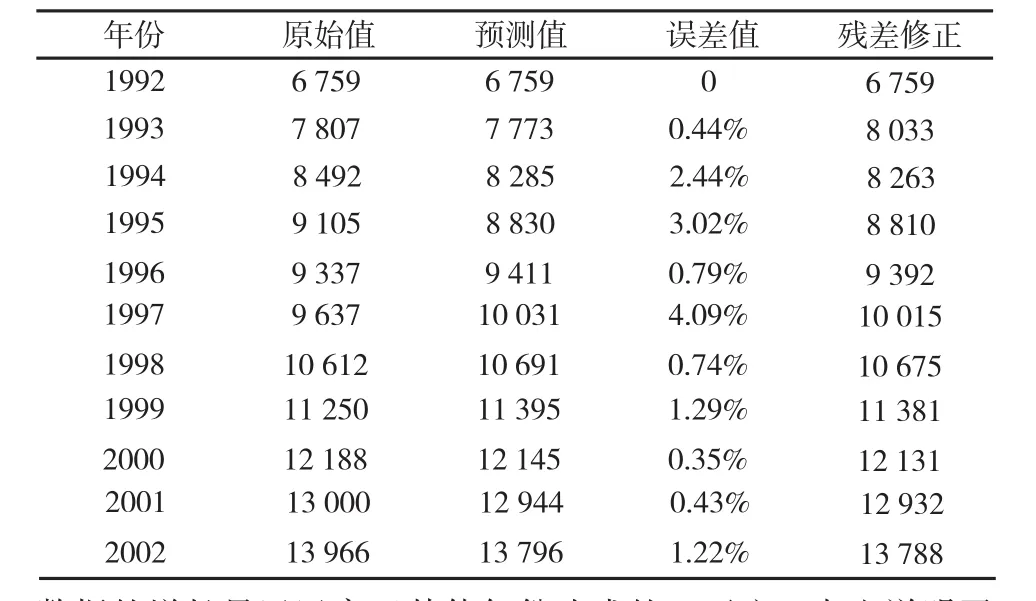
年份 原始值 预测值 误差值 残差修正1992 1993 0 1994 1995 6 759 7 807 8 492 9 105 6 759 7 773 8 285 8 830 0.44%2.44%3.02%6 759 8 033 8 263 8 810 19969 3379 4110.79%9 392 19979 63710 0314.09%10 015 199810 61210 6910.74%10 675 199911 25011 3951.29%11 381 12 131 12 932 13 788 2000 2001 2002 12 188 13 000 13 966 12 145 12 944 13 796 0.35%0.43%1.22%
Tab.1 Forecast data analysis table of the national passenger traff i c (one hundred million/Km) in 1992~2002数据的增长量远远高于其他年份造成的,而这一点也说明了GM(1,1)模型的缺点,即要求原始数据要“规矩”,其增长趋势要稳定一致。但由于误差在5%范围内,联系实际可知,预测所得到的发展趋势与我国交通业的实际发展情况非常相近。
3 结束语
利用GM(1,1)模型算法,以建立预测模型为基础,设计实现了客运交通量的预测应用系统;通过残差修正改进预测精度(小于5%),较理想地完成了对客运交通量的预测。为方便管理人员操作,设计了简单友好的人机交互界面和子界面,实验证明具有良好的稳定性和可靠性。
基于交通客运量影响因素的复杂性,没有任何一种预测模型是万能的,每一种模型都有其亮点特色和应用条件,故后期工作可建设客运交通量预测系统的数据库,丰富完善该预测系统;同时可把其他预测模型整合起来,建设综合互补型的客运交通量预测系统,以适应客运交通量预测的复杂多边性。使之能应用于城市交通的管理和决策,辅助对城市进行智能化管理。
[1]吴伟,符卓,王晓,运输通道客运量预测方法[J].铁道科学与工程学报,2012,6(5):97-102.
WU Wei,FU zhuo,WANG xiao.Passenger volune forecast method for transport corridor[J].Journal of Railway Science And Engineering, 2012,6(5):97-102.
[2]花丙威,基于灰色理论的水路客运预测方法研究[J].湖南交通科技,2012,38(3):139-146.
HUAN bing-wei,The forecast method research of Waterway passenger transport based on the gray theory[J].Hunan Communication Science And Technology ,2012,38(3):139-146.
[3]Salgado R M,Ohishi. A Hybrid Ensemble Model Applied to the Short2Term Load Forecasting Problem[J].Neural Networks,2006,IJCNN.06 International Joint Conference 2006(7):2627-2634.
[4]江志华,朱国宝.灰色预测模型GM(1,1)及其在交通运量预测中的应用[J].武汉理工大学学报,2003,28(2):305-307.
JIANG hua,ZHU Guo-bao.Grey Model-GM(1,1)And Its Application to Predicting Transportation Volume[J].Journal of Wuhan University of Technology:Transportation Science and Engineering, 2003,28(2):305-307.
[5]王生昌,白韶波,张慧.公路客运量预测方法比较[J].长安大学学报:自然科学版,2005,25(5):1-3.
WANG shen-chang,BAI shao-bo,ZHANG hui.Prediction methods of highway passenger volume[J].Journal of Chang’an University :Natural Science Edition,2005,25(5):1-3.
[6]侯丽敏,马国峰.基于灰色线性回归组合模型铁路客运量预测[J].计算机仿真,2011,28(7):83-85.
HOU li-min,MA guo-feng.Forecast of Grey Linear Regression Combined Model[J].Computer Simulation, 2011,28(7):83-85.
[7]李秋月.灰色预测模型的应用研究[J].数学的实践与认识,2013,43(11):90-95.
LI qiu-yue.The Application Research of Grey Forecasting Model[J].Mathematics in Practice And Theory,2013,43(11):90-95.
The passenger traff i c volume prediction system of GM (1, 1) model algorithm
GAO Yun-xia, GAO Jing-gang, WANG Zhi-ping, LI Qing-hua,QIU Yan-zhang, CHENG Hong-liang
(School of electronics and control,Chang'an University,Xi'an710064,China)
The passenger traffic volume forecasting system was designed which based on the GM(1,1) algorithm. The System had friendly man-machine interface, and contained five sub modules :the database input, data prediction, the residual analysis and curve fitting. Through the simulation of passenger traffic volume instance data, it proved that the prediction system was high precision. Moreover, the prediction system had good commonality, which could be taken as the reference to other areas of grey forecasting design.
passenger traffic volume; GM (1, 1) grey model; grey forecasting; grey system theory; simulation data
U125
A
1674-6236(2014)07-0016-03
2013-08-02稿件编号201308029
中央高校基本科研专项基金(CHD2010JC128)
高云霞(1975—),女,陕西西安人,硕士,讲师。研究方向:微机应用技术。

