基于全程滑模变结构控制的有源电力滤波器

刘国海，张琛，陈兆岭，钱鞠，沈跃

（1.江苏大学电气信息工程学院，江苏镇江212013；2.江苏省中森建筑设计有限公司，江苏镇江212013）

1 引言

随着非线性负荷的大量应用，电网中的谐波问题越来越严重。有源电力滤波器能对频率和幅值变化的谐波进行实时补偿，在电能质量领域受到广泛重视［1］。

APF的电流控制方法很多，主要有滞环比较控制、三角载波控制、无差拍控制以及电压空间矢量控制等［2］。为提高APF 控制性能的鲁棒性，对参数摄动及外界干扰等不确定因素具有不变性的滑模变结构控制方法被应用于APF中，取得了一些研究成果［3-10］。但这些方法也存在不足：只有当系统处于滑动模态阶段时，才具有对参数摄动和外界干扰的不灵敏性，而在趋近阶段则不具有鲁棒性［11］。

本文提出一种基于全程滑模变结构控制方法的APF 控制策略，将GSMVSC 应用于APF 的电流跟踪控制中。设计的控制律将系统状态始终保持在切换平面上，消除了趋近阶段，改善了系统的瞬态性能，克服了未知参数摄动的影响。应用Matlab软件对基于GSMVSC 的APF 进行仿真，结果表明本方法可行，增强了系统的鲁棒性。

2 APF数学模型

图1 为三相3 线并联型APF 的系统结构图。由功率开关S1～S6构成的三相电压源型PWM 逆变器产生三相补偿电流ica，icb，icc，和三相负载电流iLa，iLb，iLc相加后，将三相电源电流isa，isb，isc补偿成正弦电流。

图1 三相3线并联型APF系统原理图Fig.1 Circuit diagram of three-phase three-wire shunt APF

图1中，Lc和Rc为APF 注入电感和及其等效电阻，C 为APF 直流侧电容，LL和RL为整流装置的负载。

以N点为参考电位，可列出方程如下：

其中，d1，d2，d3分别为3个桥臂的开关函数，di=1表示i 桥臂上管导通、下管关断；di=0 表示i 桥臂上管关断、下管导通。由于usa+usb+usc=0，ica+icb+icc=0，将式（1）中3式相加，得：

将式（2）代入式（1），整理得：

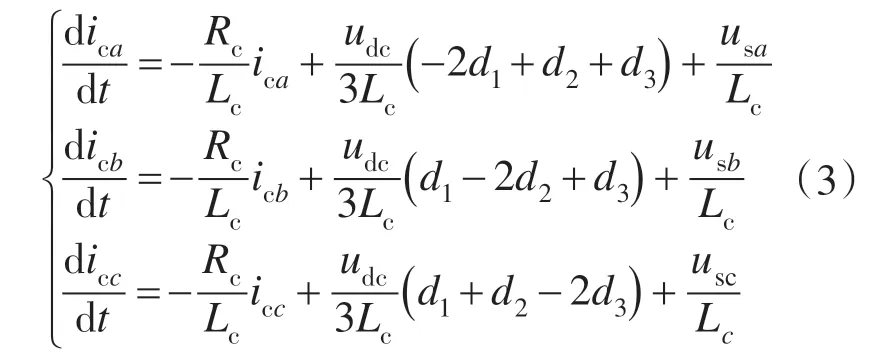
上式可写成矩阵形式：

其中i=［ica，icb，icc］Tu=［d1，d2，d3］T

3 滑模变结构控制系统设计

3.1 全程滑模变结构控制器设计

全程滑模变结构控制APF的目标是：使有源电力滤波器的输出电流等于谐波检测算法所计算出的指令电流。这实际上是一个给定运动的跟踪问题［12］。引入偏差变量xi=ici-ici*，i=a，b，c。

全程滑模变结构控制器设计中利用abc坐标系下的误差分量Δica，Δicb，Δicc构造滑模面，定义控制律ua，ub，uc，再经过符号判断得到新的控制律最后，构造驱动开关管的PWM 信号ds1～ds6。如图2所示。

图2 全程滑模变结构控制系统设计Fig.2 General block diagram of GSMVSC control strategy

3.2 滑模函数和控制律设计

定义滑模切换函数为

式中：C为滑动模态参数矩阵；E（t）=diag［exp（-βat），exp（-βbt），exp（-βct）］，i=a，b，c，Re（βi）>0，βi为滑动模态移动参数。

根据系统设计指标，采用滑动模态的极点配置法得到系统期望极点集为{p}，则滑动模态移动参数为

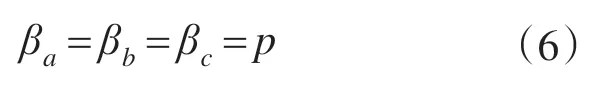
滑态参数阵为

式中：Ⅰ3为单位阵；T 为非奇异线性变换矩阵，它是由能控判别矩阵U=［B┊AB┊A2B］的3个线性无关的列所组成。

由于系统状态一开始就处于所设计的切换平面上，因此变结构控制律的设计任务是将系统状态可靠地保持在滑动模态上。构造以下变结构控制律：

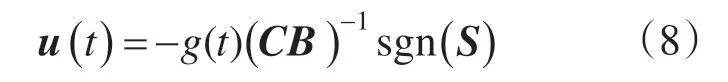
式中：g（t）为待确定的变结构控制系数，g（t）>0；sgn（S）为符号函数。

3.3 稳定性分析

选取Lyapunov 函数V（S），所设计的滑动模态可达条件为

将式（9）代入可得：

其中

结合式（8）、式（9）和式（10），利用数学推导有：

其中||·||对矩阵而言是2阶诱导范数，上式可写成：

式中：ε为一小正数，可保证V˙(S)＜0。

其余系数为

为了消除高频振颤现象，采用消颤方法，即用下式来代替式（9）中的sgn（S）

式中：δi为一个小的正常数。

4 仿真结果及其分析

模拟电网系统，利用上述数学模型和控制理论，在Matlab/Simulink环境下建立有源电力滤波器及其控制系统。其中，阻感负载RL=14 Ω，LL=64.5 mH，主电路输入电阻电感Rc=0.2 Ω，Lc=2 mH，直流侧电容C=663.3µF，udc=800 V。假设控制开始时，三相电流ica，icb和icc均存在小的偏差量，即系统初始状态为

我们希望通过调节使得偏差为0，实现补偿电流准确跟踪指令信号。所设计的干扰量为5sin（2t）。这里为计算方便，滑动模态运动的希望极点集元素根据公式估算取经验值βi=3，滑动模态参数矩阵为

无外界扰动时，分别采用定常滑模变结构控制和全程滑模变结构控制方法，在0.03 s 时刻将APF投入电网补偿前后a相电源电流isa波形如图3所示。可以看出：两种控制方法都对电网电流进行了实时补偿，但全程滑模变结构控制补偿效果要优于定常滑模控制。同时，采用定常滑模控制需要经过一段时间，大约经过0.1 s才能趋于稳定，即存在趋近阶段，而采用全程滑模变结构控制方法则使系统状态点在APF投入运行初始状态时就落在滑模面上，从而避免了系统在趋近阶段对扰动的灵敏性。

图3 无外界扰动时两种控制方法补偿后电网侧a相电流波形Fig.3 The a-phase current waveforms after compensation without exogenous disturbance using two methods

当电网负载在0.2 s时突变为原值的一半，同时将Rc，Lc变化±5%后，APF分别采用定常滑模变结构控制和全程滑模变结构两种控制方法补偿后电网侧a相电流波形isa如图4所示。可见全程滑模控制方法对元件参数变化和负载变化具有强鲁棒性，且动态性能更好。

图4 两种控制方法在元件参数变化和负载变化时补偿后电网a相电流波形Fig.4 The a-phase current waveforms after compensation with self-parameters perturbation and load change using two methods

图5反映的是当系统加入正弦干扰5sin（2t）后，APF 分别采用定常滑模变结构控制和全程滑模变结构控制方法补偿后a相网侧电流isa波形对比。

图5 两种控制方法在扰动存在时补偿后电网侧a相电流波形Fig.5 The a-phase current waveforms after compensation with exogenous disturbance using two methods

采用定常滑模控制方法时，isa的总谐波畸变率（THD）可达到16.71%，而采用全程滑模控制方法时isa的THD 只有2.36%，由此可见全程滑模控制对外界干扰具有强鲁棒性。

5 结论

本文提出了一种基于全程滑模变结构控制的APF 控制策略。在对APF 状态空间描述的基础上，设计了全程滑模变结构控制方法。对定常滑模控制方法和全程滑模控制方法在APF 的应用进行了对比仿真，结果表明采用全程滑模控制方法具有更强的抗元件参数变化和抗外界干扰能力，鲁棒性强，同时响应快速。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.第2版.北京：机械工业出版社，2005.

［2］王晓刚，谢运祥，帅定新.智能控制方法应用于APF的综述与展望［J］.电网技术，2008，32（8）：35-41.

［3］陈兆岭，孙京京，刘国海，等.基于积分变结构控制的并联型有源电力滤波器研究［J］. 电测与仪表，2012，49（10）：55-59.

［4］Mendalek N，Al-Haddad K，Hassoun G，et al. Sliding Mode Control of Three-phase Four-leg Shunt Active Power Filter［C］// Power Electronics Specialist Conference. IEEE，2008：4362-4367.

［5］Mendalek N，Al-Haddad K，Fnaiech F，et al. Sliding Mode Control of 3-phase Shunt Active Power Filter in the d-q Frame［C］// Power Electronics Specialist Conference. IEEE，2002：369-375.

［6］周为平，吴正国，刘大明，等.有源电力滤波器变趋近律滑模变结构控制［J］. 中国电机工程学报，2005，25（23）：91-94.

［7］王婷婷.有源电力滤波器的滑模变结构控制［J］.电气传动自动化，2011，33（5）：18-21.

［8］张晓，孔令军，孙华，等.三相三线制并联型有源电力滤波器的准滑模变结构控制［J］.电力系统保护与控制，2011，39（21）：40-44.

［9］陶以彬，杨苹，钟国基.基于滑模变结构控制的有源电力滤波器研究［J］. 电力电容器与无功补偿，2008，29（5）：18-22.

［10］郭伟峰，武健，徐殿国，等.新型滑模控制的并联混合有源电力滤波器［J］.中国电机工程学报，2009，29（27）：29-35.

［11］樊丁，赵庆荣. 航空发动机全程滑态变结构控制研究［J］.推进技术，2002，6（23）：485-488.

［12］胡强晖，胡勤丰. 全局滑模控制在永磁同步电机位置伺服中的应用［J］. 中国电机工程学报. 2011，31（18）：61-66.