一种适用于频率变化的单相数字锁相环

周敏杰，史旺旺

（扬州大学水利与能源动力工程学院，江苏扬州225009）

1 引言

随着环境问题和能源需求的增加，风能和太阳能等新能源发电技术得到了广泛的应用。与此同时单相并网发电系统的运行性能要求也在逐渐提高。在新能源单相并网发电系统中，电网电压的相位、幅值和频率是并网运行的关键信息。电网电压相位和频率的准确获得直接影响着单相并网系统的稳态、动态性能及其安全运行［1-3］。目前单相系统中数字锁相环技术在跟踪获取电网电压相位和频率方面得到了广泛应用。

在单相系统中，传统数字锁相环采用过零鉴相的方法，它是通过检测电网电压过零点来得到相位信息。该方法虽然实现简单，但是在2 个检测点之间如果频率发生变化时，则不能实现快速跟踪相位变化，抗干扰能力差，锁相效果差。另外还有虚拟乘法器鉴相和构造虚拟两相法鉴相等鉴相方法。其中虚拟乘法器的不足之处在于若输入信号中存在2 倍频信号，采用一般的低通滤波器时，滤波器的惯性时间常数必须取较大的数值，这就会影响系统的响应速度。另一方面，当电网电压信号存在高次谐波时，输入信号存在高次谐波分量，一般的滤波器很难滤除所有的谐波分量［4-10］。根据构造方法的不同，构造虚拟两相法鉴相可分为延时法构造虚拟两相、微分法构造虚拟两相等鉴相方法［11-14］。延时法构造虚拟两相需要通过将电网电压延时90°以获得虚拟信号，来构造两相正交信号。延时90°相位角是通过延时T/4 周期来实现的，要能够准确实现正弦信号延时90°的前提是已知正弦信号的周期或频率，而锁相环控制的目的就是跟踪未知的输入频率，当电网电压频率发生变化时，延时T/4存在误差，因而延时相位角也存在误差。

当电网频率是50 Hz 时，通过延时法构造虚拟两相电压矢量在平面中的轨迹是一个圆。电网频率发生变化时，构造的虚拟两相电压矢量在平面中的轨迹是一个椭圆，本文提出了椭圆拟合［15-17］的数字锁相环方法。它利用递推最小二乘法椭圆拟合方法获得椭圆的参数，再由锁相环产生不对称的正、余弦输出，使得电网频率发生变化时鉴相器输出的2 倍频分量被消除。本文推导了不对称相位和椭圆参数的关系，设计了带遗忘因子的递推最小二乘法，最后给出了实验结果。

2 单相频率变化时的椭圆方程

单相系统中，通过延时法产生与电网电压信号相差90°的电压信号，来构成两相正交的静止坐标系αβ，得到电压信号的正弦、余弦分量。正弦、余弦分量表达式为

式中：U为电网电压幅值；θ0，ω0，φ0分别为αβ坐标系下电网电压的相位角、角频率和初相位。

当频率为50 Hz时，电压信号的正弦分量Uα、余弦分量Uβ在平面上的轨迹为圆。当频率发生变化时Uα，Uβ在平面上的轨迹为一个椭圆，此时电压方程为

式中：x为α轴分量；y为β轴分量；φ为相位不对称程度。

将式（2）中的时间t消除后就得到椭圆方程：

令

则得到如下椭圆方程：

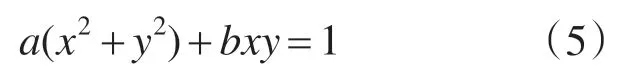
由式（4）可得：

当通过辨识获得椭圆参数a，b后，由式（6）求得φ和U。

3 递推最小二乘法椭圆拟合

比较常用的椭圆曲线拟合方法主要有以下3种：第1种是基于不变矩的椭圆拟合方法；第2种方法是基于HOUGH 变换的拟合方法；第3 种是基于最小二乘法的椭圆拟合方法。在这几种拟合方法中，最小二乘法椭圆拟合适用于各种复杂的对象模型，它能使得测量误差的平方和最小，可以直观地给出关于某种拟合误差的测度，能够达到很高的精度。因此，最小二乘法椭圆拟合方法被认为是一种从一组测量值中求出一组未知量的可信赖的方法。由于本文中椭圆方程有2个未知数，测量点数m需大于等于2。设m个测量点为xi，yi，满足式（5），用矩阵表示为

其中

随着观测数据的增多，将增加计算量和加大计算的困难度，并且随着计算次数的增加会出现“数据饱和”现象，参数估计值和参数的真值之间的误差会越来越大，将导致参数估计值不能跟踪时变参数的变化。为了能够动态跟踪时变的椭圆参数，减少实时计算工作量，本文采用了带遗忘因子的递推最小二乘法。定义为

其中

式中：α为遗忘因子。

则可得椭圆参数递推公式为

遗忘因子大小的选择对椭圆参数算法的跟踪性能和收敛速度有着很大影响。其值越大，则对时变参数的跟踪能力减弱，但对噪声不敏感，椭圆参数的估计误差越小；其值越小，则对椭圆参数的跟踪能力越强，响应越快，但同时对噪声越敏感。因此，只有当遗忘因子有准确的取值时，才能确保对时变参数的快速跟踪能力和较小的参数估计误差。

4 不对称相位输出锁相环

锁相环中鉴相器的作用是相位比较，把输出信号和输入参考信号的相位进行比较，产生2个信号的相位差，当频率变化时锁相环鉴相输出中存在2 倍频分量，影响着锁相环的性能。若能够准确地辨识出静止坐标系下故障电压的相位差，采用不对称输出锁相环，就可以将2 倍频分量消除。

设锁相环α轴的输出分量为x1，β轴的输出分量为y1，可得：

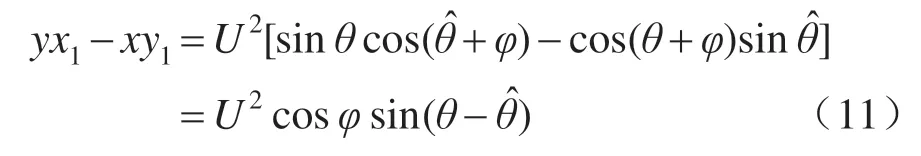
式中：θ为锁相环输入信号相位，θ=ω0t+φ0。

从式（11）中可看出，当椭圆拟合准确时鉴相器输出无2 倍频分量，椭圆拟合的锁相环框图如图1所示。

图1 基于椭圆拟合的锁相环框图Fig.1 Block diagram of DPLL based on ellipse fitting

5 仿真和实验结果

为验证所提出的控制方法的正确性，在上述理论分析的基础上，本文建立了如图1 所示的系统结构，并使用Matlab对单相数字锁相环进行了仿真测试。图2 是锁相环输入输出电压波形，其中x为输入波形，x1为输出波形。图2中可看出数字锁相环在1个电网周期内就可实现对输入信号的跟踪锁定，同时能够输出较光滑的电压波形，能起到较好的滤波效果。

图2 输入电压包含谐波时的仿真波形Fig.2 Simulation under the condition of voltage harmonics

不同频率下的电压轨迹图如图3 所示，图3a中显示在50 Hz下电压轨迹为一圆；图3b中显示在60 Hz下电压轨迹为一椭圆。为了测试电压频率突变时的相位跟踪能力，在0.1 s时输入电压信号的频率从50 Hz突变为60 Hz，频率突变时的锁相环输出波形如图4 所示，可以看出频率变化时数字锁相环仍可以迅速地跟踪锁定相位。

图3 50 Hz和60 Hz频率时的电压轨迹图Fig.3 Path of input voltage with frequency of 50 Hz and 60 Hz

图4 频率突变时的电压波形Fig.4 Voltage with frequency mutation

为验证电压相位突变时锁相环的性能，电压相位提前π/4，此时锁相环输出电压波形如图5所示，锁相环可以迅速锁定相位，具有较好的相位跟踪的动态性能。

图5 相位突变时的电压波形Fig.5 Voltage with phase mutation

为了验证电网故障时锁相环的控制效果，进行了实验测试。实验系统平台采用TI 公司的F28335DSP芯片，当电网电压故障时实测的电压波形和锁相环输出的电压波形如图6所示。锁相环能在1 个周期内锁定电压相位，并且能够消除实际采样中产生的谐波干扰。

图6 实际采样时的输入电压曲线和锁相环输出曲线Fig.6 Input and output curves from sampling data

6 结论

本文提出了一种新型的数字锁相环。针对在两相静止坐标系中，电网电压频率变化时电压在平面上的轨迹为一椭圆，提出用带遗忘因子的递推最小二乘法来获得椭圆拟合参数，使锁相环输出不对称相位来消除电网电压频率变化时存在的2 倍频分量，进而达到快速跟踪锁定相位的目的，同时也较好地滤除了故障时输入电压的谐波。从仿真和实验的波形中可看出所设计的新型数字锁相环具有良好的稳定性和动态特性。通过对锁相环仿真结果和实验结果的深入分析，本文所提出的基于椭圆拟合的数字锁相环方法是正确和可行的，适用于单相系统的应用场合。

［1］李明，王跃，方雄，等.无正交虚拟信号生成的单相DQ锁相环研究［J］.中国电机工程学报，2011，31（15）：27-32.

［2］刘进军，刘波，王兆安.基于瞬时无功功率理论的串联混合型单相电力有源滤波器［J］.中国电机工程学报，1997，17（1）：37-41.

［3］庞浩，俎云霄，王赞基.一种新型的全数字锁相环［J］.中国电机工程学报，2003，23（2）：37-41.

［4］任碧莹，钟彦儒，孙向东，等.基于有限冲击响应滤波器线性相移控制的单相系统数字锁相环［J］. 电工技术学报，2008，23（8）：121-125.

［5］Suul J A，Ljokelsoy K，Undeland T.Design，Tuning and Testing of a Flexible PLL for Grid Synchronization of Three-phase Power Converters［C］// EPE 2009. 13th European Conference，2009：1-10.

［6］Arruda L N，Silva S M，Filho B J C.PLL Structures for Utility Connected Systems［C］//Thirty-sixth IAS Annual Meeting，2001：2655-2660.

［7］Salamah A M，Finney S J，Williams B W.Three-phase Phaselock Loop for Distorted Utilities［J］. Electric Power Applications，IET，2007，1（6）：937-945.

［8］袁江伟，吕征宇.一种新型的单相并网系统锁相环［J］.电力电子技术，2011，45（7）：81-82，100.

［9］金曼，苏建徽.光伏并网逆变器中的单相数字锁相环研究［J］.电力电子技术，2011，45（6）：6-8.

［10］Naidu S R，Mascarenhas A W，Fernandes D A. A Software Phase Locked Loop for Unbalanced and Distorted Utility Conditions［C］// 2004 International Conference on Power System Technology，2004：999-1004.

［11］Sun Xiangdong，Zhang Qi，Biying Ren，et al. A Novel Digital Phase-locked Loop for Distributed Grid-connected Power Generation Systems under Unbalanced and Distorted Utility Conditions［C］//2010 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems，2010：813-817.

［12］吴春华，许富强，周笛青，等.一种单相锁相环的数字实现［J］.电气传动，2012，42（6）：13-16.

［13］王冲，於锋，陈荣.基于广义积分器的电力单相锁相环研究［J］.高压电器，2011，47（4）：13-16，22.

［14］陈自强，黄守道，曾智波，等.新型锁相技术在单相系统中的应用研究［J］.计算机仿真，2011，28（1）：315-318.

［15］闫蓓，王斌，李媛. 基于最小二乘法的椭圆拟合改进算法［J］.北京航空航天大学学报，2008，34（3）：295-298.

［16］吕洪赫，姚振杰，易卫东.基于对称性的最小二乘拟合随机椭圆检测法［J］.电子测量技术，2011，34（5）：37-41.

［17］邹益民，汪渤.一种基于最小二乘的不完整椭圆拟合算法［J］.仪器仪表学报，2006，27（7）：808-812.