PWM三相电流滞环解耦控制研究

张小青，樊战亭，张宣妮

（咸阳师范学院物理与电子工程学院，陕西咸阳712000）

1 引言

随着电力电子技术、开关电源、变频器等技术的发展，电流控制技术被提出了越来越高的要求。电流控制已是各种高性能功率变换器常用的核心技术之一，常常作为功率变换器控制系统的内环，其性能直接影响到功率变换器的控制性能［1-2］。电流滞环跟踪控制的交流变频器具有输出电流正弦度高，电流易于控制的优点［3］，其应用越来越广泛。对转速动态性能要求较高的三相异步电动机控制系统中，需要利用对称的三相3 线正弦交流电流来形成均匀稳定的旋转磁场［4］。对单相电流滞环跟踪技术已进行了大量的探讨研究［5-11］，其中文献［11］深入分析了三态准PWM电流滞环控制技术及其在异步电机中的应用，但未对三相3线制系统电流存在的耦合问题提出解决方案。目前三相3 线变换器电流解耦方案有很多，但多是针对有功电流和无功电流之间的解耦控制方案［12］，而电流滞环跟踪是一种非线性电流控制技术，仅需利用简单的叠加原理就可以实现解耦。本文就是这样利用电流滞环跟踪技术与叠加解耦原理来产生三相逆变器所需的PWM控制波，从而得到三相3线对称正弦交流电流，通过仿真比较验证了其有效性及优越性。

2 三相逆变器电路结构

三相逆变器电路结构如图1所示。三相交流电经三相桥式整流电路及电容滤波后变成了具有恒定电压值的直流电，为后面的三相桥式逆变器提供输入。为了保证三相桥式逆变器能快速开关，在这里采用了高频率的全控型MOS管，而MOS 管的门极触发信号由电流滞环跟踪及反馈解耦PWM波来控制。开关管VTb与Rb用来解决电路泵升电压问题，当控制器检测到泵升电压高压规定值时，开关管VTb导通，使多余的能量通过放电电阻Rb消耗掉。

图1 三相逆变电路结构图Fig.1 Structure diagram of 3-phase inverter

3 三相3 线电流耦合分析及解耦设计

3.1 三相3线电流耦合分析

当图1中的负载为三相对称负载时，有

记三相参考电流分别为irA，irB，irC，电流跟踪误差分别为ΔiA，ΔiB，ΔiC，则

定义Sa，Sb，Sc分别表示三相的开关状态，“1”表示上桥臂导通，“-1”表示下桥臂导通。当Sa=1 时，ua=0.5Udc；当Sa=-1 时，ua=-0.5Udc，即有ua=Sa·0.5Udc，b，c节点情况相类似。因而根据图1，可列方程如下：

其中

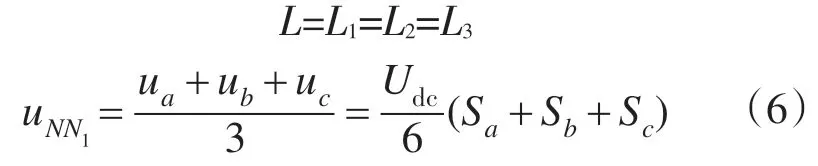
式中：uNN1为三相电压中性点N 与直流中性点N1之间的电压差。

从式（5）、式（6）明显看出A 相电流不仅与其对应的开关状态Sa有关，还与Sb，Sc有关，对于B，C相情况类似。为了能较好地控制各相电流，必需进行一定的解耦控制。

3.2 解耦设计

为了解除各相之间的耦合控制，先假设N 与N1点之间的压差为0。根据叠加原理，式（5）可分解两部分之和为

4 电感参数计算

电流跟踪型逆变器中电感的选取很重要，它不仅会影响逆变器的外特性［13］，而且会直接影响逆变器的跟随性及主电路开关元件的使用寿命［14］。在负载一定的情况下，电感是决定跟踪性能的关键因素。

设主电路开关元件的允许开关频率fc为20 kHz，参考电流频率f 为50 Hz，环宽H 设为0.1，参考电流的幅值Irm为2 A，直流电压Udc为20 V，计算电感的上、下限值［7］：

所以L取3 mH。

5 方案验证

5.1 解耦方案的实现

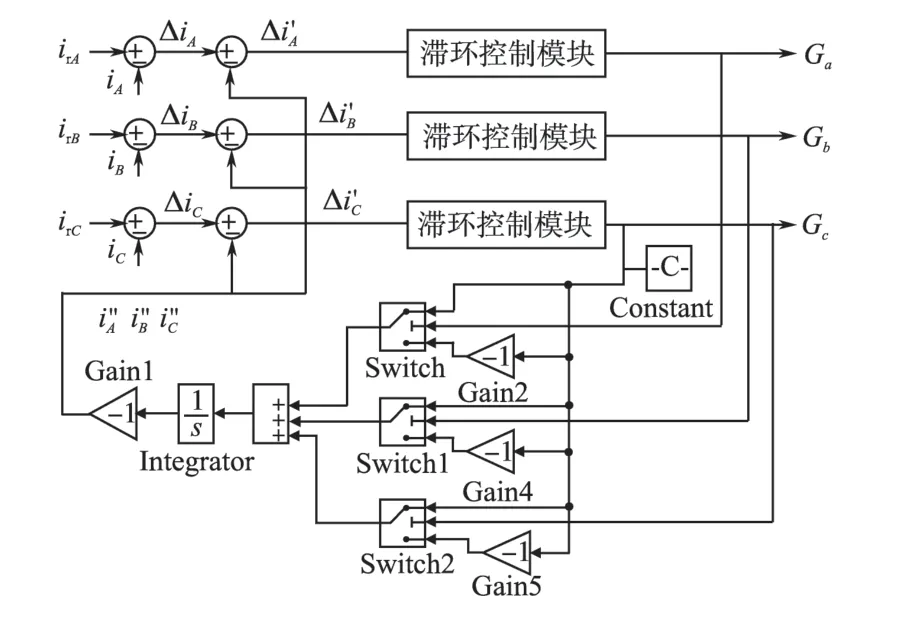
图2 三相3线PWM电流滞环解耦方案Fig.2 3-phase 3-wire PWM current hysteresis decoupling scheme

5.2 整体方案验证

图3 未解耦的仿真结果图Fig.3 Simulated result with no decoupling control

采用图1 所示的主电路，电流参考幅值设为2 A，输出期望幅值也为2 A。图3 为三相3 线仅有电流滞环跟踪（未解耦）的仿真实验结果。图4为加解耦后的仿真实验结果。图4a 为电流跟踪误差分别为ΔiA，ΔiB，ΔiC的波形；图4b为三相输出电流iA，iB，iC的波形；图4c为电路中1号MOS管对应的PWM 触发脉冲；图4d 为的波形。由于篇幅所限，在这里仅列出了一个MOS管的PWM触发脉冲。从仿真结果来看解耦后跟踪误差得到明显改善，而且解耦后能保持开关管频率基本恒定，表明了该解耦方案在电流滞环跟踪控制中的效果良好。

图4 解耦后的仿真效果图Fig.4 Simulated result with the proposed decoupling control

6 结论

电流滞环跟踪是电流控制技术中的重要方法之一。对于三相3 线电流各相存在开关耦合性，在这里采用了叠加方式进行解耦，把电流跟踪误差ΔiA，ΔiB，ΔiC分解为三相交流中性点N与直流中性点N1短接时对应的电流跟踪误差和仅有三相交流中性点N 与直流中性点N1的压差工作时对应的三相电流两部分，解耦方案中采用先得到，再反补偿的方案，间接解除了三相3 线电流各相耦合性。通过Matlab 仿真验证了所提出的三相3 线PWM电流滞环解耦控制的可行性与有效性。

［1］Malesani L，Mattavelli P，Tomasin P.High-performance Hysteresis Modulation Technique for Active Filters［J］.IEEE Trans.on Power Electronics，1997，12（5）：876-884.

［2］Borle L J，Nayar C V. Zero Average Current Error Controlled Power Flow for AC-DC Power Converters［J］. IEEE Transactions on Power Electronics，1995，10（6）：725-732.

［3］刘艳，邵诚.三相电压源型PWM 逆变器相电流重构策略研究［J］.信息与控制，2007，36（4）：506-518.

［4］江明.改进型电流滞环控制变频器［J］.机电工程，1998，1（3）：36-37.

［5］孙玉胜，伍银波，崔光照.单相逆变器三态滞环电流跟踪PWM控制研究［J］.电气应用，2008，27（15）：71-74.

［6］洪峰，单任仲，王慧贞，等.一种变环宽准恒频电流滞环控制方法［J］.电工技术学报，2009，24（1）：115-119.

［7］马立华，陈伯时.电流滞环跟踪控制分析［J］.上海轻工业高等专科学校学报，1997，18（1）：46-52.

［8］Malesani L，Rossetto L，Zuccato A. Digital Adaptive Hysteresis Current Control with Clocked Commutations and Wide Operating range［J］.IEEE Transactions on Industry Applications，1996，32（2）：316-325.

［9］陈增禄，任记达，毛惠丰，等.新型双重△调制电流跟踪控制方法的研究［J］.电网技术，2005，29（12）：62-65.

［10］刘晓博，徐永海，蒋大鹏，等.斜线PWM及其派生电流跟踪方法［J］.中国电机工程学报，2011，31（21）：76-83.

［11］章建峰，陈道炼.三态准PWM 电流滞环控制逆变器分析与实现［J］.电力电子技术，2005，39（2）：33-35.

［12］Bahrani B，Kenzelmann S，Rufer A.Multivariable-PI-based dq Current Control of Voltage Source Converters with Superior Axis Decoupling Capability［J］.IEEE Transactions on Industrial Electronics，2011，58（7）：3016-3026.

［13］陈亚娟.三态滞环控制型逆变器外特性的研究［J］.电力系统及其自动化学报，2003，15（6）：41-44.

［14］崔桂梅，王建良，洪晓英，等.电流跟踪型逆变器中电感值的计算［J］.高电压技术，2003，29（8）：5-6.