基于MTPA的永磁同步电机模型预测转矩控制

王伟光，李伟

（哈尔滨电气动力装备有限公司，黑龙江哈尔滨150040）

永磁同步电机（PMSM）是一种体积小、运行效率高的先进电机，基于PMSM组成的闭环调速系统在高控制精度、快速响应要求的场合得到广泛应用［1-2］。PMSM 作为典型的非线性机电能量转换系统，为了提高调速系统控制性能，矢量控制（vector control，VC）需要进行复杂的解耦控制，其内环控制器由2 个PI 调节器实现转矩和磁链的独立控制，此时系统的控制性能严重依赖PI参数的设定值，同时附加的优化目标很难加入系统控制中［3-4］。模型预测控制［5-6］（MPC）作为非线性控制方法中的典型代表，凭借高动态响应特性、多目标优化能力以及灵活的实现方式，使得其在电力电子与电力传动领域得到了高度重视。

本文以PMSM调速系统为研究对象，提出了一种模型预测控制下的PMSM 最大转矩电流比（MTPA）优化方法，在建立PMSM 调速系统离散预测模型的基础上，重点分析了系统多个优化目标的实现机理，其中包括：开关状态限制、电磁转矩控制、MTPA优化以及最大电流限制，并采用权值法构建了相应的多目标优化函数。样机实验结果表明，所提方法在保留了MPC的高动态响应特性的基础上，有效地实现了PMSM调速系统多个优化目标的综合最优。

1 系统数学模型

图1为PMSM-VSI调速系统结构图，在三相理想对称情况下，建立系统两相旋转dq坐标系下的数学模型如下：

式中：ud，uq为dq 轴定子电压；id，iq为dq 轴定子电流；Rs为定子电阻；Ld，Lq为dq 轴电感；Ψm为永磁体磁链；ωe为电机电角度。

图1 PMSM-VSI调速系统结构图Fig.1 The structure chart of PMSM-VSI speed control system

文献［7］指出，当数字处理系统的控制频率足够高时，可以认为其各变量在一个控制周期内变化率保持不变，根据前向差分原理可将式（1）中的微分项近似为

式中：上标k，k+1表示对应时刻的数字系统采样值。

将式（2）代入式（1）得系统的离散预测模型为

2 优化目标分析

预测控制（MPC）作为非线性控制的典型代表，与传统线性控制相比，其最大的优势为可以有效地实现多个控制目标的同时优化。本文所研究的永磁同步电机MTPA 调速系统的控制目标包括3 部分：开关状态限制、电磁转矩控制及MTPA 优化，其中根据各个控制目标重要程度的不同，同时考虑到算法运算量，下文逐一给出了3个控制目标的优化方法。

2.1 开关状态限制

对于三相全桥逆变系统，每相桥臂可输出0，1 两种开关状态，因此系统可提供23=8 个不同的电压矢量，其中包含6 个非零电压矢量和2 个零电压矢量。然而，考虑到功率开关器件的开关损耗问题，在实际系统的某一控制时刻，并非所有开关状态均可被切换输出，图2 中给出了三相全桥逆变系统开关状态切换图。

图2 三相全桥逆变系统开关状态切换图Fig.2 Switch state diagram of three-phase inverter system

若第k-1周期110 状态被作用于实际逆变系统，则在第k周期时并非所有开关状态均可被施加，系统仅可由110 向010，100，111 新状态跳变，或者维持自身110状态。因此，MPC在每个控制周期优化之前通过查询图2 所示的开关切换表，可以将滚动优化次数由8 次缩减至4 次，一定程度上克服了MPC在线运算量过大的问题。

2.2 电磁转矩控制

电磁转矩控制作为PMSM 调速系统的核心优化目标，为了获得一个高精度、高动态特性的电磁转矩控制效果，构建转矩控制目标函数如下：

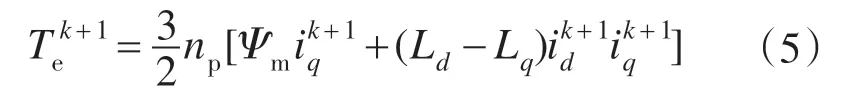
转矩控制目标函数将在系统动态过程中占据主导地位，可以快速地消除转矩跟踪误差。

2.3 MTPA优化

为提高PMSM调速系统的运行效率，实际系统中期望以最小定子电流获得最大的电磁转矩输出，即实现最大电流安培比（MTPA）。为此，一个辅助优化项被加入系统优化中，具体过程见图3。

图3 PMSM空间矢量分析图Fig.3 Space vector analysis diagram of PMSM

如图3 所示为PMSM 在dq 旋转坐标系下的空间矢量分析图，设定子电流矢量idq与q轴呈β角度，此时dq坐标系下的电流分量为

式中：im为定子电流幅值。

将式（6）代入式（5）的转矩方程可得：

假设式（7）电机定子电流幅值im为固定值，可以看出，电机电磁转矩仅与夹角β有关，为了确定式（7）的极值点，以β为变量进行微分运算为

由于id，iq与β满足下述关系

将式（9）代回式（8）即可求得MTPA 情况下的id，iq关系如下：

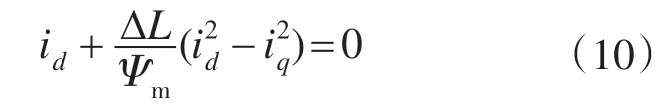
至此构建MTPA目标函数如下：

3 多目标优化

根据前文分析可知，永磁同步电机PMSM调速系统包含多个优化目标，通常采取权值法［8］构建上述目标函数，具体如下：

式中：i为开关状态的对应序号；KTe为电磁转矩控制项目标函数；KMTPA为MTPA优化目标函数。

此外，为了保证功率器件和电机系统的安全，需要对其允许通过的最大电流加以限制，令上述最大电流为Imax。此时可以在式（12）中添加一个安全辅助项如下：

至此，可将式（12）的目标函数优化为

式中：fTe，fMTPA为系统性能指标，直接关系到系统的PMSM 的电磁转矩和定子电流；fsafe为系统安全指标，保证PMSM调速系统的安全性与可靠性。

图4 为控制算法流程框图，以第k 周期为例，系统首先根据第k-1 周期的输出电压矢量Sk-1查询图2 所示的开关状态切换图，即得出第k周期的可行开关状态，随即进入预测控制的在线滚动优化阶段；在结合离散预测模型得到系统各状态未来发展趋势的基础上，结合式（4）、式（11）、式（13）求得系统转矩控制、MTPA 优化以及安全保护优化项的对应值，进而根据式（14）求得开关状态对应目标函数值；经过滚动计算后，最终使系统多个优化目标综合最优的开关状态将会被选出，并将其施加于实际系统中。

图4 控制算法流程图Fig.4 The flow chart of control algorithm

4 实验与分析

为了验证所提永磁同步电机MTPA 预测控制方法的可行性，搭建了1 台三相电压型PMSM调速系统实验样机，其中IGBT 模块采用英飞凌公司的BSM100GB170DLC 模块，数字处理器采用TI 公司TMS320F2812DSP 芯片，控制频率为10 kHz。PMSM 调速系统的主要参数为：额定电压380 V，额定电流38 A，定子电阻0.186 Ω，d 轴电感12 mH，q 轴电感22 mH，转子磁链0.9 Wb，极对数5，直流母线电压600 V。

图5 为控制算法的原理框图，可以看出系统采取PI外环、MPC内环的结构，外环PI控制器根据转速跟踪误差得出转矩给定值Te_ref，内环MPC控制器以图4所示的算法流程图进行多目标在线优化后，得出最优的开关状态Sop并将其作用于实际PMSM调速系统。

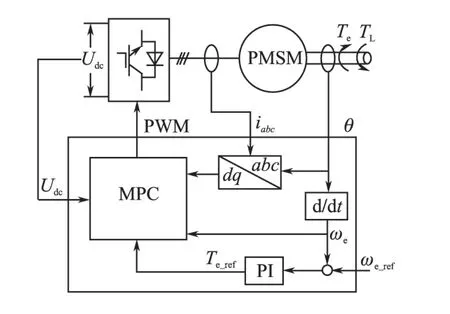
图5 控制算法原理框图Fig.5 The principle block diagram of control algorithm

如图6 所示为PMSM 调速系统总体控制特性，电机被控制为额定转速600 rad/min。在t=0～0.05 s阶段，PMSM由0 rad/min加速至600 rad/min，期间为了获得一个最大的转矩输出，电流幅值im达到最大电流允许幅值，即im=imax=40 A；在t=0.05～0.1 s 阶段，PMSM 进入正向加载阶段，在电机转矩突变瞬间电磁转矩控制项在整个目标函数中占据主导地位，仅需5 ms左右的时间即可完成转矩响应。待PMSM进入稳态后，此时的电磁转矩跟踪误差已经很小，MTPA 优化项占据主导地位，PMSM运行于MTPA优化轨迹上，对应的励磁电流id也被控制为-15 A。在t=0.1～0.2 s 阶段，PMSM逐步进入反向加载阶段，随着负载转矩的变化励磁电流id可以有效地进行自适应调节，整个过程中PMSM始终运行于MTPA最优轨迹上。

图6 PMSM调速系统总体控制特性图Fig.6 Overall control characteristic of PMSM speed control system

如图7所示为PMSM调速系统电流轨迹图，在整个PMSM调速过程中，电机定子电流始终运行于MTPA最优轨迹上，且电机电流矢量也未过多的超出其最大允许电流圆环。此外，PMSM调速系统状态动态切换过程中的电流轨迹极为稀疏，由此可知系统的动态响应过程极为迅速，整个系统更多地处于稳态运行阶段。综上可知，PMSM 调速系统保持着极为优异的稳态、动态性能。

图7 PMSM调速系统电流轨迹图Fig.7 Current path of PMSM speed control system

5 结论

本文在建立PMSM 调速系统离散预测模型的基础上，逐一分析了系统多个优化目标的实现机理，并采用权值法构建了多目标优化函数。样机实验结果表明，该方法可以实现电磁转矩跟踪、MTPA 优化以及最大电流限制等多个优化目标的综合最优，验证了永磁同步电机MTPA预测控制方法的可行性和优越性。

［1］朱伟巨，黄海，张华熊．一种改进的永磁同步电机无传感器滑模控制［J］．电气传动，2013，43（7）：8-11.

［2］朱家厅，王莉娜，薛飞．永磁同步电机的滑模PI模糊逻辑控制［J］．电气传动，2013，43（7）：43-48.

［3］王新，胡路东，徐娟．PMSM矢量控制在高端波轮洗衣机中应用的研究［J］．电气传动，2012，42（12）：10-13.

［4］董苏，赵烨，戴鹏．一种新型IPMSM无位置传感器矢量控制系统研究［J］．电气传动，2013，43（5）：11-15.

［5］曹晓冬，谭国俊，王从刚.一种低开关频率PWM整流器的满意预测控制策略［J］.中国电机工程学报，2013，33（27）：69-77.

［6］Rodriguez J，Pontt J，Cesar A.Predictive Current Control of a Voltage Source Inverter［J］. IEEE Transactions on Industrial Electronics，2007，54（1）：495-503.

［7］Vargas R，Cortes P，Ammann U. Predictive Control of a Three-phase Neutral Point Clamped Inverter［J］.IEEE Transactions on Industrial Electronics，2007，54（5）：2697-2705.

［8］席裕庚，李德伟.模型预测控制——现状与挑战［J］.自动化学报，2012，38（9）：1-15.