逆变器系统预充电控制策略的研究

刘莹，程善美，孙得金

（1.华中科技大学自动化学院，湖北武汉430074；2.武汉征原电气有限公司，湖北武汉430012）

1 引言

逆变器系统结构和控制策略在交流传动系统中的应用已经十分成熟，并在现代工业中具有非常广泛的应用。对于中大功率交流传动逆变器系统，母线电流稳定性要求较高，母线平波电感很大；逆变器工作过程中要求母线电压稳定，直流侧支撑电容较大。电容是一个储能元件，电路闭合瞬间，电容内若没有一定的能量，则电路中电容的充电电流会非常大，会引起过流现象。为了防止电容充电电流过大，系统上电启动时需要采用额外的充电回路对支撑电容充电，达到供电电源电压，此过程称为预充电。目前比较常用的方案是在直流母线上串联一个限流电阻，通过开关器件实现控制。该方案不仅增加系统的体积，而且也增加了系统成本［1-2］。为了进一步简化系统结构和优化预充电过程，本文对三相全桥逆变器系统的预充电控制策略进行了深入研究。

2 交流传动逆变系统结构

图1 给出了常用三相交流传动逆变系统的结构［3-4］。图1 中三相交流传动逆变系统由直流供电电源模块、直流母线平波电感及支撑电容部分、预充电模块、三相电压型逆变器及制动单元和三相交流电机负载等几个部分组成。图1采用的是一种比较常用的预充电结构，由串入直流母线的充电限流电阻和与其并联的开关管构成。启动时，三相全桥开关管全部封锁，逆变器处于待机状态，开关管QCH也封锁。直流母线主接触器闭合后，直流供电电源通过充电电阻RCH对支撑电容C 充电，从而限制支撑电容C 充电电流的大小。支撑电容两端电压上升达到某一阈值，开关管QCH导通，将充电电阻切除，预充电过程结束。在后续的工作中，支撑电容维持逆变器的直流母线电压稳定，逆变器开始工作。

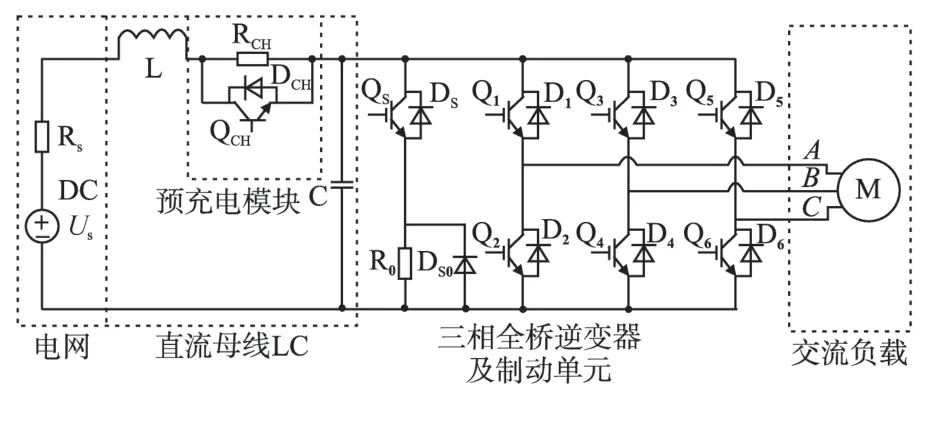
图1 三相全桥逆变系统结构Fig.1 Structure of three-phase full-bridge inverter system

通过制动电阻实现能耗制动是交流变频传动应用中最常见的制动方式［5］。如图1 所示，逆变器系统的制动单元电路由开关管QS和制动电阻R0及其反并联二极管DS0构成。系统制动时，负载电机的能量返回到直流侧，支撑电容电压升高。控制开关管QS，通过电阻R0来消耗回馈的能量，可以抑制电容电压进一步升高，防止器件过压危险并控制电机制动性能。结合制动单元并考虑系统的预充电过程，本文提出一种新的预充电方案，使整个系统结构得以简化。图2 所示给出了简化的系统结构图，去掉了原系统串入直流母线的充电电阻和并联的开关管，由平波电感、支撑电容和制动单元电路构成预充电电路，简称LCR电路。对于制动模块，系统预充电时逆变器处于待机状态，此模块只作为充电电路一部分；电机负载制动时，逆变器处于能耗制动状态，电阻R0作为电机制动负载；系统正常逆变工作时，制动电路的开关管QS断开，电阻开路。预充电和制动工作在各自的工作状态，且各状态之间相互独立，没有影响。

图2 简化三相全桥逆变系统结构图Fig.2 Simplified structure of three-phase full-bridge inverter system

3 LCR结构模型

对于系统LCR预充电模块，直流供电电源采用直流恒压源US和串联等效内阻Rs表示，输出为电容充电电压。控制开关管QS和电阻R0使电容充电过程中电容电压和电感电流瞬时值在允许的范围之内，且充电时间较短。图3 给出了开关管QS开通和关断时的等效电路。设QS开关状态为Si(i=0’1)：S0表示开关断开状态，电阻开路；S1表示开关闭合状态，电阻与电容并联。

图3 QS断开与闭合时等效电路Fig.3 Equivalent circuits of QS in off and on states

当LCR 回路处于S0状态时，电感电流iL0对输入电压Us及电容电压UC0对输入电压Us的传递函数如下：

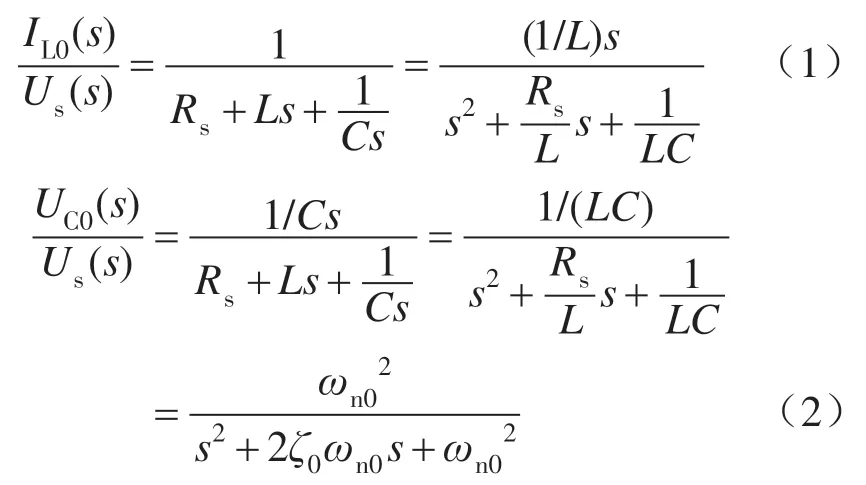
电压传递函数为典型2阶环节，其中ζ0，ωn0分别为系统阻尼系数和谐振频率。电流传递函数的特征函数与电压的相同。

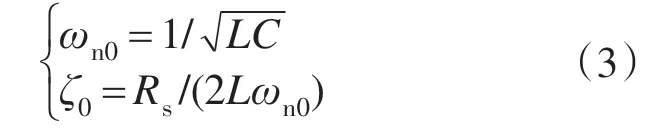
同理，当回路处于S1状态时，电感电流iL1对输入电压Us及电容电压UC1对输入电压Us的传递函数如下：

电压传递函数为比例系数k与典型2 阶环节乘积，其中ζ1，ωn1分别为系统阻尼系数和谐振频率。电流传递函数的特征函数与电压的相同。

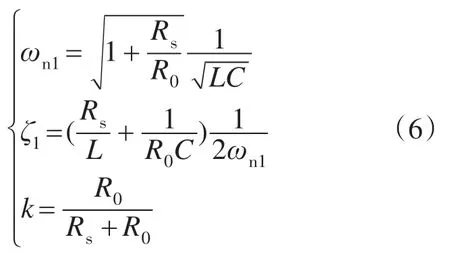
式（6）中比列系数k可以用来衡量直流供电电源内阻的相对大小，k越接近1，内阻相对越小。系统上电启动时，直流母线上的接触器在t0时刻闭合瞬间，直流供电电源电压突加到预充电回路上。系统输入可以用阶跃信号来表示，其时域和S域表达式如下：

若保持S0状态，电路稳定后，电感电流及电容两端电压值为

同样的，若保持S1状态，电路稳定后，电感电流及电容两端电压值为

由式（8）可知，充电结束，逆变器启动前处于待机状态，系统稳定在S0状态。直流母线支撑电容电压达到供电电源电压，直流侧电流为0。电容电压传递函数为典型2 阶环节，则系统的阻尼系数和谐振频率直接决定系统阶跃响应的动态性能。系统阻尼系数越小，电压超调越大。S0状态下系统阻尼系数如式（3）所示，由于直流供电电源等效内阻较小，则ζ0很小，系统电压、电流的超调量很大。若不施加控制，电容会过充电，电压可上升到接近直流供电电源电压的2倍。然后电感电流反向，电容对直流供电电源放电产生LC 谐振，对直流侧器件及直流供电电源造成危害。对比式（3）、式（6），阻尼系数ζ1＞ζ0，S1状态下电压、电流的超调较小。为了抑制预充电时电压、电流的冲击，系统动态过程应控制在S1状态。另外，由式（9）结果可知，稳态电压小于供电电源电压，考虑到充电过程中电容电压峰值不超过直流供电电源电压，阻尼系数选取范围可以适当增大。

4 电路参数对LCR回路影响

预充电方案的实现目标是系统选取的电感、电容、电阻参数使得充电过程中电容电压和电感电流在器件所允许范围之内。电压传递函数如式（2）、式（5）所示，为典型2 阶系统，动态特性可以用阻尼系数和谐振频率描述。如式（1）、式（4）所示，电流传递函数比电压模型多一个零点，相位超前电压，阶跃响应的特性比较复杂。由电流传递函数可知，充电时电感电流与电感值呈反相关性，电容越大，系统零点距虚轴越近，电流峰值越大。

系统参数有直流供电电源内阻Rs、制动电阻R0、平波电感L和支撑电容C等4个参数。等效内阻和制动电阻分别由直流供电电源和负载电机的制动要求决定，电阻值确定后，则只有LC组合参数对系统产生影响。图4 给出了S1状态时，在输入电压DC 600 V 情况下动态过程中电感电流峰值和电容电压峰值在不同的LC 参数下的曲线。直流供电电源内阻Rs=0.4 Ω，制动电阻R0=1.7 Ω 保持不变。电感参数变化范围为[0.5 mH’4 mH] ，电容参数变化范围为[500 μF’4 000 μF]，对电感以等间距取离散点得到不同电容下电压、电流的最大值绘制曲线。电路参数选取时，可以作为参照。

图4 不同LC参数时瞬时电流、电压峰值曲线Fig.4 Instantaneous peak current and peak voltage curves for different LC parameters

对于图4b电压峰值曲线，如式（9）所示，动态电压相对于稳态值有一定的超调，但其最大值都不超过输入电压DC 600 V。电压峰值必须低于电容耐压值，而电容的耐压值一般要大于输入直流电源的最大值，因此，动态电压峰值对LC参数要求不是很高。由图4a电流峰值曲线可知，预充电动态过程中平波电感上电流峰值的大小随电感值增大而减小，随电容值增大而增大。电感参数取1 mH 时，电容取500 μF 对应的电流最大值为400 A，电容增大到1 000 μF 时，电流值达到500 A左右。由于逆变器对母线电压稳定性的要求较高，支撑电容取值较大，设计电感时需增大其承受电流峰值。

5 预充电控制方案

预充电过程分为4 个阶段：1）LCR 回路先处于S0状态，电容电压低，系统阻尼小，充电速度快；2）电容电压上升到某一阈值，开关QS闭合处于S1状态，系统阻尼变大。电压、电流响应的动态过程控制在此状态，超调较小；3）控制开关QS工作在PWM方式下，电容电压、电流缓慢变化。电压上升趋近直流供电电源电压而电流减小趋近于零；4）开关QS断开，电容两端电压达到直流电源电压值，电感电流为零，充电结束。可以使用2个电压传感器分别检测电感之前的直流供电电源电压Us(t)和电容两端电压UC(t)进行控制，检测到Us(t)由零上升到某一阈值时表示充电开始。由于系统参数固定，变化不大，可以通过计算充电时间，得到控制开关管动作的时刻。后一种方法相对于检测电压来说，控制实现较简单，能够排除检测中的干扰因素，比较可靠。

充电的第3）阶段，采用PWM 脉冲控制IGBT 开关管QS，开关频率fs=2 kHz ，周期Ts=0.5 ms。设某一段时间内占空比为D，电容电压在某一稳定的平均值上下波动。由于电感值较大，开关切换过程电感电流IL保持恒定不变。图5 给出了一个PWM 脉冲周期内电容电压波形。S0状态，电感电流全部流入电容，对电容充电。电容电压上升增量为ΔUC+，达到UCH；S1状态，电容与电阻并联，此时电容两端电压高于电压Uavg，电容通过电阻放电。放电过程中电容电流由电容正端流向电阻回到电容负端，电容电压下降ΔUC-到UCL。

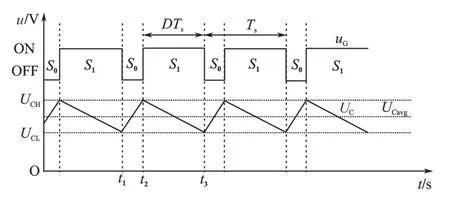
图5 一个PWM脉冲周期内电容电压波形Fig.5 Voltage of the Capacitor in one PWM period

图5中，(t1’t2]时间段，电感电流为IL恒定，电容电压增量ΔUC+如下：

(t2’t3]时间段，电感电流仍为IL恒定，电压采用线性近似，可得到放电时电容电压减小量ΔUC-。系统稳定后，电容充电和放电时的电压增量相等，即：

电容电压减小量ΔUC-如下：

式中：Uavg为平均电压

由式（10）、式（11）和式（12）可得：

当占空比D=1系统稳定时，则电压、电流满足式（9）的条件，即系统处于S1状态且电路稳定，式（9）稳态电压即为式（13）中的平均电压。当R0远大于Rs时，由稳态电压、电流关系可得：

由式（14）得到结论如下：PWM脉冲控制下，电感电流与占空比D成正比关系，比例系数与供电电源电压和制动电阻有关为一常数，与其他参数无关。通过控制PWM脉冲占空比实现对平波电感电流的控制。

图6 给出了PWM 控制下占空比D分别采用线性衰减和指数衰减两种控制方式时电容电压和电感电流的仿真波形。由线性衰减和指数衰减两种控制方法对比，前者控制算法计算简洁，实现比较方便；后者电感电流衰减速度更快，控制效果较优。二者所对应的占空比D表达式如下：

图6 两种占空比控制方式下充电电压和电流波形图Fig.6 Voltage and current during charging process for two control strategies

6 预充电实验

根据图2的结构，搭建120 kW三相全桥逆变器系统，直流供电电源输入DC 600 V直流电压，对预充电方案进行测试。直流供电电源内阻Rs=0.4 Ω，制动电阻R0=1.7 Ω。试验时平波电感L取3.1 mH，支撑电容C取2 490 μF。参照图4曲线可知，对应的电压、电流峰值理论值为580 V和470 A左右。

实验中，600 V 左右直流供电电源通过手动开关直接加到直流母线两端，预充电过程开始。开关管QS断开，电容快速充电，预充电处于第1）阶段。检测电容两端电压瞬时值，当电压由0 上升到400 V时开关管QS闭合，进入下一阶段。第2）阶段QS闭合持续时间20 ms，电压、电流上升速度减小，电流达到动态过程的最大值，波动幅值逐渐减小。充电第3）阶段占空比采用线性衰减曲线。在100 ms 时间内，占空比由1 减小到0。随着占空比的减小，电容电压上升到直流供电电源电压，电流减小趋近于零。最后QS闭合，电容电压稳定在电源电压，预充电过程结束。

图7 给出了预充电实验电压电流波形，其中图7a 为支撑电容电压UC波形和制动电阻R0上电压UR波形；图7b为电容电压UC波形、控制开关管QS的PWM脉冲UG波形和平波电感上的电流iL波形。示波器中测得充电第2）阶段电压最大值为559.4 V，没有超过直流供电电源电压；测量的电流最大值约为407 A。电压、电流的实验值与图6所示的仿真结果非常接近。由于实际的电压跳变比理论的DC 600 V 要小，电压、电流峰值测量值稍小于理论值。电感电流超过额定电流时间很短，对系统影响不大。充电结束电容两端电压稳定在直流供电电源电压，电感电流为零。

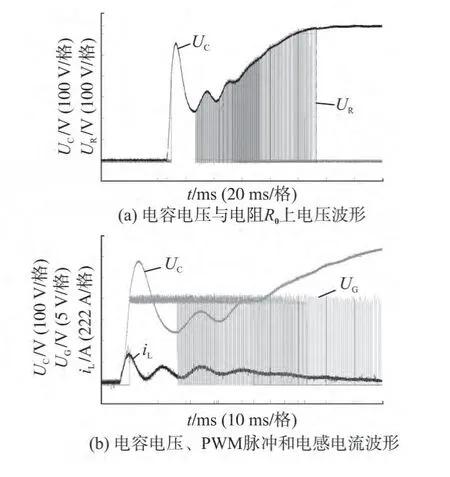
图7 预充电实验电压电流波形Fig.7 Experiment current and voltage for pre-charging process

7 结论

本文结合逆变器能耗制动单元提出一种简化的三相逆变器系统结构和新的LCR 预充电电路，并提出了基于PWM 控制的预充电控制方案。逆变器预充电过程中的电压、电流在允许的范围之内，系统其他功能不受影响，实验结果证明了新的LCR 预充电结构和控制方案可行性。新方案下的三相逆变器系统结构更加简洁，器件利用效率更高，适用于中大功率的交流传动。

［1］王彬，裴冰，马连凤.大功率牵引变流器用预充电电阻的仿真计算分析［J］.铁道技术监督，2010，38（6）：40-43.

［2］王彦红，靳宝会.变频器预充电电路的改进设计［J］.煤矿机电，2012（6）：108-110.

［3］Ned Mohan，Tore M Undeland，William P Robbins. Power Electronics：Converter，Applications，and Design［M］. John Wiley&Sons，Inc.，2003.

［4］王兆安，黄俊.电力电子技术［M］.北京：机械工业出版社，2000.

［5］王世平，梁金成，黄志国，等.电机实验电源制动单元工程化计算及应用［J］.电气传动，2012，42（12）：73-76.