永磁同步电机新型矢量控制

陈俊硕， 刘景林， 张 颖

(西北工业大学 自动化学院，陕西 西安 710072)

现代交流伺服系统中，永磁同步电机(PMSM)由于具有体积小、重量轻、结构简单、维护方便、运行可靠且具备高效率、高功率密度等优点[1-2]，在航空航天领域以及工业自动化、机器人等场所得到了广泛应用．常规的基于比例积分控制(PI)的矢量控制方案依然能满足一定范围内的控制要求，但其依赖于系统的准确模型，极易受到外来的扰动以及电机内部参数变化的影响，系统的鲁棒性不够理想[3-4]．

近年来预测控制理论中一些新型的模型预测控制(Model Predictive Control，MPC)方法被相继提出，该模型可以有效地解决类似永磁同步电机这样多变量、强耦合、非线性、变参数的复杂系统控制难题，如H∞鲁棒模型预测控制、约束线性模型预测控制及非线性模型预测控制(Nonlinear Model Predictive Control， NMPC)等[5-7]．美国NASA Glenn研究中心从控制角度讨论了智能发动机的发展，介绍了有关非线性模型预测控制的应用．该方法通过预测优化手段准确控制目标，在有扰动或模型失配的情况下具有良好的鲁棒性．但是，非线性模型预测控制基本都以单步长泰勒级数法为基础，求解泰勒级数也就是求解多次微积分过程，计算非常复杂．因此，现有的非线性模型预测控制大部分只能用于较慢的过程控制．随着计算方法和电力电子技术的快速发展，近些年非线性模型预测控制也被尝试应用于各类快动态系统中．

由于在实际利用非线性最小二乘法实时求解预测控制的应用中，计算效率对于控制方案可行性至关重要，为此，笔者提出了基于预测控制的新型矢量控制方案，针对非线性模型预测控制求解泰勒级数复杂问题，引入简单有效的计算泰勒级数的自动微分方法[8]，提高了预测控制算法的效率，降低了对模型的依赖性，并设计了一个永磁同步电机调速系统新型矢量控制器．实验结果表明，该控制方案满足了动态较快的电动机实时性要求，具有一定的抗干扰能力．

1 基于自动微分的非线性模型预测控制基本原理

首先以常见的一阶非线性系统为例，对基于自动微分的非线性模型预测控制基本原理进行说明，即

(1)

其中，u(t)∈R，是控制输入；y(t) ∈Rm，是系统输出；h为步长．若令z=f(x)，则其为一个连续微分方程，f:Rn→Rm．假设输入u(υ)=u[0]+u[1]υ+ …+u[r]υr，r≤d(d为泰勒展开次数)，其中所有的输入系数u[k]，k=1，2，…，r为已知，令矢量v= [u[0]T，u[1]T， …，u[r]T]T， 利用自动微分方法，x(υ)和y(υ)的泰勒级数可以由x[0]和v通过链式法则得到[8]，其结果如下:

(2)

其中，z[k]为z对时间t的d次泰勒展开系数被系数向量x[k]惟一确定．

用自动微分法对z[k]求偏微分，定义如下:

(3)

其中，A[k]∈Rn×n，k=0，1，…，d， 为泰勒级数的雅克比路径，其定义为

(4)

由式(4)可得，f′(x(t))可以表示为

f′(x(t))=A[0]+A[1]t+…+A[d]td+ξ(td+1) ．

(5)

对于类似式(1)中的微分方程x=f(x(t))，由于展开系数x[k+1]=z[k]/(k+1)，令x[0]=x(0)，则在t时刻的任意阶泰勒级数都可递推获得．从式(4)可得，x[k]对于x[0]和v的灵敏度为

(6)

其中，矩阵B[0]=[I|0]．

针对在非线性模型预测控制中求解泰勒级数的不便，引入自动微分方法使泰勒级数计算变为简单的数值运算．把求解雅克比矩阵转化为求解泰勒极数的灵敏度，得出其对于初始量x[0]的灵敏度矩阵，进一步简化了非线性模型预测控制中的计算量，使其能满足动态较快的永磁同步电机矢量控制要求．

2 永磁同步电机数学模型

2.1 永磁同步电机基本矢量控制数学模型

基于表面式永磁同步电机，假设磁路不饱和，在空间磁场呈正弦分布，不计磁滞和涡流损耗影响的条件下，采用id=0 的永磁同步电机矢量控制[9]，转矩大小只与定子电流的幅值成正比，实现了永磁同步电机解耦控制．此时，永磁同步电机的d-q轴数学模型为

(7)

其中，ud和uq分别为d和q轴的电压；id和iq分别为d和q轴的电流；Ld和Lq分别为d轴和q轴的电感；R为定子电阻；J为转动惯量；Te为电磁转矩；TL为负载转矩；np为极对数；ω为转子机械角速度；B为粘滞摩擦系数；φ为永磁体与定子交链的磁链．

2.2 永磁同步电机新型矢量控制数学模型

对永磁同步电机基本模型进行基于自动微分的泰勒展开[10]，对式(7)中的id、iq和ω在t时刻针对于t0时刻d次泰勒展开，其中展开系数id[0]、iq[0]和ω[0]由t0时刻初始值确定，即

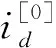
(8)

假设控制量、负载转矩在t0到t时刻不变，当展开次数k=1时，泰勒系数id[1]、iq[1]和ω[1]可由式(7)得到，即

(9)

当展开次数k>1时，由式(7)得

(10)

由链式法则及自动微分算法进行迭代，可以得到阶数k>1时的泰勒系数，即

(11)

式(8)、(9)和(11)构成了一个完整的永磁同步电机的泰勒系数计算方案．令tf=tn+1和ti+1=ti+h，i=0，1，…，n，在初始值id[0]、iq[0]和ω[0]已知时，在ti时刻永磁同步电机的id、iq和ω的数值大小可用它们在t时刻针对于t0时刻d次泰勒展开式递推获得，最后得到在tf时刻的计数值．

3 灵敏度计算

在实际利用非线性最小二次方实时求解预测控制的应用中，计算效率是控制方案能否可行的重要条件．实验结果表明，在非线性控制中，超过90%的计算量都消耗在微分计算中[11]．因此，为了加快永磁同步电机新型矢量控制的计算速度，根据式(7)推导出了一个适合永磁同步电机的基于自动微分的泰勒级数灵敏度的计算方法．

根据永磁同步电机新型矢量控制的数学模型，由式(2)中的x和v可定义永磁同步电机控制系统的状态向量s= [id，iq，ω]，控制量u= [ud，uq]．可定义式(7)的灵敏度矩阵为

(12)

由上述灵敏度矩阵，通过式(6)的灵敏度推导，定义永磁同步电机泰勒级数展开式t+h时刻对t时刻的灵敏度，即

(13)

对于文中的控制器，滚动优化模块是为了在电流、转速等限制约束范围内，最优地实现电机转速恒定．该问题可表示为

(14)

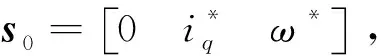
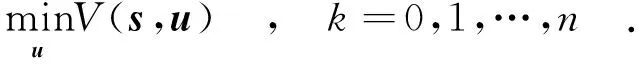
(15)

上述目标函数可以转换为求控制量u对E的雅克比矩阵J，使得V为最小．根据求解非线性方程组的全局收敛的Levenberg-Marquardt算法，结合雅克比矩阵J和性能矢量E，在输入约束的条件下，得到优化控制序列U= [uT(t0)，uT(t1)，…，uT(tn)]T，可通过下式递推更新:

Uk+1=Uk-(JTJ+λI)-1JTE,

(16)

其中，λ是性能控制参数，使得性能指标每一步都收敛．计算得到的控制量U*中只有第1个控制量uT(t0)应用到下一个采样周期中，完成当前控制；重复上述步骤，进行下一步的控制．

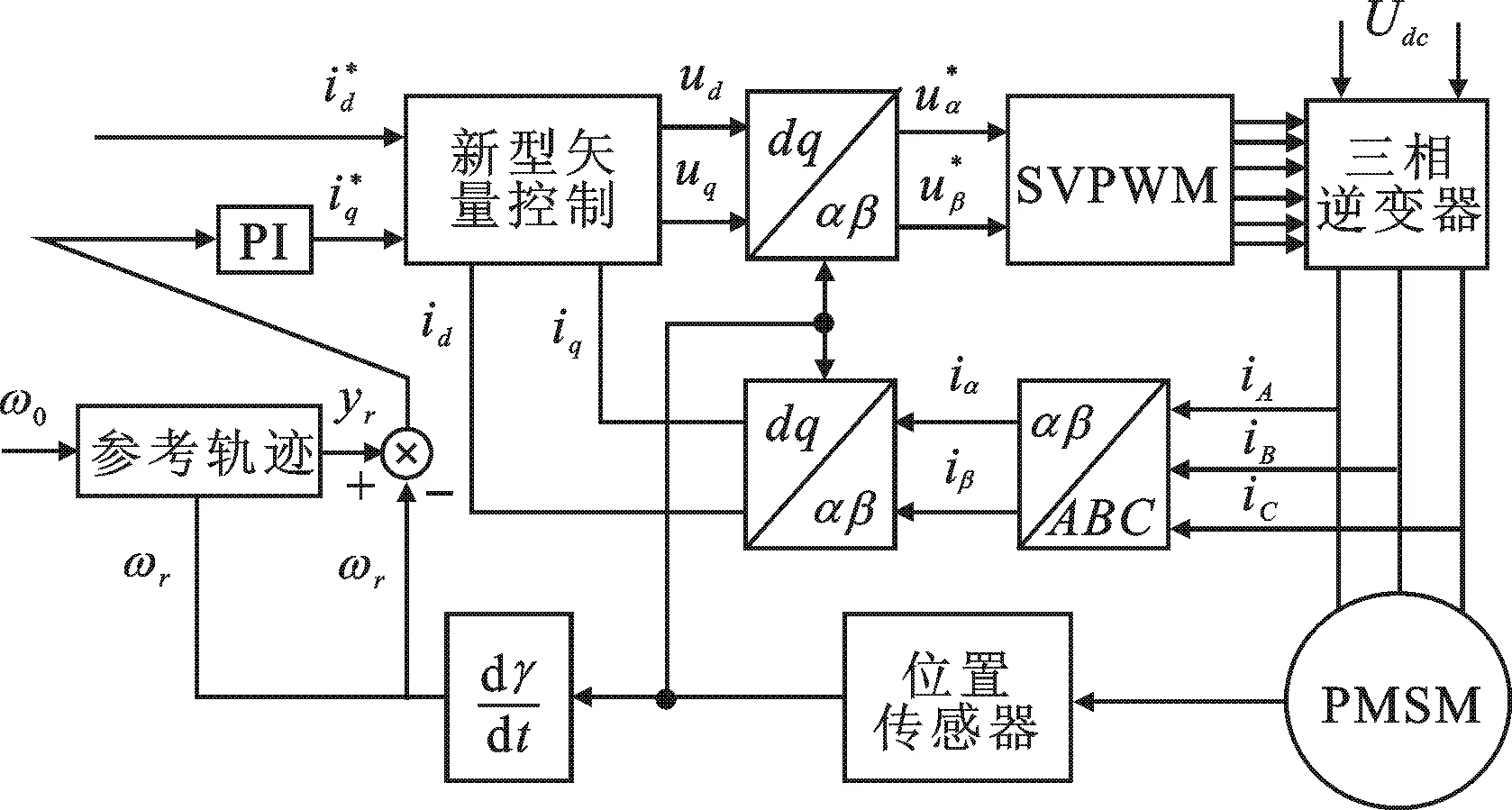
图1 永磁同步电机系统非线性模型预测控制框图

4 新型矢量控制

结合文中所提的控制方法，新型矢量控制系统框图如图1所示．

ω*(t+1)=αωr(t)+(1-α)ω0，α=exp(-T/τ) ,

(17)

其中，ω*(t+1)为t+1时刻转速期望输出，ωr为t时刻的系统实际输出，ω0为期望系统稳定输出，τ为参考轨迹的时间常数．

图2 dSPACE实时仿真系统的硬件框图

5 实验验证

基于上述设计 ， 在德斯拜思(dSPACE)实时仿真系统中进行了实验验证．设定系统仿真算法为固定步长Fixed-step，Euler算法，基本步长为 0.000 1．永磁同步电机的dSPACE半实物仿真系统如图2所示．为了保护dSPACE系统的接口安全，由DS1005板卡各模块发出的信号经过隔离电路后最终加到驱动功率主电路上．系统控制需要的电流、电压、转速等物理信号都需要通过隔离电路传回dSPACE的各组件模块中，完成系统的闭环回路．实验所用永磁同步电机参数为：极对数np=4，交直轴电感Lq=Ld= 0.009 2 H，定子电阻R=3.3 Ω，转子永磁体磁链φ=0.18 Wb，转动惯量J=0.005 kg·m2．

系统采样时间为0.1 ms，参考轨迹中τ=13，状态增益矩阵Q= [1/Ld，1/Lq，1/J]，控制增益矩阵R= [1，0.1]，兼顾系统允许误差为10-9，选用相对较小又能快速稳定的泰勒展开次数d=3．系统初始速度为0，在 2 s 时加入 600 r/m 的期望转速，同时加入 12 N·m 的负载转矩．图3为采集的电机转速从0到 600 r/m 的启动过程中参考转速n*、转速n和相电流I的波形．由于实验中电源电压不能加的太快，实际转速比参考转速上升的稍慢，但从中可以看到，在新型矢量控制下电机启动转速波动小，稳态性能好．

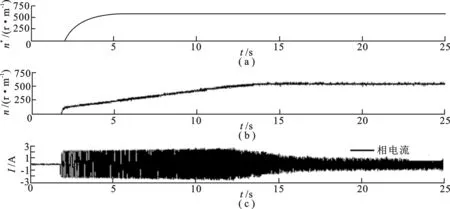
图3 启动过程转速和相电流的波形

图4是在10 s时，增加2 N·m负载转矩，新型矢量控制系统的转速和相电流的波形．可以看出，基于新型矢量控制系统对于转矩的突变有更强的适应性，转速基本不发生变化；从相电流波形可以看到，在突变过程新型矢量控制系统中电流较传统矢量控制变化较小．由于在反馈校正环节中加入转速偏差可以有效地消除静差，保证系统具有较好的抗干扰效果．

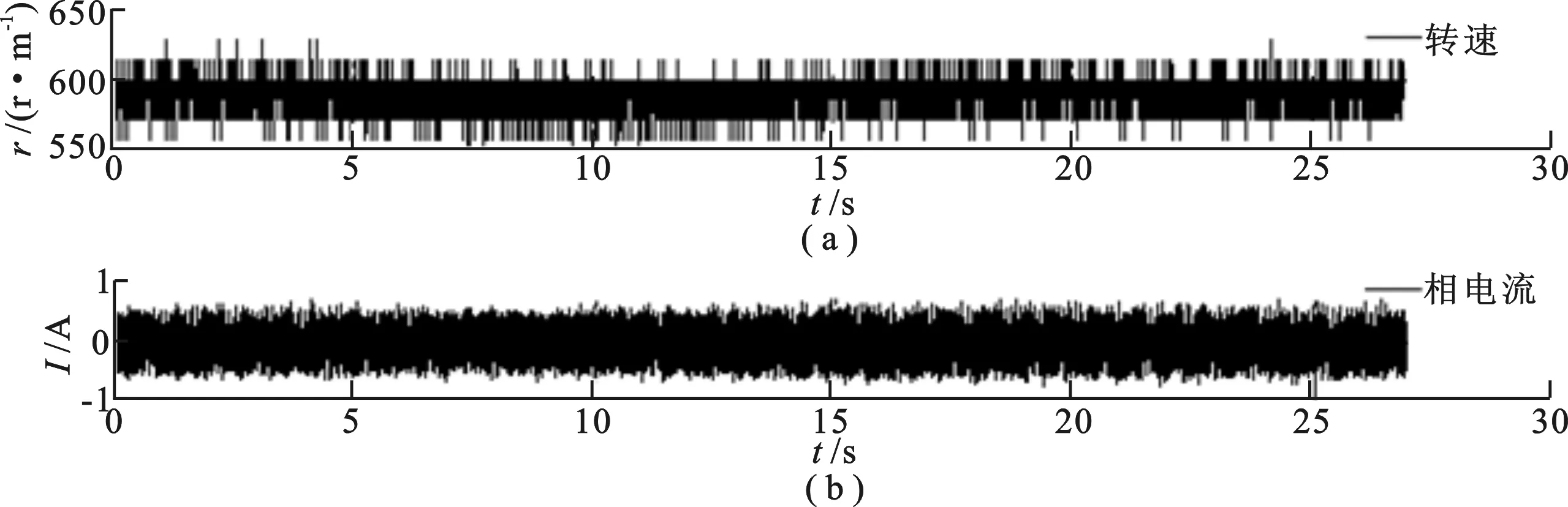
图4 负载转矩变化时转速和相电流的波形(新型矢量控制)

图5为采用传统矢量控制，当转矩发生同样的变化时，却导致转速有10%的下降，经过 10 s 才能恢复到 600 r/m．同时从相电流波形可以看到，在突变过程中传统矢量控制系统中相电流明显增大．

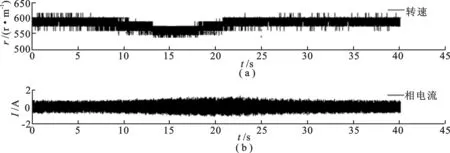
图5 负载转矩变化时转速和相电流的波形(传统矢量控制)

6 结 束 语

设计了永磁同步电机基于预测控制的新型矢量控制器，针对在预测控制中求解泰勒级数的不便，引入自动微分方法使泰勒级数计算变成简单的数值运算．实验结果表明，文中设计的新型矢量控制器应用于永磁同步电机调速系统中是有效可行的；与常规矢量控制相比，不仅能够较好地保证调速系统的动态性能，而且可以有效地改善系统的鲁棒性，使系统具有更好的抗干扰能力．

[1] Zhang Xiaoguang, Sun Lizhi, Zhao Ke, et al. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques[J]. IEEE Transactions on Power Electronics, 2013, 28(3): 1358-1365.

[2] 张细政, 王耀南, 杨民生. 永磁同步电机无位置传感器双滑模鲁棒控制[J]. 电机与控制学报, 2008, 12(6): 696-700.

Zhang Xizheng, Wang Yaonan, Yang Minsheng. Double-sliding-mode Based Sensorless Robust Control of PMSM[J]. Electric Machines and Control, 2008, 12(6): 696-700.

[3] 孙强, 程明, 周鹗, 等. 新型双凸极永磁同步电机调速系统的变参数PI控制[J]. 中国电机工程学报, 2003, 23(6): 117-123.

Sun Qiang, Cheng Ming, Zhou E, et al. Variable PI Control of a Novel Doubly Salient Permanent Magnet Motor Drive[J]. Proceedings of the CSEE, 2003, 23(6): 117-123.

[4] Lai C K, Shyu K K. A Novel Motor Drive Design for Incremental Motion System via Sliding-mode Control Method[J]. IEEE Transactions on Industrial Electronics, 2005, 52(2): 499-507.

[5] 于水情, 李俊民. 变采样周期网络控制系统的模态依赖的H∞预测控制[J]. 西安电子科技大学学报, 2012, 39(5): 147-155.

Yu Shuiqing, Li Junmin. Mode DependentH∞Predictive Control of Networked Control Systems under Variable-period Sampling[J]. Journal of Xidian University, 2012, 39(5): 147-155.

[6] 黄进, 董正良. 一类柔性悬索结构的自适应滑模控制[J]. 西安电子科技大学学报, 2007, 34(1): 11-15.

Huang Jin, Dong Zhengliang. Adaptive Sliding Mode Control of a Flexible Cable Structure[J]. Journal of Xidian University, 2007, 34(1): 11-15.

[7] Preindl M, Bolognani S. Model Predictive Direct Speed Control with Finite Control Set of PMSM Drive Systems[J]. IEEE Transactions on Power Electronics, 2013, 28(2): 1007-1015.

[8] Cao, Y. A Formulation of Nonlinear Model Predictive Control Using Automatic Differentiation[J]. Journal of Process Control, 2005, 15(8): 851-858.

[9] Mishra A, Makwana J A, Agarwal P, et al. Modeling and Implementation of Vector Control for PM Synchronous Motor Drive[C]//Proceedings of International Conference on Advances in Engineering, Science and Management. Piscataway: IEEE, 2012: 582-585.

[10] Liu Jinglin, Chen Junshuo. Predictive Control for Permanent Magnet Synchronous Machine Based on Automatic Differentiation Method[C]//Proceedings of International Conference on Electrical Machines and Systems. Piscataway: IEEE, 2011: 1-4.

[11] 裘君, 赵光宙, 齐东莲. PMSM的哈密顿反馈耗散增益调度控制[J]. 控制工程, 2010, 17(2): 149-153.

Qiu Jun, Zhao Guangzhou, Qi Donglian. PMSM Gain Scheduling Control Based on Hamiltonian Feedback Dissipation[J]. Control Engineering of China, 2010, 17(2): 149-153.