用于多源信息中制导的MM-LS时间配准算法

雍霄驹， 方洋旺， 高 翔， 张 磊， 封普文

(空军工程大学 航空航天工程学院，陕西 西安 710038)

在导弹的中制导过程中，探测传感器经常受到自身限制和敌方干扰，无法提供对目标的精确观测信息．若能同时使用多个传感器对目标进行探测，并由信息融合算法得到对目标状态的估计信息，可显著提高目标状态估计的精度[1]．但各传感器之间起始采样时间、采样频率不同，数据链传输数据的时延也不同，若直接使用各传感器数据，往往得到比非信息融合更差的估计结果[2]．因此，在信息融合处理前，对各传感器的探测数据进行时间配准处理的效果是关系到信息融合最终效果的关键问题．

目前常用的时间配准算法主要包括内插外推法[3]、滤波方法[4]、曲线拟合法[5-6]、最小二乘法[7]等，各算法都有其优缺点．内插外推法是一种较常用的方法，采用三点插值法或拉格朗日插值法，将配准时刻定为插值点，从而得到配准时刻的数据，实现时间配准．根据插值法的算法原理，插值数据应处在插值区间中部，才能保证较高的精度[8]，因此用于事后处理效果较好，但无法满足导弹飞行中制导的实时性要求．文献[4]采用UKF算法同时对时间和空间进行配准，不失为一次较好的尝试，但其推导过程基于目标匀速运动的假设，若模型失配，则误差较大．曲线拟合算法根据一段区间内的采样数据，由最小二乘准则拟合出一条以时间为变量的多项式曲线，从而得到配准时刻的数据，实现时间配准．但是，配准时刻在端点处时存在发散现象[9]，因此同样存在实时性问题，同时，曲线拟合算法还需解决拟合阶次与窗口长度选择的问题[10]．Blair等[11]提出的最小二乘时间配准算法在目标匀速直线运动及传感器采样频率与配准频率之比为整数两个前提条件下，利用最小二乘算法得到配准时刻的虚拟采样值，从而实现时间配准．但是这两个假设极大地限制了最小二乘时间配准算法的应用．针对此问题，笔者采用多模型的思想，将假设目标匀速直线运动改为假设目标分别为匀速直线运动、匀加速直线运动和加加速直线运动，并分别推导其所对应的最小二乘时间配准结果，将结果扩展到速度、加速度、加加速度等状态的求解;随后利用模型求解过程中得到的速度、加速度、加加速度进行外推，得到配准周期与采样周期不成比例时的配准结果．

1 多模型最小二乘时间配准算法

1.1 单模型最小二乘时间配准算法

基于单模型的最小二乘时间配准算法有两个基本假设[2]:

(1) 传感器S的采样周期为τ，配准周期为T，则配准周期与传感器采样周期之比为整数，即T=nτ;

(2) 目标在时间配准的时间段内一直保持匀速直线运动状态．

最小二乘时间配准算法就是将配准周期T的时间范围内的n个S的采样数据进行拟合，得到一个虚拟的采样值，从而实现时间配准．

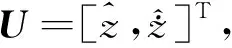
(1)

其中，vi是量测噪声．将上式改写为向量形式:

Zn=WnU+Vn,

(2)

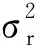
(3)

1.2 多模型最小二乘时间配准算法

根据单模型的最小二乘时间配准算法的原理可以看出，其两个基本假设极大地限制了实际应用．在实际的时间配准问题中，配准频率与传感器的采样频率很难成整数倍关系，且在时间配准过程中，目标几乎不可能一直保持匀速直线运动．因此，笔者给出了非整数周期比条件下的多模型的时间配准算法．

当采用匀加速直线运动模型时，

当采用加加速直线运动模型时，

1.3 模型求解

根据最小二乘准则，有目标函数

(4)

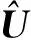
(5)

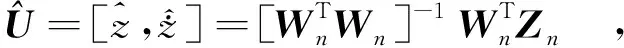
(6)

(7)

由此，可以得到3种模型下的最小二乘时间配准的位置以及各模型所对应的位置的一阶、二阶、三阶导数．

根据最小均方误差准则，得配准值为

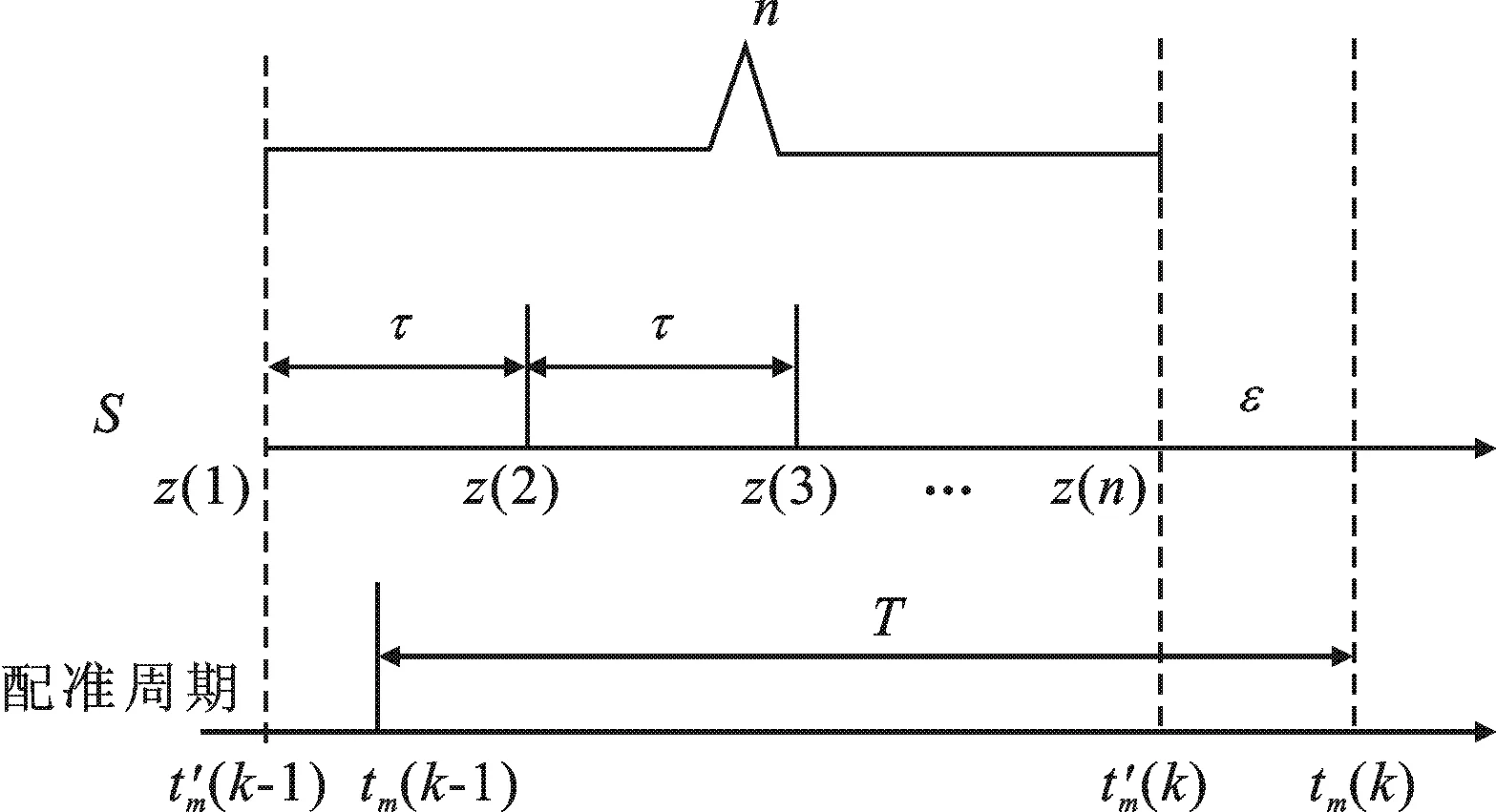
图1 非整数周期比条件下的最小二乘时间配准

通过后端的滤波算法进行目标运动模型的辨识来获得量测噪声方差[σ(1)]2、[σ(2)]2和[σ(3)]2，反馈给时间配准算法，采用式(9)进行计算，减少以往时间配准过程中对于目标匀速运动假设与实际运动不符所带来的误差，提高了时间配准算法的精度和适应性．

1.4 非整数周期比条件下的多模型算法

若配准周期与传感器的采样周期之比为非整数倍，其情形如图1所示．

(1) 匀速直线运动模型

(10)

(2) 匀加速直线运动模型

(11)

(3) 加加速直线运动模型

(12)

根据式(8)和式(9)，可以得到周期之比为非整数倍情况下的多模型最小二乘时间配准的结果．

2 仿真分析

2.1 目标为弱机动状态

假定目标在0～60 s内匀速直线运动；在60～200 s内匀加速直线运动，加速度为 6g．目标的初始位置为(100，3 000)，初始速度为 420 m/s，初始速度倾角为 π/4．在 10～ 180 s 内进行时间配准．

仿真1 雷达传感器的采样周期为0.15 s，配准周期为1 s，雷达的测距误差为 10 m，则多模型最小二乘时间配准算法的均方根误差(RMSE)如图2所示．

由图2可以看出，当目标为弱机动状态时，从时间配准效果上看，匀速模型优于多模型并优于常加速模型且优于加加速模型．匀速模型的X方向与Y方向的均方根误差在8上下震荡，而常加速模型与加加速模型的X方向与Y方向的均方根误差在11和15上下震荡．多模型最小二乘时间配准算法的均方根误差与雷达探测精度相当，在10上下震荡．总体来说，在此情形下，4种算法的时间配准误差相差不大．

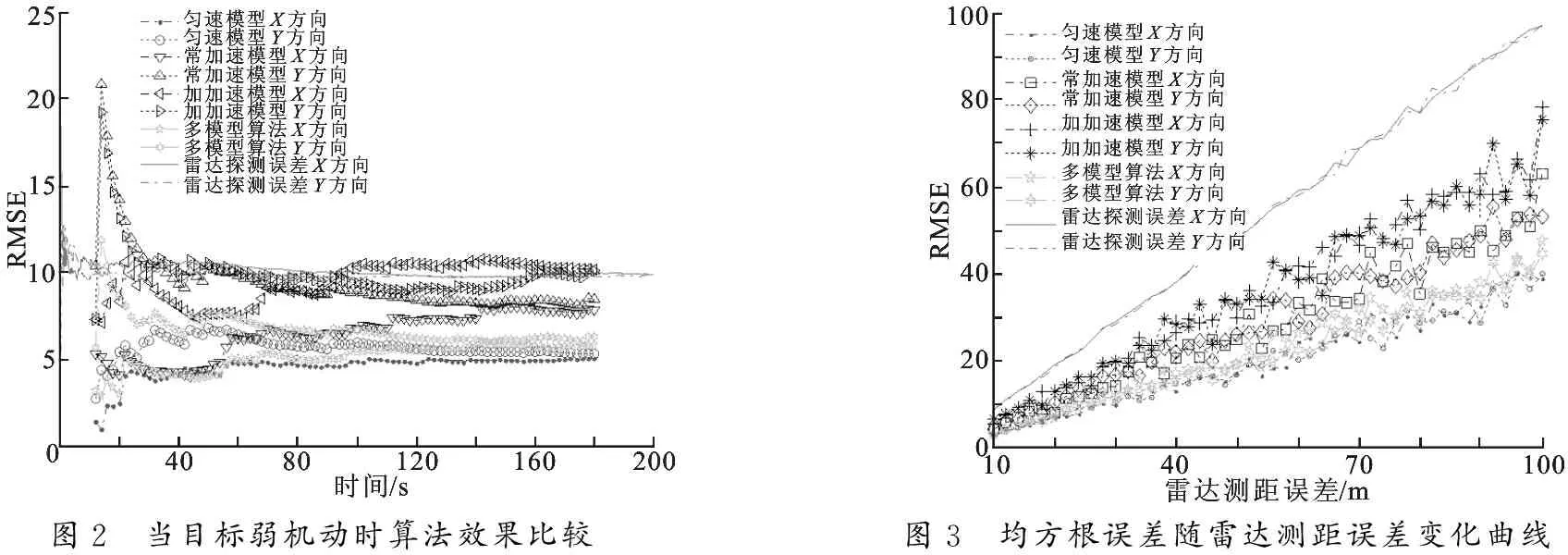
图2 当目标弱机动时算法效果比较图3 均方根误差随雷达测距误差变化曲线

仿真2 假定雷达的采样周期为0.08 s，时间配准周期为1 s，雷达的测距误差由 10 m 至 100 m 变化，则多模型最小二乘时间配准算法的均方根误差随雷达测距误差情况如图3所示．

由图3可以看出，当雷达的探测误差增大时，3种模型的时间配准算法的误差随着探测误差也线性增大．匀速模型的时间配准效果保持最好，且匀速模型的配准误差增加速率最小，对误差的抑制效果最好．

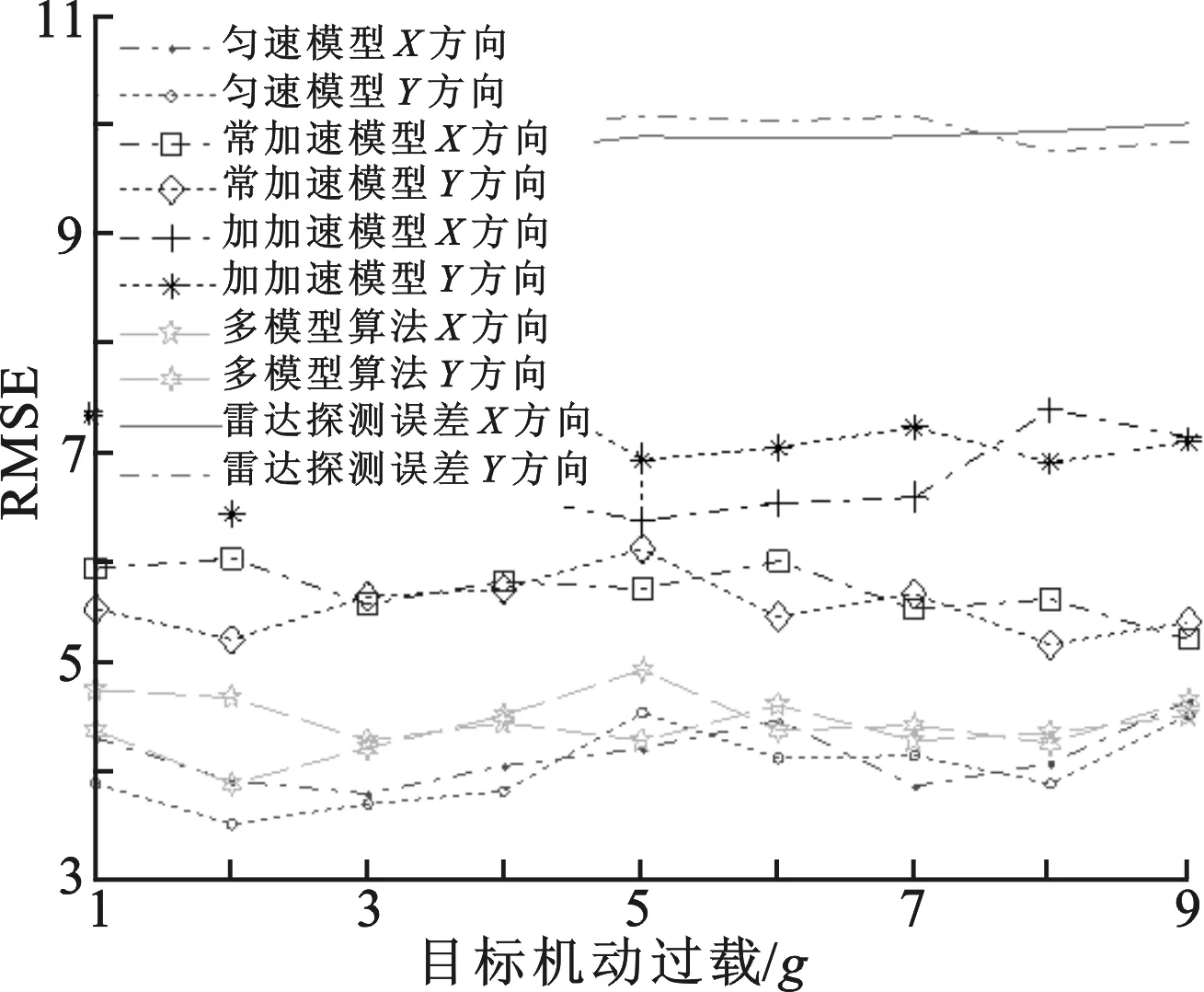
图4 均方根误差随目标机动过载变化曲线

仿真3 假定目标匀加速运动时的加速度从1g至9g变化．雷达采样周期为 0.08 s，时间配准周期为 1 s，雷达测距误差为 10 m，则多模型最小二乘时间配准算法的均方根误差随目标机动过载的变化情况如图4所示．

由图4可以看出，3种模型的时间配准误差不随目标机动的过载增大而增大，匀速模型的时间配准均方根误差保持在5上下，匀加速模型的时间配准均方根误差保持在8上下，加加速模型的时间配准均方根误差保持在10上下．因此，当目标直线运动时，多模型最小二乘时间配准算法的均方根误差不受目标机动过载的影响．

2.2 目标为强机动状态

假定目标在0～20 s为匀速直线运动；在20～50 s为匀加速直线运动，加速度为5g；在 50～ 80 s 为匀速圆周运动；在 80～ 200 s 为匀加速圆周运动，加速度为 6g，圆周运动的半径为 3 000 m．目标的初始位置为(100，3 000)，初始速度为 420 m/s，初始速度倾角为 π/4．在10～ 180 s 内进行时间配准．

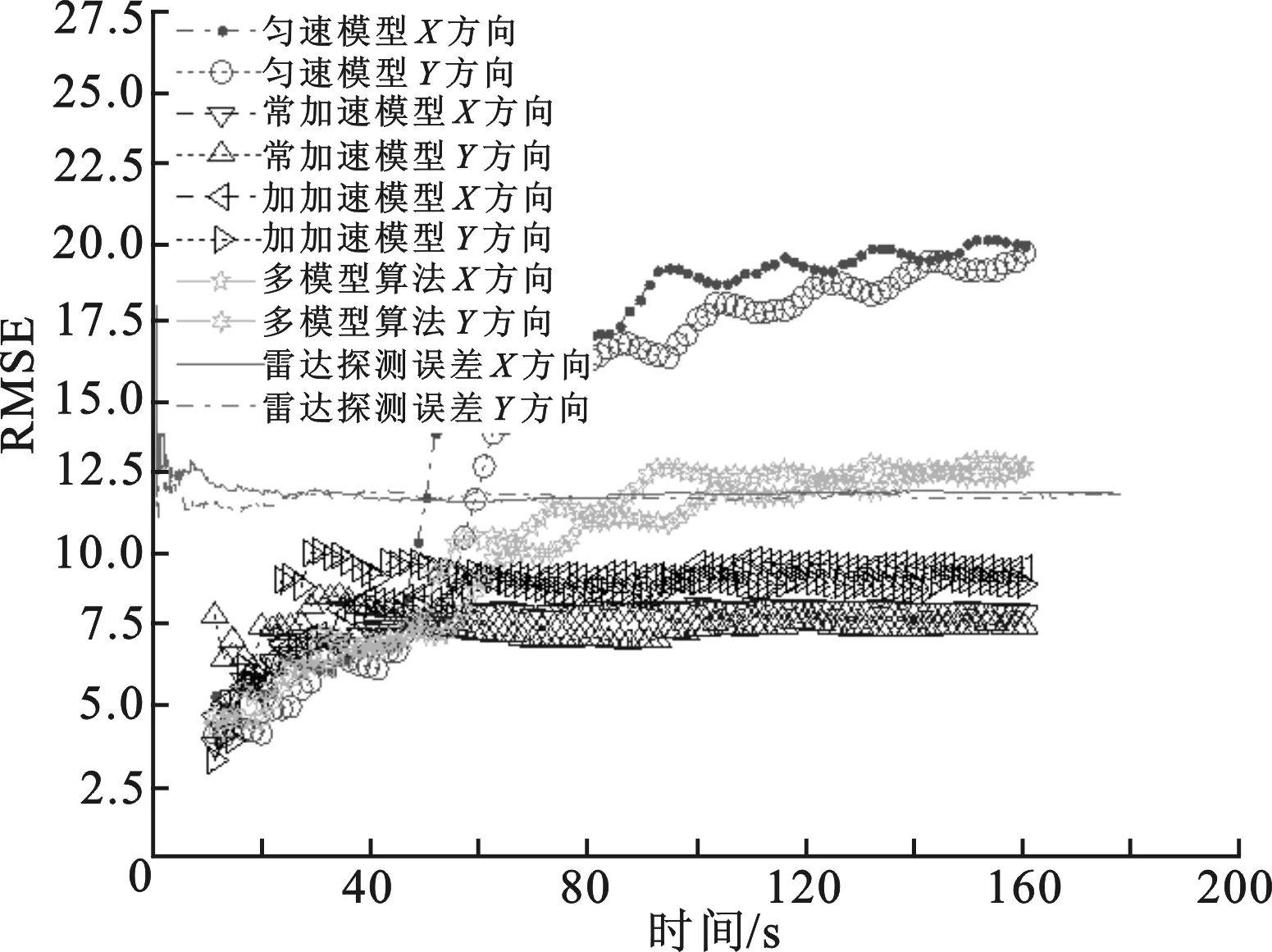
图5 均方根误差随时间变化曲线

仿真4 雷达传感器的采样周期为0.08 s，配准周期为1 s，雷达的测距误差为 10 m，则多模型最小二乘时间配准算法的均方根误差如图5所示．

由图5可以看出，在10～50 s阶段，目标为直线运动，匀速模型的时间配准误差依然最小．但是在 50 s 以后，目标进行圆周运动，匀速模型的时间配准误差迅速增大，最终在20上下震荡；而常加速模型和加加速模型的时间配准算法的均方根误差一直在7上下．多模型最小二乘时间配准算法的均方根误差在圆周运动阶段虽然有所增大，但是也没有剧烈的恶化．

仿真5 假定雷达传感器的采样周期为0.08 s，配准周期为 1 s，雷达的测距误差由 10 m 至 100 m 变化，则多模型最小二乘时间配准算法的均方根误差随雷达测距误差情况如图6所示．

由图6可以看出，在雷达探测误差小于30 m时，匀速模型时间配准算法的均方根误差最大，常加速模型时间配准算法的均方根误差最小；当雷达探测误差大于 60 m 时，匀速模型时间配准算法的均方根误差最小，加加速模型时间配准算法的均方根误差最大．无论雷达的探测误差如何变化，多模型最小二乘时间配准算法的均方根误差均保持在一个较小的水平． 因此， 多模型最小二乘时间配准算法在目标为强机动的情况下， 其优越性不受雷达探测误差的影响．

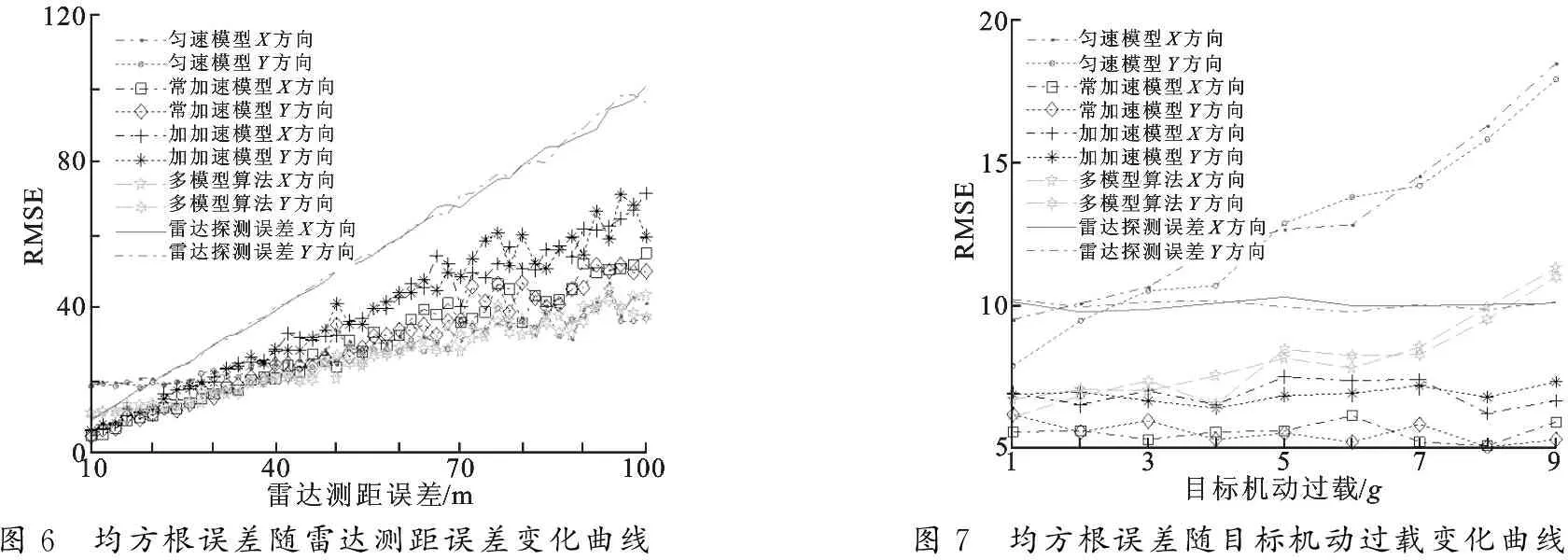
图6 均方根误差随雷达测距误差变化曲线图7 均方根误差随目标机动过载变化曲线

仿真6 假定目标匀加速运动时的加速度从1g至9g变化．雷达采样周期率为 0.08 s，时间配准周期为 1 s，雷达测距误差为 10 m，则多模型最小二乘时间配准算法的均方根误差随目标机动过载的变化情况如图7所示．

由图7可以看出，当目标圆周运动的机动过载小于3g时，匀速模型的时间配准算法均方根误差仍然和雷达的探测误差相当；如果目标的机动过载继续增大，匀速模型的时间配准均方根误差急剧恶化，远大于雷达的探测误差．常加速模型和加加速模型的时间配准均方根误差不随目标机动过载的增大而增大，保持在平稳状态．多模型最小二乘时间配准算法的配准均方根误差在目标机动过载为9g时依然为超过雷达的探测误差，因此，目标的机动过载较大时，多模型最小二乘时间配准算法的均方根误差均保持在一个较小的水平．

由以上两组仿真可以看出，当目标弱机动时，匀速模型的时间配准算法取得较好效果．当目标强机动时，若雷达探测误差小于 30 m，则加加速模型时间配准取得较好效果；若雷达探测误差大于 30 m，则常加速模型和匀加速模型取得较好效果．而笔者提出的多模型最小二乘时间配准算法虽不能取得最佳的时间配准结果，但是无论目标为何种机动，雷达探测精度如何，配准结果的X方向与Y方向的均方根误差一直保持较低水平，且不发散，结果均值得信赖．

3 总 结

针对传统最小二乘时间配准算法的不足，结合多模型的思想，在推导了常加速模型、加加速模型时间配准算法的基础上，笔者提出了多模型最小二乘时间配准算法．而且笔者所研究的多模型最小二乘可应用于时间配准周期与雷达采样周期之比为非整数的情况．通过大量仿真，验证了多模型最小二乘时间配准算法在目标机动过载从 1g至 9g变化时保持算法的有效性，在雷达的探测误差从 10 m 至 100 m 变化时也保持算法的有效性．

[1] 胡国平, 张守宏. 多传感器协同探测目标的分类识别研究[J]. 西安电子科技大学学报, 2009, 36(3): 443-447.

Hu Guoping, Zhang Shouhong. Study of Target Recognition Based on Multi-sensor Cooperating with Exploration[J]. Journal of Xidian University, 2009, 36(3): 443-447.

[2] 韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M]. 北京: 清华大学出版社, 2006.

[3] 王宝树, 李芳社. 基于数据融合技术的多目标跟踪算法研究[J]. 西安电子科技大学学报, 1998, 25(3): 269-272.

Wang Baoshu, Li Fangshe. Multi Target Tracking Algorithm Base on Data Fusion[J]. Journal of Xidian University, 1998, 25(3): 269-272..

[4] Li W, Leung H, Zhou Yifeng. Space-time Registration of Radar and ESM Using Unscented Kalman Filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 824-836.

[5] 潘自凯, 董文锋, 王正国. 基于曲线拟合的PRS/IRS时间对准方法研究[J]. 空军雷达学院学报, 2011, 25(5): 343-346.

Pan Zikai, Dong Wenfeng, Wang Zhengguo. Study on PRS/IRS Time Registration Based on Curve Fitting[J]. Journal of Air Force Radar Academy, 2011, 25(5): 343-346.

[6] 李林, 黄柯棣, 何芳. 集中式多传感器融合系统中的时间配准研究[J]. 传感技术学报, 2007, 20(11): 2445-2449.

Li Lin, Huang Kedi, He Fang. Research on Time Alignment Algorithms of Centralized Multi-Sensor Fusion System[J]. Chinese Journal of Sesors and Actuators, 2007, 20(11): 2445-2449.

[7] Fortunati S, Farina A. Least Squares Estimation and Cramér-Rao Type Lower Bounds for Relative Sensor Registration Process[J]. IEEE Transactions on Signal Processing, 2011, 59(3): 1075-1087.

[8] Huang X, Wu Q. The Method of Multi-sensor Time Registration[C]//Proceedings of International Conference on Electric Information and Control Engineering. Piscataway: IEEE, 2011: 6268-6271.

[9] 袁赣南, 袁克非, 张红伟, 等. 基于分段重叠的时间配准方法[J]. 传感器与微系统, 2012, 31(8): 48-51.

Yuan Gannan, Yuan Kefei, Zhang Hongwei, et al. Time Registration Method Based on Segmentation Overlap[J]. Transducer and Microsystem Technologies, 2012, 31(8): 48-51.

[10] Yang Wenjing, Cui Fan, Li Xun, et al. Research on Time Registration Algorithms of Multi-sensor Fusion System[C]//Proceedings of International Conference on Computer Science and Automation Engineering. Piscataway: IEEE, 2011: 446-449.

[11] Blair W D, Rice T R, Alouani A T, et al. Asynchronous Data Fusion for Target Tracking with a Multitasking Radar and Optical Sensor[C]//Proceedings of the SPIE Conference on Acquisition, Tracking, and Pointing: V. Bellingham: SPIE, 1991: 234-245.