S3PR网的严格极小信标计算方法

尤 丹， 刘 苗， 吴文慧， 王寿光

(1. 浙江工商大学 信息与电子工程学院，浙江 杭州 310018；2. 西安电子科技大学 机电工程学院，陕西 西安 710071)

作为一个数学建模工具，Petri[1]网能够描述资源共享、冲突、互斥、并发和不确定性，而且能帮助研究者发现系统潜在的死锁，并使用相应的控制策略来防止死锁，因而被广泛地应用于柔性制造系统死锁的分析与控制．在众多Petri 模型中，S3PR 网[2]是学者们研究柔性制造系统死锁问题时较常用的模型．目前许多学者致力于极小信标相关理论的研究[3-8]，并提出了计算极小信标的算法，但这些算法的计算效率不高．现今，基于信标的死锁控制问题[9-10]，针对普通Petri网比较成熟，但相对较为复杂的一般Petri网而言，信标研究还处于初期阶段．资源环法是目前计算S3PR 网严格极小信标最有效的方法之一．针对S3PR 网，文献[5]提出了基于计算资源环的算法并提出环资源子集的概念以克服资源环法的不足．同时，还提出环资源子集的计算算法以及环资源子集对应的信标是严格极小信标的充分必要条件，在此基础上提出一种快速计算严格极小信标的算法．但是文献[5]没有分析S3PR网中一类特殊库所与严格极小信标的关系，笔者针对这类特殊库所进行研究，提出基于环资源计算严格极小信标的方法．由于该方法避免环资源子集特征资源子网[5]强连通的判断，所以与环资源子集法[5]相比，有更高的计算效率．

1 计算严格极小信标

Peri网、S3PR网以及资源环的基本定义和相关符号说明参见文献[1-2, 5]．

在这一部分，笔者针对S3PR网中一类特殊操作库所和特殊资源库所进行定义与分析．

在下面的讨论中，用Ω来表示S3PR网N=(PA∪P0∪PR，T，F)的一个资源子集，其中Ω= {r1，r2，…，rm}⊆PR(m≥2)．

定义1 令N=(PA∪P0∪PR，T，F)，是一个S3PR网，Ωi和Ωj是N的资源子集．称Ωi和Ωj是可组合的，当且仅当Ωi∩Ωj≠Ø，Ωi⊄Ωj，Ωj⊄Ωi．对资源子集Ωi和Ωj的组合操作“∘”定义如下:

(1) 若Ωi和Ωj是可组合的，则Ωi∘Ωj=Ωi∪Ωj;

(2) 若Ωi和Ωj是不可组合的，则Ωi∘Ωj=Ø．

在下面的讨论中，如果Ωi和Ωj是可组合的，用Ωi，j来表示Ωi∘Ωj．显然，Ωi∘Ωi=Ø．

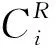
定义3 称资源子集Ω为组合环资源子集，如果∃Ω1，Ω2，…，Ωn∈Θ，使得Ω=Ω1∘Ω2∘ …∘Ωn=Ω1∪Ω2∪ …∪Ωn(n≥2)．用Ξ表示N中所有组合环资源子集的集合．

由定义2和定义3得到以下定理．

定理1 在S3PR网N中，∀Ω∈，Ω∪(·Ω∩Ω·)从N中导出的子网是强连通的．

定理2 令N=(PA∪P0∪PR，T，F)，是一个S3PR网，Ω= {r1，r2，…，rm}⊆PR(m≥2) ，是N的资源子集，则SΩ=Ω∪A(·ΩΩ·)，是一个信标[5]．

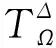
定理3SΩ是严格极小信标SMS当且仅当Ω是环资源子集，且它的特征资源子网NΩ是强连通的[5]．

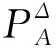
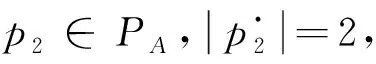
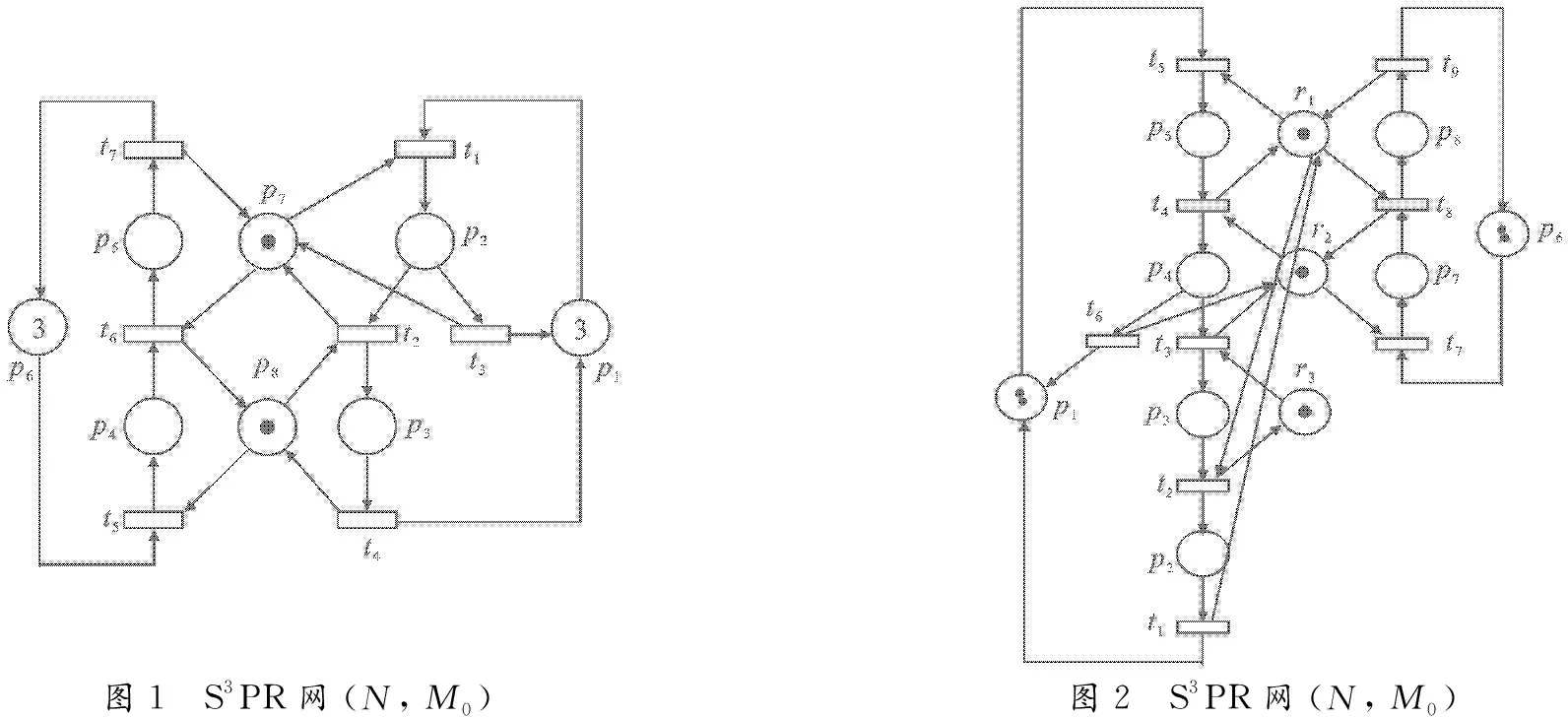
图1 S3PR网(N, M0)图2 S3PR网(N, M0)

推论1 若Ω是L-S3PR网N的环资源子集，则SΩ=Ω∪A(·ΩΩ·) 是严格极小信标SMS．

证明 在L-S3PR中，不存在特殊操作库所，同样也不存在特殊资源库所，由引理1或定理4即可得出此推论．

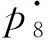
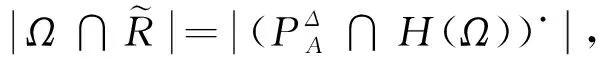
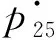
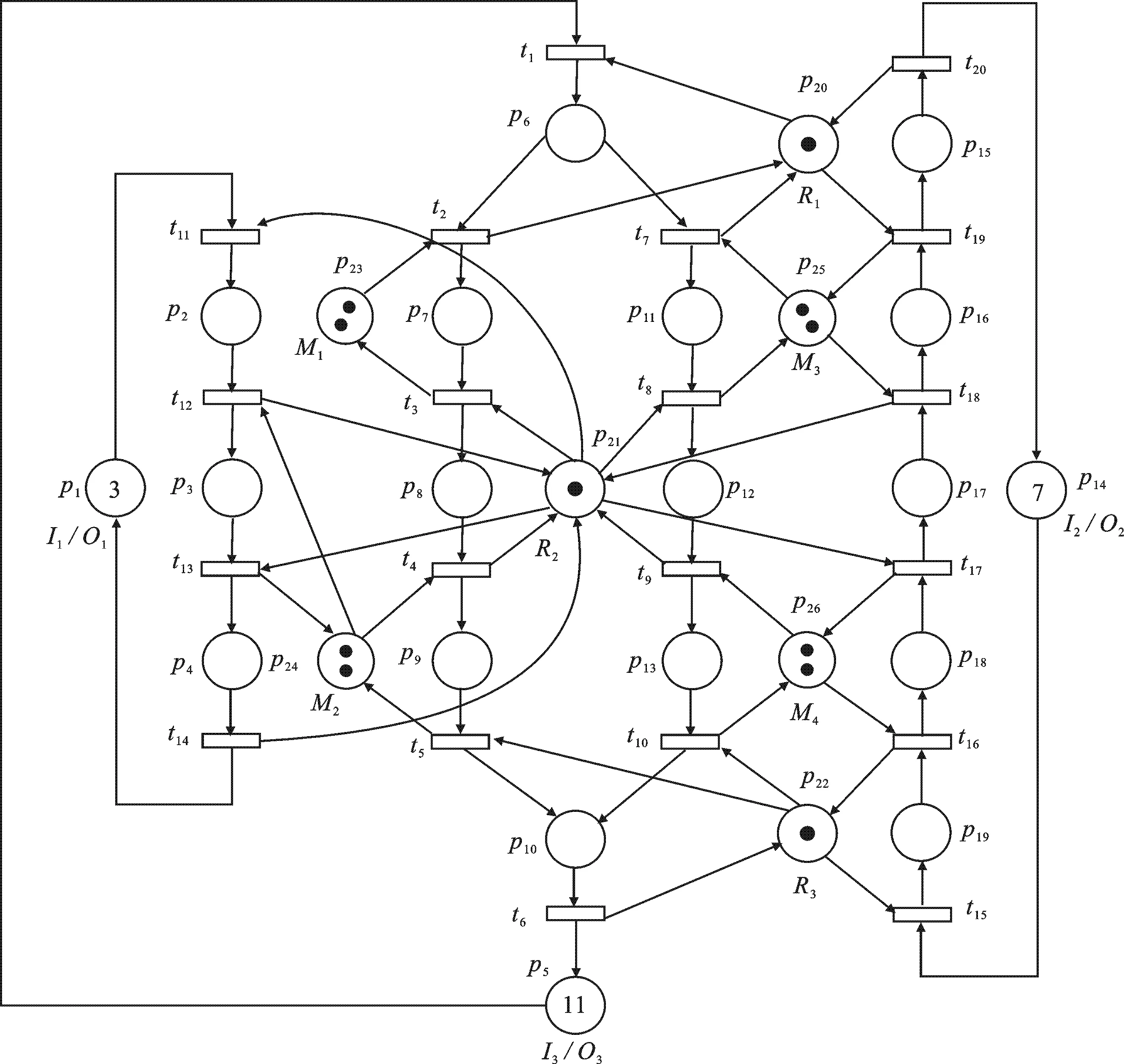
图3 一个柔性制造系统的Petri网模型

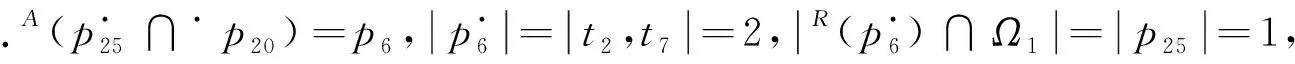
2 实验结果

下面用一个经典的柔性制造系统实例[2]来说明通过特殊库所判断严格极小信标的应用．图3为该柔性制造系统的S3PR网模型．

图3的简单环资源子集如表1所示，组合环资源子集如表2所示．图3共有25个环资源子集，这些环资源子集对应25个信标，但其中有些信标可能不是严格极小的．下面通过定理4～6来判断信标是否为严格极小信标．

表1 图3中的简单环资源子集

根据定义6～8，可知图3中操作库所p6是特殊操作库所，资源库所p20是特殊资源库所，资源库所p23、p25是特殊资源库所p20的特殊输入资源库所．

根据定理4可得，简单环资源子集Ω2，Ω4，Ω5，Ω6和组合环资源子集Ω2，4，Ω2，5，Ω4，5，Ω5，6，Ω2，4，5，Ω2，5，6，Ω4，5，6，Ω2，4，5，6所形成的信标中不包含任何特殊资源库所p20，则这些环资源子集一定可以形成严格极小信标SMS．

根据定理5可得，简单环资源子集Ω3和组合环资源子集Ω3，4，Ω3，5，Ω3，4，5，Ω3，5，6，Ω3，4，5，6所形成的信标中包含所有特殊输入资源库所p23和p25，则这些环资源子集一定可以形成严格极小信标SMS．

根据定理6可得，简单环资源子集Ω1和组合环资源子集Ω1，2，Ω1，2，4，Ω1，2，5，Ω1，2，4，5，Ω1，2，5，6，Ω1，2，4，5，6所形成的信标中包含一个特殊输入资源库所p23或p25，则这些环资源子集一定不可以形成严格极小信标SMS．

综上所述，可求出图3所有的严格极小信标，共18个．

表2 图3中的组合环资源子集

3 结 束 语

对于S3PR网，笔者首先定义了特殊操作库所和特殊资源库所，通过对其分析，提出通过特殊库所判定信标是否为严格极小信标的判定定理，基于判定定理有效求解出严格极小信标．实验结果表明，采用笔者所提出的方法，可以快速地计算出S3PR网中的严格极小信标．与文献[5]提出的方法相比，笔者提出的基于特殊库所求解严格极小信标的方法避免了对环资源子集特征资源子网是否是强连通的判断，进而也避免了通过资源子集求其特征资源子网．因此笔者提出的方法将提高计算效率．由于该方法只适用于一类S3PR网，把该方法应用到更大类型网将是以后研究的方向．

[1] Murata T. Petri Nets: Properties, Analysis, and Applications[J]. Proceeding of the IEEE, 1989, 77(4): 541-580.

[2] Ezpeleta J, Colom J M, Martinez J. A Petri Net Based Deadlock Prevention Policy for Flexible Manufacturing Systems[J]. IEEE Transactions on Robotics and Automation, 1995, 11(2): 173-184.

[3] 王安荣, 李志武. 基本信标计算的一种快速算法[J]. 西安电子科技大学学报, 2008, 35(4): 632-638.

Wang Anrong, Li Zhiwu. Effective Algorithm for Obtaining a Set of Elementary Siphons[J]. Journal of Xidian University, 2008, 35(4): 632-638.

[4] Wang Shouguang, Zhou Mengchu, Wang Chengying. Extracting All Minimal Siphons from Maximal Unmarked Siphons in Manufacturing-oriented Petri Nets [C]//IEEE International Conference on Automation Science and Engineering. Piscataway: IEEE, 2011: 399-404.

[5] Wang Shouguang, Wang Chengying, Zhou Mengchu. A Method to Compute Strict Minimal Siphons in S3PR Based on Loop Resource Subsets [J]. IEEE Transactions on Systems, Man, and Cybernetics Systems, 2012, 42(1): 226-237.

[6] Wang Shouguang, Li Yue, Wang Chengying, et al. Computation of All Minimal Siphons in Petri Nets[C]//Proceedings of 9th IEEE Conference on Networking, Sensing and Control. Piscataway: IEEE, 2012: 4651

[7] Liu Xiangling, Wang Anrong, Li Zhiwu. A Fast Algorithm to Find a Set of Elementary Siphons for a Class of Petri Nets[C]//Proceedings of IEEE International Conference on Automation Science and Engineering. Piscataway: IEEE, 2006: 399-404.

[8] Xing Keyi, Zhou Mengchu, Wang Feng, et al. Resource Transition Circuits and Siphons for Deadlock Control of Automated Manufacturing Systems[J]. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 2011, 41(1): 74-84.

[9] Li Zhiwu, Zhou Mengchu. Control of Elementary and Dependent Siphons in Petri Nets and Their Application[J]. IEEE Transactions on System, Man, and Cybernetics Part A: Systems and Humans, 2008, 38(1): 133-148.

[10] Li Zhiwu, Zhao Mi. On Controllability of Dependent Siphons for Deadlock Prevention in Generalized Petri Nets [J]. IEEE Transactions on Systems, Man, and Cybernetics Part A: Systems and Humans, 2008, 38(2): 369-384.