覆盖网络中多服务静态部署算法

脱立恒， 倪 宏， 李满天， 刘 学

(1. 中国科学院大学 理学院，北京 100049；2. 中国科学院声学研究所 国家网络新媒体工程技术研究中心，北京 100190)

随着网络和通信技术的进步和发展，互联网上出现了一大批新型网络应用，如网络会议、网络电视、社交网络等，相比传统的网页冲浪、文件传输等应用，新型应用的特点是应用服务器与用户的交互性更强，内容数据容量更大，内容的实时性要求更高．但现有的网络基础架构采用简单的端到端的设计原则，各路由节点单纯实现数据包的存储和转发，虽然在一定程度上这种简单的设计原则健壮性高、扩展性好、易于实现，但是越来越不能满足当前新型业务的发展需求．

内容网络[1]的研究就是为了解决现有网络体系架构的不足，它通过在现有的互联网上部署服务节点，使用应用层协议将这些服务节点构建成一个存在于IP网络之上的覆盖网络，从而实现为新型应用提供协同服务．通过将服务部署在覆盖网的各服务节点上，可以增加网络的灵活性，提高应用的响应时间，增强用户的使用体验，改善骨干核心网的拥塞问题．覆盖网络中的服务部署一直是一个热点研究问题，国内外许多研究者对该问题进行了研究．服务节点部署属于选址问题，选址问题模型分为3类：基于确定信息的节点部署模型[2]，基于概率模型的节点部署模型[3]和基于博弈论的节点部署模型[4-5]．Guha等从分层网络设计出发，以部署成本和层间路由成本最小化为优化目标，提出一种分层服务部署模型[6]．Laoutaris等研究了大规模内容分发网络(Content Deliver Network，CDN)的服务节点部署问题，提出了分布式的无容量约束K中值和无容量约束节点选址等两种模型[7]．Cahill等提出了一个针对流媒体服务部署问题的优化模型，优化目标为用户到服务器的连接成本和服务器的存储成本的组合[8]．另外，一些研究者针对云平台上的虚拟设施部署，同样给出了多种解决方法[9-11]，云平台上的虚拟设施同样是服务部署的实例化．Kecskemeti等提出了一种针对虚拟设备分布的服务部署方法，该方法以降低虚拟设备分布开销为目标[9]．郭涛等提出了云平台下一种虚拟机的个性化部署机制，该机制通过时间序列预测机制对宿主机的负载进行预测，进而实现虚拟设施部署[10]．

以上研究都是基于一定的覆盖网络拓扑结构或云平台结构，针对具体应用或虚拟设施的需求，设定不同的优化目标模型，其局限性是模型都针对单一服务，没有考虑多种服务共存的部署问题．陈香兰等研究了组合服务中的多服务静态部署问题[11]，针对基于因特网的服务系统，不考虑节点间的拓扑结构，提出了基础服务静态部署的最优化模型，在保证服务负载均衡分配以及服务请求传递的通信流量最小化的约束下，最优化服务部署的规模．但该研究成果只能针对基于Intranet的企业级应用，应用面狭窄．

综上，笔者考虑的应用场景是在广域网络的覆盖层上的多服务静态部署问题，不同于Intranet环境的研究，各服务节点间的通信时延开销将大幅影响用户的应用体验，多服务的特性也使得它有别于以上讨论中涉及的单一服务部署问题．因此，笔者提出了一种新的多服务部署模型，综合考虑了服务部署规模和用户的服务响应时间两方面的需求，给出了启发式的求解算法．

1 多服务静态部署模型

1.1 部署模型描述

考虑一个广域网环境中的覆盖网络，令N为网络中的服务节点数目，服务节点集合L= {l1，l2，…，lN}，节点可能是同构的，也可能是异构的，节点间通过底层的物理网络互连．系统中每个服务节点都可以部署多个服务，并且任意一个服务都可以完整地在任一节点上执行．设K为服务的种类数．服务集合S= {s1，s2，…，sK}，实际服务部署问题即为生成N个满足条件的Sj的集合．

(1)

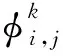
(2)

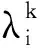
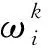
(3)

由服务请求分配矩阵，可以得到服务部署规模的定义，设节点i上的服务副本的个数为节点i的服务部署规模，可以由服务请求分配矩阵得到服务部署矩阵，即

(7)

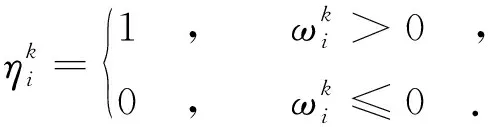
整个系统的服务部署规模为各节点服务规模之和，可表示为

(8)

显然，最大的服务部署规模为在每一个节点上部署所有K个服务，即Mmax=KN．

1.2 资源限制

网络应用服务系统中响应时间是用户服务质量最重要的参数．服务响应时间通常包括通信延迟和服务处理延迟，当服务系统存在请求转发时，服务响应时间还包括请求转发延迟，这里重点研究请求转发延迟．假设任意两个服务节点间的通信延迟用转发延迟矩阵表示为

(9)

其中，ti，j表示节点i与节点j间的通信时延，可以用跳数表示，也可以用实际时延表示．假设任意两个节点请求，经过第3个节点的转发后的通信时延均比两个节点直接转发通信时延要大(该条件可由底层物理网络路由保证)，即满足

tp(1)，p(2)+tp(2)，p(3)>tp(1)，p(3)．

(10)

下面研究在平均请求转发时间满足服务质量要求时，如何使服务部署规模最小化．假设服务系统的平均请求转发延迟满足

(11)

其中，T为服务质量要求的最大请求转发延迟．

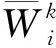
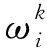
(12)

1.3 问题描述

综合以上定义，在请求转发延迟限制在一定范围之内，同时满足服务器的并发上限要求和最小化服务部署规模时，可以定义覆盖网络中的多服务静态部署问题模型(Static Multi-Service deployment Model， SMSPM)为

(13)

1.4 SMSPM模型分析

定理1 SMSPM问题是非确定性多项式时间(NP)完全问题．

证明 分两步证明SMSPM问题是NP完全的．先证明SMSPM是NP问题，再证SMSPM是NP难的．

步骤1 SMSPM问题是NP问题．给定一个带权重的图G=V，E，其中，顶点由n个服务器和m个用户构成．每个服务器有两个属性l和o，l表示服务器所属的服务节点，o表示服务器所能提供的服务．每个用户节点有两个属性分别为i和k，i节点是该用户转发开销为0的服务节点，k代表该用户请求的服务类型，将用户转发到服务节点时，其转发开销为．当i=l且k=o时，转发开销为0；当k=o且i≠l时，转发开销为ti，j；当k≠o时，转发开销为∞．每个服务节点的请求上限为．假设Tm是将所有用户(即请求)指派给服务节点后的平均转发延迟开销，验证SMSPM问题是NP完全问题即是在给定的指派中，是否存在平均转发延迟开销为Tm的方案．假设A是“非确定性图灵机”，A的输入为n个服务器构成的集合Sj，m个用户构成的集合U和总开销T的猜测函数f．非确定性图灵机的工作包括两步：A非确定性猜测可能的指派方案．函数f确认猜测的指派方案的平均转发延迟开销是否为Tm，若验证成功，则停止；否则，继续．因此，至少在给定一个用户到服务器的指派，验证该指派方案的平均转发延迟开销是否为Tm，即为将所有转发延迟开销相加后取平均，时间复杂度为O(n)，验证过程可以在多项式时间内确定．一旦用户指派方案确定后，服务的部署问题随之解决．因此，SMSPM问题是NP问题．

步骤2 SMSPM问题是NP难的．假设存在可求解SMSPM问题的多项式时间，可将上述问题简化后用以解决设施选址问题(Facility Location Problem，FLP)[13-14]．FLP将用户i的带宽需求设置为 band(i)，每个服务器设置带宽上限，SMSPM将服务器的并发上限抽象为FLP的带宽上限，将用户i到服务器的并发贡献抽象为FLP的带宽需求为band(i)，即SMSPM问题的 band(i)=1 ，用户到服务器的指派仅依赖于并发限制和转发延迟两个限制条件．因为FLP能用SMSPM的多项式时间算法在多项式时间内求解．文献[14]中证明FLP是NP难的，因此，SMSPM问题是NP完全问题．

2 启发式算法

2.1 算法思想

文中使用启发式算法对SMSPM问题进行求解，其核心思想是贪婪策略．假设在初始时，所有节点均部署所有服务，每次选择使得总的转发延迟开销最小的节点上的服务进行删除．步骤如下:

(1) 选中一个节点，计算删除其上任意一个服务所带来总的转发延迟开销增量，选择最小增量的服务，即为该节点删除服务的最小转发开销．

(2) 计算每个节点的最小转发延迟开销，选择所有节点中最小转发延迟开销的节点，作为N个节点中的最小转发延迟开销．

(3) 删除N个节点中最小转发开销的节点对应的服务．

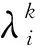
图1 请求分级转发

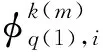
图2 请求转发重分配

2.2 算法复杂度分析

由于SMSPM模型分别从服务请求可以多次转发到不同节点和服务请求可以分流转发到多个节点等角度对实际问题进行抽象，其模型复杂，使用的启发式算法的复杂度也比较高．首先分析BND算法．BND算法先计算任意一个节点的请求转发最小延迟开销，共要计算N次；继续深入，选定1个节点后，计算该节点去掉任意一个服务所带来的最小延迟开销，共要计算K次．假如已经有其他节点 (N-1) 向该节点转发该服务，则要将该转发请求转发到其他节点上，同样是N-1 种可能，分配完该部分后，再计算将选定节点的选定服务请求转发到其他节点上，所以计算任意1个节点删除的1个服务算法复杂度为O(NK[(N-1)(N-1)+N])，由于每次删除1个服务，所以最多删除服务数即为NK，所有算法总的复杂度为O((NK)NK[(N-1)(N-1)+N])，即该算法的算法复杂度为O(N4K2)．BND算法是在多项式时间内可解的，但该算法算出的复杂度是算法的最大上限．实际中，当算法开始运行时，由于节点相互转发比较少，即公式 (N-1)(N-1) 很小，当算法运行到一定节点时，虽然转发情况增多，但由于服务的减少，(N-1)(N-1)、N和K的规模都在降低．同理，可以分析得到NBND算法的复杂度为O(N3K2)，由于NBND算法省去了转发的请求重新转发的步骤，每次转发1个请求后，再次选择服务时，其转发到其他节点数小于N，故实际NBND算法比BND算法的复杂度低很多．

3 实验仿真分析

通过仿真对比了BND算法和NBND算法的运算结果．文中模拟了N=20，K=30 的服务系统，随机生成服务请求矩阵，每个节点每种服务的请求到达率控制在0～100，随机生成转发延迟矩阵，转发延迟范围控制在51～100，假设所有节点的最大服务上限均相同，并且要求初始状态时，节点所有服务的请求到达率之和小于服务器最大服务上限．系统每运行1次称为1次运行实例．1次运行实例包括随机生成1次服务请求矩阵，并分别通过BND算法和NBND算法求解服务部署和请求转发方案．

图3 部署规模对平均转发延迟开销的影响

模拟实验分别比较了两种启发式算法在求解SMSPM问题时的服务部署规模、平均转发延迟开销变化和算法复杂度变化．由于算法是从所有节点部署的所有服务开始的，当每次减少服务部署规模时，平均转发延迟开销与服务部署规模减少量的变化情况如图3所示．随着服务部署规模减少量的增大，请求转发延迟的开销不断增加．算法开始时，BND算法和NBND算法的平均转发开销随着服务部署规模的减少而相同增加转发延迟，但到达一定程度时，由于BND算法的回退步骤将之前的转发请求重新调整，因此，BND算法的平均转发开销比NBND算法的转发开销增加速度慢，在达到目标平均转发开销时，BND算法的规模减少量更大，即BND算法使得服务部署规模更小．图4给出了两种算法的循环次数对比，BND算法的回退算法更加复杂，随着服务部署规模的减小，其循环次数的增加越来越快．文中运行100次运行实例，将两种算法的服务部署规模进行了概率统计，概率密度如图5所示．BND算法的平均服务部署规模为246，NBND算法的平均服务部署规模为287，两种算法分别将服务部署规模降低了59%和52.2%．

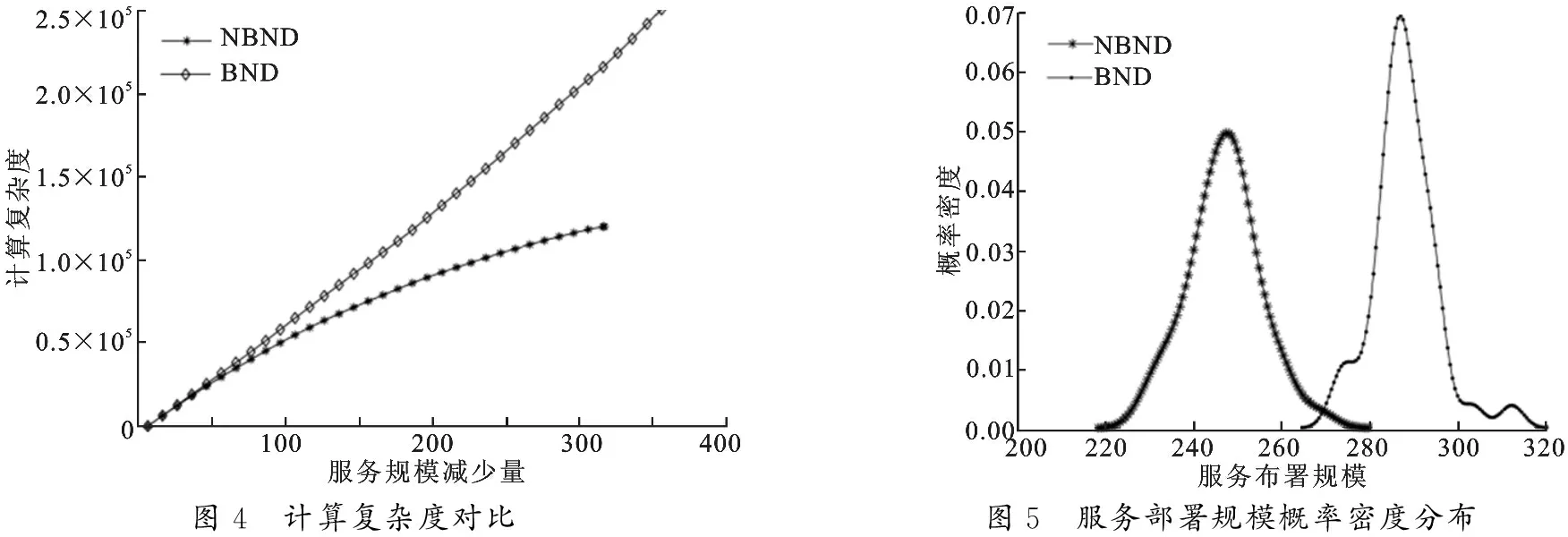
图4 计算复杂度对比图5 服务部署规模概率密度分布

4 结 束 语

研究了覆盖网络中多服务静态部署问题．在服务部署过程中考虑系统平均转发时间限制和服务节点的最大服务规模限制，定义了一种更加全面的问题模型——SMSPM，证明了SMSPM问题属于NP完全问题．给出了两种贪婪启发式算法BND和NBND，通过两种算法分别对SMSPM问题进行求解，并分析其时间复杂度．通过仿真，验证了SMSPM模型的有效性，BND和NBND两种算法将服务部署规模分别降低了59%和52.2%．对于NP完全问题，有多种近似算法，文中给出的启发式算法复杂度较高．接下来的研究工作是设计更加高效的近似算法．

[1] 尹浩, 袁小群, 林闯, 等. 内容网络服务节点部署理论综述[J]. 计算机学报, 2010, 33(9): 1161-1620.

Yin Hao, Yuan Xiaoqun, Lin Chuang, et al. The Survey of Service Nodes Deployment Theories for Content Networks[J]. Chinese Journal of Computers, 2010, 33(9): 1161-1620.

[2] Goldengorin B, Ghosh D, Sierksma G. Branch and PEG Algorithms for the Simple Plant Location Problem[J]. Computers & Operations Research, 2003, 30(7): 967-981.

[3] Brimberg J, Hansen P, Mladenovic N, et al. Improvement and Comparison of Heuristics for Solving the Uncapacitated Multisource Weber Problem[J]. Operations Research, 2000, 48(3): 444-460.

[4] Rosing K E. An Optimal Method for Solving the (Generalized) Multi-Weber Problem[J]. European Journal of Operational Research, 1992, 58(3): 414-426.

[5] Chekuri C, Chuzhoy J, Lewin-Eytan L, et al. Non-cooperative Multicast and Facility Location Games[C]//Proceedings of the 7th ACM Conference on Electronic Commerce. New York: ACM, 2006: 72-81.

[6] Guha S, Khuller S. Greedy Strikes Back: Improved Facility Location Algorithms[J]. Journal of Algorithms, 1999, 31(1): 228-248.

[7] Laoutaris N, Smaragdakis G, Oikonomou K, et al. Distributed Deployment of Service Facilities in Large-scale Networks[C]//Proceedings of the 26th IEEE International Conference on Computer Communications. Piscataway: IEEE, 2007: 2144-2152.

[8] Cahill A J, Sreenan C J. An Efficient CDN Deployment Algorithm for the Delivery of High-quality TV Content[C]//Proceedings of the 12th Annual ACM International Conference on Multimedia. New York: ACM, 2004: 975-976.

[9] Kecskemeti G, Terstyanszky G, Kacsuk P, et al. An Approach for Virtual Appliance Distribution for Service Deployment[J]. Future Generation Computer Systems, 2011, 27(3): 280-289.

[10] 郭涛, 温少君, 陈俊杰. 基于个性化的云平台虚拟机部署机制的研究[J]. 太原理工大学学报, 2012, 43(2): 125-129.

Guo Tao, Wen Shaojun, Chen Junjie. The Research on Personalized VM Deployment Mechanism in Cloud[J]. Journal of Taiyuan University of Technology, 2012, 43(2): 125-129.

[11] Liu T, Lu T, Wang W, et al. SDMS-O: a Service Deployment Management System for Optimization in Clouds While Guaranteeing Users’ QoS Requirements[J]. Future Generation Computer Systems, 2012, 28(7): 1100-1109.

[12] 陈香兰, 李曦, 龚育昌. 服务组合中一种静态基础服务部署研究[J]. 小型微型计算机系统, 2008, 29(4): 709-714.

Chen Xianglan, Li Xi, Gong Yuchang. Static Service Deployment Algorithm in Service Composition[J]. Journal of Chinese Computer Systems, 2008, 29(4): 709-714.

[13] 史佩昌, 王怀民, 尹刚, 等. 云服务传递网络资源动态分配模型[J]. 计算机学报, 2011, 34(12): 2305-2318.

Shi Peichang, Wang Huaimin, Yin Gang, et al. The Dynamic Allocation Model for the Resources of Cloud Services Delivery Network[J]. Chinese Journal of Computers, 2011, 34(12): 2305-2318.

[14] Averbakh I. Complexity of Robust Single Facility Location Problems on Networks with Uncertain Edge Lengths[J]. Discrete Applied Mathematics, 2003, 127(3): 505-522.