基于测试数据时间序列的导弹故障预测*

叶玮，郑守铎，温瑞珩

(中国人民解放军92941部队，辽宁 葫芦岛 125001)

0 引言

导弹故障预测是通过对导弹关键状态参数的变化进行趋势分析，并对导弹系统的未来行为进行推断，其目的是在故障发生前及早地实现故障预报，并由此针对性地采取措施预防、减缓故障的发生，将事故消灭在萌芽状态，从而最大限度地减小故障发生的可能和降低故障的危害[1]。由于导弹系统设备的使用寿命受加电时间的影响，在导弹服役期间，只能通过定期检验来判断导弹的性能状况，不能经常进行测试，因此不可能随时全面掌握导弹的性能状况。但是如果能通过对导弹测试数据进行分析处理来实现导弹在定期检查时性能变化趋势的预测，必将有助于全面掌握导弹的性能状况，进而提高导弹的战备保障能力。

1 时间序列趋势预测

时间序列预测是用被预测变量的历史信息预测未来值。时间序列预测的方法很多，主要有Box-Jcnkins模型、灰色预测法、神经网络模型、模糊理论、小波预测等趋势预测方法[2]。

灰色预测法用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型，预测未来某一时刻的特征量，或达到某一特征量的时间。灰色预测提供了在贫信息情况下求解系统问题的新途径，应用十分广泛，特别适用于序列较短且具有明显上升或明显下降趋势的时间序列预测[3]。

基于神经网络的预测方法近年来被人们普遍采用。神经网络是在现代生物学、人脑组织等研究所取得的成果基础上提出的, 一个三层神经网络可以任意精度逼近任何非线性连续函数，这为运用神经网络进行时间序列预测提供了数学保证[4]。同时，神经网络和其他理论(如模糊理论、遗传算法、粗糙集、模拟退火算法等)的结合研究也得到快速发展[5]。神经网络预测实现了非线性关系的隐式表达，容错性好，预测精度较高，动态自适应能力强，适合非线性复杂系统的智能预测[6]。

小波理论比较成熟的Mallat算法在预测中也经常被人们使用，但该算法不能满足时-频移(位)不变的要求，不能胜任实时递归预测的方法[7]。à Trous小波变换比较灵活，它可以把时间序列看作有序数据流的形式，在预测过程中逐步进行小波变换，还可以在变换过程中加入其他算法，如指数平滑处理、降噪处理等[8]。

自回归移动平均模型(auto regression moving average model,ARMA)可以说是迄今为止理论上最为完善的预测方法，它最初起源于市场经济预测，后来随着时序方法的发展及其应用领域的扩大，ARMA模型被成功用于工程系统的预测[9]。ARMA模型还有多元时间序列模型(ARMA vector model,ARMAV)、非平稳时间序列模型(auto regressive integrated moving average,ARIMA)、门限自回归模型(threshold auto regression,TAR)、指数自回归模型(exponent auto regression,EAR)等许多变种，分别适用于不同性质的时间序列[10]。

在导弹实际的测试过程中，参数测量的时间间隔并不一致，但是经过实际观察研究，在测试安排紧凑、时间间隔相差不大的情况下，实测值主要受加电次数的影响，而短期时间变化所造成的影响不明显。因此，可以从导弹测试的原始数据库中提取某参数的历史数据，组成相同时间间隔的历史数据时间序列。借助于SAS(statistical analysis system)预测技术，就可以挖掘导弹测试历史数据时间序列中的潜在规律，便于准确分析和预测导弹性能参数的变化。下面以导弹某一参数的实测数据(共85个观测值)为例，详细分析时间序列建模及优化过程，并运用组合模型进行导弹故障预测。数据观测值不进行罗列表示。

2 导弹故障预测建模

2.1 平稳性检查

将数据序列导入SAS数据库，以时间段(x)为时间编号(time ID),实测值字段(value)为变量(varible),作点线图，如图1所示。可以看出原序列有明显的线性趋势，带有不确定因素且不稳定。然后观察序列的相关性函数图，如图2所示。虽然该序列的偏自相关函数和逆自相关函数在滞后量大于1时大致截至为0，具有截尾性，但其自相关函数随滞后量的增加衰减缓慢，且在滞后量大于8之前的自相关函数值都在可信度范围以外。因此，可以判断该序列不是随机时间序列。在此判断基础上，进行序列的白噪声和稳定性测试可知，该序列的自相关系数不显著为0，不满足白噪声的条件；同时，单位根检验结果表明，ADF(augmented Dickey-Fuller)统计量的绝对值明显小于临界值的绝对值。显然，该序列为非平稳时间序列。综上所述，该序列带有明显的线性趋势，不满足随机时间序列条件，为确定性非平稳时间序列。

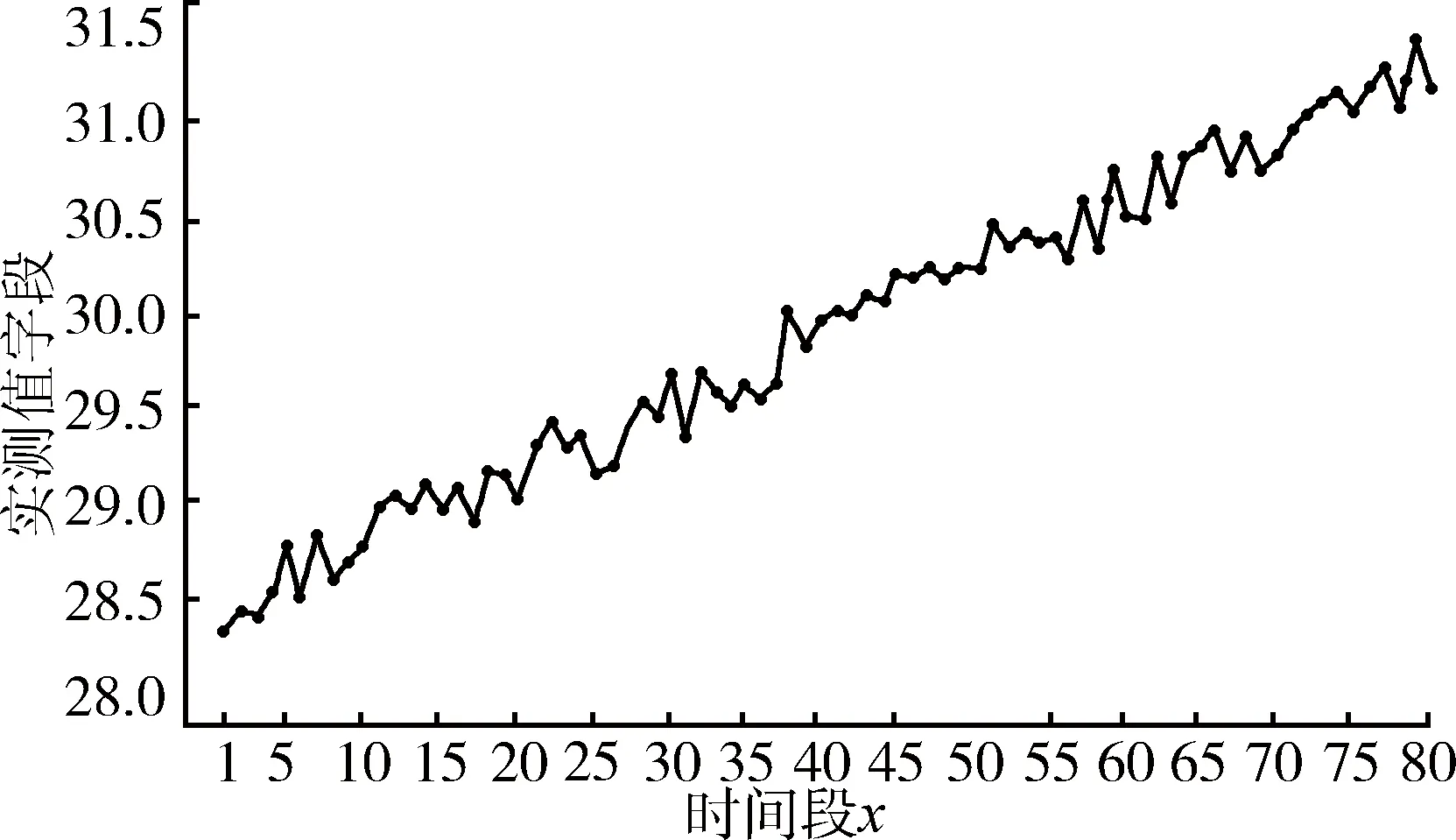
图1 原序列点线图Fig.1 Dot chart of primary series

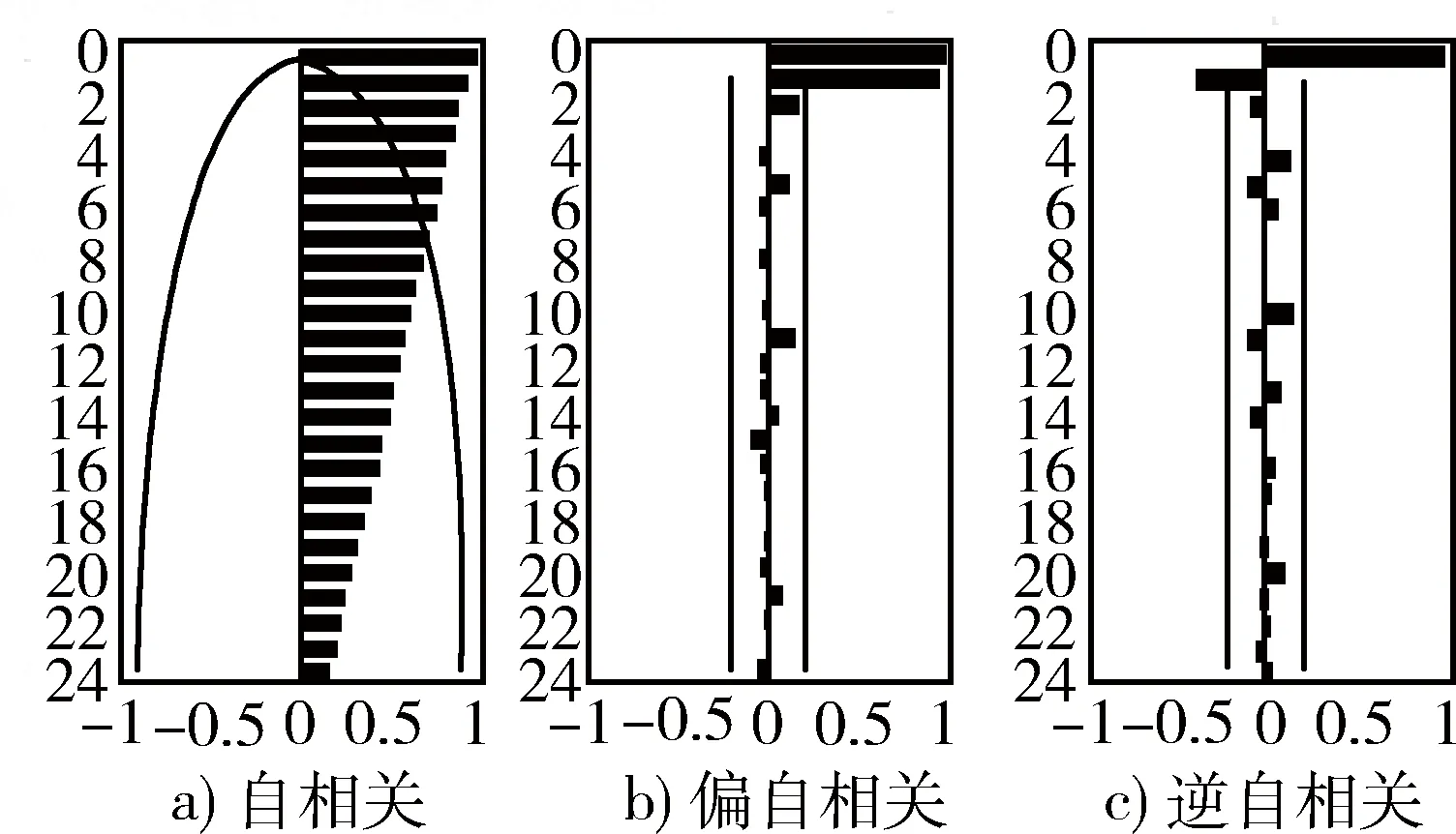
图2 原序列相关函数图Fig.2 Correlation function of primary series

2.2 趋势拟合

通过以上分析可知，该序列带有明显的线性趋势，因此对该序列进行线性拟合。由参数拟合统计量结果可确定趋势拟合为

μt=28.485 69+0.035t.

(1)

模型的T检验结果表明，常数项与自变量系数显著不为0，都有显著性意义；拟合模型残差平方和为1.040 48，均方误差仅为0.013 01，AIC(Akaike information ceiterion)统计量为-348.387 71，SBC(Schwartz Bayesian information ceiterion)统计量为-338.623 65，决定系数高达98.1%。显然，模型拟合良好。

2.3 残差序列平稳性检查

将残差序列数据导入SAS数据库，以时间字段(x)为时间编号(time ID)，残差值字段(y)为变量(varible)，作点线图观察，如图3所示。该残差序列值在0附近震荡，没有明显的确定性趋势，初步判定为随机时间序列。然后对该残差序列白噪声和单位根检验，如图4所示。可知该序列满足白噪声条件；同时，单位根检验结果表明，ADF统计量值明显大于临界值的绝对值。显然，该序列为随机平稳时间序列。

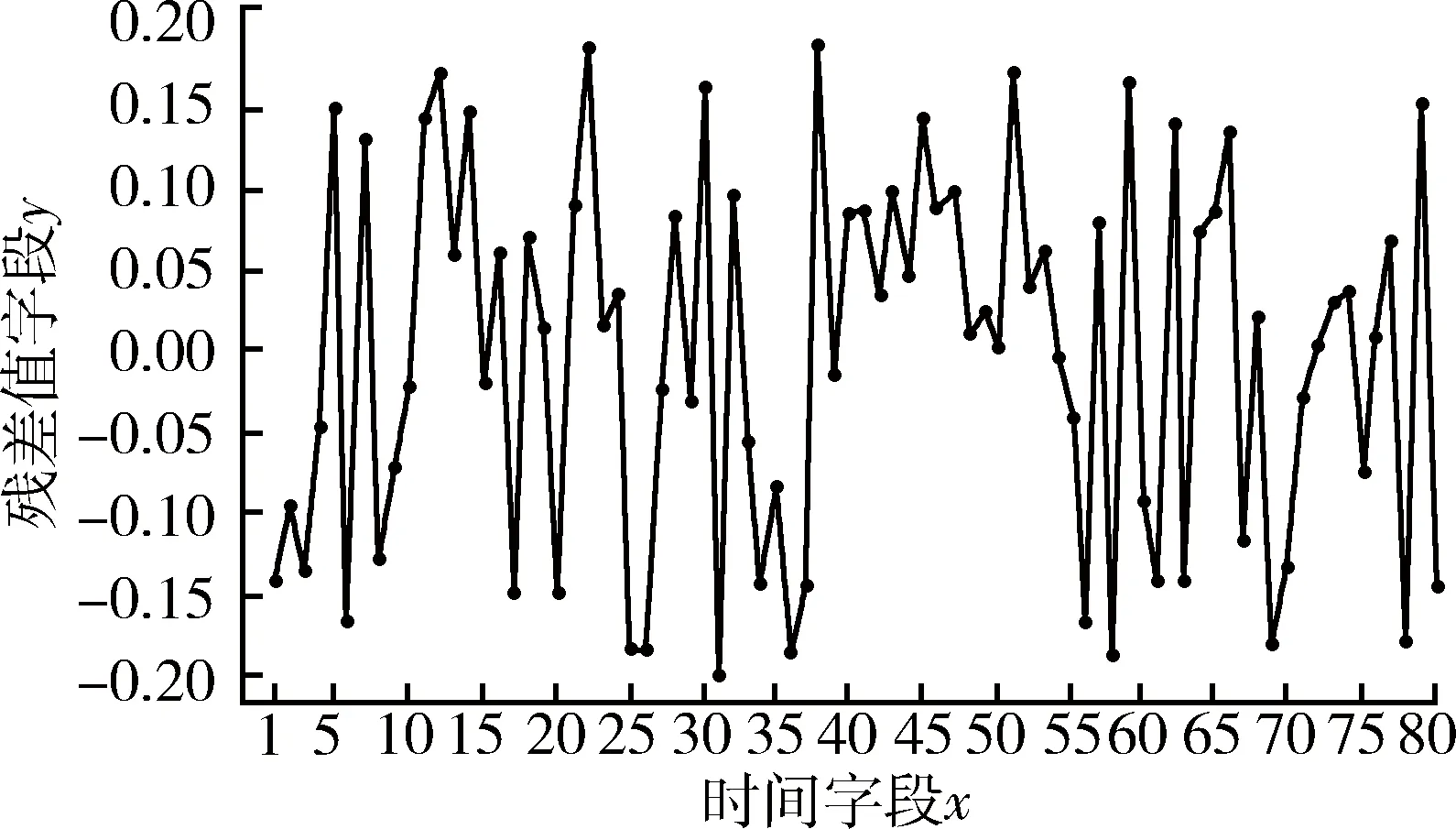
图3 拟合残差点线图Fig.3 Dot chart of fitting residual error

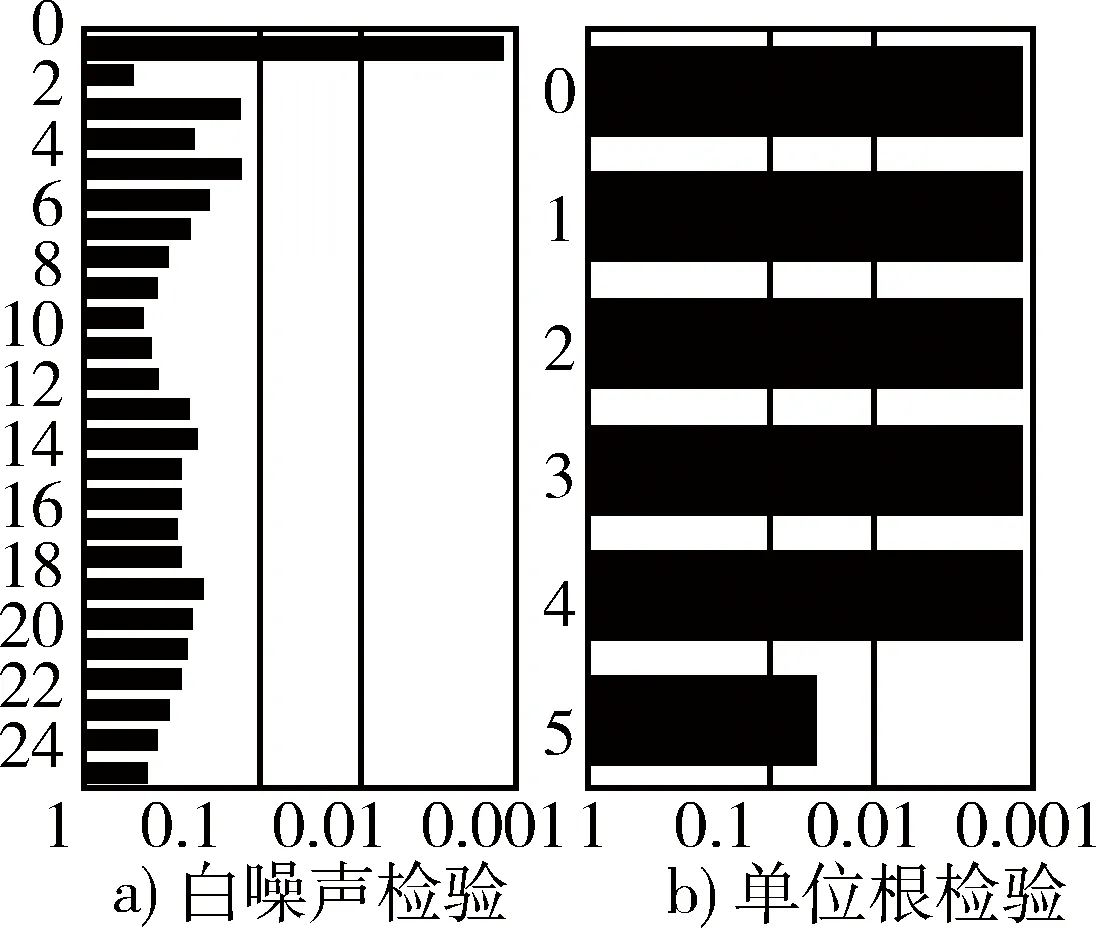
图4 拟合残差白噪声/单位根检验图Fig.4 White noise and unite root of fitting residual error

由该残差序列的相关性函数值可知，该残差序列除了延迟2阶的自相关系数在2倍标准差范围之外，其他阶数的自相关系数都在2倍标准差范围内波动。根据这个特点可以判断该序列具有短期相关性，进一步确定序列平稳。综上所述，该残差序列为随机平稳时间序列。

2.4 残差序列的识别及模型拟合

通过分析该残差序列的相关系数图(图5)，一方面，由于序列除了延迟2阶的自相关系数在2倍标准差范围之外，其他阶数的自相关系数都在2倍标准差范围内波动，可以认为该序列自相关系数2阶截尾，且由于偏自相关系数显示出一定的拖尾性，综合该序列自相关系数和偏自相关系数的性质，可以尝试使用MA(2)模型拟合该序列；另一方面，由于序列的自相关系数在延迟1，2，4阶等处均不显著为0，表现出一定的拖尾性，偏自相关系数在延迟2，4，6，13阶不显著为0，也表现出一定的拖尾性质，可以尝试使用ARMA模型拟合该序列。根据残差序列自相关系数和偏自相关系数中不显著为0的各个延迟阶数，构造相应的ARMA(p，d，q)模型，并对模型拟合结果进行整理，选择MA(2)模型来拟合该残差序列。

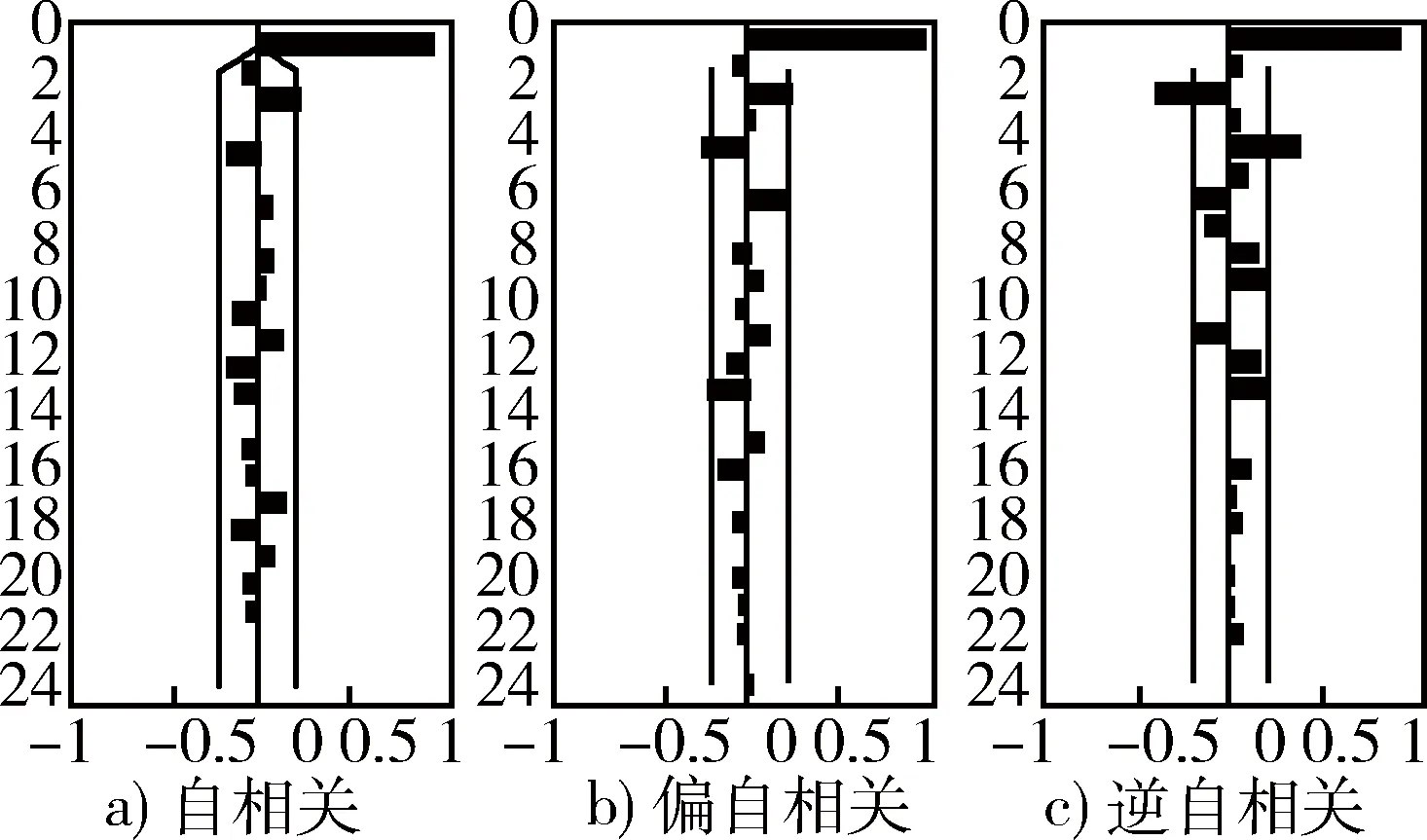
图5 拟合残差序列相关系数图Fig.5 Correlation coefficient chart of fitting residual error

在此基础上，首先对MA(2)模型进行模型检验。由拟合后的残差序列白噪声和单位根检验结果可知，残差序列白噪声检验中没有显著不为0的点，残差序列为白噪声序列，单位根检验结果表明，ADF统计量的绝对值明显大于临界值的绝对值，残差序列是平稳的。可见MA(2)模型对原残差序列的拟合较好。其次对MA(2)模型进行参数检验。由MA(2)模型的参数估计和检验结果值可知，lbθ2参数估计值显著不为0，而lgθ1参数参数估计值明显小于2倍标准差，T检验结果同时表明lgθ1不显著。因此，需要对模型进行优化。

由于MA(2)模型中不显著参数不是最高阶参数，需要计算θ1,θ2之间的相关系数。通过计算得θ1,θ2之间相关系数为0.003 5，表明参数之间的相关性很弱，因此可将MA(2)中的不显著参数θ1删去。优化后的MA(2)模型如下：

et=-0.499 29et-2.

(2)

对拟合模型后的残差序列进行进一步的分析，发现残差序列为白噪声随机序列，说明模型et=-0.499 29et-2比较合适。

2.5 组合模型

通过以上分析，得到组合模型为

μt=28.485 69+0.035t-0.499 29et-2.

(3)

组合模型拟合后的残差白噪声和单位根检验结果如图6所示。

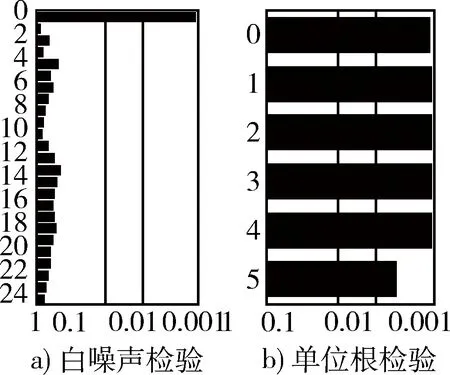
图6 组合模型拟合残差白噪声/单位根检验图Fig.6 White noise and unite root of fitting residual error of model

3 模型预测

利用组合模型对后5个数据进行预测，并与实际值比较。模型预测值与实际值对照表如表1所示。

从表1可看出，实际值与预测值相差很小，经检验2组的差值与0没有显著性差异。可以认为，该模型预测效果较好。

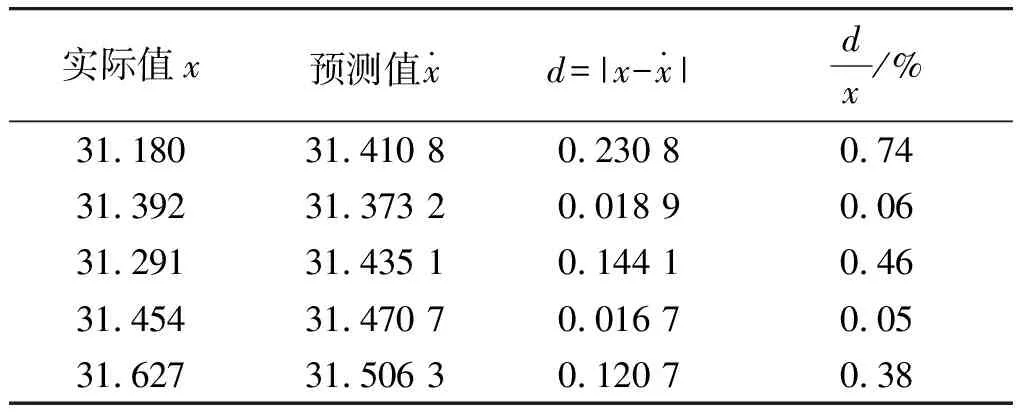
表1 模型预测值与实际值对照表Table 1 Contrast of forecast and factual value

以上使用的是点预测方法，在实际应用中，其预测结果的实用性和可靠性较差，因为未来发生的实际值几乎绝不可能等于点预测值，有时甚至偏差很大，这种不确定性有碍于对点预测结果的信任和使用。虽然没有一种预测方法能使预测结果同实际真值每次吻合，但是可以通过区间预测方法来划定一个预测范围，使它可能包含实际真值，并能预先确定包含真值的可能性大小。区间预测法的计算非常复杂，通常都采用统计软件来完成。运用组合模型和SAS软件对该序列进行置信水平为95%的区间预测。点线图如图7所示。

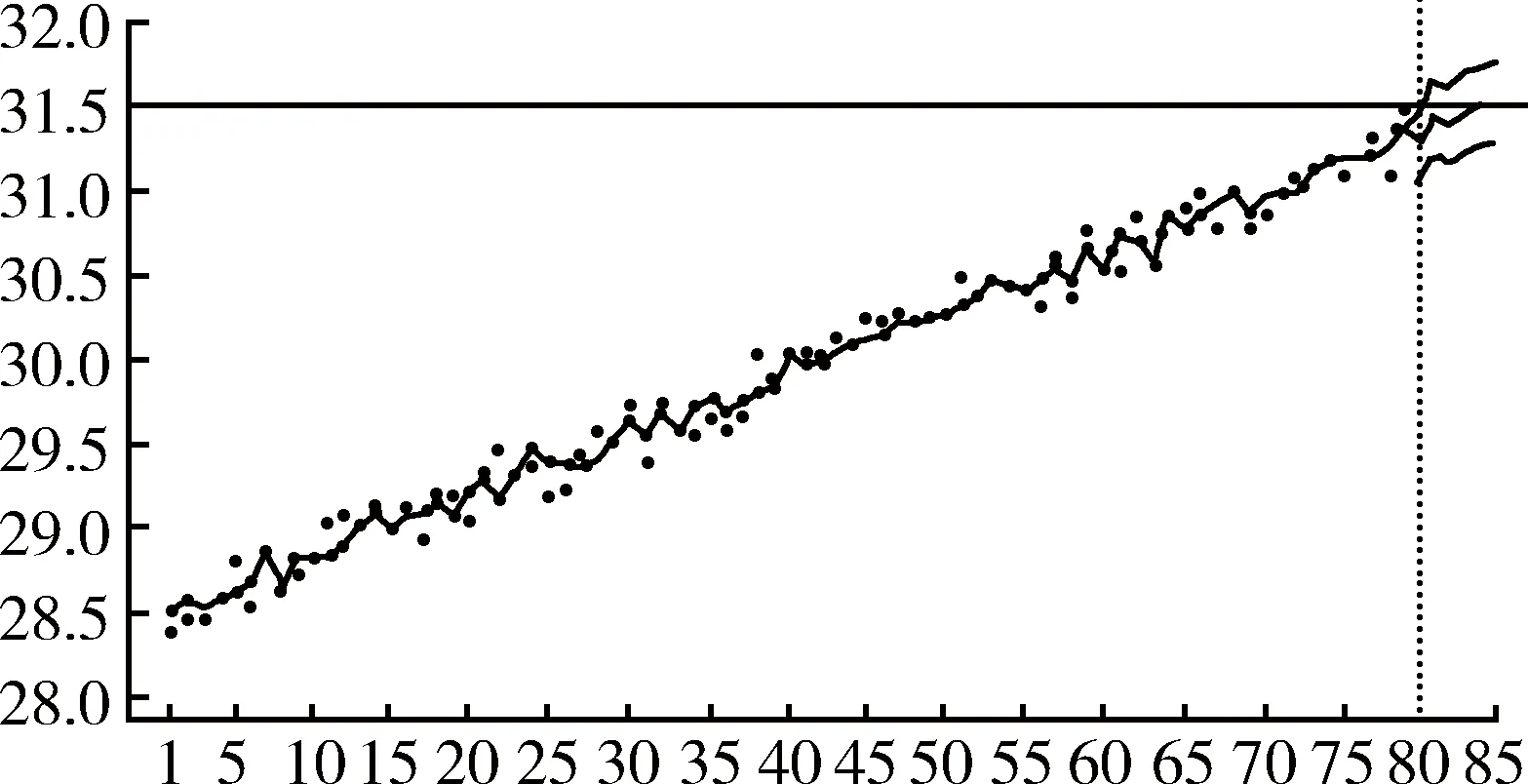
图7 区间预测点线图Fig.7 Dot chart of interzone prediction

由图7中可以看出，幅值为31.5的水平线表示参数的合格上限，用点估计的方法进行预测时，第85个时刻点的估计值超出了合格范围，而实测值正是在第85个时刻点出现了不合格数据，可见点预测的精度较高。在用区间估计的方法进行预测时，第81个时刻点后的预测值上限都超出了参数的合格上限值，说明参数已经具有了超标的可能。在对导弹性能状况进行实际预测研究时，如果某参数指标的预测区间超出或者非常接近合格上下限，则需进行因果分析和故障排查，必要时可更换零部件等，把故障消灭在萌芽状态，避免导致严重后果的发生。

4 结束语

运用成熟的统计分析理论以及数据处理软件，对导弹测试过程中收集到的大量历史数据进行分析处理和数学建模，实现导弹的故障预测，对降低、消除故障危害，提高导弹使用可靠性、安全性等方面都有重要的意义[11]。时间序列趋势预测主要揭示导弹性能指标的变化规律，对未来值的预测通常是给出一个明确的估计值，不能给出精度和范围，预测结果的实用性和可靠性较差，实际运用存在一定的局限性[12]，而统计预测区间技术能够以一定置信度给出数据发展的预测区间范围，解决了时间序列趋势预测技术无精度和范围的缺陷。

参考文献：

[1] 孙振明.预测理论与技术在航天器故障诊断中的应用[D].哈尔滨：哈尔滨工业大学,2004:15-18.

SUN Zhen-ming.The Application of Theory and Technology about Prediction on Fault Diagnosis of Spacecraft[D].Harbin:Harbin Institute of Technology,2004:15-18.

[2] 朱冰静，朱宪辰.预测原理与方法[M].上海：上海交通大学出版社，1991:145-148.

ZHU Bing-jing ,ZHU Xian-chen. Principle and Method of Prediction [M].Shanghai:Shanghai Jiaotong University Press,1991:145-148.

[3] 刘思峰，郭天榜.灰色系统理论及其应用[M].北京:科学出版社，2000:33-136.

LIU Si-feng,GUO Tian-bang.Theory and Application of Grey System[M].Beijing:Science Press,2000:133～136.

[4] 司昕.预测方法中的神经网络模型预测[J]. 预测，1998，17(2):11-13.

SI Xin.the Neural Network Model Prediction based on Prediction Method[J].Forecast，1998，17(2):11-13.

[5] Lapedes,FABER R.Nonlinear Signal Processing Using Neural Network Predicting and System Modeling[R].Los Alams National Laboratory Technical Report,2001:61-64.

[6] 程惠涛.基于神经网络的故障预报技术研究及其在航天器中的应用[D].哈尔滨：哈尔滨工业大学, 1998:23-34.

CHENG Hui-tao. The study of Fault Predication technology based on Neural Network and application on Spacecraft[D].Harbin:Harbin Institute of Technology,1998:23-34.

[7] 李建平，陈廷槐，徐问之,等.从文献分析看小波理论的发展[J] .重庆大学学报:自然科学版,1997，20(6):35-56.

LI Jian-Ping,CHEN Ting-huai,XU Wen-zhi,et al. The Development of Wavelet Theory Based on Literature Analysis[J].Journal of Chongqing University:Natural Science Edition,1997，20(6):35-56.

[8] 张晓东. à Trous小波分解在边缘检测中的应用[J].武汉大学学报:信息科学版,2001，26(1):29-33.

ZHANG Xiao-dong.The Application of Edge Detection Based on à Trous Wavelet Decomposition[J].Journal of Wuhan University:Information Science Edition,2001，26(1):29-33.

[9] 杨叔子，吴雅. 时间序列分析的工程应用[M].武汉：华中理工大学出版社，1992:120-129.

YANG Shu-zi,WU Ya. Engineering Application on Time Series Analysis[M].Wuhan:Huazhong Institute of Technology Press,1992:120-129.

[10] 张有为.预测的数学方法[M].北京：国防工业出版社，1991:156-164.

ZHANG You-wei. Mathematical Method of Prediction[M].Beijing: National Defense Industry Press,1991:156-164.

[11] 杨军.导弹控制系统原理[M].西安:西北工业大学出版社，2000:86-88.

YANG Jun. Principle on Missile Control System[M].Xi′an:Northwestern Polytechnical University Press,2000:86-88.

[12] 孟秀云.导弹制导与控制系统原理[M].北京:北京理工大学出版社，2004:102-114.

MENG Xiu-yun. Principle on Guidance and Control System of Missile[M].Beijing:Beijing Institute of Technology Press,2004:102-114.