基于贝叶斯网络的目标选择方案设计*
贺小亮,毕义明
(1.国防大学 研究生学院,北京 100091;2.第二炮兵工程大学 初级指挥学院,陕西 西安 710025)
0 引言
目标选择[1-2]是指依据联合火力战的作战目的,对战场目标进行分析、计算、对比,从中挑选出最佳打击目标的活动。美军在《目标选择与联合打击条令》中指出,目标选择就是选择目标、排列目标的优先顺序。信息化条件下战场环境更加复杂,可打击的目标类型和数量越来越多,目标之间相互作用构成复杂的目标体系,从而为目标选择带来了严重的挑战。
贝叶斯网络是近几十年来人工智能领域中最重要的研究成果之一,它能够根据不确定或不完整的信息,使用概率论来处理不同知识成分之间的条件相关而产生的不确定性,提供了一种将知识直觉地图解化的方法,是一种新的知识表示模型[3-5]。贝叶斯网络作为一种可描述不确定信息的专家系统,非常适合对目标体系中各类目标之间的不确定关系进行推理决策。根据贝叶斯网络的特点,本文对基于贝叶斯网络的目标选择方法进行了初步探索,叙述了目标选择贝叶斯网络模型的建立和仿真过程。
1 目标选择的概念描述
1.1 目标体系
定义1 不同的单个目标(也可称为子系统、元素和部分)按照某一运行机制相互作用形成一个有机的整体,发挥出某种功能,称之为目标系统[6]。不同的目标系统功能不同,它们之间的相互作用同样形成一个有机的整体,称之为目标体系(target in system of systems, TSS)。
本文在更高层次和更大范围将2个范畴引入目标体系的概念,强调目标体系由多个目标系统组成。为了研究问题方便,根据相似性原理,将目标体系划分为3级层次,目标体系包括目标系统,目标系统又可以由单个目标组成,如图1所示。可以看出,目标体系具有多层次性和多侧面性特点。目标体系各要素在纵向上存在着不同等级的层次关系,其中低一级的要素是高一级要素的基础和有机组成部分。目标体系的某一层上,又可以从横向上把各要素区分为若干互相联系、互相制约、互相作用的部分[7]。
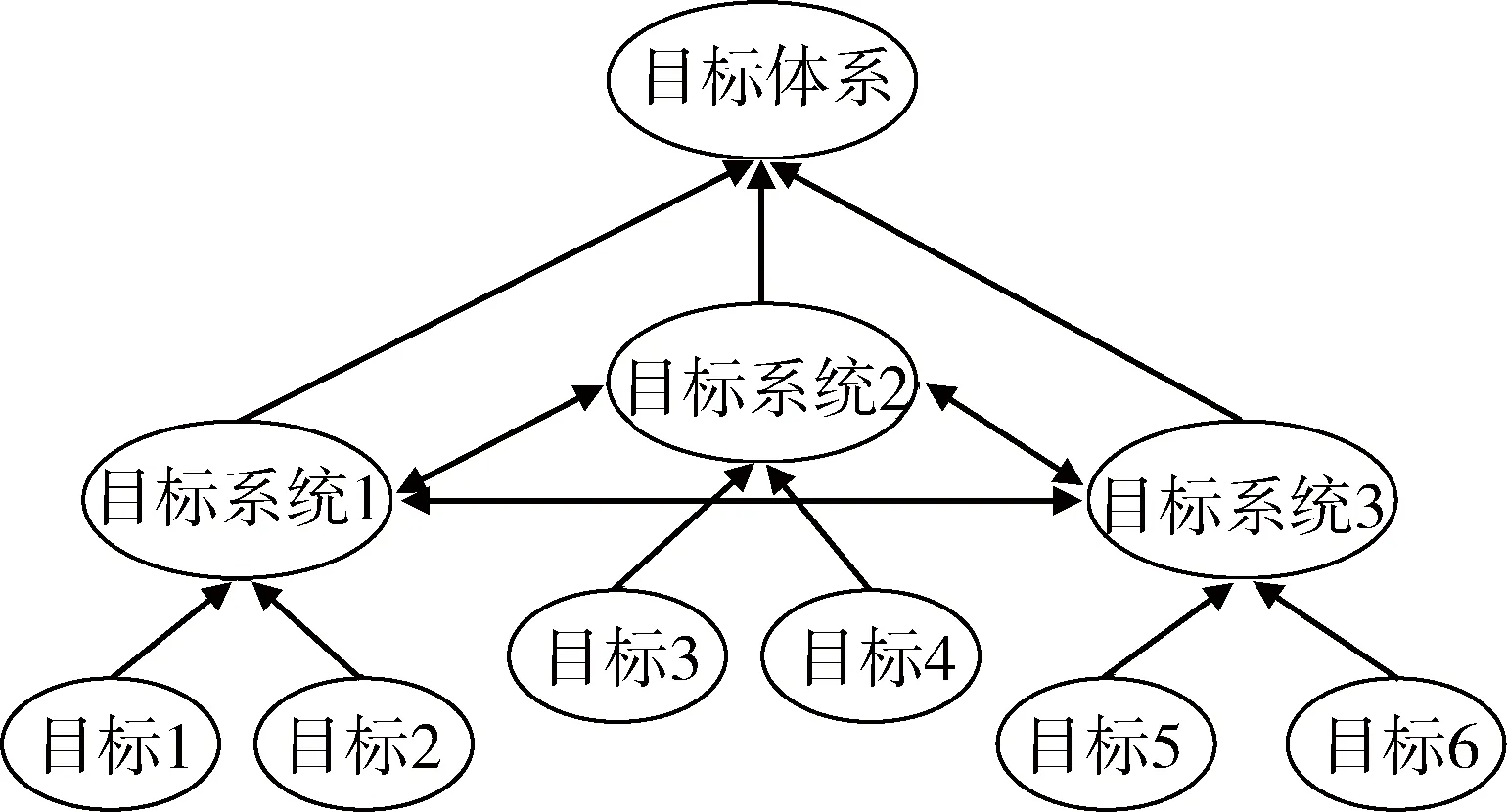
图1 目标体系层次结构Fig.1 TSS architecture
1.2 目标选择
在打击目标体系时,需要考虑体系的支撑点和关键点,打击行动的效果以对体系整体影响效果为衡量,表现为目标体系的崩溃或在体系效能上得到降低[8]。
定义2 目标选择:根据作战目的,运用目标体系分析理论,找出目标体系中起支撑作用的重点目标作为打击对象。
因此,目标选择就是分析和比较目标体系中的各类目标对实现我方战略或战役目的的相对重要程度,找出体系中的关键目标作为重点打击的对象。
2 基于贝叶斯网络的目标选择模型
2.1 贝叶斯网络
贝叶斯网络[8-9]是一种对概率关系的有向图解描述,提供了一种自然的表示事物间因果关系的方法,是综合利用概率论和图论进行不确定事件分析和推理的工具。一个贝叶斯网络由网络结构G和网络参数θ两部分组成。即
B=〈G,θ〉.
网络结构G就是用一个有向无环图(directed acyclic graph, DAG)对变量进行编码,它的节点表示随机变量vi,弧表示变量之间的相互联系,节点变量可以是任何问题的抽象。有向图蕴含了条件独立性假设,贝叶斯网络规定图中的每个节点vi条件独立于由vi的父节点给定的非vi后代节点构成的任何节点子集。假设A(vi)表示非vi的后代节点子集,B(vi)表示vi的直接双亲节点,则
P(viA(vi),B(vi))=P(viB(vi)).
网络参数θ用条件概率表(conditional probability table,CPT)来表示,CPT表达了节点变量与其父节点之间的概率关系,没有任何父节点的节点的条件概率为其先验概率。
有了节点及其相互关系、条件概率表,贝叶斯网络就可以表达网络中所有节点的联合概率,并可以根据先验概率和某些节点的取值计算其他任意节点的概率信息。给定一个随机变量集V=(v1,v2,…,vn),由概率论的链式规则可得变量vi(i=1,2,…,n)的联合概率为
2.2 网络结构的确定
根据目标体系的内部结构及贝叶斯网络的规则,来确定网络结构,形式类似于图1。网络结构能反映出目标体系的内在联系情况。为了方便、高效地得出各类型目标对目标体系效能的相对影响程度,将所有节点的状态设为2种:强(strong,S)、弱(weak,W),分别表示节点目标受到打击后所属能力没有损失和基本完全损失[10]。
2.3 条件概率表的构造
贝叶斯网络结构建立之后,下一个重要的任务就是给定节点的条件概率分布。条件概率的确定需要大量的数据统计和专家知识作为支撑。为了有效地发挥两者的作用,本文采用加权和算法获取节点的条件概率分布。以图2为例,计算节点U的条件概率。
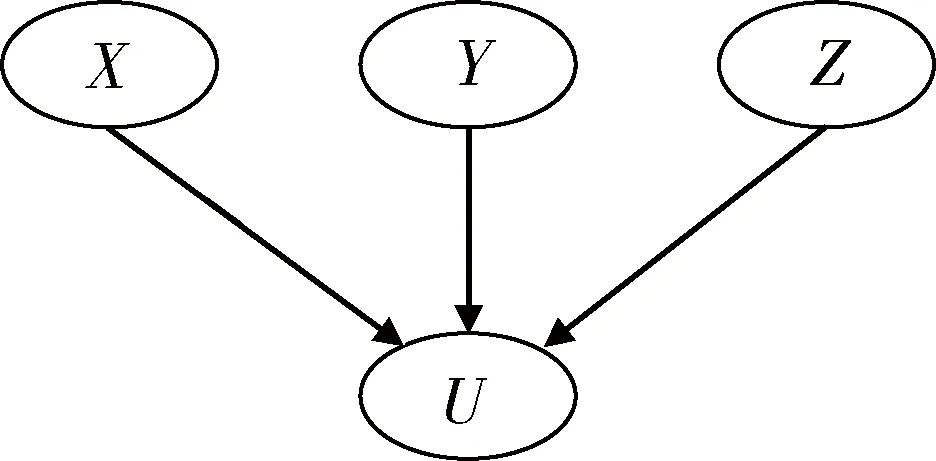
图2 网络结构示例Fig.2 Network structure sample
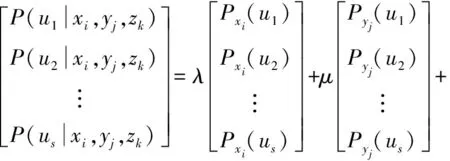
(1)
式中:Pyj(us)为子节点Y在状态yj时,父节点U处于状态us的条件概率,即Pyj(us)=P(usyj)。
式(1)表示节点U的条件概率计算过程,(λ,μ,ν)分别是子节点X,Y,Z对于父节点U的权重系数,并且λ+μ+ν=1,0≤λ,μ,ν≤1。这里,Pyj是通过大量的数据学习得到的,(λ,μ,ν)是专家依据自身经验判断得到的。贝叶斯网络一个卓越的性能就在于其强大的学习能力,无论条件概率还是网络的结构都能够通过数据学习进行更新。在给定每个节点的初始概率之后,就可以通过贝叶斯网络的推理算法获得每个节点所有可能状态的概率分布。
2.4 模型的计算过程
在目标体系的网络结构和条件概率表确定后,需要更新节点的数据,找出关键目标并排列目标的顺序,形成目标选择方案。目标的选择过程分为2个阶段:
第1阶段,将所有的目标状态更新为最强(strongest),根据贝叶斯网络的推理结果,可得到目标体系的最强状态概率。
Pmax=P(TSS=strongestAllTargets=strongest)
第2阶段,将其中目标Ti的状态更新为最弱(weakest),其他目标仍为最强状态,此时,可得到目标体系状态的更新概率。
PTi=P(TSS=strongest|Ti=weakest,
Remain=strongest).
那么,目标Ti相比于其他目标对目标体系的相对影响度(relative impact, RI)为
(2)
随后,依次将其他目标按照第2阶段要求进行数据更新,得到RI。根据计算结果,对所有目标排序,形成目标选择方案。
3 实例仿真应用
以夺取蓝方制空权为例,来验证目标选择贝叶斯网络模型的可行性和有效性。为夺取制空权,即要摧毁蓝方防空力量体系。防空力量体系是由多目标系统及多类型目标构成的,为提高打击效果,节省红方弹药消耗,以摧毁防空力量体系的整体效能为目的,将体系内目标进行排序,找出关键目标,供指挥机构决策。按照1.1节的目标体系划分原则,对防空力量目标体系进行划分。经查阅资料[11-12],防空力量目标体系(air defense TSS, ADTSS)主要是由防空指挥控制系统(air defense command and control system, ADCCS),防空雷达系统(air defense radar system, ADRS),空军基地(air base, AB),地对空导弹系统(ground to air missile system, GAMS),高炮系统(antiaircraft gun system, AGS)等系统组成。防空指挥控制系统主要由指挥机构(command agency, CA),通信枢纽(communication center, CC)等目标组成;防空雷达系统是由管报中心(control and reporting center,CRC),管报站(control and reporting post,CRP),雷达站(radar post,RP)等目标组成;空军基地的主要目标有:跑道(runway),飞机(aircraft),油料(petrol oil lubricant, POL)等。地对空导弹系统包括的主要目标是地对空导弹阵地(ground to air missile position, GAMP)。高炮系统包括的主要目标是高炮阵地(antiaircraft gun position, AGP)。根据防空力量目标体系的组织结构和内部关系,以软件Netcia为仿真平台,构建网络结构,如图3所示。
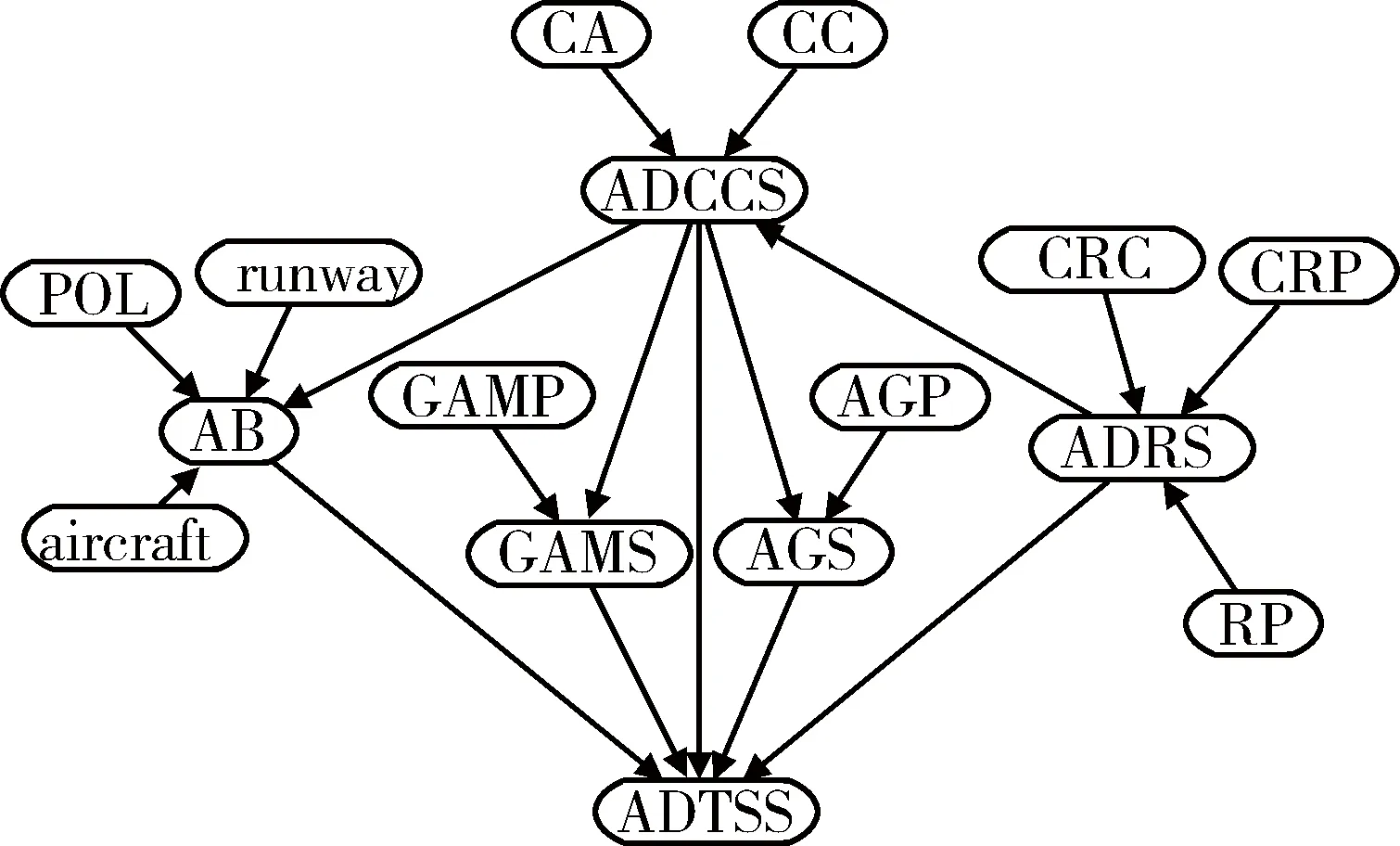
图3 防空力量目标体系网络结构Fig.3 Air defense TSS network structure
根据2.3节节点条件概率获取方法,利用历史数据统计和专家知识,通过参数学习,确定网络中节点的条件概率。以空军基地(air base)为例,其子节点分别是油料(POL),跑道(runway),飞机(aircraft),防空指挥控制系统(ADCCS)。设定子节点对应父节点的权重系数为(λ=0.05,μ=0.5,ν=0.3,β=0.15),空军基地(air base)对应其每个子节点的状态条件概率,如表1所示。
将表1中的数据和子节点的权重系数,按照式
(1)计算得出空军基地对应其子节点的条件概率,如表2所示。
同理,计算得出其他节点目标的条件概率表。将所得条件概率数据,按要求输入以软件Netcia为仿真平台构建的防空力量体系网络结构中,然后按照2.4节模型计算过程的第1阶段要求,将网络中目标节点的状态更新为最强,得到体系更新状态概率Pmax=77.1%,如图4所示。
根据模型计算过程的第2阶段要求,依次将目标节点的状态更新为最弱,得到对应目标体系节点(ADTSS)更新结果PTi(图5是将跑道节点状态更新为最弱时的网络更新结果),再按照式(2),将每个目标对体系的相对影响度计算出来,见表3。其中,指挥机构(CA),管报中心(CRC),地对空导弹阵地(GAMP),跑道(runway)排在前4位,表明这是对防空力量体系效能有重要作用的目标,应进行重点打击。对防空力量体系进行打击时,可按照表3中的结果选择目标,制定打击目标清单。

表1 空军基地对应其每个子节点的条件概率表Table 1 CPT of each child node of air base

表2 空军基地对应其子节点的条件概率表Table 2 CPT of child node of air base

表3 目标相对影响度Table 3 Relative RI of targets
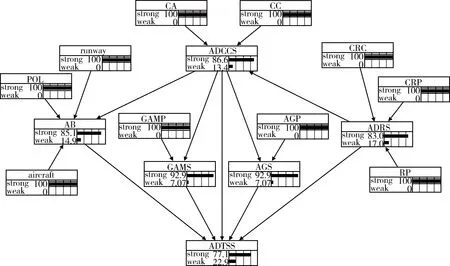
图4 第1阶段网络更新结果Fig.4 First stage of network update result

图5 第2阶段网络更新结果Fig.5 Second stage of network update result
4 结束语
本文针对目标体系构造特点,采用贝叶斯网络,建立了目标选择贝叶斯网络模型,实现了对目标体系内各类型目标初步的重要性分析。以目标对体系的相对影响度为依据,对目标进行排序,找出关键目标,方便指挥机构决策。该方法概念清晰,计算简单,不但能够集成专家的意见和知识,而且还具有强大的数据学习能力和推理能力,充分利用了所有可用信息。通过实例的仿真应用,表明该方法能够按照设计要求,较快地得出结果,验证了模型的有效性和准确性。下一步,将结合各类型目标的特征,对模型进行拓展和研究,实现对目标体系的火力分配和毁伤效果评估。
参考文献:
[1] 胡孝民,应甫成. 联合火力战理论[M]. 北京:国防大学出版社,2003.
HU Xiao-min, YING Fu-cheng. Joint Fire Battle Theory[M]. Beijing: National Defense University Press,2003.
[2] 任富兴,王雪琴. 联合火力战毁伤理论[M]. 北京:解放军出版社,2010.
REN Fu-xing, WANG Xue-qin. Joint Fire Battle Damage Theory[M]. Beijing: PLA Press,2010.
[3] 马志军,贾希胜,陈丽. 基于贝叶斯网络的目标毁伤效果评估研究[J]. 兵工学报,2008,29(12):1509-1513.
MA Zhi-jun, JIA Xi-sheng, CHEN Li. Battle Damage Assessment Based on Bayesian Network[J]. Acta Armamentarii, 2008,29(12):1509-1513.
[4] 雷霆,朱承. 目标体系描述与火力分配方法研究[J]. 军事运筹与系统工程,2012,26(1):67-72.
LEI Ting, ZHU Cheng. Research on the Description and Fire Distribution Method of Target System[J]. Military Operations Research and Systems Engineering, 2012,26(1):67-72.
[5] Pousi Jouni. Decision Analytical Approach to Effects-Based Operations[D].Helsinki: Helsinki University of Technology, 2009:35-63.
[6] 张国春,胡晓峰. 体系对抗仿真中体系效能分析初探[J]. 系统仿真学报,2003,15(12):1698-1701.
ZHANG Guo-chun, HU Xiao-feng. The Initial Study of SoS Effectiveness Analysis in SoS Combat Simulation[J]. Journal of System Simulation, 2003,15(12):1698-1701.
[7] 来淼,王跃利. 面向体系的目标选择形式化描述及分析[J]. 指挥控制与仿真,2007,29(5):26-28.
LAI Miao,WANG Yue-li.Formalized Description and Analysis of Target Selection Model on System of System Oriented[J]. Command Control & Simulation, 2007,29(5):26-28.
[8] 李望西,黄长强,吴文超,等. 空地精确制导武器对地攻击目标毁伤评估[J]. 系统工程理论与实践,2012,32(1):211-218.
LI Wang-xi, HUANG Chang-qiang, WU Wen-chao,et al. Battle Damage Assessment of Air-to-Ground Precision Guided Weapon Air-to-Ground Attack[J]. Systems Engineering Theory & Practice, 2012,32(1):211-218.
[9] David Heckerman. A Tutorial on Learning with Bayesian Networks[R]. Redmond: Microsoft Corporation, 1995.
[10] Lucia Falzon. Using Bayesian Network Analysis to Support Centre of Gravity Analysis in Military Planning[J]. European Journal of Operational Research, 2006,170(9):629-643.
[11] Joint and National Intelligence Support to Military Operations[R]. Joint Staff, 2004.
[12] Joint Intelligence[R]. Joint Staff, 2007.

