自适应旁瓣对消抗灵巧噪声干扰效果研究*
冯明月,何明浩,郁春来,王冰切
(空军预警学院,湖北 武汉 430019)
0 引言
灵巧式噪声干扰这一概念由文献[1]首次提出,文中对于灵巧式干扰与旁瓣对消的关系作出了如下表述:灵巧式噪声干扰不大可能受雷达采用副瓣匿影和旁瓣对消等抗干扰技术的影响。其原因通常解释为灵巧式噪声干扰兼有压制式干扰和欺骗式干扰的特点,而旁瓣对消主要对抗高占空比的类噪声干扰,对于脉冲式的灵巧式噪声干扰,对消性能下降很快,故不大受旁瓣对消的影响。这一概念提出后尽管国内一些学者进行了研究,但都停留在理论阶段,并没有实际的仿真验证[2-4]。
近年来随着高速数字信号处理技术的工程运用不断成熟,开环自适应旁瓣对消技术在新体制相控阵雷达中得到广泛运用[5-6]。采用矩阵求逆法的开环自适应对消技术收敛速度很快,采样数据取5~10即可收敛,因此可以在脉冲干扰期间将权系数收敛为最佳,从而对消脉冲干扰[7]。
基于这样的背景,有必要对于文献[1]中灵巧式噪声干扰不大受旁瓣对消等抗干扰技术影响的描述进行仿真验证,从而深入理解灵巧式噪声干扰的本质,对灵巧式噪声干扰技术进行更加合理的运用,避免干扰资源浪费,同时也可促进自适应旁瓣对消技术的发展。
针对这一问题,本文在理论分析的基础上,通过仿真实验探究了灵巧式噪声干扰样式、调制噪声长度、旁瓣对消快拍时间、干信比等因素对于旁瓣对消抗灵巧式噪声干扰效果的影响,并得出了具有普遍意义的结论。
1 开环旁瓣对消实现
如今新体制相控阵雷达中普遍采用了开环自适应旁瓣对消,旁瓣对消通过设置多个副天线及相应的副通道,来自适应地估计干扰的方向和功率,随后调整雷达主天线接收方向图,将零点置于干扰方向,来抑制通过雷达主天线副瓣进入的具有高占空度和类似噪声的干扰,其原理框如图1所示[8]。
其中,副天线的方向图要和雷达主天线接收方向图的副瓣平均电平近似,且副天线放置在雷达主天线相位中心附近,以保证它们所获得的干扰样本与干扰信号统计相关。为了使主天线接收方向图在N个方向上置零,至少要有N个幅度和相位适当控制的副天线。副天线可以是分列的天线,也可以是相控阵天线的一组接收单元。
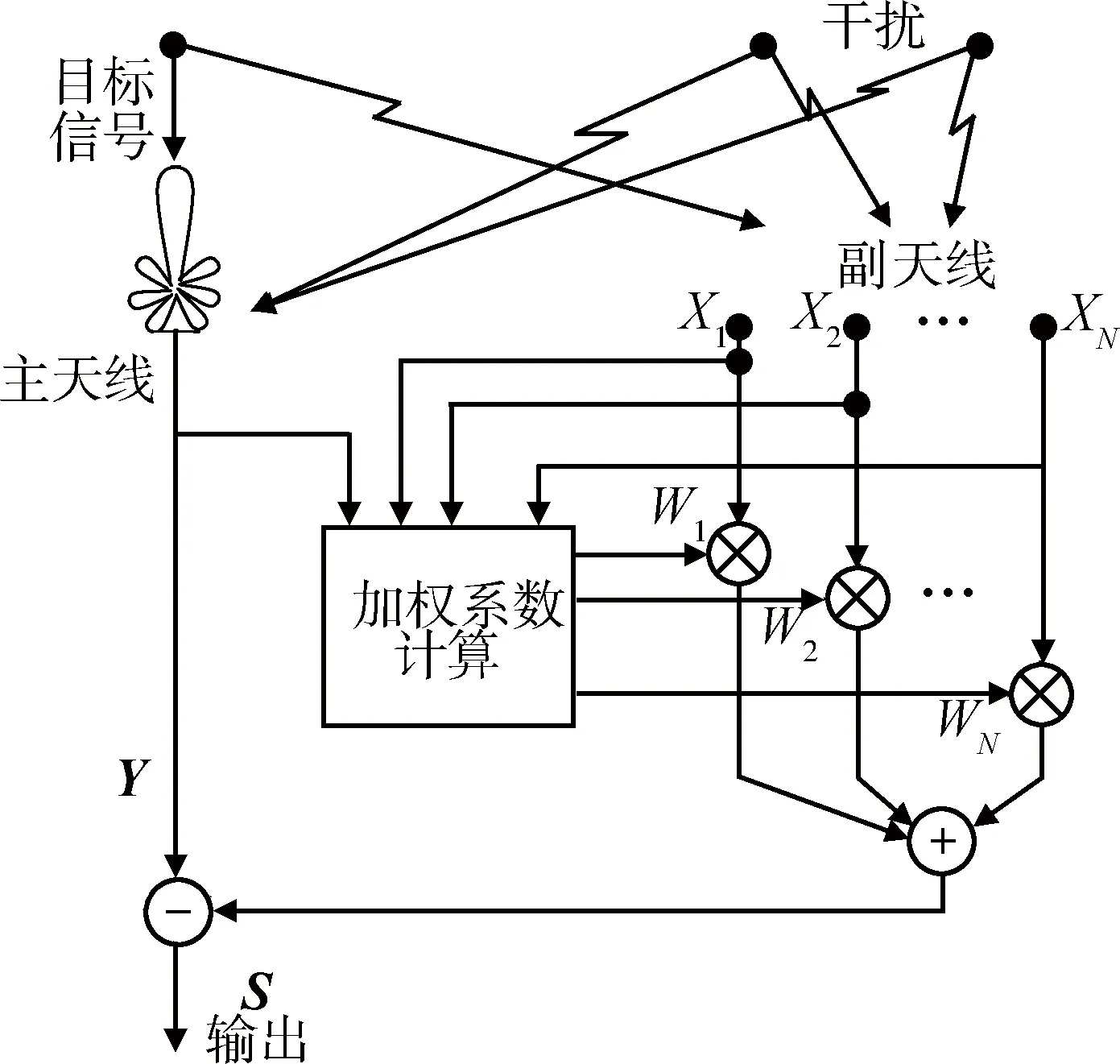
图1 自适应旁瓣对消原理Fig.1 Theory of adaptive sidelobe canceling
图中,用Y表示主天线接收信号,用N维矢量X=(X1,X2,…,XN)表示N个副天线的接收信号,用N维矢量W=(W1,W2,…,WN)表示旁瓣对消权系数,用S表示旁瓣对消输出结果。因此,图1的数学模型为
S=Y-WHX,
(1)
式中:上标H表示共轭转置。
旁瓣对消的目的是使对消结果S最小,按照最小均方准则(least mean square,LMS),在输出S的均方值最小的条件下,最优权值Wopt可通过维纳—霍夫方程进行求解。
Wopt=R-1d,
(2)
式中:R=E(XXH)为副天线输入的自相关矩阵;d=E(XY*)为主天线和副天线输入信号的互相关矩阵。
对于维纳—霍夫方程的推导过程可以参考文献[5],本文不进行详细叙述。利用式(2)直接进行最优权值的计算,即为实现开环旁瓣对消的矩阵求逆算法。
2 灵巧噪声对消分析
2.1 灵巧噪声干扰产生原理
利用卷积调制产生灵巧式噪声干扰是目前较为普遍的一种方法[9-11],其特点是不需要测频就能干扰频率捷变的脉冲压缩雷达,还可利用脉冲压缩的处理增益,降低干扰功率要求。基本原理如下:
假设雷达发射信号为线性调频信号s(t),目标的回应函数为
h(t)=σδ(t-tR),
(3)
式中:σ为目标的反射截面积;tR为目标回波时延。
则目标回波为
sr(t)=s(t)⊗h(t).
(4)
雷达脉冲压缩处理响应函数为s*(-t),匹配滤波后表达式为
spc(t)=s*(-t)⊗s(t)⊗h(t)=
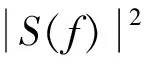
(5)
从式(5)中可以看出,任意函数同线性调频信号相卷积,其脉冲压缩输出信号为该函数与点扩展函数的卷积,也就是说获得了雷达的脉冲压缩处理增益,如果将目标响应函数h(t)变为干扰调制信号,则干扰信号也可以获得雷达的脉冲压缩处理增益。
2.2 通道噪声对对消结果影响
开环旁瓣对消输入的干扰信号中不仅包含了灵巧噪声干扰信号,还包含了不可避免的通道噪声信号。在利用基于最小均方误差准则计算最优权值的过程中,通道噪声信号也包含在了辅助通道和主通道的输出信号当中,其时长等于旁瓣对消的快拍时间,并且在某些条件下,通道噪声信号也会对灵巧噪声干扰的对消效果产生影响。
为了更好地描述通道噪声信号对于旁瓣对消最优权值计算的影响,引入影响因子的概念。定义为某一信号对于旁瓣对消最优权系数计算的影响程度,用符号ε表示,所有参与对消运算的信号对应的影响因子有如下关系:
(6)
从式(6)中可以归纳出影响因子的3个性质:
(1)n个参与旁瓣对消的信号的影响因子之和为1,即在旁瓣对消过程中,最优权系数的计算只由旁瓣对消快拍时间内的采样信号所确定,而与其他因素无关。
(2) 每一个信号的影响因子都大于0小于等于1,即只要快拍时间内存在某一种信号的采样,该信号就会对旁瓣对消最优权值的计算产生影响。
(3) 不同信号的影响因子之间相互关联,根据旁瓣对消原理,某种信号的影响因子与其在快拍时刻内的采样点数和信号功率有关,功率越大采样点数越多影响因子也就越大,反之亦然。
设开环旁瓣对消的快拍时间为TR,快拍时间内总的干扰信号为
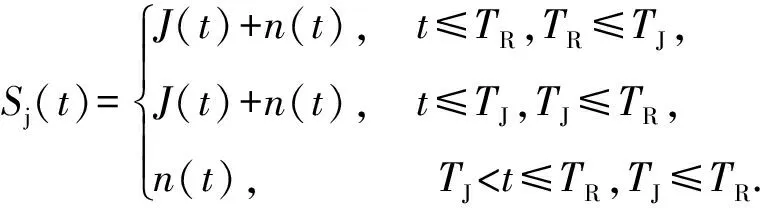
(7)
当旁瓣对消的快拍时间TR小于干扰持续时间TJ时,相当于对干扰信号从TR时刻进行截断,此时快拍的采样样本中都包含了灵巧噪声干扰信号和通道噪声信号,在相同采样点数的情况下,由于干扰信号功率大于通道噪声功率,所以噪声信号n(t)的影响因子小于干扰信号J(t),并且二者之间功率相差越大,噪声信号的影响因子越小。因此,在较大的干扰噪声功率比下,旁瓣对消结果将主要由灵巧噪声信号所决定,此时对于灵巧噪声信号将具有较好的对消性能。
当旁瓣对消的快拍时间TR大于干扰持续时间TJ时,快拍输入干扰信号Sj(t)中包含了TJ采样时长的干扰信号和TR采样时长的噪声信号。设快拍点数为M,噪声点数为N,则这种情况下式(7)化简为
(8)
由式(8)可知,在计算最优权值的过程中,在前N个采样点,噪声和干扰具有相同的采样时长,由于干扰功率大于噪声功率,干扰信号的影响因子要大于噪声信号。但在后M-N个点中,由于不包含干扰信号,此时噪声将具有很大的影响因子。将前后2种情况进行综合,可得如下结论:①固定干扰噪声功率比,若M/N较小,前N点的影响因子对最终影响因子影响较大,则噪声信号最终的影响因子较小,对旁瓣对消结果影响较小,此时旁瓣对消对于灵巧噪声信号仍具有较好对消效果;若M/N较大,则不能忽略后M-N点的影响因子对于最终影响因子的影响,此时噪声信号可能会影响最终的对消结果,具体结论还需进一步讨论干扰噪声功率比,来确定噪声信号的最终影响因子。②固定M/N,干扰噪声功率比越大,噪声信号的影响因子越小,其对于旁瓣对消最终结果的影响也就越小。
3 仿真分析
3.1 分析指标
通常利用干扰对消比(jamming cancelling rate,JCR)即在没有目标信号的条件下,无辅助天线时干扰输出功率与有辅助天线时干扰的输出功率之比来衡量旁瓣对消性能[12-13]。
(9)
干扰对消比是一个相对量,能够体现自适应旁瓣对消处理对于干扰信号的抑制情况。除此之外,旁瓣对消后的合成方向图可以更加直观地表现出雷达对于特定方向干扰的抑制情况,并且零点深度和方向图形状可用于不同干扰对消效果间的横向比较[2]。因此,本文利用干扰对消比和合成方向图2个指标来描述自适应旁瓣对消对于灵巧式噪声干扰的作用效果。
3.2 实验分析
雷达主天线采用线阵天线,主天线阵元为30个,阵元间距与发射信号波长之比为0.5,图2给出了主天线方向图。有一个独立的全向辅助天线,辅助天线位于中心阵元的上方,辅助天线增益略大于主天线第1旁瓣增益。雷达发射信号为线性调频信号,信号带宽B=10 MHz,脉宽τ=10 μs,重复频率PRF=5 kHz,目标回波入射角与线阵法线夹角θ=0°,采样频率Fs=40 MHz,雷达回波信噪比SNR=10 dB。
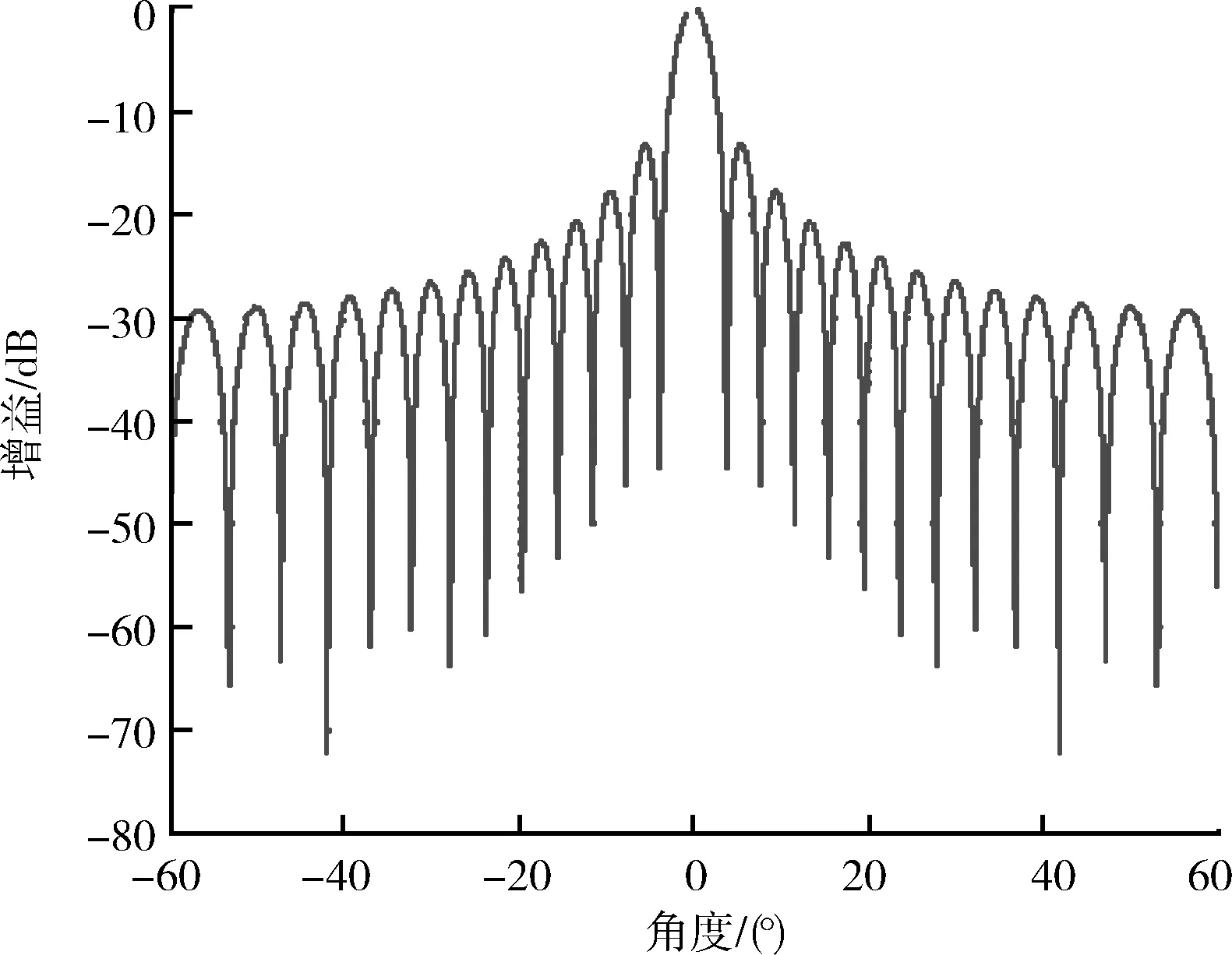
图2 主天线方向图Fig.2 Directional diagram of main antenna
3.2.1 灵巧噪声干扰对消方向图
为了验证旁瓣对消后合成方向图的变化情况,进行如下实验:实验1进行灵巧噪声干扰,调制噪声长度TJ=20 μs,自适应旁瓣对消的快拍时间TR=50 μs,干信比为20 dB,干扰入射角与法线夹角θ=5°;实验2进行射频噪声干扰,干扰持续时间TJ=200 ms,其他条件与灵巧噪声干扰相同。图3给出了2个实验的合成方向图。

图3 合成方向图对比Fig.3 Comparison of combined directional diagram
通过对比发现,自适应旁瓣对消均可在2个干扰的到达方向形成低副瓣,证明了自适应对消处理的有效性。而2种干扰样式区别在于射频噪声干扰在干扰方向上的凹陷更深,抑制效果更好。灵巧噪声干扰对消后的合成方向图较射频噪声干扰的合成方向图主瓣没有明显展宽,第1副瓣电平没有抬高,整体形状基本类似,没有造成合成方向图畸变。通过对比实验可证明,自适应旁瓣对消和干扰波形无关,灵巧式噪声干扰同样可以在干扰方向上形成凹陷,具有一定的对消效果。
3.2.2 调制噪声长度与快拍时间关系
为了探究灵巧式噪声干扰调制噪声长度与旁瓣对消快拍时间的关系,进行如下实验:快拍时间TR分别取30,60,90,120 μs,调制噪声长度TJ范围0.1 ~120 μs、步长0.5 μs,干信比为20 dB,干扰入射角与法线夹角θ=5°,同一快拍时间下每个调制噪声长度进行100次蒙特卡罗实验,计算100次蒙特卡罗实验的平均干扰对消比作为最后的干扰对消比。实验结果如图4所示。
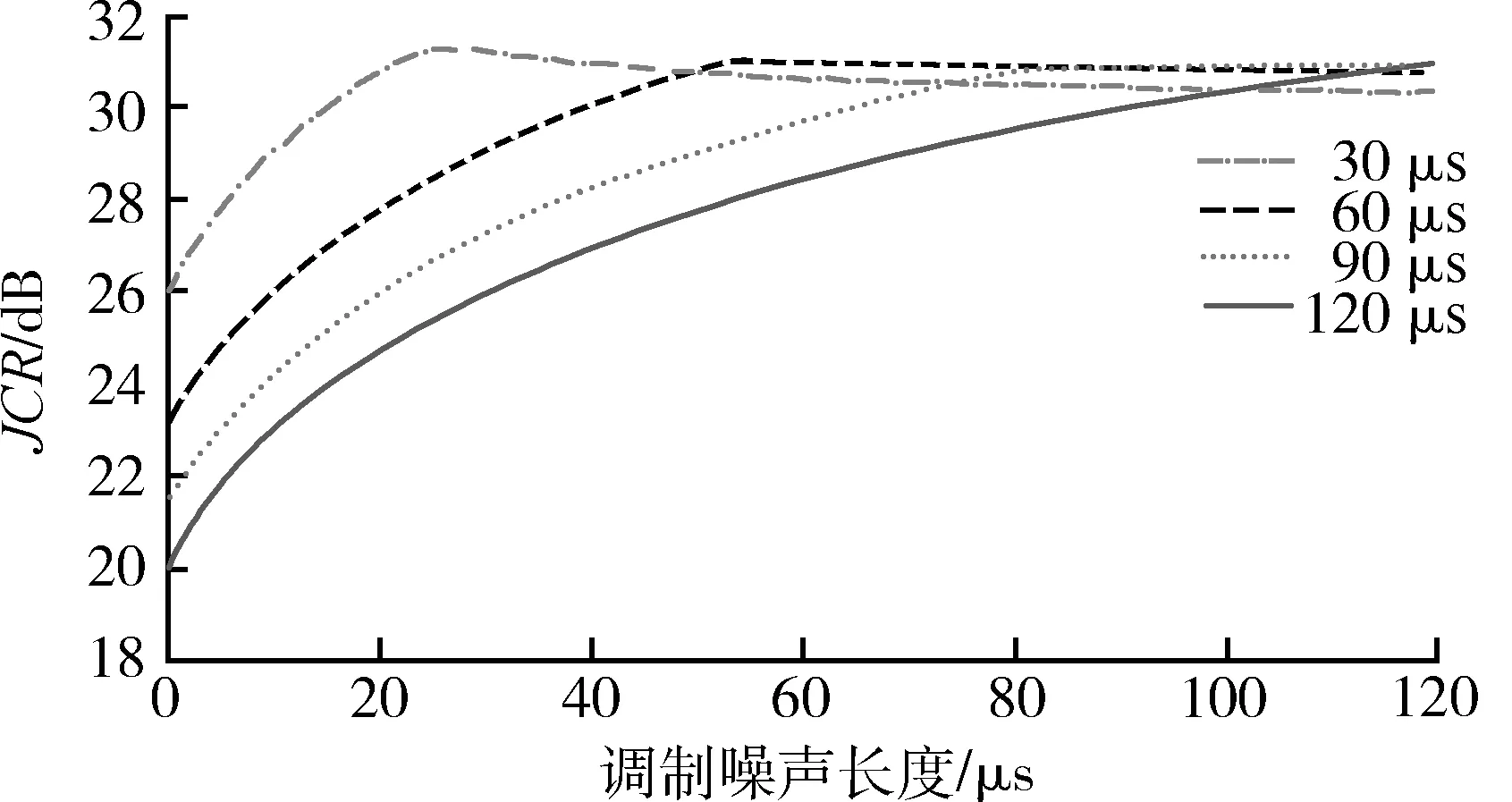
图4 调制噪声长度对消效果图Fig.4 Canceling effect about the length of modulating noise
通过图4可得以下2点结论:①同一快拍时间下,干扰对消比随着调制噪声长度增大而变大,当调制噪声长度大于快拍时间时,干扰对消比为最大,随后基本保持不变。②同一调制噪声长度下,快拍时间越短,干扰对消比越大,对消效果越好。因此,对于雷达而言,适当降低自适应旁瓣对消的快拍时间可以增大对于灵巧式噪声干扰的抑制效果。
3.2.3 干信比与调制噪声长度关系
为了探究干信比同调制噪声长度的关系,进行如下实验:快拍时间TR=90 μs,调制噪声长度TJ分别取30,60,90 μs,干信比JSR范围0~30 dB、步长0.1 dB,干扰入射角与法线夹角θ=5°,同一快拍时间下每个调制噪声长度进行100次蒙特卡罗实验,计算100次蒙特卡罗实验的平均干扰对消比作为最后的干扰对消比。实验结果如图5所示。
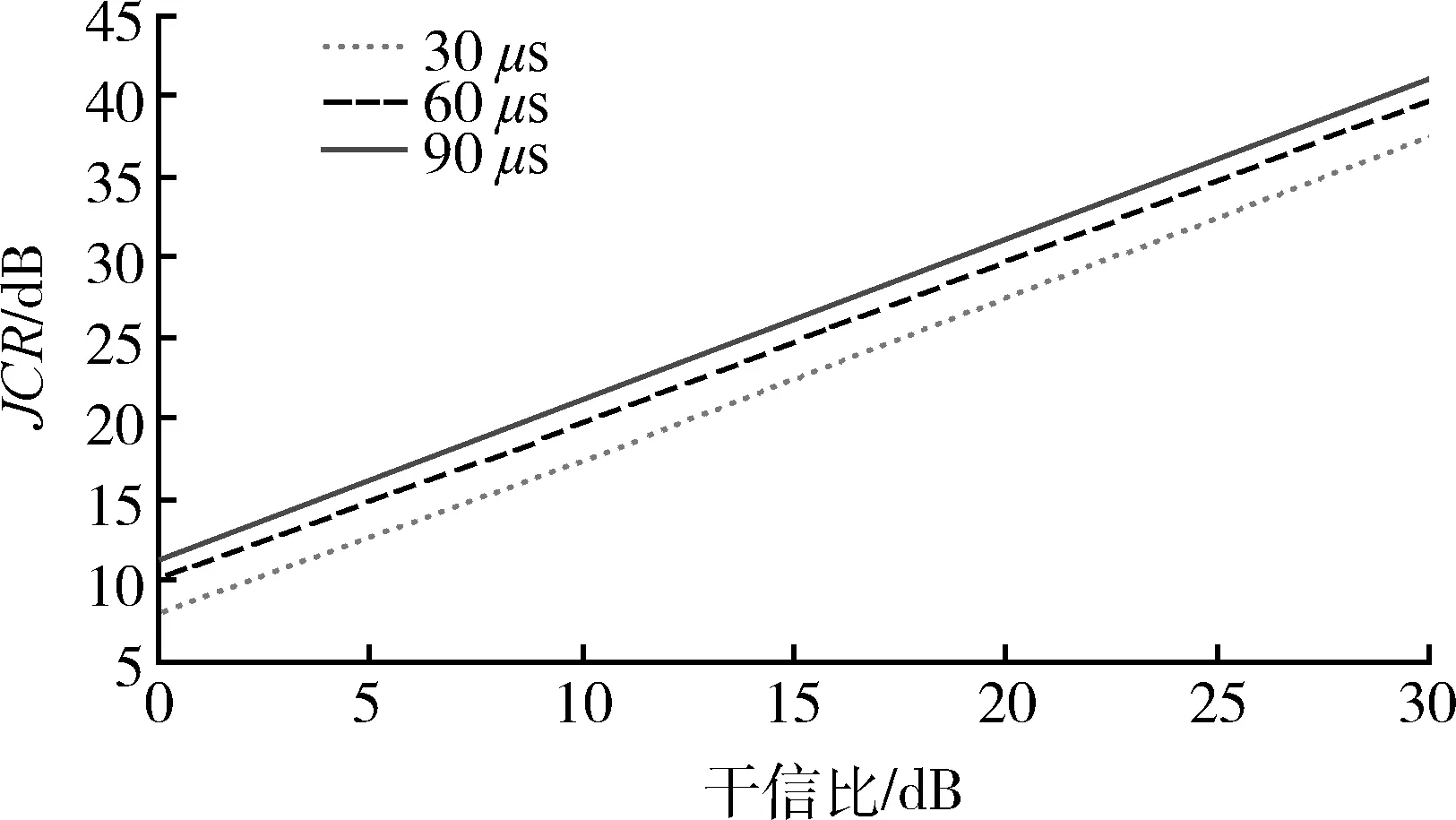
图5 干信比对消效果图Fig.5 Canceling effect about JCR
通过图5可以得到以下3点结论:①在同一调制噪声下,干扰对消比随着干信比增加逐渐增大,干信比越大,旁瓣对消的抑制效果越好。②同一干信比下,不同调制噪声长度的干扰对消比相差不大,约为2~3 dB,并且这一差距基本不随干信比增加而变化。③从图中可以看出,3条线的斜率基本相同,故干信比对于对消效果的影响程度与调制噪声长度无关。
4 结束语
通过2.2节中利用影响因子从理论角度的定性分析和3.2节中利用仿真实验的定量分析,可以发现,2种分析方法的结论是一致的,接收通道噪声的存在确实会影响开环旁瓣对消对于灵巧噪声干扰的对消效果,具体而言,主要有以下4点关系:
(1) 自适应旁瓣对消技术可以抑制灵巧式噪声干扰,且不会造成合成方向图畸变,这一性质和旁瓣对消干扰波形无关。
(2) 减小自适应旁瓣对消的快拍数可以提高对于灵巧式噪声干扰的抑制效果,更加有效地抑制灵巧噪声干扰。
(3) 灵巧式噪声干扰的调制噪声长度越长,越容易受到旁瓣对消技术的抑制,应在保证压制性效果的基础上尽可能降低调制噪声长度。
(4) 灵巧式噪声干扰的干信比越大,受旁瓣对消抑制越明显,干信比的影响程度在不同调制噪声长度下基本相同,与调制噪声长度无关。
以上结论可为今后灵巧式噪声干扰和旁瓣对消技术的理论研究和实际运用提供参考,具有重要的理论和实践意义。
参考文献:
[1] SCHLEHER D C. Electronic Warfare in the Information Age[M]. Norwood MA: Artech House, 1999.
[2] 栾琳. 灵巧噪声干扰的建模仿真研究[D].西安:西安电子科技大学, 2009.
LUAN Lin. Modeling Simulation and Study of Smart Noise Jamming[D].Xi′an:Xidian University, 2009.
[3] 邱杰. 灵巧噪声干扰与旁瓣消隐技术关系探讨[J]. 现代雷达,2012, 34(8): 55-59.
QIU Jie. A Study on Relationship Between Smart Noise Jamming and SLB[J]. Modern Radar,2012, 34(8): 55-59.
[4] 邱杰,邱丽原. 灵巧噪声干扰本质及相关基本问题探讨[J]. 现代防御技术,2012, 40(3): 132-136.
QIU Jie, QIU Li-yuan. Essential Signification of Smart Noise Jamming[J]. Modern Defence Technology,2012, 40(3): 132-136.
[5] 林仁春. 雷达干扰旁瓣对消器实现方法研究[D].成都:电子科技大学, 2011.
LIN Ren-chun. Realization of Radar Sidelobe Canceler [D].Chengdu: University of Science and Technology of China, 2011.
[6] 宁勇. 对相控阵雷达旁瓣干扰方法研究[J]. 电子对抗,2009(6):1-7.
NING Yong. Sidelobe Jamming Against the Phased-Array Radar[J]. Electronic Warfare, 2009(6):1-7.
[7] 白渭雄,张文,苗淼. 旁瓣干扰对抗技术研究[J]. 系统工程与电子技术,2009,31(1): 86-90.
BAI Wei-xiong, ZHANG Wen, MIAO Miao. Study on the Countermeasure Technology Against Side-Lobe Interference[J]. Systems Engineering and Electronics, 2009,31(1): 86-90.
[8] 刘卫平. 相控阵雷达基于部分阵元的旁瓣对消系统设计[D].西安:西安电子科技大学, 2009.
LIU Wei-ping. Design of Phased Array Radar SLC System by Selecting Partial Antennas[D].Xi′an: Xidian University, 2009.
[9] 张煜,杨绍全. 对线性调频雷达的卷积干扰技术[J]. 电子与信息学报,2007, 29(6): 1408-1411.
ZHANG Yu, YANG Shao-quan. Convolution Jamming Technique Conntering LFM Radar[J]. Journal of Electronics & Information Technology,2007, 29(6):1408-1411.
[10] 葛青林,王莹莹,李静. 一种产生雷达多假目标的卷积调制法[J]. 现代防御技术, 2012, 40(1): 137-139.
GE Qing-lin, WANG Ying-ying, LI Jing. A Kind of Convolution Modulation Method that Generate Radar Multi-False Target[J]. Modern Defence Technology, 2012, 40(1): 137-139.
[11] 顾海燕,卢刚,唐斌. 一种卷积干扰特征分析与识别方法[J]. 现代雷达, 2011, 33(3):39-43.
GU Hai-yan, LU Gang, TANG Bin. A Method of Characteristic Analysis and Identification on Convolution Jamming[J]. Modern Radar,2011, 33(3):39-43.
[12] 刘潮,李政杰,童宁宁. 自适应旁瓣对消分析与仿真[J]. 现代防御技术, 2011, 39(2): 148-152.
LIU Chao, LI Zheng-jie, TONG Ning-ning. Analysis of Adaptive Sidelobe Canceller and Its Simulation[J]. Modern Defence Technology,2011, 39(2): 148-152.
[13] 李森,李彦志,张国毅,等. 对自适应旁瓣对消系统的闪烁干扰方案研究[J]. 现代雷达,2012, 34(2): 51-54.
LI Sen, LI Yan-zhi, ZHANG Guo-yi,et al. A Study on Twinkle Jamming Project Against the Adaptive Sidelobe Canceling System[J]. Modern Radar,2012, 34(2):51-54.

