车载捷联惯导/重力匹配/高度计组合导航方法*

杨波，王跃钢，孟朝，郭志斌

(1.第二炮兵工程大学 自动控制系，陕西 西安 710025； 2.中国人民解放军96819部队，北京 100015)

0 引言

现代战争中，为了增强发射车、指挥车、装甲车等特殊军用车辆的快速机动性，要求其具备精确的实时导航定位能力，特别要求在战场恶劣环境下具备较强的独立自主性和抗干扰性。目前，国内外广泛研究采用了以卫星/航位推算或惯导/卫星组合导航为主要模式的车载导航定位技术[1-3]。但是，由于卫星导航信号容易被遮挡或干扰，在战场环境下不能绝对依赖，而一旦卫星导航失效，仅靠航位推算或惯导本身无法实现较高精度导航定位，因此上述2种模式的独立自主性和抗干扰能力较差。

由于重力场信息具有抗干扰能力强、全天候、无源性等优点，因此基于重力场的重力匹配导航系统是一种完全自主式导航系统，它既不向外发射信号，也不从外部接收信号，自主性和抗干扰能力非常强，成为近几年来导航领域研究的前沿和热点[4-5]。重力匹配导航通常利用重力传感器(如重力仪)实时测量的重力异常值与事先储存的数字重力异常图进行匹配，从而获得载体的水平位置信息[6]。由于惯导系统也是一种抗干扰性强的完全自主式导航系统，但存在误差随时间不断发散的缺陷，如果利用重力导航系统辅助惯导系统进行误差修正，构成组合导航系统，则可以实现完全自主性、强抗干扰性和高隐蔽性[7]，特别是能够有效应对战场恶劣环境下各种电磁干扰，这在军事应用领域具有重要价值。

为此，本文将捷联惯导、重力匹配和气压高度计组合起来进行车载导航定位，其中引入气压高度计是为了弥补重力匹配导航无法获得高度信息的缺陷。首先，建立了重力匹配导航的误差模型，将捷联惯导与重力匹配导航的误差作为系统状态，建立对应的系统状态方程；然后，将重力匹配获得的水平位置、高度计输出的高度与捷联惯导输出的对应信息相减作为量测，建立量测方程；接着，采用对系统模型具有较好鲁棒性的Sage-Husa自适应滤波进行组合导航滤波设计，并针对重力匹配导航非等间隔输出问题，对滤波方程进行了改进，从而获得捷联惯导/重力匹配/高度计组合导航滤波算法。

1 捷联惯导/重力匹配/高度计组合导航方案

采用东-北-天地理坐标系作为导航坐标系。捷联惯导、重力匹配导航系统与气压高度计均捷联安装在载车上。捷联惯导经过导航解算输出载车的姿态、位置和速度信息，重力匹配导航系统输出载车水平位置信息，气压高度计输出高度信息。

在捷联惯导/重力匹配/高度计组合导航系统中，首先将捷联惯导输出的载体水平位置与重力匹配导航输出的对应信息相减作为量测Z1，将捷联惯导输出的载体高度与气压高度计输出的高度相减作为量测Z2，获得组合导航的量测；接着，将2部分量测Z1，Z2同时送入组合导航滤波器(本文采用自适应滤波)进行滤波计算，从而获得系统状态(包含捷联惯导系统误差)的估计值；最后，利用所获得的捷联惯导系统误差估计值实时对捷联惯导进行误差校正，并将校正后的捷联惯导系统输出作为捷联惯导/重力匹配/高度计组合导航系统的输出。因此，该组合导航方案如图1所示。

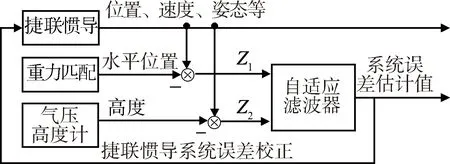
图1 捷联惯导/重力匹配/高度计组合导航方案框图Fig.1 Schematic diagram of SINS/gravity matching/altimeter integrated navigation

2 捷联惯导/重力匹配/高度计组合导航系统状态方程

本文采用间接法滤波，即选取系统误差作为捷联惯导/重力匹配/高度计组合导航滤波器的状态，为此需要对捷联惯导、重力匹配导航系统和气压高度计分别进行误差分析与建模。捷联惯导的误差方程在很多文献中已有研究，在此不作赘述，本文重点分析重力匹配导航的误差和气压高度计的误差。

2.1 重力匹配导航系统的误差模型

重力匹配导航的误差通常由重力传感器测量误差、数字重力图制作误差、厄特弗斯效应估计误差以及重力匹配算法误差等因素所引起[8]。由于影响因素复杂，在组合导航设计中不宜对重力匹配导航的各种误差逐一进行建模，但可以采用Box-Jenkins时间序列分析技术，对重力匹配导航实测数据的随机误差进行模型辨识。通过辨识发现，重力匹配导航的随机误差是一个非平稳的随机过程，因此其可以表示为一个随机游走和白噪声的组合，即重力匹配导航系统的误差模型为

δLG=NL+wL，

(1)

(2)

δλG=Nλ+wλ，

(3)

(4)

式中：δLG,δλG分别为重力匹配导航的纬、经度误差；NL,Nλ为随机游走；wL,wNL,wλ,wNλ为零均值的白噪声。

2.2 气压高度计的误差模型

气压高度计通过测量环境大气静压力来间接测量载体高度，其测量精度易受大气环境(大气压力和温度)的影响，且测量误差随高度增加而增加[9-10]。由于大气环境变化一般比较缓慢，因此短时间内气压高度计精度较高；而且，对于低空环境而言，尤其是地面车载运动环境，气压高度计具有很高的精度，甚至优于GPS的高度精度，达到数十米精度[11]。因此，本文在组合导航设计中为了降低滤波器的维数，将气压高度计的误差直接考虑为白噪声，而不需再对其进行误差建模，也不再列入组合导航系统状态。

2.3 组合导航系统的状态方程

由于采用间接法滤波，因此选取各导航设备的误差作为捷联惯导/重力匹配/高度计组合导航滤波器的状态X，即包括捷联惯导的数学平台姿态误差角φE,φN,φU，速度误差δvE,δvN,δvU，位置误差δL,δλ,δh，陀螺常值漂移εbx,εby,εbz，加速度计常值误差▽bx,▽by,▽bz；重力匹配导航的水平位置误差δLG,δλG，则

X=(φE,φN,φU,δvE,δvN,δvU,δL,δλ,δh,εbx,

εby,εbz,▽bx,▽by,▽bz,δLG,δλG)T.

(5)

于是，根据捷联惯导、重力匹配导航系统和气压高度计的误差模型，并结合系统状态X，可列写出捷联惯导/重力匹配/高度计组合导航系统的状态方程为

(6)

式中：F为系统状态矩阵；G为系统噪声驱动阵；W为系统白噪声。

W=(wgx,wgy,wgz,wax,way,waz,wNL,wNλ)T，

式中：wgx,wgy,wgz为陀螺白噪声；wax,way,waz为加速度计白噪声。

3 捷联惯导/重力匹配/高度计组合导航量测方程

将捷联惯导输出的载体水平位置与重力匹配导航输出的对应信息相减作为捷联惯导/重力匹配/高度计组合导航的量测之一Z1，即

Z1=(LS-LG,λS-λG)T，

(7)

式中：LS,λS分别为捷联惯导输出的纬、经度；LG,λG分别为重力匹配导航系统输出的纬、经度。

由于重力匹配导航系统仅能输出载体水平位置信息，这样就无法对捷联惯导的高度误差进行有效修正，为此需要引入气压高度计，借助其高精度的高度信息来修正捷联惯导的高度误差。因此，将捷联惯导输出的载体高度与气压高度计输出的高度相减作为捷联惯导/重力匹配/高度计组合导航的另一部分量测Z2，即

Z2=(hS-hA)，

(8)

式中：hS,hA分别为捷联惯导、气压高度计输出的载体高度矢量。

于是，根据式(7)和(8)，并结合组合导航系统状态X，可列写出捷联惯导/重力匹配/高度计组合导航系统的量测方程为

Z=HX+V，

(9)

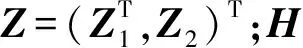
4 基于自适应滤波的组合导航滤波算法

目前，组合导航设计中广泛采用了标准卡尔曼滤波，其对系统模型比较敏感。由于本文所建立的重力匹配导航系统误差模型与匹配率有很大关系，如果匹配率大幅降低，将使该重力匹配导航系统误差模型与真实系统存在较大差距。而一旦所建立的系统模型失真，不仅会使卡尔曼滤波精度下降，甚至可能导致滤波发散[12]。因此，为了提高捷联惯导/重力匹配/高度计组合导航滤波器的稳定性，本文采用了对系统模型具有较好鲁棒性的Sage-Husa自适应滤波进行组合导航滤波设计。

需要注意的是，由于重力匹配导航过程中存在着匹配失败的可能性，因此在工程实际中重力匹配导航是非等间隔地输出导航参数，而且每次输出间隔的时间也相对较长，这将给滤波器设计带来困难，而且明显降低滤波精度。为此，本文对Sage-Husa自适应滤波方程进行了改进，从而获得适用于捷联惯导/重力匹配/高度计组合导航的滤波算法。

设捷联惯导解算周期为TSINS，重力匹配导航输出的时间间隔为TGNSi(i=1,2,3，…)，滤波周期为T。令T=NTSINS，TGNSi=MiT，这里Mi，N均为正整数，其中N固定不变，而Mi不断变化。当滤波周期T到来而重力匹配导航信息还没到来时，此时采用式(10)～(11)进行滤波。

(10)

(11)

而当重力匹配导航信息到来时，则采用式(12)～(18)进行滤波。

(12)

(13)

(14)

(15)

(16)

(17)

Pk=(I-KkHk)Pk/k-1,

(18)

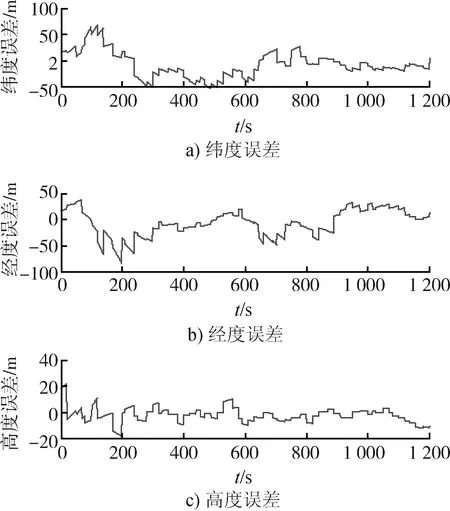
式中：dk=(1-b)/(1-bk+1)，0

b的选取可按实际情况而定：当估计参数变化较快时，b取值偏小；反之，当估计参数变化较慢时，b取值则偏大。

从而，利用式(10)～(18)就可以有效解决重力匹配导航非等间隔输出和输出周期较长时的组合导航滤波问题。经过滤波计算获得捷联惯导系统误差的估计值以后，需要对捷联惯导及时进行误差校正，并将误差校正后捷联惯导的输出作为捷联惯导/重力匹配/高度计组合导航系统的输出。

5 仿真实验与分析

图2 组合导航的位置误差Fig.2 Position errors of integrated navigation

图3 组合导航的姿态误差Fig.3 Attitude errors of integrated navigation

根据仿真结果可以看出，将捷联惯导、重力匹配导航系统与气压高度计结合起来进行组合导航获得了较高的导航精度：水平位置精度达到±48.2 m，高度精度达到±11.5 m；航向精度达到±3.1′，水平姿态精度达到±1.6′，有效克服了捷联惯导系统误差随时间不断发散的缺陷。

与此同时，根据上述仿真结果还可以看出，本文中对Sage-Husa自适应滤波方程的改进取得了良好的滤波效果：在重力匹配导航系统输出非等间隔，而且每次间隔时间较长，甚至最大长达50 s的情况下，仍然保持着较高的组合导航滤波精度，组合导航的位置误差和姿态误差曲线均没有出现明显的跳变。可见，改进后的自适应滤波方程有效解决了重力匹配导航非等间隔输出和间隔时间较长易导致组合导航滤波精度降低的问题。

6 结束语

为了实现抗干扰性强、自主性好的高精度导航，本文研究了利用捷联惯导、重力匹配导航系统和气压高度计进行组合导航的方法。由于捷联惯导/重力匹配/高度计组合导航系统在工作时既不从外界接收信号，也不向外界辐射信号，仅利用了惯性、重力和大气压力等自然属性，是真正的强抗干扰性、完全自主隐蔽式导航系统，特别是能够适用于战场复杂电磁干扰等恶劣环境，在发射车、指挥车、装甲车等特殊军用车辆的导航定位领域中具有重要的军事价值和良好的工程应用前景。

参考文献：

[1] 于德新, 杨兆升, 刘雪杰. 基于卡尔曼滤波的GPS/DR导航信息融合方法[J].交通运输工程学报，2006, 6(2): 65-69.

YU De-xin, YANG Zhao-sheng, LIU Xue-jie. GPS/DR Navigation Data Fusion Method Based on Kalman Filter [J]. Journal of Traffic and Transportation Engineering, 2006, 6(2): 65-69.

[2] Cho Seong Yun, Choi Wan Sik. Robust Positioning Technique in Low-Cost DR/GPS for Land Navigation[J]. IEEE Transactions on Instrumentation and Measurement, 2006, 55(4):1132-1142.

[3] 陶俊勇, 温熙森, 杨定新, 等. 车载挠性SINS/GPS组合导航系统研究[J].中国惯性技术学报, 1999, 7(4): 16-19.

TAO Jun-yong, WEN Xi-sen, YANG Ding-xin, et al. Research on Flexible SINS/GPS Integrated Navigation System for Vehicle [J]. Journal of Chinese Inertial Technology, 1999, 7(4): 16-19.

[4] BISHOP G C. Gravitational Maps and Navigational Errors [J]. IEEE Journal Ocean Engineering, 2002, 27(3): 726-737.

[5] 程力, 蔡体菁. 航空重力匹配定位方法[J].中国惯性技术学报, 2007, 15(6): 698-701.

CHENG Li, CAI Ti-jing. Airborne Gravity Matching Locating Algorithm [J]. Journal of Chinese Inertial Technology, 2007, 15(6): 698-701.

[6] 程力, 蔡体菁. 基于支持向量机的重力匹配算法[J].系统仿真学报, 2008, 20(21): 5953-5956.

CHENG Li, CAI Ti-jing. Gravity Matching Algorithm Based on Support Vector Machine [J].Journal of System Simulation, 2008, 20(21): 5953-5956.

[7] 王志刚, 边少锋. 基于ICCP算法的重力辅助惯性导航[J].测绘学报, 2008, 37(2): 147-151.

WANG Zhi-gang, BIAN Shao-feng. ICCP Algorithm for Gravity Aided Inertial Navigation [J].Acta Geodaeica et Cartographica Sinica, 2008, 37(2): 147-151.

[8] 戴全发, 许厚泽, 许大欣, 等. 基于卫星测高数据的重力匹配导航仿真[J].武汉大学学报：信息科学版, 2008, 33(2): 203-207.

DAI Quan-fa, XU Hou-ze, XU Da-xin, et al. Simulation of Gravity Matching Navigation System [J].Geomatics and Information Science of Wuhan University, 2008, 33(2): 203-207.

[9] WANG Tang, HOWELL G, Tsai Yihsueh. Barometric Altimeter Short-Term Accuracy Analysis[J]. Aerospace and Electronic Systems Magazine IEEE, 2005, 20(12): 24-26.

[10] GRAY R A, MAYBECK P S. An Integrated GPS/INS/BARO and Radar Altimeter System for Aircraft Precision Approach Landings[C]∥IEEE Proceedings of the Aerospace and Electronics Conference, Dayton, 1995:161-168.

[11] 宫晓琳, 房建成, 盛蔚. 一种GPS与高精度气压高度表在线互标定方法[J].电子与信息学报, 2009, 31(4): 818-821.

GONG Xiao-lin, FANG Jian-cheng, SHENG Wei. A Method of Intercalibration for GPS and High Precision Baro-Altimeter on Line [J]. Journal of Electronics & Information Technology, 2009, 31(4): 818-821.

[12] 杨波, 王跃钢, 柴艳. 基于自适应滤波的飞艇组合导航系统研究[J].航天控制, 2010, 28(3): 33-37.

YANG Bo, WANG Yue-gang, CHAI Yan. Research on Integrated Navigation System for Airship Based on Self-adaptive Filter [J]. Aerospace Control, 2010, 28(3): 33-37.