飞行器末制导系统线角振动环境模拟试验技术*
苏华昌,姜虹,胡亚冰
(1.北京强度环境研究所,北京 100076; 2. 北京电子工程总体研究所,北京 100854)
0 引言
末制导控制系统是飞行器的核心和关键部分,在很大程度上决定着飞行器的性能,特别是制导精度。一些用于拦截的飞行器,为了实现高机动,采用脉冲发动机来产生所需要的控制力和力矩。通常飞行器是一个弹性体,在受到载荷作用时,就会引起弹体的弹性变形。在末制导过程中,发动机工作会给弹体造成较大的冲击力,除了产生控制所需的刚体姿态运动外,受飞行器结构弹性影响,还会导致较大高频弹体弹性线角振动环境。由于惯组和导引头敏感器件的感应,会将这些高频扰动引入控制系统,影响末制导系统的稳定性和精度,严重时会导致目标从导引头很小的瞬时视场中丢失[1-2]。
为了考核飞行器末制导性能,有必要对脉冲发动机工作带来的影响进行地面试验评估。目前,转台是测试导引头和惯性器件性能的有效工具,它能模拟弹体姿态角运动,通过实物仿真来测试导引头和惯组性能[3]。但是,由于转台带宽较低,不能模拟高频的角振动环境,而且转台承载能力有限,不能负载整个末制导弹体,无法考核结构弹性对控制系统的影响。另外,飞行器通常要进行线振动环境试验检验,由于没有叠加角振动环境,也难以真实检验末制导系统性能。为了合理对飞行器末制导系统进行性能检验,必须设计一个合理可行的地面模拟考核方案,准确模拟发动机工作带来的弹体动力学环境,通过地面试验来检验末制导系统的性能和精度,降低飞行风险和研制成本。
本文介绍了一种旨在考核脉冲发动机工作下末制导系统性能的模拟试验技术。首先,利用多维振动试验技术,设计了一个能实现进行线角振动联合加载的试验系统。然后,采用多维传递率矩阵和激励反推识别的方法,间接再现了线角振动时域响应波形;最后,通过地面数据和遥测数据的对比分析,对模拟的真实性进行了评估。
1 地面试验系统设计
飞行器在实际飞行中,承受的是六自由度振动环境,即3个方向线振动和绕3个方向的角振动同时存在。但受到试验设备水平的限制,早期只在单个振动台上进行单向的线振动环境模拟。随着电子技术的高速发展、振动控制理论的创新、多维振动试验系统的商业化出现,使得六自由度振动环境模拟变为可能,国外的一些重要航空航天动力学研究室已经开始了相关试验研究[4-7]。多维振动试验技术的出现,为使用电磁振动台来模拟角振动提供了技术支撑,电磁振动台带宽很高,能满足高频角振动模拟要求。在最新的美军标810G的多激励试验方法中,就明确提出了有关角振动概念和模拟方法。基于刚体运动学原理,可以通过2个振动激励设备,来构造图1所示的试验系统[8]。当2个激励设备同幅值同相激励时,可以实现z轴单纯线振动;当2个激励设备同幅值反相激励时,可以实现绕x轴单纯角振动。这2种形式称为多激励单轴试验形式(multi-exciter/single-axix,MESA)。当2个激励幅值和相位各自独立时,系统可以同时实现z轴线振动和绕x轴角振动,此形式称为多激励多轴试验形式(multi-exciter/multi-axis,MEMA),它为飞行器在试验室进行线角振动环境模拟提供了技术可行性。
地面模拟试验需要使用真实的力学环境,现有的惯组角速率和遥测点线振动环境,代表了飞行器跟踪目标过程中控制系统工作导致的弹体响应,模拟了该环境就实现了地面试验与飞行环境的高度相关。由于遥测环境呈典型的非平稳特征,最真实的办法就是直接进行时间历程再现。但是,要再现遥测的线角振动时间历程,存在几个难点。首先,遥测点虽然测量的是线振动,但不在弹体端面中心,响应存在着耦合,由于测量自由度不足,无法解耦。其次,遥测点与惯组不在弹体同一端面内,而且惯组角振动环境是减振后的角速率响应,带有非线性的减振器环节,大大增加了试验模拟的复杂性。最后,受多维波形复现试验技术的限制,目前很难直接通过响应控制的方式进行角速率时间历程复现。基于以上原因,不考虑直接去复现遥测位置的线角振动响应。
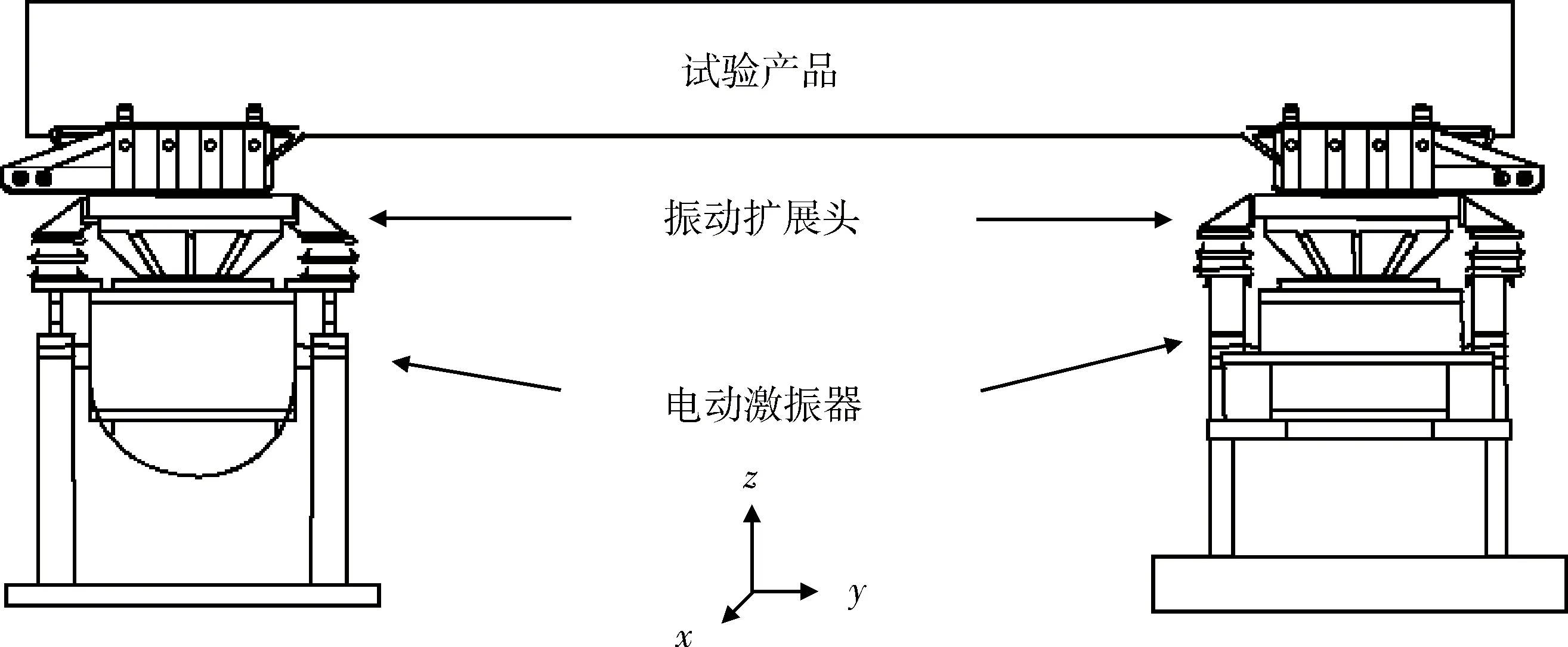
图1 MESA试验形式Fig.1 MESA test form
通过激励源分析,在末制导飞行过程中,弹体控制通过脉冲发动机来实现,弹体的力学环境主要是由发动机工作时的瞬态激励造成的,气动力影响很小,因此,可以通过振源模拟的方式来复现响应,只要振源模拟得比较准确,那么弹体线角响应就会得到准确再现。基于MEMA试验方法,设计了一套双台激励的试验系统,来进行线角振动联合加载模拟,系统如图2所示。该系统设计了一个特殊工装,工装底部两端分别连接2个振动台,工装上端与弹体发动机端面相连,来模拟脉冲发动机工作激励。
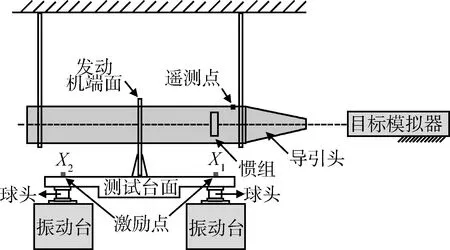
图2 末制导系统线角振动试验示意图 Fig.2 Linear and angular vibration test system for terminal guidance system
试验时,控制工装端面的2个激励点,可以通过调整激励大小和相位的变化来形成线振动和角振动,通过发动机端面传递给弹体,实现线角振动环境模拟。试验需要复现的2个响应在2个端面:一个是遥测点的线振动,一个是惯组的角速率响应。当使用2个激励时,输入输出的数目相同,其解是可以唯一确定,从而理论上可以通过2个激励点来模拟,来间接复现出所需的线角响应环境。为了检验飞行器性能,可在导引头前方放置了目标模拟器,试验前整个控制系统通电工作,进行目标对准,然后通过施加线角振动环境,检验导引头的跟踪稳定性和精度,并同时进行导航模拟,考核惯组和整个控制系统性能。
2 线角振动时域间接模拟方法
如果间接实现遥测线角环境时域波形复现,需要知道激励的时域波形,2个激励点的时域波形可以通过类似载荷识别的方法来获得。载荷识别是指在结构动态特性已知的情况下,通过测量的响应,反推出施加的激励载荷[9]。为了反推出激励,需要通过试验获得激励点与响应点之间的传递关系。由于激励和响应的数量超过了1个,属于多维激励试验范畴,需要引入多维传递率测量和激励推导方法。
2.1 多维传递率测量原理
对于一个时不变的线性系统,结构上各点之间总是存在一定的传递关系,可以通过随机振动试验来获得它们之间的传递率矩阵。在平稳随机激励条件下,假定2个振动台激励X分别为X1和X2,规定位置处的线角响应R分别为RL和RA,在频域可以得到[10]
即
R(f)=HRX(f)X(f),
(1)
式中:R(f)为响应的傅氏谱矩阵;X(f)为激励的傅氏谱矩阵;HRX(f)为传递率矩阵。
两边乘以输入X(f)的共轭转置,得到:
即
GRX(f)=HRX(f)GXX(f),
(2)
式中:GRX为激励与响应互谱矩阵;GXX为激励的自谱矩阵。
只要输入之间相不互关,则GXX可以求逆,从而可以求出传递函数矩阵为
HRX(f)=GRX(f)GXX(f)-1.
(3)
因此,通过多自由度激励,同时测量激励和需模拟位置的响应,则可以获得整个传递矩阵。
2.2 传递率矩阵测量
为了获得激励点与模拟点之间的传递关系,进行了全弹传递试验。在传递试验时,以工装上2个激励点的线振动为输入,以遥测点的线振动和惯组的角速率为输出,用双台激励的方式进行试验,通过式(3)来计算遥测点线振动和惯组角速率对激励点的多维传递率矩阵。由于激励基于试验传递率矩阵推导来得到,传递率矩阵测量的质量就显得尤为重要。试验测得的传递率矩阵如图3所示,可以看出,试验获取的曲线非常光滑,保证了激励推导的精度。
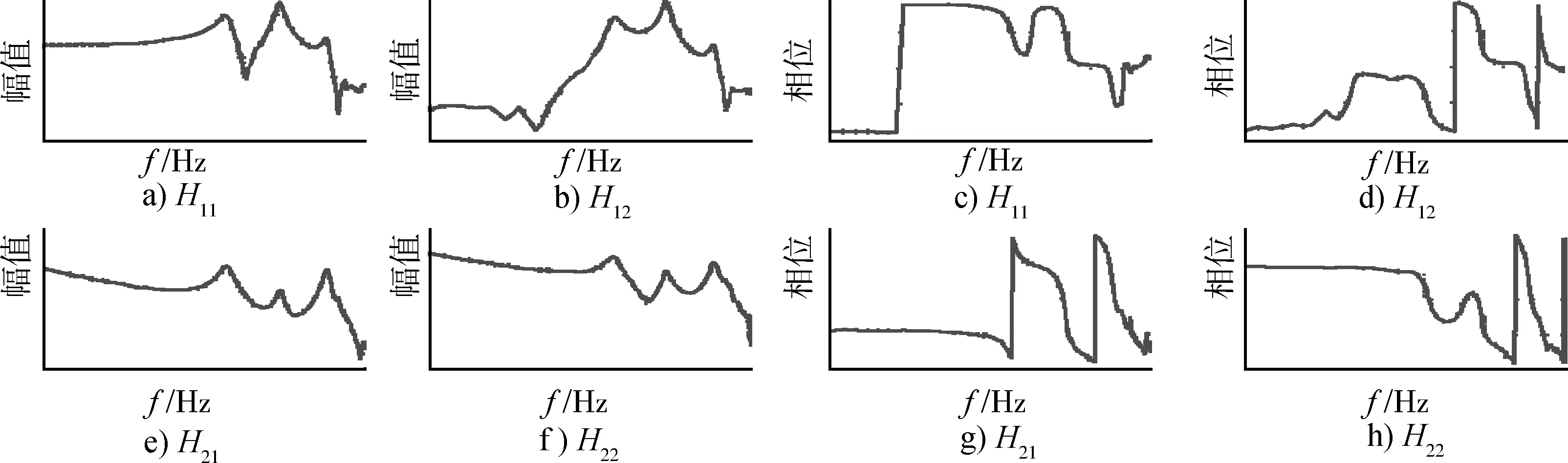
图3 传递率矩阵实测曲线Fig.3 Curves of transfer matrix on the spot survey
2.3 已知传递率矩阵和响应反推输入
在已知传递率矩阵HRX(f)和响应R(f)的情况下,通过式(1),可以反推出激励输入。假定需要模拟位置的线角自由度的时域响应分别为{rl(t),ra(t)},所需反推的线振动激励X的时域曲线分别为{x1(t),x2(t)}。由于R为发动机开关工作下的结构响应,呈现典型的瞬态特征。对于瞬态信号而言,激励和响应均非周期函数,绝对可积,满足狄利克雷条件,根据卷积定理,将激励和响应都转化到频域内,可得它们之间的关系为[11-12]
(4)
式中:BRX(f)为HRX的逆,由于线振动响应rl与角速率响应ra与激励x1和x2都有关。
由卷积定理可知,频域的乘积等于时域的卷积,使用卷积定理将式(4)转化到时域,可以得到
(5)
这样,使用需要间接模拟的时域数据,通过卷积的方式,就能直接得到激励的时间历程。
2.4 多维激励导出结果
利用2.3中的公式(5),对需要模拟的惯组角速率和遥测点线振动时域波形进行适当预处理后,结合传递试验获得的多维传递矩阵HRX(f),推导出了2个激励点的线振动时域波形,如图4所示。因为试验要复现线角振动环境,激励端面必然含有线振动和角振动2个自由度信息。对于多维振动时域波形再现,角振动自由度的信息通常以相干和相位的形式隐含在时域波形中,图5给出了2个激励点隐含的相干和相位信息。可以看出,为了间接实现所需的线角振动响应,2个输入激励的相干和相位是随频率变化的。获得激励的时域波形后,就能实现地面试验模拟。

图4 导出2个激励点时域波形Fig.4 Waveform on time domain of the two excitation point
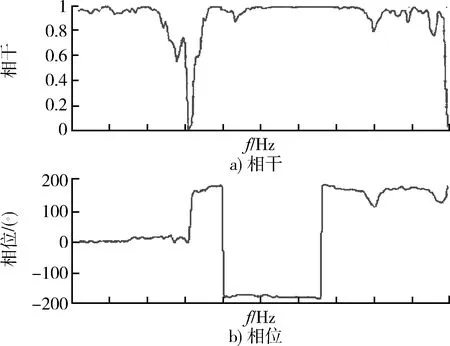
图5 激励之间的相干和相位关系Fig.5 Coherence and phase between the two excitations
3 模拟真实性检验
飞行器地面试验考核结果直接关系到其指标是否满足设计要求,因为线角振动环境通过间接方式来模拟,模拟的真实性对于性能评判非常重要,有必要对间接模拟的真实性进行检验。在试验时,控制仪只能对2个激励点的时域波形进行误差修正,不能直接修正间接模拟的线角响应,因此只能通过对试验响应数据分析来分析模拟精度,评估地面试验真实性。利用导出的2个激励点时域波形,对飞行器进行了线角振动波形复现调试试验,以检验地面试验模拟的真实性,检验从频域和时域2个方面进行。
3.1 频域内检验
将试验调试的实测响应处理成功率谱,与对应位置遥测信号功率谱进行对比,在频域内检验关键共振频率和整个谱密度曲线的一致性。试验调试与遥测结果的一致性越高,证明试验模拟越真实,图6给出试验调试和遥测原始结果的对比曲线。可以看出,在小量级下,模拟线角功率谱与遥测结果相差很小,各个主要的共振频率都得到了完全复现,试验模拟的精度非常高。在大量级情况下,模拟线角功率谱与遥测结果的主要特征也基本相同,只是高频段有一定放大,但是对于地面模拟考核来说,结果是保守的。放大主要是惯组减振器非线性造成的,因为模拟的角速率是减振后的响应,传递推导中包含了减振器特性,造成了一定的量级非线性。
3.2 时域内检验
受脉冲发动机的激励影响,遥测点的线振动时域波形具有很强的非平稳特性,以短脉冲波形的形式重复,这是此类导弹飞行环境的一个重要时域特征,因此,可以将地面模拟的遥测点波形和遥测结果进行相比对,检验其时域特性的相似性,作为地面试验模拟真实性的另一度量。图7给出了小量级调试时遥测点线振动的模拟对比曲线。可以看出,地面试验将脉冲发动机的瞬态激励进行了很好的模拟,完全复现了飞行环境的时域典型特征,证明试验模拟真实性很强。
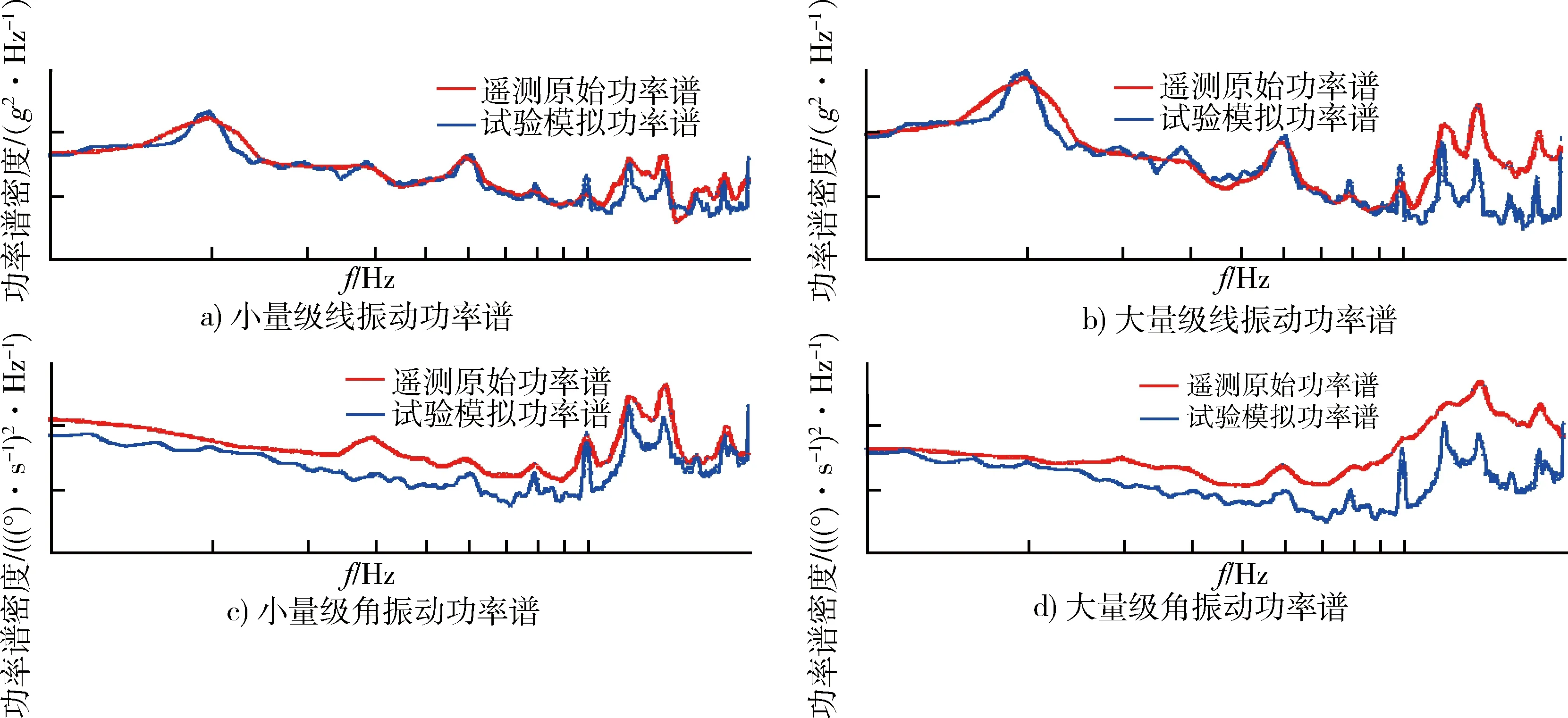
图6 试验模拟与遥测原始线角功率谱对比Fig.6 Comparison of linear and angular power spectral density between the test simulation and telemetric data

图7 遥测点模拟的时域特征对比Fig.7 Comparison of the test simulation and telemetric data in time domain character
4 结束语
(1) 本文利用多维振动试验技术,通过双台激励的方式实现了飞行器线角振动联合加载模拟。该试验方式克服了转台模拟带宽不足的缺陷,有效地模拟了弹体高频角振动,并同时施加了线振动环境,增加了地面试验的真实性。
(2) 基于遥测线角振动时域数据和测量的多维传递函数矩阵,反推出试验所需线振动激励条件,通过控制激励点的线振动时域波形,间接再现了飞行线角振动环境,解决了线角时域同时模拟的难题。
(3) 通过振源分析,选择了发动机端面作为激励传递端面,从而对飞行时发动机工作造成的弹体响应进行真实模拟。试验数据表明,遥测信号的各个主要共振频率都得到了很好复现,其时域模拟典型特征也非常相似,试验模拟真实性很好。
利用该项试验技术,成功对飞行器进行了地面试验模拟,考核了末制导系统的稳定性和精度,并检验了系统各部件的性能,取得了良好效果。该技术通过地面试验模拟对飞行器末制导系统进行系统级考核,提供了有效的地面研究手段,可以降低飞行试验风险和研制成本,该试验技术也可为其他飞行器末制导系统地面考核提供参考,具有较好的应用价值。
参考文献:
[1] 程云龙,丘淦兴,赵善友,等. 防空导弹自动驾驶仪设计[M]. 北京:中国宇航出版社, 1993.
CHENG Yun-long,QIU Gan-xing,ZHAO Shan-you,et al. Air Defense Missile Autopilot Design[M]. Beijing: China Astronautic Publishing House, 1993.
[2] David H Titterton, John L Weston.Strapdown Interial Navigation Technology Second Edition[M].Copublished by the Institution of Engineering and Technology,London,United Kingdom and the American Institute of Aeronautics,Reston,Virginia,USA:IEE©, 2004.
[3] 刘兴堂. 导弹制导控制系统分析、设计与仿真[M]. 西安:西北工业大学出版社, 2006.
LIU Xing-tang. Missile Guidance Control System Analysis, Design and Simulation[M]. Xi’an: Northwestern Polytechnical University Press, 2006.
[4] SMALLWOOD DAVID O.Multiple Shaker Random Vibration Control-An Update[C]∥Proceedings of the IEST,Ontario,California,USA,1999:212-221.
[5] STROUD R C,HAMMA G A,UNDERWOOD M A.A Review of Multiaxis Multiexciter Vibration Technology[J].Sound and Vibration,1996,30(4):20-27.
[6] UNDERWODD M A,KELLER T. Recent System Developments for MultiActuator Vibration Control[J].Sound and Vibration,2001,246(4):2-8.
[7] Alan Kenny. The Do’s and Don’ts of Multi-Shaker Testing[C]∥50th ATME of ESTCH,IEST,Las Vegas,Nevada,USA,2004: 274-284.
[8] MIL STD 810G, Department of Defense Test Method Standard [S].
[9] 傅志方. 振动模态分析与参数辨识[M]. 北京:机械工业出版社, 1990.
FU Zhi-fang. Modal Analysis and Parameter Identification [M]. Beijing: China Machine Press,1990.
[10] Cyril M Harris,Allan G Piersol. Harris' Shock and Vibration Handbook[M].5th ed.New York,USA:McGRAW-HILL,2002.
[11] Charles L phillips, John M Parr, Eve A Riskin.Signals,Systems,and Transforms,[M].3rd ed.Upper Saddle River, USA:Prentice Hall, 2003.
[12] Bendat, Julius S,Allan G Piersol. Random Data Analysis and Measurement Procedures [M].3rd ed.Hoboken,USA:John Wiley & Sons, 2000.

