基于直方图和脉冲关联的抖动信号分选算法*

陈维高，张国毅

(空军航空大学，吉林 长春 130022)

0 引言

雷达信号分选是获取敌方雷达信息从而判断其威胁等级、制定作战计划的主要依据，是雷达对抗系统的关键技术。其含义就是从多部雷达脉冲信号互相交迭的条件下，分离出属于同一部雷达的脉冲信号的过程[1]。可用于分选的特征参数一般包括射频(radio frequency,RF)、脉宽(pulse width,PW)、脉幅(pulse amplitude,PA)、脉冲重复间隔(pulse repetition interval,PRI)、到达角(direction of arrival,DOA)、脉内调制类型(modulation on pulse,MOP)[2]。其中PRI的变化样式最多，并且同一雷达信号的PRI具有严格的时间相关特性，因此只要区分出不同的PRI变化类型就可以完成信号分选任务。然而，在众多的PRI变化类型中，PRI抖动信号通过改变PRI值，削弱PRI间的规律性来达到抑制敌方电子干扰的目的，这样就给分选该类信号带来了巨大困难。因此，如何对PRI抖动信号进行准确率高、实时性好的分选，成为制约当前雷达信号分选发展的重要因素之一[3]。目前分选PRI抖动信号的典型方法是基于脉冲到达时间序列的复值自相关积分算法，即修正PRI变换法[4-5]，该算法将脉冲序列的TOA差值变换到一个PRI谱上，通过检测谱峰位置来估计脉冲序列的PRI值，并通过“交叠的RRI箱”和“可变的时间起点”来达到抑制谐波的目的，取得了较好的分选效果[6]。然而，该算法虽然能够很好地抑制虚假谐波，但运算量巨大，缺失了实时性，在当前高密度复杂信号环境下并不适用[7]。针对该算法在对抖动信号进行分选时存在的问题，本文提出了一种基于直方图和脉冲关联的抖动信号分选方法。算法首先通过直方图得到PRI(脉冲重复间隔)的统计值；然后利用累积判别判断是否进行下一级累积，对于不需要再进行累积的利用联通加权策略求得该PRI值；最后通过脉冲关联算法来抽取出该抖动信号的脉冲序列。

1 基于直方图的PRI测定原理

1.1 PRI抖动信号模型

在说明算法原理之前，首先介绍一下PRI抖动信号模型。PRI抖动信号是指相邻脉冲的PRI在一定范围内抖动，即相邻的脉冲时间间隔不相等，抖动范围一般小于PRI中心值的10%。PRI抖动调制的到达时间为

tn=tn-1+PRI0+δn+wn，

(1)

式中：PRI0为信号PRI的平均值；δn为第n个脉冲的抖动量；wn为非人为因素造成的随机抖动，可认为是随机噪声影响。

1.2 基于直方图的PRI测定

PRI抖动信号分选的难点之一就是PRI值的测定，该值测定的是否准确直接影响整个分选结果的准确度。本文测定PRI值的基本思想是：首先依据到达的抖动脉冲序列PRI值的范围划分小盒区间，对PRI值进行直方图统计，并利用累积判别判断是否需要进行下一级累积；然后设定一个容差范围，确定PRI值的代表区域，通过不同PRI值的代表区域确定邻近PRI；最后利用联通加权策略求得该PRI值，即为可能的抖动序列PRI值。

1.2.1 基本概念

定义1 PRI容差：针对抖动脉冲序列的PRI值设定一个容差ε，利用该容差值来确定PRI值的代表区域。

定义2 PRI值的代表区域：根据PRI容差可知每一个过门限PRIn(n=1,2,…，N)值的上下限为

(2)

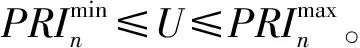
定义3 邻近PRI：如果2个PRI值的代表区域之间有交集，则称这2个PRI互为邻近PRI。

定义4 PRI小盒：为方便统计PRI的统计量和求得最后的PRI值，根据PRI值的范围划分PRI小盒，其大小为b。

定义5 PRI小箱：为方便说明，本文将邻近PRI对应小盒的集合称为PRI小箱。

1.2.2 累积判别

计算到达抖动脉冲序列的一级TOA差值，根据PRI值的范围划分PRI小盒，然后画出一级TOA差值直方图，此时需要进行累积判别来确定是否需要进行下一级的累积。

(1) 判断一级TOA差值直方图中是否存在过门限的PRI，若不存在过门限的PRI，则计算下一级TOA差值直方图并与第1级进行累积。

(2) 若只存在一个过门限的PRI，则不进行下一步的累积运算，直接选取该PRI值作为可能的抖动序列PRI。

(3) 若在多个辐射源出现时，可能在一级TOA差值直方图中存在多个过门限的PRI，但都不同于真实的PRI，则计算下一级差值直方图并进行累积。

1.2.3 子谐波检验

当存在大量脉冲丢失的情况下，真实PRI的谐波峰值在直方图中比较突出，可能存在谐波峰值超过门限而真实PRI并没有超过门限的情况，谐波将用于序列抽取中，造成分选错误。针对该情况，本文引入SDIF(sequence difference histogram)算法中的“子谐波检验”[8]来消除该弊端。“子谐波检验”过程如下：先找出直方图中最大值对应的PRI，若其低于门限，则检验超过门限的峰值对应的脉冲间隔，如果该脉冲间隔刚好是PRI的整数倍，则确定此脉冲间隔值为PRI的子谐波，以PRI进行序列抽取。

本文中直方图的检测门限函数为

Tthreshold(τ)=x(E-C)e-τ/kN，

式中：E为脉冲总数；C为差值直方图的级数；k为小于1的正常数；N为直方图上脉冲间隔的总值。常数x由实验确定。

函数的选取原因见文献[9-10]，此处不再赘述。

1.2.4 联通加权策略

由于本文针对的是相邻脉冲时间间隔不相等的PRI抖动序列，其脉冲时间间隔的波动程度随抖动量的大小而变化，所以在进行直方图统计时，一部辐射源的信号会分布在邻近的若干个PRI小盒中，这就影响了PRI值的测定。为解决该问题，得出最优的PRI测定值，本文提出了联通加权策略。

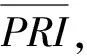
(3)

式中：S为互为邻近PRI的pri1,pri2,…，prin对应的累积量总和；xi为互为邻近PRI的单个prii对应的累积量。

2 脉冲关联抽取算法

在得到PRI测定值之后，下一步就是对脉冲序列进行抽取，进而分选出属于该辐射源的脉冲序列，本文引入一种脉冲关联算法[11]来完成序列抽取的任务。该算法以重频直方图分析为基础，对PRI测定值对应的脉冲对序号集进行记录，利用时差脉冲对之间的关联性实现脉冲序列的抽取。分布在第k个PRI小箱内的脉冲对序号集可表示为

Pk={(m,n),tn-tm∈Uk}，
1≤m

(4)

式中：K为PRI小箱的个数；(m,n)为脉冲对序号；Uk为第k个PRI小箱所包含的PRI小盒的集合；Pk为参与关联的脉冲对序号集。

下面通过实例来详细说明脉冲关联抽取算法。图1中实线表示PRI均值为300 μs，抖动量为10%的一部重频抖动雷达的11个脉冲，则U=[270,330]μs，其中脉冲7与脉冲8之间丢失了一个脉冲。虚线表示干扰脉冲，其中脉冲9，11之间和脉冲13，15之间的时差都在真实脉冲重复间隔的抖动范围内，即t11-t9∈U，t15-t13∈U。该脉冲序列在真实PRI抖动范围内的累积直方图如图2所示。

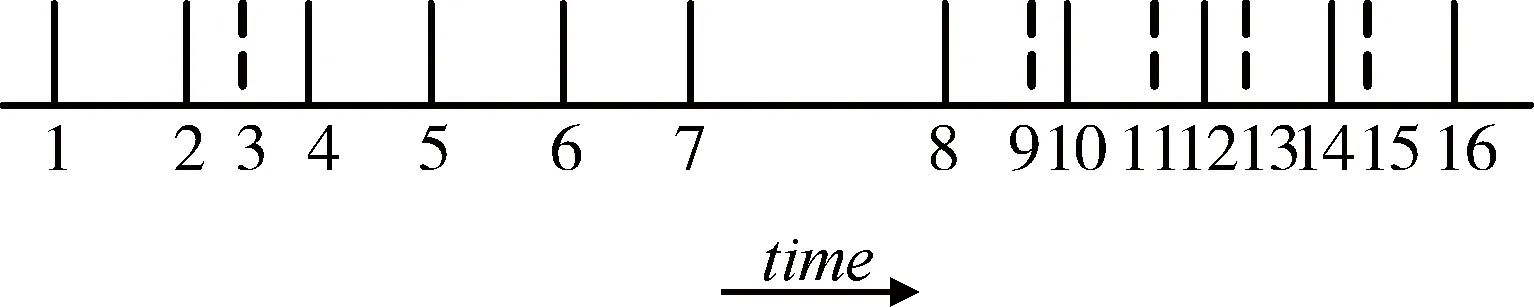
图1 PRI抖动脉冲序列示意图Fig.1 Diagram of PRI jitter pulse sequence

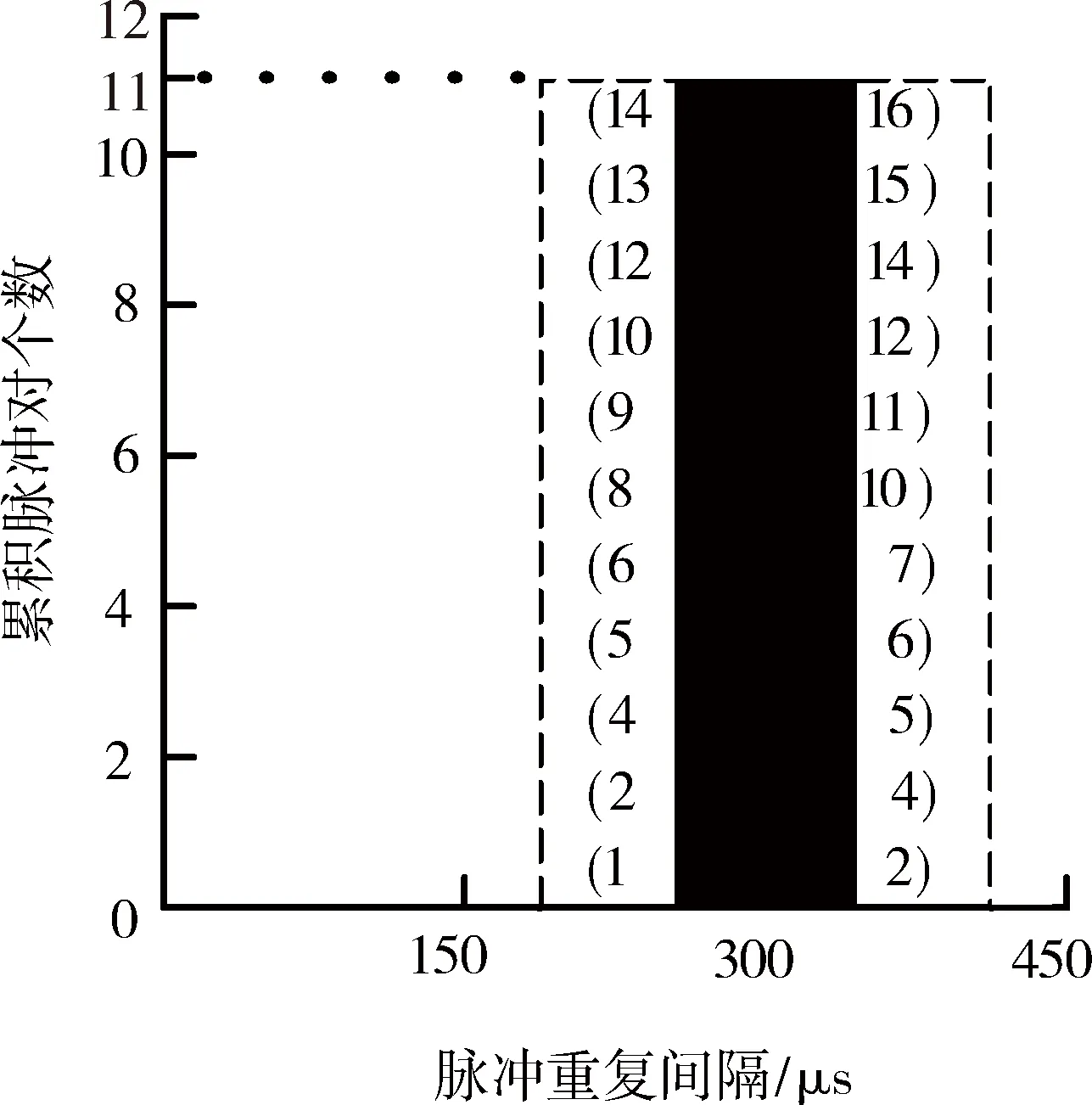
图2 重复间隔均值为300 μs的累积直方图Fig.2 Cumulative histogram which PRI is 300 μs

图2中虚线框内表示的是所有时差满足tn-tm∈U的脉冲对的脉冲序号，共有M=11对脉冲。其中，将第1列的脉冲序号集用PL表示，第2列的脉冲序号集用PR表示，可以建立第1列与第2列的脉冲序列数学模型为

(5)

(6)

gL(t)和gR(t)的互相关函数可表示为

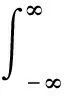
(7)

C(0)即对应了脉冲序列关联的结果，在本例中为“关键脉冲序列”{2,4,5,6,10,12,14}。对该序列进行一阶差分运算，进行漏脉冲检测，由于脉冲6与脉冲10之间间隔较其他的相差较多，知其中间存在漏脉冲，可以将脉冲7与脉冲8“补”回来。另外，在“关键脉冲序列”的首尾处应该各有一个脉冲，同样“补回来”，即本例中的脉冲1和脉冲16。最终可抽取出完整的脉冲序列{1,2,4,5,6,7,8,10,12,14,16}，而干扰脉冲在相关运算过程中自然被过滤掉了。由于PRI抖动脉冲序列的脉冲重复间隔存在波动，在统计直方图时较常规脉冲序列更容易受到干扰脉冲的影响，但干扰脉冲之间没有关联性，所以利用脉冲关联抽取算法可以很容易地将干扰脉冲剔除，并且几乎是在形成直方图分析的同时将该脉冲重复间隔对应的脉冲序列抽取出来。

3 分选算法基本步骤

利用基于直方图和脉冲关联对重频抖动信号进行分选包括两大步骤：①基于直方图的PRI测定；②利用脉冲关联算法对抖动序列进行抽取。分选算法的基本步骤描述如下：

(1) 计算抖动脉冲序列的一级TOA差值，根据PRI值的范围划分PRI小盒。

(2) 进行一级差值直方图统计和累积判别，对于不需要累积的转入步骤(3)，需要累积的转入步骤(4)。

分选算法的流程如图3所示。

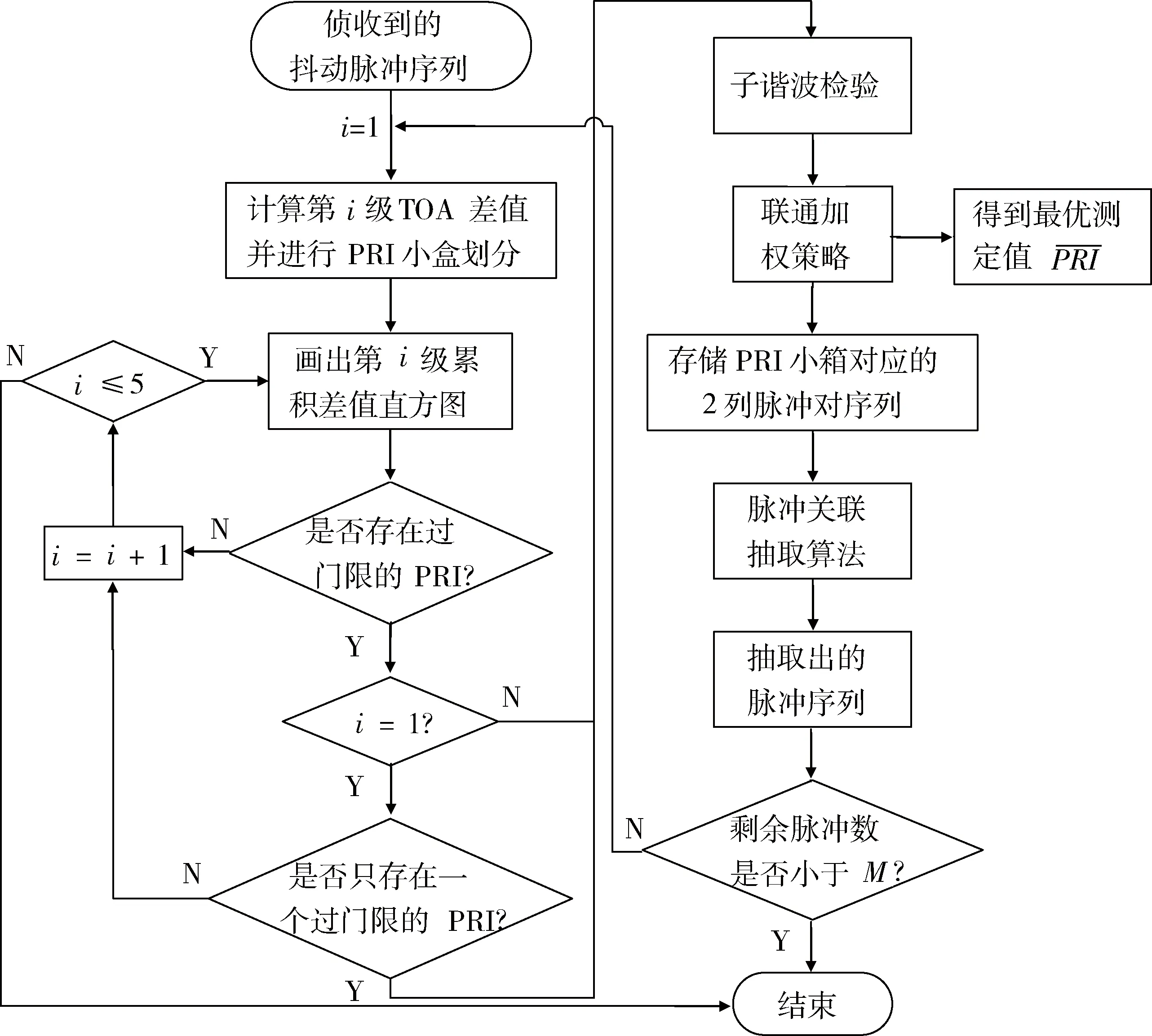
图3 算法流程图Fig.3 Algorithm flow chart

4 仿真实验分析

实验采用的仿真平台为Intel CPU Q8200，3GB内存，操作系统为Windows XP，仿真软件为Matlab R2010a。在介绍实验之前，为了评价分选效果首先明确2个概念：①分选准确率：(SR/S)×100%，其中S为分选得到的同一类脉冲的个数，SR为正确分选的脉冲数；②漏选率：((SM-SR)/SM)×100%，其中SM为原始脉冲序列中属于同一辐射源的脉冲个数[12]。为了验证算法对重频抖动信号分选的有效性和对干扰脉冲的识别能力，以及抗脉冲丢失能力，本文进行了以下实验。

(1) 实验选用3部重频抖动雷达形成的交叠脉冲序列作为原始侦收到的脉冲序列，实验中存在2%的脉冲丢失并加入10%的干扰脉冲。3部重频抖动雷达的数据信息如表1所示。

利用本文算法对上表中的实验数据进行分选，形成的累积直方图如图4所示。

表1 辐射源数据信息表Table 1 Source data information table

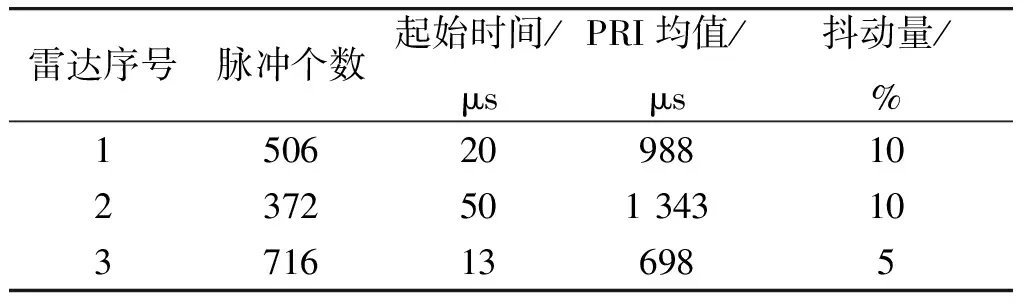
雷达序号脉冲个数起始时间/μsPRI均值/μs抖动量/%150620988102372501 343103716136985

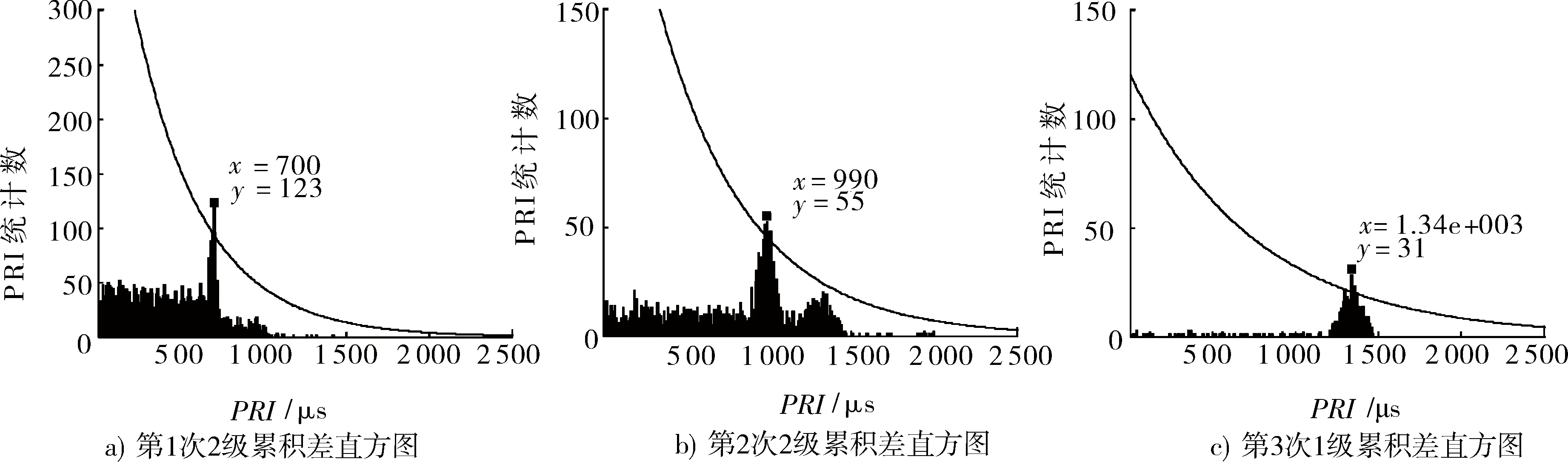
图4 分选得到的累积TOA差值直方图Fig.4 Cumulative histogram of signal sorting

表2 分选结果统计表

Table 2 Statistics data of sorting results

雷达序号PRI均值/μs脉冲个数PRI测定值/μs分选出脉冲个数正确分选个数准确率/%漏选率/%1988506991.546845890.59.4921 3433721 348.334032487.112.903698716699.267466793.26.84统计1 5941 4821 44990.99.74

(2) 从表2的统计结果可以看出，算法较准确地测定出了PRI值，PRI测定值的平均相对误差为0.307%，利用脉冲关联对脉冲序列进行抽取的平均准确率为90.9%，平均漏选率为9.74%，验证了该算法能够较好完成对多部重频抖动交叠信号的分选任务，并且具备一定的抗干扰和抗脉冲丢失能力。为了进一步验证算法分选PRI抖动调制信号的能力，本文利用传统的改进PRI变换算法处理相同的实验数据，仿真环境相同，图5是利用该算法得到的PRI测定值。图6是分别利用2种算法对只含有雷达1的脉冲序列进行分选，通过100次Monte Carlo仿真实验，统计得到的2种算法的平均时间消耗对比图。

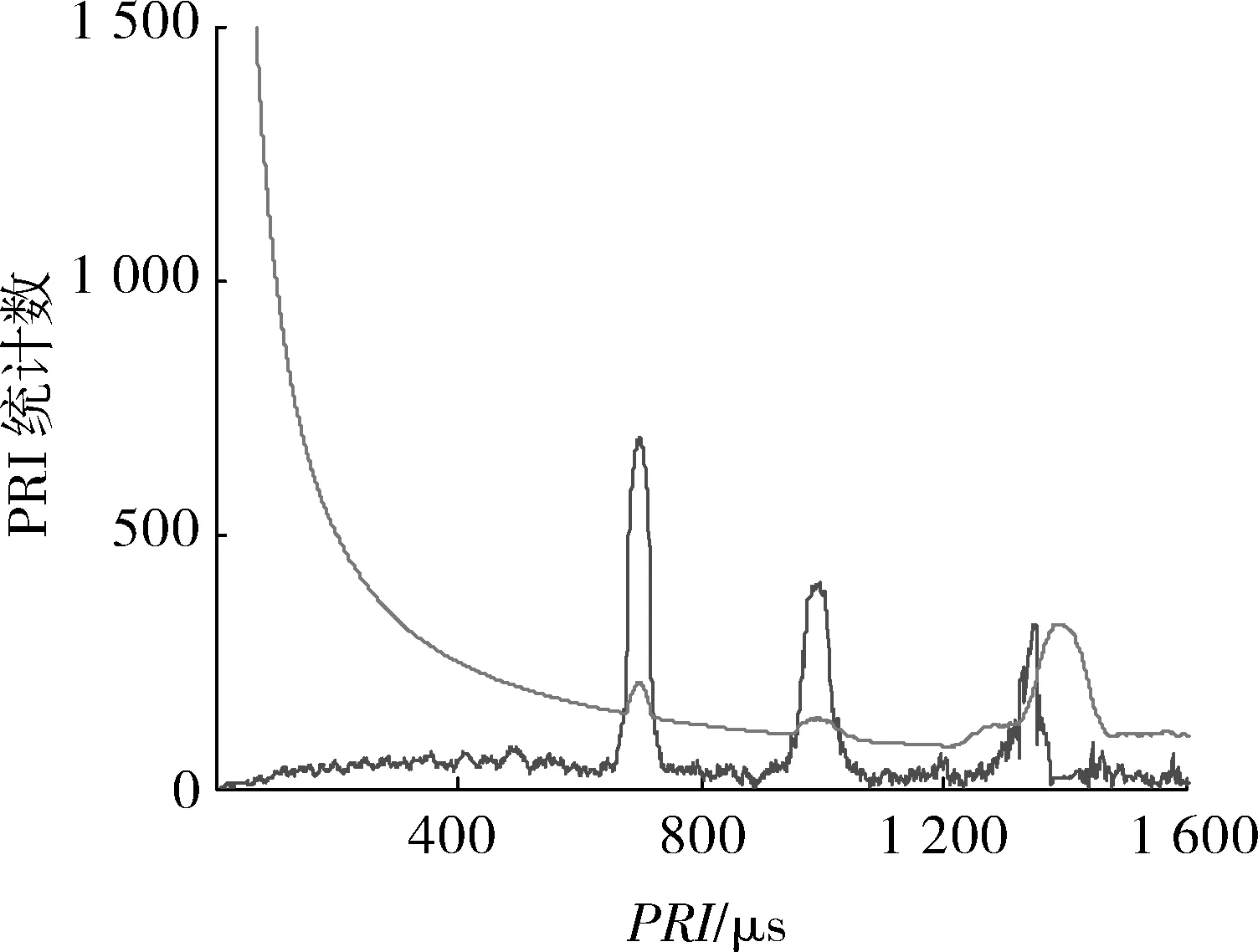
图5 修正PRI变换算法仿真图Fig.5 Simulation diagram of modified PRI transform

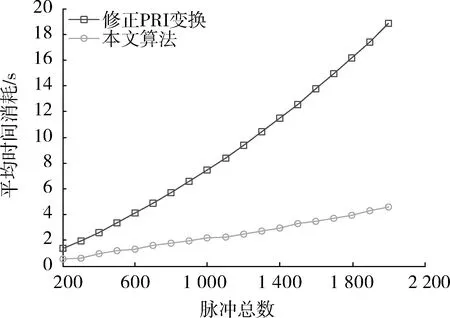
图6 平均时间消耗对比图Fig.6 Diagram of average time consumption

从上述2幅图中可以看出，利用修正PRI变换算法能够得到该组实验数据的PRI测定值，其平均相对误差为0.314%，与本文算法得到的PRI值大致相同，但修正PRI变换的时间消耗随脉冲总数的增长急速增加，而本文算法的时间复杂度较低，随脉冲总数的增加较缓慢，算法的执行效率较高。在分选准确率上由于修正PRI变换算法利用传统的抽取算法，错误分选和漏分选脉冲数较多，而本文算法利用了脉冲关联对脉冲序列进行抽取，得到了较高的分选准确率。

5 结束语

本文在分析了当前抖动信号分选面临主要问题的基础上，提出了一种基于直方图和脉冲关联的抖动信号分选算法。该算法在直方图统计的基础上利用累积判决和联通加权策略求得最优的PRI测定值，然后通过脉冲关联抽取出抖动脉冲序列，在保证PRI测定和分选准确性的基础上，提高了分选的实时性。通过仿真验证，证实了该算法在保证PRI估计准确度的基础上，提高了分选的准确率和实时性，并且具备一定的抗脉冲干扰和脉冲丢失的能力。其综合性能优于现有其他抖动信号分选方法，具有较好的工程应用价值。

参考文献：

[1] 何明浩．雷达对抗信息处理[M]．北京：清华大学出版社，2010：8-9．

HE Ming-hao. Radar ECM Information Processing[M]. Beijing: Tsinghua University Press, 2010: 8-9.

[2] 普运伟．复杂体制雷达辐射源信号分选模型与算法研究[D]．成都：西南交通大学，2007:10-12．

PU Yun-wei. Deinterleaving Models and Algorithms for Advanced Radar Emitter Signals[D]. Chengdu: Southwest Jiaotong University, 2007:10-12.

[3] XIE Guo-liang, WANG Hong-xun, XU Zhong-wei,et al. A Fast Sorting Method for Modulated and Jitter PRI Radar Signals[C]∥Transportation, Mechanical, and Electrical Engineering (TMEE), 2011 International Conference on,Changchun,2011: 2210-2213.

[4] Ala Mahdavi, Amir Mansour Pezeshk. A Fast Enhanced Algorithm of PRI Transform[C]∥Sixth International Symposium on Parallel Computing in Electrical Engineering,Luton, 2011: 179-184.

[5] TIAN Fen-fang. De-Interleaving of Radar Signal Based on Improved PRI Transform Algorithm[J]. Electronic Science and Technology，2010, 23(11): 116-118.

[6] 李峰．复杂环境下雷达辐射源信号分选算法研究[D]．西安：西安电子科技大学，2009：32-39．

LI Feng. Research on Algorithms for Radar Emitter Signal Sorting in Complex Environments[D]. Xi’an: University of Electronic Science and Technology, 2009: 32-39.

[7] 张秀辉．密集信号环境下信号分选算法研究与应用[D]．无锡：江南大学，2009：7-8．

ZHANG Xiu-hui. Study and Implementation of Signal Sorting Algorithms for Complex Environments[D]. Wuxi: Jiangnan University, 2009: 7-8.

[8] 向娴．未知雷达信号分选算法研究[D]．西安：西安电子科技大学，2011：15-16．

XIANG Xian. Research of Unknown Radar Signal Sorting Algorithm[D]. Xi’an: University of Electronic Science and Technology, 2011: 15-16.

[9] MILOJEVIC D J, POPOVIC B M. Improved Algorithm for the Deinterleaving Radar Pulses[J]. IEE Proceedings, Part F: Radar and Signal Processing, 1992, 139(1): 98-104.

[10] 王宇．未知雷达信号PRI的快速分选识别算法研究[D]．西安：西安电子科技大学，2010：29-32.

WANG Yu. Research on Rapid Algorithm for Sorting and Identification of Unknown Radar Signal[D]. Xi’an: University of Electronic Science and Technology, 2010: 29-32.

[11] 李腾．基于脉冲关联的雷达信号重频分选算法[J]．电子信息对抗技术，2007，22(1)：10-13．

LI Teng. Radar Pulse PRF Deinterleaving Algorithm Based on Pulses’ Relativity[J]. Electronic Information Warfare Technology, 2007, 22(1): 10-13.

[12] 樊甫华，张万军，谭营．基于累积变换的周期性对称调制模式的快速自动搜索算法[J]．电子学报，2005，33(7)：1266-1270．

FAN Fu-hua, ZHANG Wan-jun, TAN Ying. A Fast and Automatic Searching Algorithm of Periodic and Symmetric Patterns Based on Accumulative Transformation Technique[J]. ACTA Electronica Sinica, 2005, 33(7): 1266-1270.