防空作战战场抢修保障资源配置地域选择模型*
程汉文,黄立坡,蒋里强
(防空兵学院,河南 郑州 450052)
0 引言
武器装备的战场抢修,是指战时对损坏的武器装备在损坏地或者就近进行修理。它是战时技术保障工作中十分重要的内容,是迅速恢复武器装备战斗力的主要措施。但是,战时有限的资源在一定程度上制约战场抢修活动的开展。需要通过战时资源优化管理,将战时所需的人力、器材、保障装备、技术、信息及时间等各种资源,以装备的完好性和作战使用需求状态为中心,配置到发挥最大效用的位置[1]。
现代防空作战中,在抗击空中目标的同时,防空兵自身安全亦更为重要,防空兵装备维修保障资源的配置要力求纵深、疏散、隐蔽,便于保障,利于安全[2]。针对防空作战的特点,合理选择维修保障资源配置地域,从而加快维修保障资源输送速度,迅速完成战场抢修,最大限度地恢复武器装备的战斗力,对完成防空作战任务有重要的意义。
战场抢修资源管理可以看成应急系统的管理问题。从应急管理角度研究应急资源配置,已有成果不少,但一般都是针对灾害、疫情等问题展开[3-8],而涉及军事背景的研究不多,至于针对防空作战的研究更为少见。由于战时战场抢修资源配置与民用应急资源保障有很大不同,一切问题均需要围绕军事目的的实现考虑设计,军事需要超过经济意义[9],时间既是首要目标因素,同时还是条件因素。特别是在防空作战中,要充分考虑空袭间隔时间对战场抢修任务的影响。因此,有必要对针对这种特殊要求的资源配置问题进行研究。
本文对防空作战中保障资源配置地域的选择问题进行了探讨,利用可靠性理论,以作战需求为目标定义了战场抢修的允许等待时间,并给出了计算方法,以此为基本约束条件,建立了非线性规划模型用于保障资源配置地域的选择。
1 战场抢修等待的允许时间
1.1 战场抢修的等待时间
战时情况下,为了保证作战任务的顺利进行,在保障物资、人员、体制等各方面都最大限度地给予满足,因此战场抢修中的延误时间主要受到保障资源输送到武器装备损坏地时间的影响,在此将它称为战场抢修的等待时间,显然,它是维修保障资源配置地域选择主要考虑的条件。而维修保障资源配置地域接近防空阵地,可以尽可能地缩短战场抢修的等待时间。但是,防空作战对装备维修保障资源的配置地域要求一定纵深,利于机动、隐蔽,从一定意义上远离防空阵地将有更好的安全性。所以考虑战场抢修等待的允许时间,在尽可能不影响战场抢修的情况下,选择装备维修保障资源的配置地域。
1.2 战场抢修等待的允许时间
战备完好率表示当要求装备投入作战时,装备准备好能够执行任务的概率[10]。作为既定任务,装备完好率必须满足一定要求,因此将其作为作战需求即衡量是否能够完成作战任务的一个基本指标。定义战场抢修等待的允许时间就是满足一定战备完好率条件下战场抢修等待时间的允许值。
现代防空作战,空袭强度大大加强,战斗中战损装备增多,作战任务间隔时间缩短,一次作战任务后,执行新任务时的装备作战能力应包括以下因素:武器装备的战损情况,武器装备的修复能力,任务间隔时间,维修资源的保障能力等。在这种情况下,建立装备的完好率模型为
Por=1-Q+QP(tm (1) 式中:Q为装备上次防空作战的损坏率,一般包括2项:战斗损伤和随机故障;tm为装备的修理时间;tn为下次任务开始时间,防空作战中可以用敌空袭的间隔时间;tw为延误时间,在此只考虑战场抢修的等待时间;P(tm (2) (3) 还假定空袭兵器进入为参数λ的泊松流,则空袭兵器到达间隔时间即下次任务下达前时间服从指数分布 n(tn)=λexp(-λtn). (4) (5) 此时, 将其代入式(1)可以得到 (6) 式中: 式(6)的含义是满足作战任务要求,即战备完好率达到目标值时,装备维修平均等待时间。所谓战备完好率的目标值是指根据作战任务需要,为保证完成作战任务,武器装备所必须具备的投入作战的能力。在此要求下,平均等待时间须满足式(6),显然当平均等待时间大于式(6)确定的值时,将影响战损装备的修复,战备完好率达不到目标值;当平均等待时间小于式(6)确定的值时,赋予战损装备更多的修复时间,在下次任务下达前,修复的装备越多,战备完好率越高。因此,用式(6)确定的平均等待时间作为选择维修保障资源配置地域的指标,作为战场抢修等待的允许时间。 其中,式(6)中分子即 (7) 注意式(6)由指数分布导出,对于其他分布利用式(1)和式(2)通过数值解法也可以得到战场抢修允许时间。实际应用中,一次任务后装备的战损情况和资源需求可以通过以往经验估计得到。当然,考虑上述各种随机因素,基于此模型通过统计模拟方法也是可行的,基于主题,不在此讨论。 由于防空作战地域位于我方内部,可以根据战术要求先选取多个地域作为备选,因而可将问题简化,即从备选地域中选择保障资源配置地域。战时,便于保障属性指标可以用时间来衡量,即在选择时,其输送维修保障资源时间应小于战场抢修等待的允许时间。当然最简单的是选择配置地域时,可以使其到达各阵地的时间都小于战场抢修等待的允许时间,但这是不现实的,因为其受到防空阵地配置条件限制,防空阵地的配置很分散的话,这样的选择可能不存在,并且即使可行,可能造成保障资源过分集中,其本身成为重要目标而易受到攻击。所以据此,建立如下模型。 (1) 设有防空武器装备分布于n个防空阵地,有m个待选的维修保障配置地域,保障资源有l种。 模型表示如下: (8) 上述模型类似于资源调度模型可以作为最短时间最大流问题求解[11],但算法比较复杂。为此本文通过将问题转化为线性规划,给出一种简便算法求解,以满足战时适时性需要。引进函数 (9) (10) 注意到上述目标是保证输送时间最大的路径所花时间最小,而实际中一般还要求保障分队出动越少越好,因此考虑所有路径花费时间总和最小,目标函数改为 (11) (12) 上述处理后,模型转换为线性规划问题,而线性规划求解已有成熟的算法[12],简单快捷。 假设某种装备要求首次投入战斗的战备完好率要达到95%,其火控系统平均修复时间为0.458 6 h,假设敌空袭兵器平均间隔0.5 h来袭一次,火控系统位于车体内部,除非直接受到攻击,否则以随机故障为主,一次战斗后火控系统战损率为10%,通过式(6)可以算出该武器火控系统战场抢修等待的允许时间为12 min。 现有3个防空阵地、7个待选维修资源配置地域,待选维修资源配置地域输送物质到阵地时间见表1,装备战场抢修需要2种维修资源,设一次任务后3个阵地2种资源的需求量见表2,为安全起见,各待选配置地域2种资源储备分别不超过4和8。 表1 待选地域向防空阵地输送物质时间Table 1 Transportation time from candidate location to air defense positions min 表2 3个阵地2种资源的需求量Table 2 Resources demand of air defense positions 算例中看到可以有多种配置地域选择方案供决策者选择,而且均满足允许时间要求。由于实际作战中,时间都是随机变量,而考虑平均时间作为允许时间,因此,实际应用中还应有一定的冗余量,本例中,根据计算结果,2和6号可以都作为选择地域,而3和4号不考虑。当然,最终还是要根据战时实际时间处理战场抢修保障资源,但这已属于战场资源调度的问题了。实际上,战场资源管理包括配置和调度2个环节,配置是基础,而战场抢修需要通过资源调度来实现。 本文从满足一定战备完好率出发,考虑武器装备系统的维修和敌空袭规律,引进战场抢修允许时间,作为战场抢修保障资源配置地域的选择依据,建立了规划模型用于保障资源配置地域的选择。 整个模型分为2个部分:第1部分战场抢修允许时间的确定,其中式(6)由指数分布导出,对于其他分布利用式(1)和式(2)通过数值解法也可以得到战场抢修允许时间。其他情况,可以根据实际作战积累的数据或统计模拟方法来处理。第2部分维修资源配置地域选定,经过简化规划模型计算较为简单,适合战时决策时间要求。并且对其他作战资源配置也可提供参考。 本模型仅考虑防空作战中一些主要因素,对更为复杂的情况,例如不同保障单位的优先权等问题,还需进一步完善。另外模型假定保障资源充足,但随着战斗时间延长资源量也是要考虑的问题,此种情况下配置模型还蕴含了保障资源种类和量的预测,这对于防空作战具有更重要的实际意义,是下一步研究的重点。 参考文献: [1] 陈希林,肖明清,王学奇. 国内外战场抢修研究的现状和发展[J]. 兵工自动化,2006,25(9):14-17. CHEN Xi-lin, XIAO Ming-qing, WANG Xue-qi. Status and Development of Research on BDAR both in China and Abroad[J]. Ordnance Industry Automation, 2006, 25(9): 14-17. [2] 武文军,刘军,唐兴诚. 防空兵部队战术[M]. 北京:军事科学出版社,2001. WU Wen-jun, LIU Jun, TANG Xing-cheng. Air Defense Forces Tactics[M]. Beijing: Military Science Press, 2001. [3] 周光亮. 应急资源配置与调度文献综述与思考[J]. 预测,2011,30(3):76-80. ZHOU Guang-liang. Review and Perspective of Emergency Resources Allocation and Scheduling[J]. Forecasting, 2011, 30(3): 76-80. [4] BASAR A, CATAY B, UNLUYURT T. A Taxonomy for Emergency Service Station Location Problem[J]. Optimization Letters, 2012, 6(6): 1147-1160. [5] REVELLE C S, EISELT H A, DASKIN M S. A Bibliography for Some Fundamental Problem Categories in Discrete Location Science[J]. European Journal of Operational Research, 2008, 184(3): 817-848. [6] ARABANI A B, FARAHANI R Z. Facility Location Dynamics: An Overview of Classifications and Applications[J]. Computer and Industrial Engineering, 2012, 62(1): 408-420. [7] VALLIM A, MOTAL I. Optimization Models in the Location of Healthcare Facilities a Real Case in Brazil[J]. Journal of Applied Operational Research, 2012, 4(1): 37-50. [8] ALI O, KIAT C T, BOON H O, et al. Location and Routing Models for Emergency Response Plans with Priorities[C]∥Proceeding of 7th Security Research Conference, Berlin: Springer, 2012: 129-140. [9] 杨德珍,章文晋. 装备保障资源配置问题及发展[J]. 物流科技,2008,31(4):106-109. YANG De-zhen, ZHANG Wen-jin. Most Optimum Distribution of Military Logistics Resources[J].Logistics Sci-Tech, 2008, 31(4): 106-109. [10] 康锐. 可靠性维修性保障性工程基础[M]. 北京: 国防工业出版社, 2011. KANG Rui. Fundamentals of Reliability & Maintainability & Supportability Engineering[M]. Beijing: National Defence Industry Press, 2011. [11] 曹继平,宋建社,朱昱,等. 战场抢修多需求点多资源优化调度研究[J]. 兵工学报,2008,29(8):995-1000. CAO Ji-ping, SONG Jian-she, ZU Yu, et al. Research on Battlefield Maintenance Optimization Scheduling of Multi-Requirement-Point and Multi-Resource[J]. Acta Armamentarii, 2008, 29(8): 995-1000. [12] 蒋里强,左军. 防空作战模拟方法概论[M]. 北京:海潮出版社,2010. JIANG Li-qiang,ZUO Jun.Introduction to Air Combat Simulation[M].Beijing:Haichao Press,2010.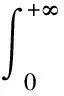
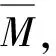
2 战场抢修保障资源配置地域
2.1 战场抢修保障资源配置地域选择模型

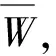
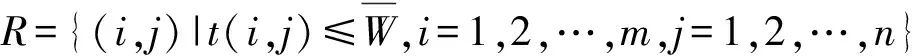
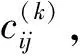
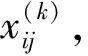
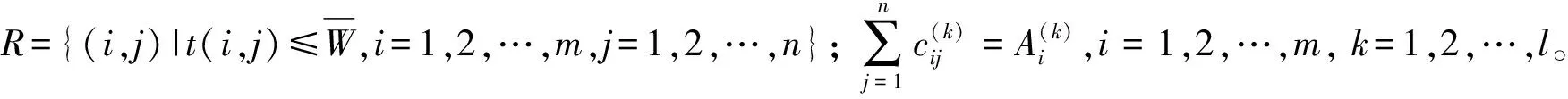
2.2 模型求解

3 算例


4 结束语
——国外课堂互动等待时间研究的现状与启示

