分布式多假目标干扰下组网雷达检测性能分析*
房明星,王杰贵,杨永晶
(电子工程学院,安徽 合肥 230037)
0 引言
如何评价雷达组网系统在干扰环境下的检测性能是雷达电子战研究的热点问题之一。当前,不少学者都对干扰情况下组网雷达检测性能进行了研究。文献[1]建立了压制干扰条件下雷达组网检测概率模型。文献[2]研究了多假目标干扰对雷达检测性能的影响。文献[3]基于分布式检测完整推导了组网雷达系统检测概率的数学模型。它们研究的侧重点虽不同,但均没有对分布式多假目标干扰下组网雷达的检测性能进行研究。因此,本文首先从分布式多假目标对组网雷达干扰出发,进而研究了多假目标干扰对雷达网恒虚警率(constant false alarm rate,CFAR)处理的影响,最后根据Albersheim 的经验公式[4-5]建立了一个适用于非起伏目标的雷达网检测概率计算模型,并提出了一种衡量雷达网综合检测性能的评估指标,最后对模型进行了仿真,并给出了相应的结果分析。
1 对组网雷达的分布式多假目标干扰原理
1.1 分布式多假目标干扰原理
分布式干扰是指将多部小型干扰机分布在特定的空域、地域上,这些干扰机通过控制中心统一协调,相互之间有机配合,从而对雷达或者组网雷达实现一种“面对面”的干扰,多部干扰机组成了能力更强的干扰体系,这种干扰方法具有分布面广,干扰距离近的特点。
分布式小型干扰机主要采用多假目标干扰及灵巧噪声干扰。因而分布式多假目标干扰就是在对雷达进行分布式干扰时所采取的假目标干扰。
1.2 多假目标产生方法
本文针对LFM(linear frequency modulation)脉冲雷达,利用数字射频存储技术(digital radio frequency memory,DRFM)来产生多假目标干扰信号。DRFM技术是目前已知能实现脉内信号相干调制、存储和转发的有效手段,DRFM产生的干扰信号可视为是截获雷达信号的相干复制品,能够对雷达实现相干干扰,可以达到降低干扰所需功率、增强干扰效果的目的。利用DRFM产生假目标干扰信号主要是对接收到的雷达信号进行距离时延和多普勒移频。
(1) 假目标距离时延量
假设雷达发射信号的脉冲重复周期为Tr,雷达与干扰机的距离为R0,假目标与雷达距离为Rf,τ为雷达脉冲到干扰机的时延,Δτ为干扰机转发雷达信号的时延,则假目标的距离时延有如下关系:
(1)
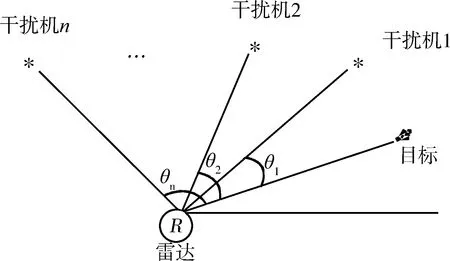
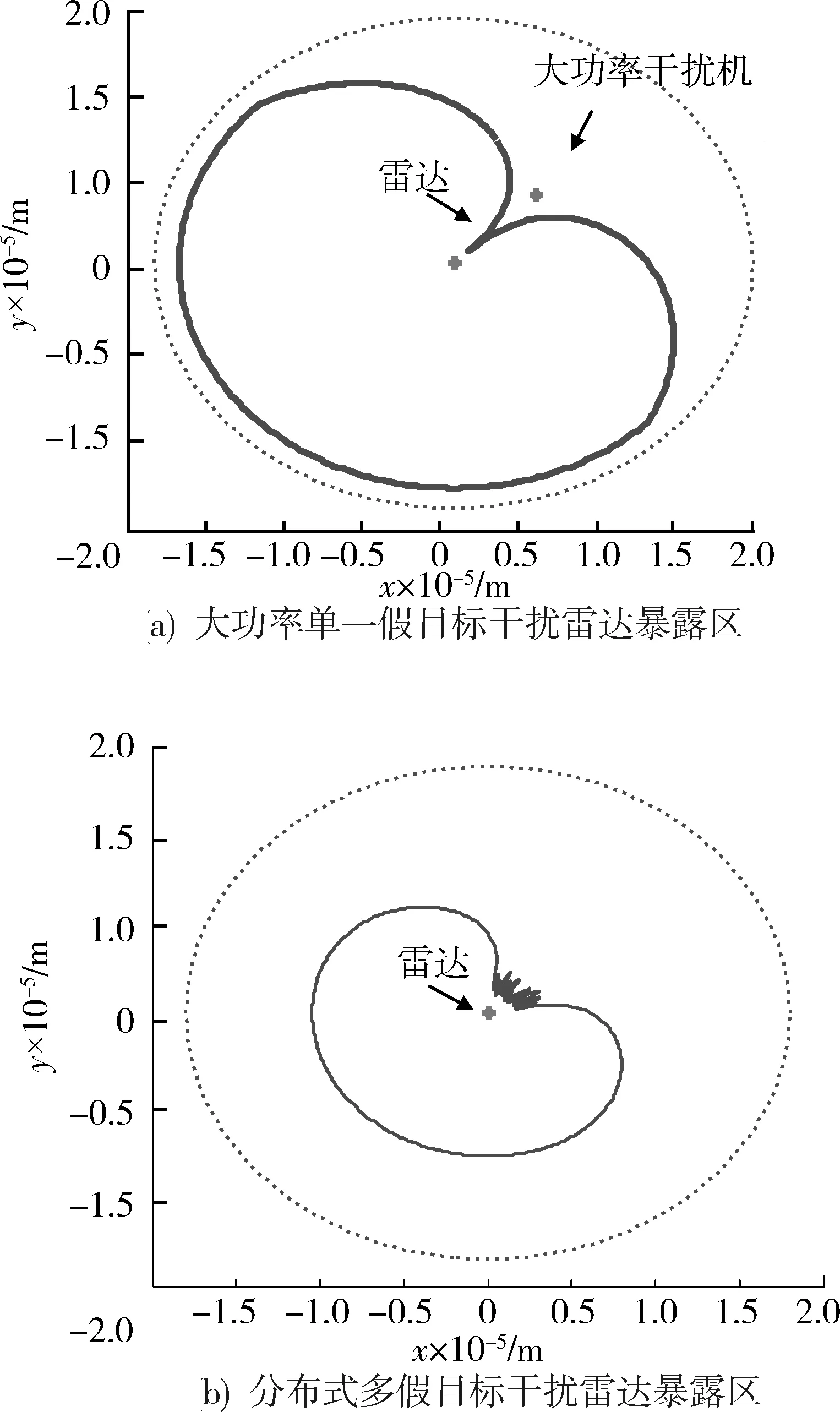
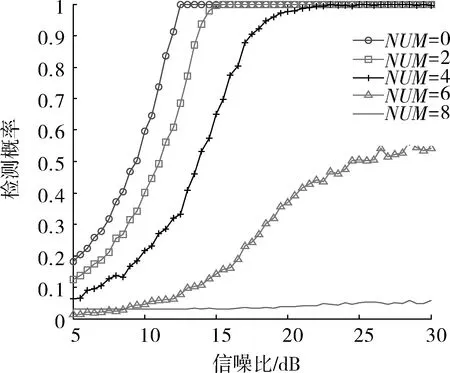
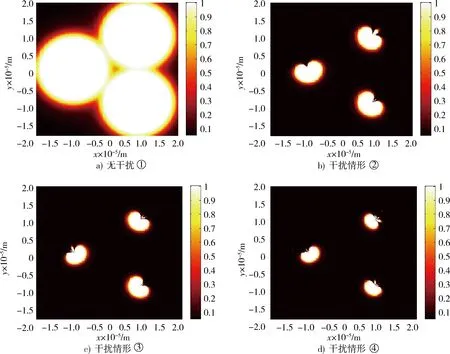
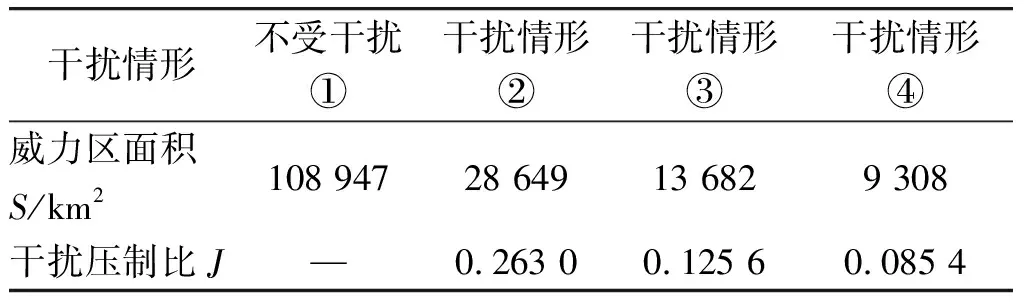
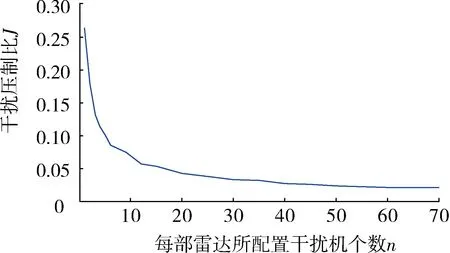
当Rf>R0时,产生置后假目标;Rf (2) 多普勒频移量 fre=f0+fd, (2) 式中:f0为雷达发射的信号频率。 则干扰机转发的信号频率为 (3) 在确定了假目标的距离延迟量和多普勒频移量之后,干扰机就可以利用DRFM技术对接收到的雷达信号进行采样、调制转发,从而产生多假目标干扰信号。 组网雷达的分布式多假目标干扰就是对雷达网中的每部雷达都进行分布式多假目标干扰,即根据分布式多假目标干扰原理和多假目标产生方法对雷达网中每部雷达都进行分布式多假目标干扰。对组网雷达进行分布式多假目标干扰时,多假目标干扰将会降低组网雷达的CFAR处理系统性能,并且造成数据融合中点迹-点迹关联和点迹-航迹关联的错误率,从而降低了组网雷达的检测性能。 为了分析多假目标干扰对组网雷达系统检测性能的影响,本文从多假目标干扰对单部雷达CFAR处理的影响出发,从而间接说明分布式多假目标干扰对组网雷达CFAR处理的影响。对目标的自动检测的CFAR方法最主要的是均值类(mean level,ML)方法和有序统计类(order statistics,OS)方法[6]。ML类单脉冲CFAR检测器结构如图1所示。 图1 ML类单脉冲CFAR检测器结构框图Fig.1 Single pulse CFAR block diagram of ML class detector 多假目标干扰是在真目标前后形成一系列假目标,这些假目标恰好落在相邻目标或假目标的CFAR参考单元里,抬高了检测门限,使雷达不能检测到该方向上干扰区域内的任何目标,从而使得真实目标的检测概率降低。 文献 [7-8]针对多假目标干扰对单部雷达CFAR处理的影响进行了详细的理论推导和分析,本文通过多假目标干扰对单部雷达CFAR处理的影响,间接说明多假目标干扰对雷达网检测性能的影响,具体的理论推导和分析不再赘述,下文将给出仿真分析。 多假目标干扰会影响CFAR处理的性能,使其对真实目标的检测概率降低,而组网雷达的检测概率是反映组网雷达检测性能的评估指标。本文将根据Alberhseim[9-10]经验公式建立分布式多假目标干扰下组网雷达检测概率计算模型。通过此模型可以求出分布式多假目标干扰下组网相控阵雷达对空间任意位置目标的检测概率,分析分布式假目标干扰对组网雷达检测概率的影响。 关于雷达检测概率Pd,虚警概率Pfa和SNRm三者之间的关系,Alberhseim建立了一个适用于非起伏目标的雷达检测概模型[4-5],并将脉冲积累个数作为一个参数集成到模型中。可表示为 lg(A+0.12AB+1.7B), (4) 雷达专家M.I.Skolnik指出:式(4)在m∈[1,8 096],Pd∈[0.1,0.9],Pfa∈[10-7,10-3]范围内的误差不大于0.2 dB。式(4)适用于非起伏目标,对于起伏目标而言,可通过查表得到目标起伏损耗Lf后加以修正。 在无干扰情况下,当积累m个脉冲时,雷达的最大探测距离为 (5) 式中:SNRm为积累m个脉冲时检测目标所需信噪比;Pt为雷达的发射功率;Gt为雷达发射天线增益;Gr为接收天线增益;λ为工作波长;D为脉冲压缩雷达的压缩系数;σ为目标有效反射截面积;Ls为雷达系统损耗;Lf为目标起伏损耗。N0=kT0BFn,其中,k为玻尔兹曼常数,T0一般取290 K,B为接收机噪声带宽,Fn为接收机噪声系数。 可将式(5)简写为 (6) 式中:Kc为一个除σ和Rmax之外的所有参数的整合因子。 雷达的最大作用距离Rmax通常为公开的参数,可定义为虚警概率为10-6,检测概率为0.5时对RCS为1 m2目标的探测距离。在已知Rmax的情况下,可以根据式(4)和式(5)可求得整合因子Kc值。可得 (7) 根据式(7)和式(4)可求得雷达对在任意距离处目标的检测概率为 (8) 根据无干扰时单部雷达检测概率公式,下面推导受分布式假目标干扰时单部雷达的检测概率公式。对单部雷达的分布式假目标干扰如图2所示。 图2 对单部雷达的分布式协同干扰示意图Fig.2 Distributed collaborative jamming against single radar 设Pji为第i(i=1,2,…,n)部干扰机的干扰功率,Rji是第i部干扰机距雷达的距离,各部干扰机均对准雷达方向,Gji为第i部干扰机天线发射增益,雷达接收到第i部干扰机发射的干扰信号功率为 (9) 设干扰信号功率远大于雷达接收机内部噪声,n部干扰机对雷达进行分布式干扰,则受假目标时雷达接收到目标回波功率与干扰信号功率之比,即信干比可表示为 (10) 式中:γji为第i部干扰机干扰极化系数;Lji为第i部干扰机的综合损耗因子;Laj为信号传播过程中的损耗因子;Gr(θi)为雷达天线在第i部干扰机方向上的增益,具体计算见文献[11-12];Br为雷达接收机的等效带宽;Bji为第i部干扰机发射的干扰信号带宽。 根据Alberhseim经验公式和式(10),可以求得在假目标条件下雷达在任意距离处的检测概率可表示为 (11) 式中:I满足如下关系: (12) 将不同目标距离R处所得SJR代入式(12),便可求出I,最后代入式(11)中便可求得分布式假目标干扰下单部雷达在任意点的检测概率Pjd。 为了衡量组网雷达在分布式假目标干扰前后的检测性能,将探测区域划分为长Δx,宽Δy,高Δz的一个个小单元,每个小单元的检测概率用其中心点的检测概率表示。那么所有的检测概率可以存储为一个大小为Lx×Ly×Lh的矩阵P。 假设组网雷达由N部雷达组成,对于目标的发现采取秩K融合规则,即当组网雷达内发现目标的雷达数超过检测门限K时,即判断为发现目标。 当K=1时,秩K法则就是“or”法则,每个小单元的检测概率可表示为 (13) 当K=N时,秩K法则就是“and”法则,每个小单元的检测概率可表示为 (14) 式中:Pdn为第n部雷达在(x,y,z)处的检测概率。 当1 (15) 由上文可知,组网雷达在某单元区域的检测概率大于一定值时,表明组网雷达在此位置可探测到目标。这些满足条件的单元区域之和构成了雷达网的可探测区域。记干扰前雷达网的可探测区域面积为SAnet,受干扰时可探测区域面积为SBnet。干扰压制比J定义 (16) 干扰压制比J直接反映了组网雷达受干扰前后探测区的变化范围,J越大压制干扰效果越好,可以作为压制干扰效果评估指标。 实验1:干扰暴露区对比 本文主要对分布式多假目标干扰下组网雷达检测性能进行研究,为了说明分布式干扰相对于传统单一大功率的优势,首先给出分布式多假目标干扰和单一大功率假目标干扰下的雷达暴露区。设一部大功率干扰机距雷达70 km,干扰机功率为1 000 W;而分布式多对一假目标干扰中共有20个干扰单元,随机分布在距雷达20 km,中心角度为π/3的扇形区域内,每个干扰单元的干扰功率为50 W,在2种干扰方式下的雷达暴露区示意图如图3所示(图中虚线表示无干扰时雷达最大可探测范围)。 图3 受假目标干扰时雷达暴露区示意图Fig.3 Radar exposition range on multi-false target jamming 由图3可知,与大功率单一干扰相比,虽然分布式假目标干扰单元功率较低,但由于干扰机可以置于离雷达更近的位置,其干扰效果较好,雷达的暴露区面积明显较小,雷达探测距离较小,且有效干扰扇面明显较大,从而说明分布式多假目标干扰是更加有效的干扰方式。 实验2:假目标干扰对雷达CFAR检测性能 实验1从雷达暴露区变化验证了分布式多假目标干扰具有更好的干扰效果。若对雷达网中每部雷达都进行分布式多假目标干扰,干扰不仅会影响雷达网的暴露区,而且会对网中雷达的CFAR处理产生影响。选取ML(meal level)中的CA(cell averaging)方法进行仿真,图4为分布式假目标干扰对单部雷达的CFAR检测性能影响。图中“NUM”表示在参考单元内假目标的数量。 图4 CA-CFAR检测性能Fig.4 CA-CFAR detection performance 由图4可以看出,在多假目标干扰存在情况下,相控阵雷达CFAR检测性能受到了影响,且假目标数目越多,检测性能下降越严重,当假目标数目大于8时,检测概率小于0.1。 若对雷达网中每部雷达都进行多假目标干扰,则同样会使雷达网的CFAR检测性能下降。 实验3:分布式假目标干扰下组网雷达检测概率计算 实验1,2从不同方面说明了分布式假目标干扰对组网雷达的干扰效果,现在根据上述所建分布式假目标干扰下组网雷达检测概率模型,对组网雷达检测概率进行仿真分析,并对干扰效果评估指标干扰压制比进行定量计算。 仿真参数设定:某组网相控阵雷达由3部相同的相控阵雷达组成,3部雷达的位置分别为(-100,80,0)km,(100,80,0)km,(0,-90,0)km。雷达发射功率为5×106W,天线增益为40 dB,接收机带宽为5.5 MHz。分布式假目标干扰系统中各干扰单元相同,各干扰单元的天线增益为10 dB,干扰功率为50 W。 设有4种干扰情形:①无干扰;②每部雷达配置2部分布式干扰机;③每部雷达配置4部分布式干扰机;④每部雷达配置8部分布式干扰机。 设雷达脉冲积累数m=1,目标的散射截面积σ=1 m2,组网雷达的融合规则采用“秩1”法则。各干扰单元与所干扰雷达距离为35 km,分布在雷达中心角度为π/3的扇形方位区域内。在上述4种干扰情形下,组网雷达在长宽各为400 km,高度为5 km的观测平面上的检测概率分布如图5所示。 图5 不同干扰情形下组网雷达的检测概率分布Fig.5 Netted radar detection probability on different conditions 图5中,区域颜色越浅说明组网雷达在该区域的检测概率越高。由图5可知,随着干扰机个数增多各部雷达的暴露区面积随之减小,暴露区的凹缝所对的方向即为分布式干扰机所在方向。仿真验证了所建模型是合理可行的。 将观测空域分为若干扰个面积为1 km2的小方格,若每个小方格中心的检测概率大于0.5则记1,在此观测空域内,得到上述4种情形的干扰压制比计算结果如表1所示。 表1 干扰压制比计算结果Table 1 Interference suppression ratio result 若对每部雷达配置数量不同的干扰机,则组网雷达的干扰压制比变化曲线如图6所示。 图6 干扰压制比变化曲Fig.6 Interference suppression ratio curve 由图6可知,随着干扰机个数增多,干扰压制比J逐渐减小并趋于稳定值,对每部雷达的干扰机配备数量大于10时,干扰效果变化不大。在实际的干扰资源调度中,对干扰资源配置有一定的指导意义。 本文重点研究了分布式多假目标干扰对雷达组网检测性能的影响。首先提出了对组网雷达的分布式多假目标干扰原理及干扰信号产生方法,然后通过分析分布式多假目标干扰对组网雷达CFAR的影响,建立了一个高精度的组网雷达检测概率计算模型,并定义了干扰压制比对干扰效果进行评估。仿真实验表明,分布式多假目标干扰对组网雷达的CFAR和检测性能具有明显影响,能够显著降低CFAR的性能和雷达网的检测概率。并通过干扰压制比计算分析为干扰资源调度提供作战辅助决策,具有较大的理论和现实意义。 参考文献: [1] 向龙,丁建江,杨大志,等.压制干扰条件下雷达组网检测概率建模与仿真[J].火力与指挥控制,2011,36(3):92-94. XIANG Long,DING Jian-jiang,YANG Da-zhi,et al. Modeling and Simulation on Detection Probability of Netted Radar In Suppression Jamming Environmen[J]. Fire Control & Command Control, 2011,36(3):92-94. [2] 刘伟,周怀军.多假目标干扰对雷达检测性能影响分析[J].现代防御技术,2009,37(4):137-142. LIU wei,ZHOU Huai-jun.Radar Detection Performance Influenced by Jamming of Multi-False Targets[J].Modern Defence Technology, 2009,37(4):137-142. [3] 杨大志,丁建江,谢超.基于分布式检测的组网探测概率模型与仿真[J].现代雷达, 2008,32(12):24-27. YANG Da-zhi,DING Jian-jiang,XIE Chao. Modeling and Simulation of Detection Probability Based on Distributed Detection in Netted Radar System[J]. Modern Radar, 2008,32(12):24-27. [4] BASSEM R M, Atef Z Elsherbeni. Radar Systems Analysis and Design Using Matlab [M]. BocaRaton: CHAPMAN & HALL/CRC, 2000. [5] MERRILL S. Radar Handbook [M].New York: McGraw-Hill, 1990. [6] 何友,关键,彭应宁,等.雷达自动检测与恒虚警处理[M].北京:清华大学出版社,1999. HE You,GUAN Jian,PENG Ying-ning,et al.Radar Automatic Detection & CFAR[M].Beijing: Tsinghua University Press,1999. [7] 施龙飞,周颖,李盾,等.LFM脉冲雷达恒虚警检测的多假目标干扰研究[J].系统工程与电子技术,2005,27(5):818-822. SHI Long-fei,ZHOU Ying,Li Dun,et al.Multi-False-Target Jamming Effects on the LFM Pulsed Radar’s CFAR Detection[J].Systems Engineering and Electronics, 2005,27(5):818-822. [8] 张振华,刘洪亮,朱国富,等.多假目标干扰对恒虚警检测效果分析[J].中国雷达,2009,11(4):9-12. ZHANG Zhen-hua,LIU Hong-liang,ZHU Guo-fu,et al. CFAR Detection Performance Influenced by Jamming of Multi-False Targets[J].China Radar,2009,11(4):9-12. [9] ALBERSHEIM W J. A Closed-Form Approximation to Robertsons′ Detection Characteristics [J].Proceedings of the IEEE,1981,69(7): 839-843. [10] TUFTS D W,CANN A J.On Albersheim’s Detection Equation[J].IEEE Transactions on Aerospaceand Electronic Systems, 1983, 19(4): 643-646. [11] 曹永辉,李侠,蔡万勇,等.分布式干扰条件下的雷达网探测威力研究[J].中国雷达,2008,12(4):14-17. CAO Yong-hui,LI Xia,CAI Wan-yong,et al.Radar Target Detection Rang Study Base on Distributed Jamming[J].China Radar, 2008,12(4):14-17. [12] 赵志超,饶彬,王涛,等.雷达网检测概率计算及性能评估[J].现代雷达,2010,32(7):7-10. ZHAO Zhi-chao,RAO Bin,WANG Tao,et al.Detection Probability Calculation and Performance Evaluation ofRadar Network[J]. Modern Radar, 2010,32(7):7-10.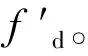
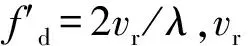
1.3 对组网雷达的分布式多假目标干扰
2 多假目标干扰对雷达网CFAR处理的影响
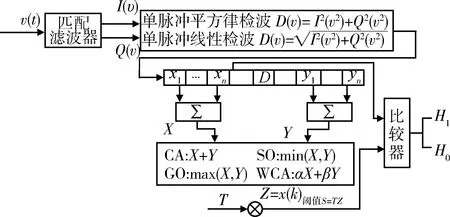
3 分布式多假目标干扰下雷达检测概率模型
3.1 无干扰时单部雷达检测概率
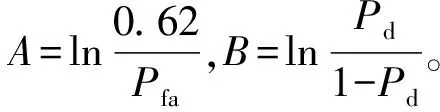
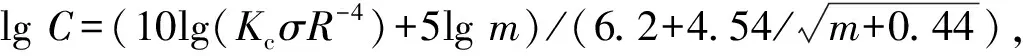
3.2 假目标干扰下单部雷达检测概率
3.3 分布式假目标干扰下组网雷达检测概率
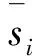
4 仿真分析
5 结束语

