气动力/推力矢量复合控制地空导弹解耦方法*

陈伟，吴晓燕

(空军工程大学 防空反导学院，陕西 西安 710051)

0 引言

为适应现代战争中快速、全方位、超低空、多目标等作战要求的特点，地空导弹必须具有更大的机动性和敏捷性，其发射方式也已经逐渐由倾斜发射向垂直发射过渡[1]。这类新型的地空导弹通常采用气动力/推力矢量复合控制，它克服了在垂直发射时，仅靠空气舵不能完成导弹姿态快速调转的不足，而且实现高速转弯，但这使导弹在初始调转段处在大攻角的飞行状态，呈现较严重的非线性和耦合特性，给控制回路的设计带来了困难，因此必须对导弹进行解耦[2]。

文献[3]对导弹的解耦方法进行了综述，主要介绍了近几年国内外应用于导弹控制系统的解耦方法；文献[4]提出了一种动力学解耦的改进直接力控制技术，仿真结果证明了基于逆动力学的直接力控制系统可以实现飞行器姿态运动和质心运动的解耦控制，并且具有较强的抗扰动能力和鲁棒性；文献[5]在BTT(bank-to-turn)导弹的纵向和横向通道分别设计了基于模型跟踪的最优控制器，满足了BTT控制的三轴解耦要求；文献[6]探讨了采用反馈-前馈控制方式，在原来的反馈控制器的基础上，利用控制指令形成直接力控制信号，仿真结果表明，解耦控制设计可行。虽然关于解耦方法研究的文献很多，但是在实际导弹控制系统设计过程中，解耦仍是一个亟待解决的问题。

本文在考虑地空导弹垂直发射实际特点的情况下,首先建立了复合控制地空导弹的数学模型，并利用动态解耦方法将非线性耦合系统转换为线性的解耦系统，然后进行了数值仿真,验证了所用方法的有效性。

1 导弹模型建立

本文的研究对象采用气动力/推力矢量复合控制系统的正常式气动布局的地空导弹，在主动段可以同时或单独选用推力矢量舵和空气舵，因为导弹气动外形采用正常式气动布局，所以导弹空气舵的气动力特性较为简单。考虑到这个特点，可以将空气舵的气动力贡献简单看成是舵偏角的线性函数。另外，若不考虑大攻角的空气动力耦合特性，还可忽略气流扭角对空气动力的影响。基于以上的考虑，下面建立导弹气动力和气动力矩的简化模型。

为使导弹在空间六自由度运动方程不过于复杂，作如下适当假设：

(1) 设计中不考虑导弹的弹性模态，视之为刚体。

(2) 假设发动机的推力为常值，推力矢量偏转提供的力只参与导弹的纵向和侧向运动。推力矢量控制(thrust vector control,TVC)执行机构建模时假设它的推力P的大小为常值，并假设只能在俯仰面(δPz)和偏航面(δPy)偏转推力矢量，并且用2种执行机构来完成这2种偏转(没有来自TVC系统的滚转控制)[7-8]。

(3) 忽略重力的影响，只考虑控制动力和推力矢量的作用，重力的影响很容易得到补偿。

(4) 由于复合控制转弯的时间短，所以认为所研究的导弹处于短周期运动，认为导弹、转动惯量和速度是常量。

(5) 导弹质心位置不变。

参考文献[9-10]的建模方法，主要在常规刚体导弹运动方程的基础上考虑推力矢量和力矩。建立的气动舵/推力矢量复合控制导弹模型如下：

(1)

(2)

(3)

(4)

(5)

(6)

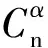
复合控制地空导弹在进行大攻角机动时，各控制通道间主要存在惯性和动力学耦合作用，在一定简化处理后，滚转通道可独立出来进行单通道控制律的设计[11]。本文主要研究俯仰/偏航2通道的解耦控制问题。

对微分方程线性化，求出俯仰/偏航通道传递函数矩阵:

(7)

通道之间耦合示意图如图1所示。系统的耦合主要是交叉惯性积耦合和导弹旋转引起的运动学耦合[12]，在传递函数矩阵中，耦合体现在反对角元素上。

图1 通道间的耦合Fig.1 Coupling between channels

2 解耦设计

考虑输入维数和输出维数相等的一个受控系统，假设其传递函数矩阵可用分式形式完全表征为

G0(s)=N(s)D-1(s),

(8)

式中：N(s)和D(s)均为p维多项式方阵。

接下来就是找到一个物理上可实现的C(s),使得闭环传递函数矩阵

GF(s)=G0(s)C(s)[I+G0(s)C(s)]-1，

(9)

是非奇异的对角线有理分式矩阵。

选取补偿器的传递函数矩阵C(s)为

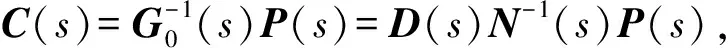
(10)

式中：

P(s)=diag(β1(s)/α1(s),…,βp(s)/αp(s))，

βi(s)和αi(s)为待定的多项式。

解耦控制原理图如图2所示。

图2 解耦控制原理图Fig.2 Theory of the decoupling method

则系统开环传递函数矩阵为

G0(s)C(s)=N(s)D-1(s)D(s)N-1(s)=

P(s)=P(s)，

(11)

从而可得输出反馈系统的闭环传递函数矩阵：

GF(s)=P(s)[I+P(s)]-1=

(12)

此时可通过选取适当的βi(s)和αi(s)来满足极点配置等其他要求。

3 仿真结果及分析

根据已有导弹数学模型，选取典型飞行高度和马赫数，得出俯仰/偏航通道传递函数矩阵模型。

根据期望极点及解耦控制需要，设计动态解耦矩阵。在俯仰方向输入正弦信号，在偏航方向输入单位阶跃信号进行对比仿真，得出图3，4的仿真结果。然后在俯仰方向上输入正弦信号，在偏航方向上输入反正弦信得出图5，6的仿真结果。

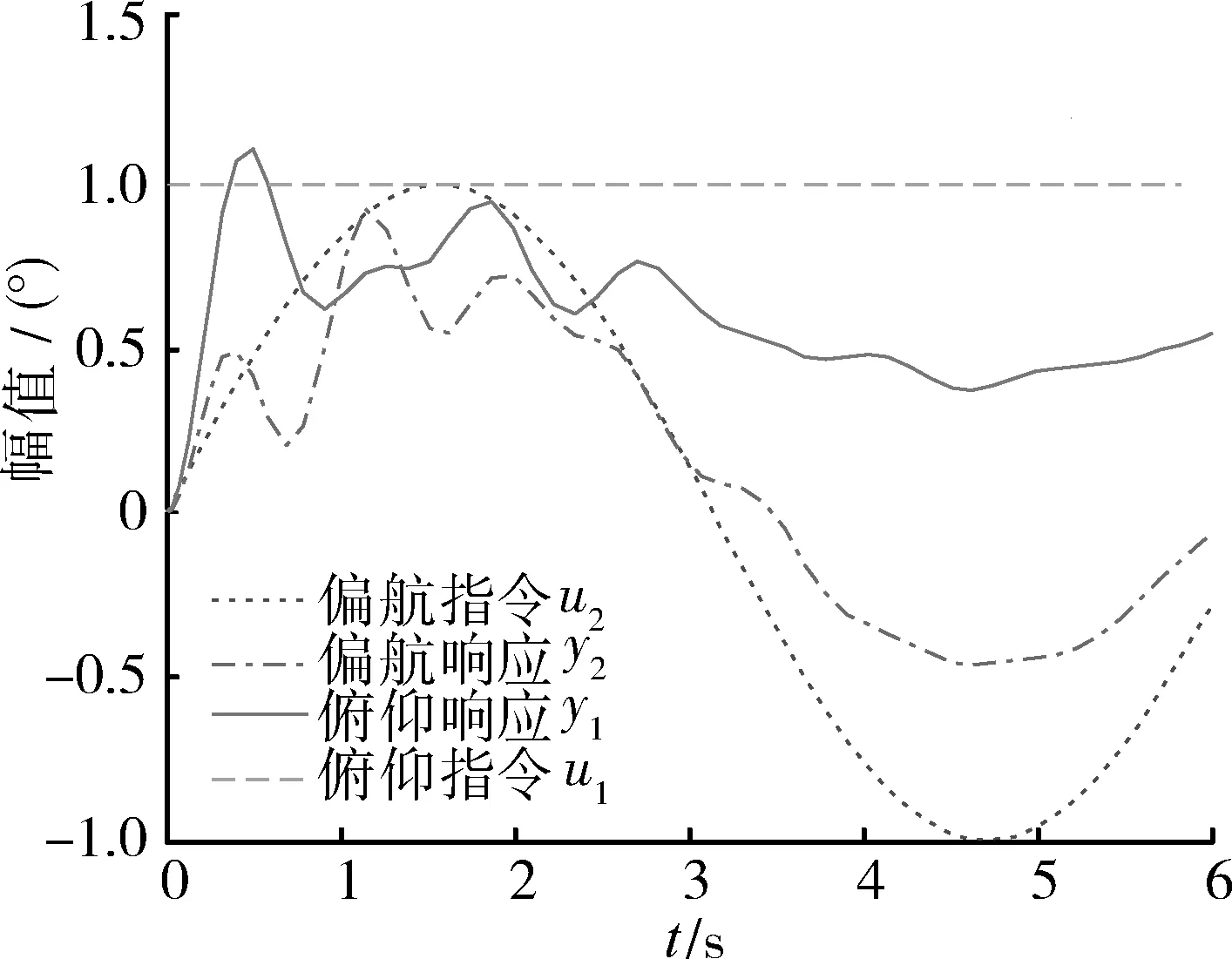
图3 解耦前系统响应Fig.3 Response before decoupling

图3～6中，u1,u2分别为俯仰和偏航指令，y1,y2分别为对应的输出响应，图3，4显示了在u1为单位阶跃信号，u2为正弦信号(幅值为1)时系统响应。图5,6显示了在u1为正弦信号，u2反正弦信号(幅值为1)时系统响应。

仿真结果显示，解耦前系统的俯仰、偏航通道之间存在严重的耦合，解耦后系统的稳定性有所加强，同时系统实现了俯仰、偏航2通道之间的解耦。

图4 解耦后系统响应Fig.4 Response after decoupling

图5 解耦前系统正弦波响应Fig.5 Sine wave response before decoupling

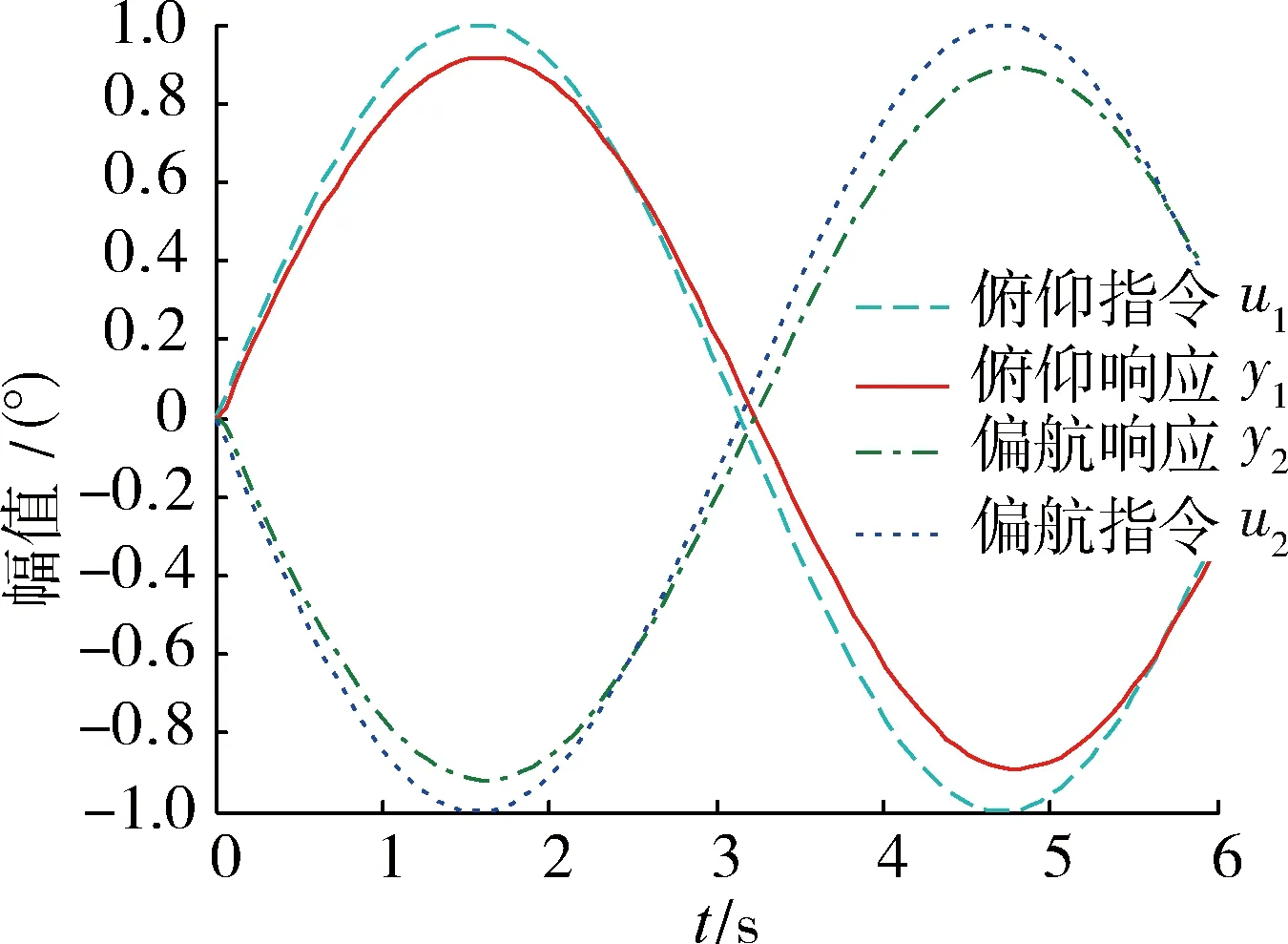
图6 解耦后系统正弦波响应Fig.6 Sine wave response after decoupling

4 结论

本文采用动态解耦方法对气动力/推力矢量复合控制地空导弹飞行动力学模型进行了解耦设计，通过仿真可以得出以下结论：

(1) 由于采用复合控制，通道间的耦合对系统性能具有较大影响，设计控制系统时必须考虑解耦问题。

(2) 本文的解耦设计满足了系统通道间分离控制的目的，下一步就是设计控制器，以匹配原有的常规控制。

(3) 本文的解耦方法是常规的解耦方法，还可以用自适应解耦控制方法、鲁棒控制来对系统进行解耦。

参考文献：

[1] 敖百强,李君龙,林维菘.战术导弹垂直发射控制的输出解耦变结构方法研究[J]. 系统工程与电子技术，2003, 25(7):829-833.

AO Bai-qiang, LI Jun-long, LIN Wei-song. Variable-Structure Control of Vertical Launching Missile Based on Output Decoupling Method[J].Systems Engineering and Electronics,2003, 25(7):829-833.

[2] 王永寿.导弹的推力矢量控制技术[J].飞航导弹，2005(1):54-60.

WANG Yong-shou. Thrust Vector Control Technology for Missiles[J].Aerodynamic Missile Journal, 2005(1):54-60.

[3] 贾杰，刘连章，曹琦.导弹解耦控制方法综述[J].航空兵器,2010(3):18-21.

JIA Jie, LIU Lian-zhang, CAO Qi. Survey on Decoupling Control Methods for Missile[J]. Aero Weaponry,2010(3):18-21.

[4] 徐聘,刘永才,强文义,等.动力学解耦的改进直接力控制[J].航空学报，2008, 29(1):15-19.

XU Cheng, LIU Yong-cai, QIANG Wen-yi, et al. Dynamics Decoupled Direct Force Control Technology. Acta Aeronautica et Astronautica Sinica, 2008, 29(1):15-19.

[5] 张平,黄雅.导弹动力学建模与BTT解耦控制[J].系统仿真学报,2006, 18(S2):773-776.

ZHANG Ping, HUANG Ya. Missile's Dynamical Modeling and BTT Decoupling Control[J]. Journal of System Simulation,2006, 18(S2):773-776.

[6] 李友年,王海波.直接力/气动力解耦控制方法[J].航空兵器,2004(3):24-25.

LI You-nian, WANG Hai-bo. Decoupling Method of Earth-to-Air Missile Using Lateral Thrust/Aerodynamic Compound Control [J]. Aero Weapornty，2004(3):24-25.

[7] 郑勇斌,林丽.采用摆动喷管推力矢量控制弹性数学模型建立[J].现代防御技术，2007, 35(1):41-44.

ZHENG Yong-bin，LIN Li. Mathematical Model of Elasticity Missiles with Swing Nozzle Thrust Vector Control [J].Modern Defence Technology, 2007, 35(1):41-44.

[8] 赵红超,王亭,顾文锦，等.弹道导弹的推力矢量控制系统设计[J].飞行力学，2007, 25(4): 44-47.

ZHAO Hong-chao, WANG Ting, GU Wen-jin, et al. Design of Thrust Vector Control System for a Ballistic Missile[J].Flight Dynamics, 2007, 25(4): 44-47.

[9] 胡孟权.推力矢量飞机非线性飞行控制律设计研究[D].西安：西北工业大学，2002:15-21.

HU Meng-quan. Research on Nonlinear Flight Control Law Design of Aircraft with Vectoring Thrust [D].Xi’an:Northwestern Polytechnical University，2002:15-21.

[10] 雷虎明.导弹制导与控制原理[M].北京：国防工业出版社,2006:17-66.

LEI Hu-min. Theory of Guidance and Control for Missile [M]. Beijing: National Defense Industry Press, 2006:17-66.

[11] 侯满义,解增辉,范惠林.复合控制空空导弹大机动控制律设计与仿真[J].弹道学报，2011, 23(4):22-26.

HOU Man-yi, XIE Zeng-hui, FAN Hui-lin. Control Law Design and Simulation for High Maneuvering Air-to-Air Missile With Compound Control [J]. Journal of Ballistics，2011, 23(4):22-26.

[12] 解增辉,刘占辰,李锐.直接力/气动力复合控制导弹通道耦合特性分析及其解耦控制[J].光电与控制，2009, 16(1):42-45.

XIE Zeng-hui, LIU Zhan-chen, LI Rui. Channel Coupling Analysis and Decoupling Control for Missile with Lateral Thrust/Aerodynamic Compound Control [J]. Electronic Optics & Control，2009，16(1):42-45.