不同制导律下天线罩误差对导弹性能的影响*

宗睿，孙宝彩,2，林德福，崔晓曦，范世鹏

(1.北京理工大学 宇航学院，北京 100081； 2.空军装备研究院 总体论证研究所，北京 100076； 3.中国兵器工业导航与控制技术研究所，北京 100089)

0 引言

反辐射导弹通过雷达导引头中的天线接收目标发射的电磁波，从而确定目标位置进行制导，而天线罩作为雷达导引头的一种常用装置，起到保护天线、防止气流扰动以及减小阻力的作用。由于天线罩形状和材质的原因，目标发射信号穿过天线罩时会发生折射，造成视线角误差，从而影响导弹制导控制系统的稳定性和制导精度[1-5]。

针对天线罩误差对制导控制系统带来的影响，Nesline和Zarchan[6]率先提出了天线罩误差寄生回路的稳定性问题，Susuma Miwa[7]讨论了三阶和五阶制导模型下天线罩误差对制导系统稳定性以及制导精度的影响，并进行了对比研究，同时分析了不同参数变化对脱靶量的影响。王志伟[8]等人采用无量纲化方法，研究了天线罩误差存在的情况下不同噪声源对脱靶量的影响。

本文从制导律出发，建立了比例导引和速度追踪制导律下的天线罩误差寄生回路模型及制导回路模型，采用伴随法和无量纲方法，分别分析了2种制导律下天线罩寄生回路的稳定性以及不同噪声源下的无量纲脱靶量，并进行了相关的对比研究，为反辐射导弹的制导控制系统设计提供理论依据。

1 天线罩误差模型

当目标发射的电磁波传输通过天线罩时，将发生弯曲或折射，从而造成错误的目标位置指示。 图1给出了天线罩影响下导弹与目标之间的几何关系。其中，qs为导引头指向角，qt为真实弹目视线角，q*为天线罩折射造成的虚假弹目视线角，ϑ为弹体姿态角，φr为导引头框架角，ε为导引头指向与真实弹目视线间的误差角，ε*为天线罩误差造成的虚假弹目视线与导引头指向的夹角。

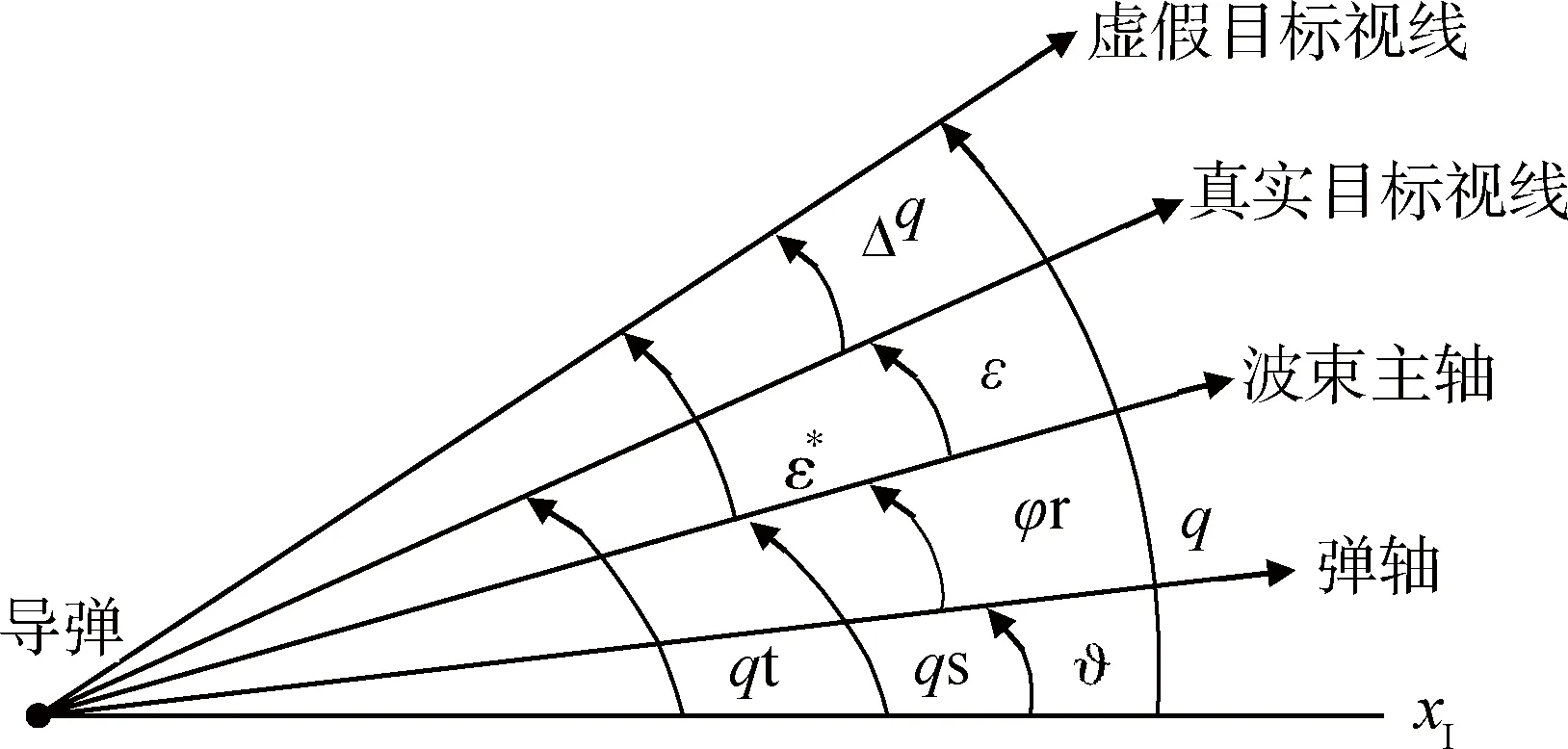
图1 天线罩影响下导弹与目标的几何关系图Fig.1 Geometrical relationship between missile and target under radome

真实弹目视线与虚假弹目视线间的夹角Δq称为天线罩瞄准误差，且与框架角φr成函数关系，即

Δq=f(φr)，

(1)

其曲线斜率称为天线罩误差斜率，定义为R。

由图1可得导引头测得的视线角q*的表达式为

q*=qt+(qs-ϑ)R.

(2)

由于导引头在稳定跟踪过程中跟踪误差角很小，可令qs≈qt，且雷达导引头天线罩误差斜率R≪1，因此可推导出：

q*≈qt+(qt-ϑ)R=qt(1+R)-ϑR≈qt-ϑR.

(3)

2 天线罩寄生回路稳定性对比

比例导引和速度追踪是目前工程上应用较为广泛的2类制导律。比例导引制导律[9]是指导弹在攻击目标的导引过程中，导弹的速度矢量转动角速度与弹目视线的转动角速度成比例的一种导引律，采用的是过载驾驶仪；而速度追踪制导律是指导弹在攻击目标的导引过程中，力图使导弹的速度矢量始终对准目标的一种导引方法，即要求导弹速度矢量与弹目视线间的偏差角为0[10]，使用的是速度矢量驾驶仪。2种制导律形式和意义不同，不能直接进行比较。本文根据工程实际，将比例导引使用的过载驾驶仪保持不变，而将速度追踪制导律中的弹道倾角进行外部反馈，构造了一种具有可比性的速度矢量驾驶仪，如图2所示。

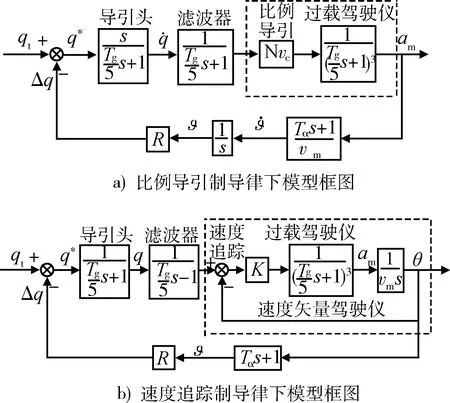
图2 2种制导律下天线罩寄生回路模型Fig.2 Parasitic loop model under two guidance laws

当弹目相对距离较远时，制导回路的稳定性主要由天线罩寄生回路的稳定性决定。由式(3)可以分别建立比例导引律和速度追踪律下的天线罩寄生回路模型，如图2所示。

其中N为导航比，vc为弹目相对速度，vm为导弹飞行速度，R为天线罩误差斜率，Tg为制导系统时间常数，Tα为攻角滞后时间常数，K为速度矢量驾驶仪的开环增益。

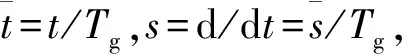
根据图3所示等效寄生回路模型，可采用数值计算方法得到寄生回路的临界稳定曲线，如图4所示。为了保证在速度追踪律下速度矢量驾驶仪良好的动态和跟踪性能，参数k取0.7，0.9，1.1三组值，k越大，速度矢量驾驶仪越快，但均慢于过载驾驶仪。

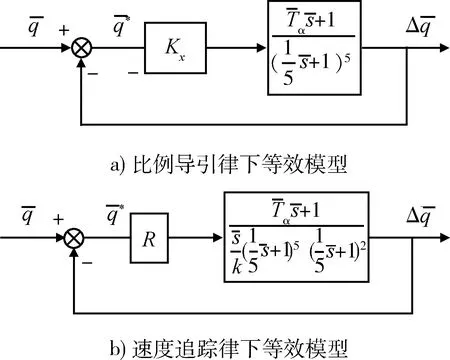
图3 2种制导律下等效天线罩寄生回路模型Fig.3 Equivalent parasitic loop model under two guidance laws

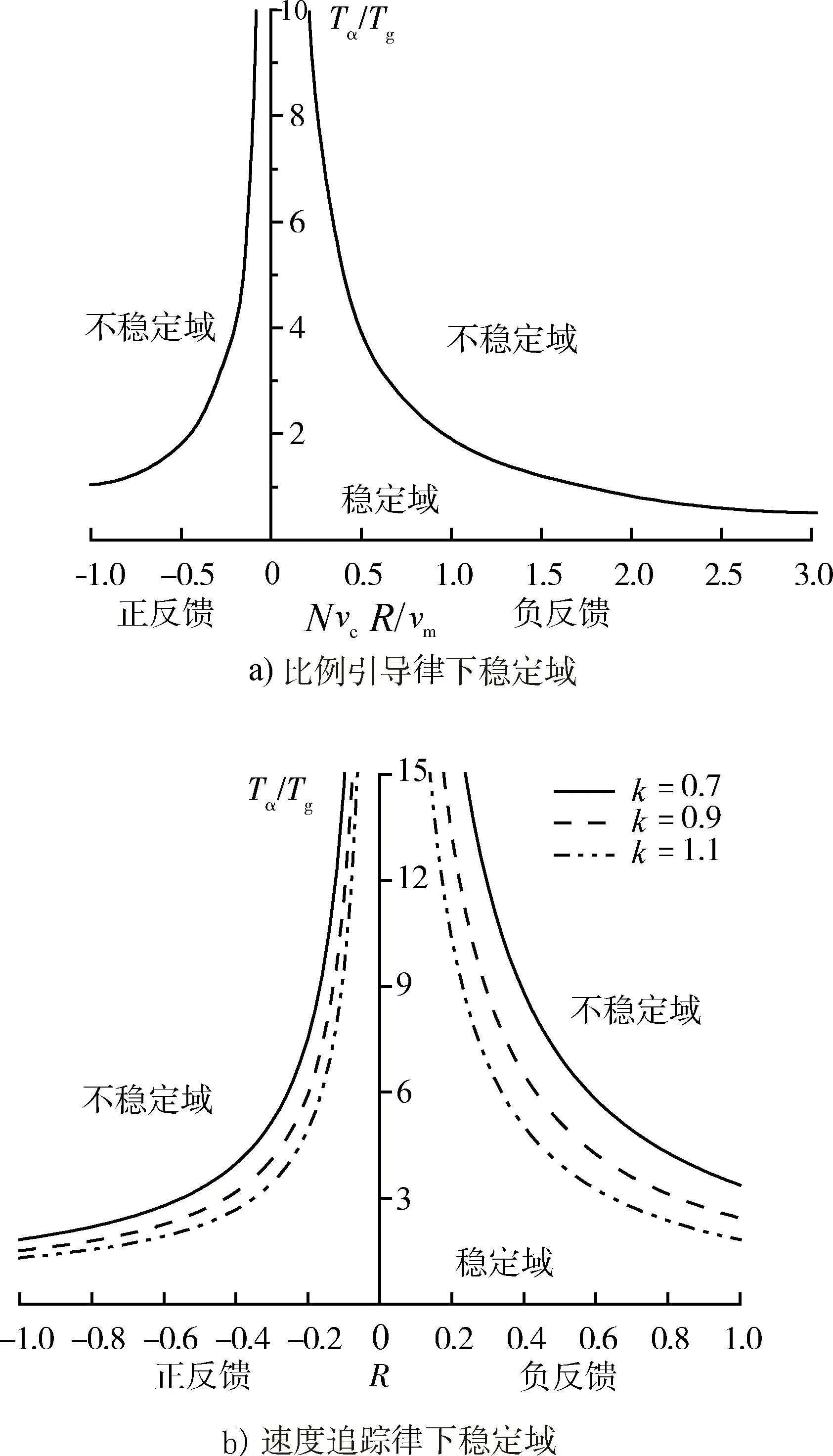
图4 2种制导律下寄生回路稳定域Fig.4 Stable region of parasitic loop under two guidance laws

由图4可知，在比例导引制导律下，寄生回路为负反馈(R>0)时的稳定域要比正反馈(R<0)时的稳定域大，且当NvcR/vm越小，即导航比N、弹目相对速度与导弹飞行速度的比值vc/vm、天线罩误差斜率R越小，寄生回路的稳定域就越大，同时攻角滞后时间常数与制导系统时间常数的比值Tα/Tg越小，寄生回路的稳定域越大。

在速度追踪制导律下，寄生回路为负反馈(R>0)时的稳定域要比正反馈(R<0)时的稳定域大，且天线罩误差斜率R越小，Tα/Tg越小，寄生回路的稳定域越大。随着系数k的增大，寄生回路的稳定域减小。

图5为比例导引和速度追踪分别选取各自典型条件下的寄生回路稳定域对比图。

图5中曲线下方为稳定域，上方为不稳定域。由图可以看出，速度追踪律对应的寄生回路稳定域要大于比例导引律对应的寄生回路稳定域，即比例导引对天线罩误差斜率R的敏感程度要大于速度追踪。

3 不同噪声下脱靶量对比

本文引入2类典型噪声源，分别为雷达导引头噪声和目标随机机动。其中雷达导引头噪声又分为闪烁噪声和接收机热噪声。同时将这2类噪声源均假设为白噪声。

(1) 闪烁噪声

闪烁噪声主要是由于震动、目标机动、目标反射波滞后、气流影响或者机载武器载机的振动、舰载武器舰只的起伏波动造成的虚假目标移动信息，它可以看成是目标的视在移动，是一种低频噪声。其功率谱密度由ΦGL来表示。

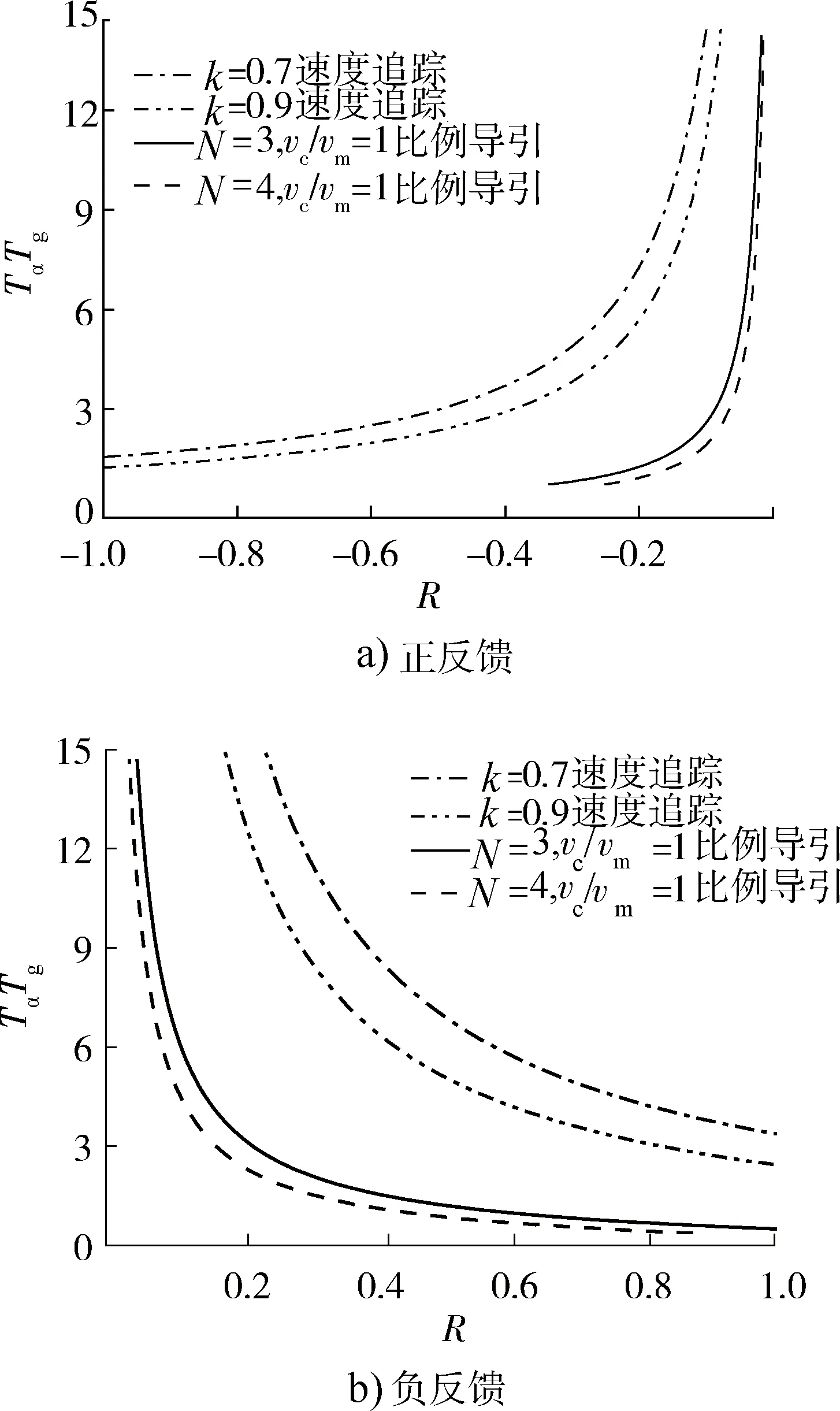
图5 2种制导律寄生回路稳定域对比Fig.5 Comparison of the parasitic loop stable region between two guidance laws

(2) 接收机热噪声

接收机热噪声是在雷达导引头接收机中产生的与距离相关的热噪声，这种噪声与导弹和目标之间的距离成正比。其功率谱密度由ΦRN来表示。

(3) 目标随机机动

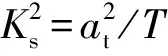
引入噪声源的制导回路模型由图6所示。

其中，若选取比例导引制导律，则天线罩寄生回路的传递函数为

(4)

若选取速度追踪制导律，则天线罩寄生回路的传递函数取

(5)

对图6所示的制导回路模型进行时间尺度无量纲化处理，可分别得到比例导引和速度追踪下的制导回路伴随系统模型[12]，如图7所示。

其中，若选取比例导引制导律，则选取

(6)

若选取速度追踪制导律，则选取

(7)

3.1 闪烁噪声对制导精度的影响

在闪烁噪声的影响下，选取无量纲制导时间T/Tg=10 s，研究比例导引和速度追踪下的脱靶量。

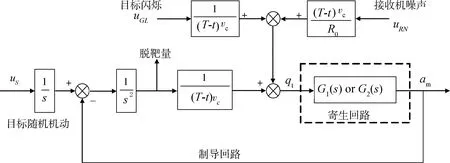
图6 不同噪声源下的制导回路模型Fig.6 Guidance loop model under different noise sources

由图8可以看出，在寄生回路稳定的条件下，使用比例导引律的脱靶量明显大于使用速度追踪律的脱靶量。对于2种制导律来说，当R<0时，R的绝对值越大，Tα/Tg越大，则无量纲脱靶量越大；当R>0时，R越大，无量纲脱靶量越小，而Tα/Tg对无量纲脱靶量的影响很小。对于比例导引律，比例系数N越大、速度比vc/vm越大，则无量纲脱靶量越大；对于速度追踪律，系数k越大，则无量纲脱靶量越大；而速度比vc/vm越大，无量纲脱靶量反而越小。

3.2 接收机热噪声对制导精度的影响

在接收机热噪声的影响下，选取无量纲制导时间T/Tg=10 s，研究比例导引和速度追踪下的脱靶量。

由图9可以看出，在寄生回路稳定的条件下，对于2种制导律来说，当R<0时，R的绝对值越大，Tα/Tg越大，则无量纲脱靶量越大，且比例导引律的脱靶量明显大于速度追踪律的脱靶量；当R>0时，R越大，无量纲脱靶量反而越小，而Tα/Tg对无量纲脱靶量的影响很小，且比例导引律的脱靶量略大于速度追踪律的脱靶量。对于比例导引律，比例系数N越大，速度比vc/vm越大，则无量纲脱靶量越大；对于速度追踪律，R<0时，系数k越大，则无量纲脱靶量越大，而R>0时，系数k越大，无量纲脱靶量反而越小；同时速度比vc/vm越大，无量纲脱靶量也越小。

3.3 目标随机机动对制导精度的影响

在目标随机机动的影响下，选取无量纲制导时间T/Tg=10 s，研究比例导引和速度追踪下的脱靶量。

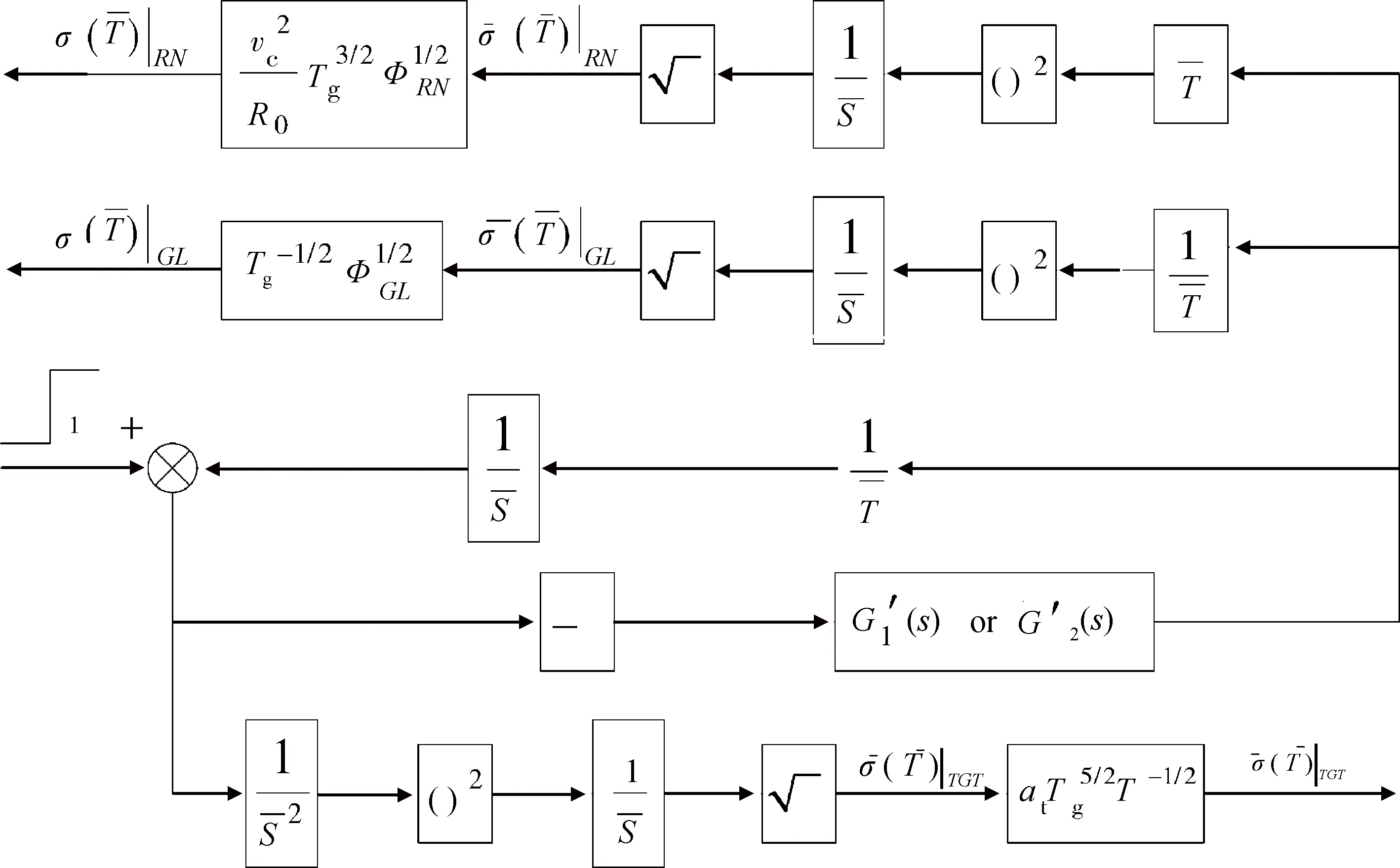
图7 无量纲化制导回路伴随系统模型Fig.7 Dimensionless adjoint system model of guidance loop

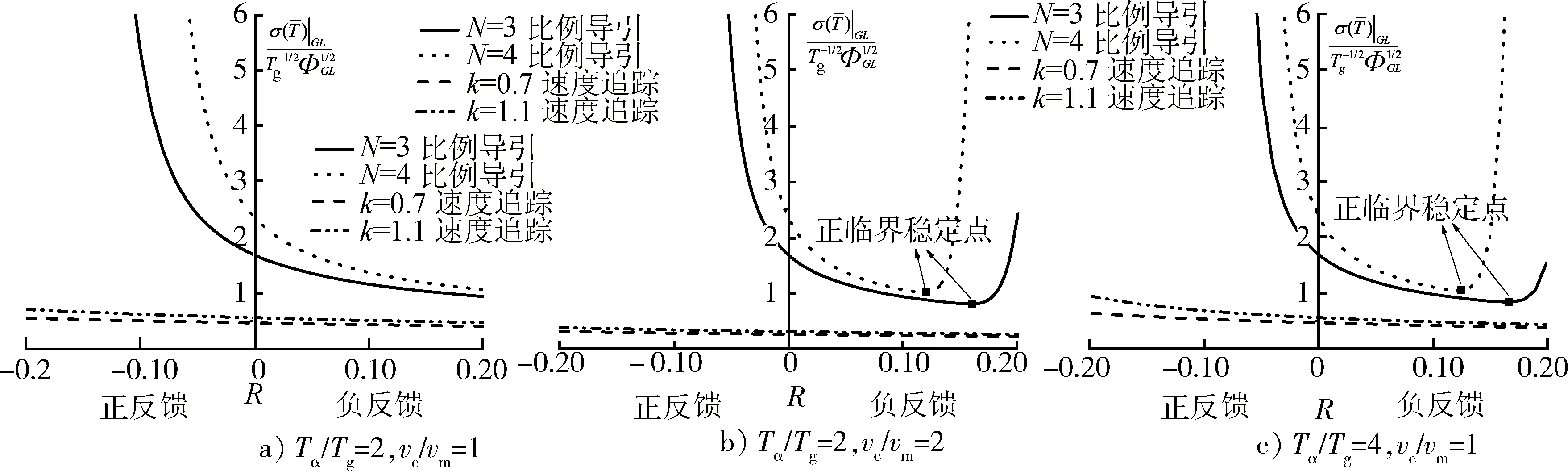
图8 闪烁噪声引起的无量纲脱靶量Fig.8 Dimensionless miss distance by glint noise

由图10可以看出，在寄生回路稳定的条件下，使用比例导引律的脱靶量明显小于使用速度追踪律的脱靶量。对于2种制导律来说，当R<0时，R的绝对值越大，则无量纲脱靶量越小，当R>0时，R的绝对值越大，无量纲脱靶量越大，而Tα/Tg对无量纲脱靶量的影响较小。对于比例导引律，比例系数N越大，速度比vc/vm越小，则无量纲脱靶量越小；对于速度追踪律，系数k越大，无量纲脱靶量越小；而当速度比vc/vm越大，无量纲脱靶也越大。

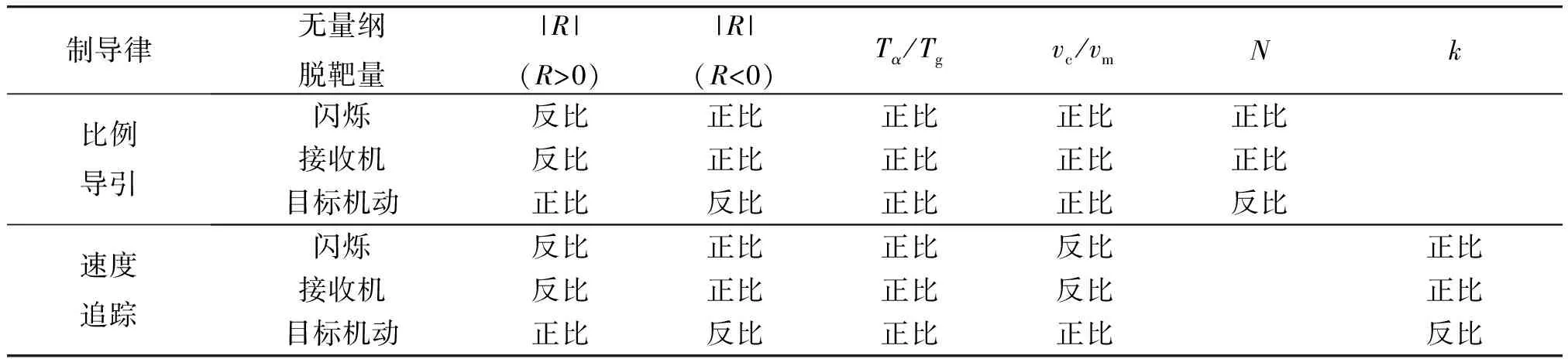
综上，表1总结了不同参数与不同噪声源下无量纲脱靶量之间的正反比关系。

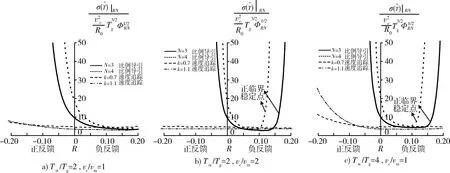
图9 接收机热噪声引起的无量纲脱靶量Fig.9 Dimensionless miss distance by received noise

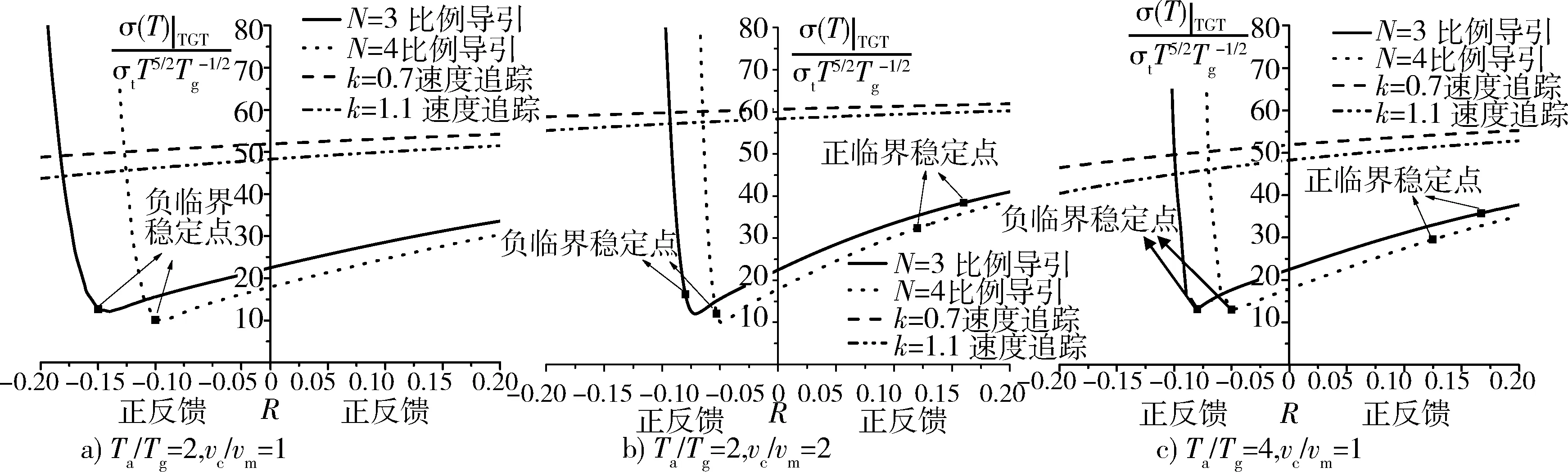
图10 目标随机机动引起的无量纲脱靶量Fig.10 Dimensionless miss distance by target random maneuvering

表1 不同参数与无量纲脱靶量之间的正反比关系

Table 1 Proportional and inverse relationship between different parameters and dimensionless miss distance

制导律无量纲脱靶量|R|(R>0)|R|(R<0)Tα/Tgvc/vmNk比例导引闪烁反比正比正比正比正比接收机反比正比正比正比正比目标机动正比反比正比正比反比速度追踪闪烁反比正比正比反比正比接收机反比正比正比反比正比目标机动正比反比正比正比反比

4 结束语

本文采用伴随法和无量纲方法，分别分析了比例导引和速度追踪2种制导律下天线罩寄生回路的稳定性和无量纲脱靶量，并通过仿真进行了对比研究。

仿真结果表明，在天线罩误差的影响下，速度追踪律对应的寄生回路稳定域要大于比例导引律；同时在天线罩寄生回路稳定的前提下，制导系统引入雷达导引头噪声时，比例导引的无量纲脱靶量要大于速度追踪，在目标随机机动的情况下，比例导引的无量纲脱靶量要小于速度追踪。天线罩误差斜率、攻角滞后时间常数与制导系统时间常数的比值、弹目相对速度与导弹飞行速度的比值等参数的变化以及制导律的选取均会对天线罩寄生回路稳定性和不同噪声源下的无量纲脱靶量产生影响，因此在进行反辐射导弹制导控制系统设计时，需要考虑上述因素并进行折中设计。

参考文献：

[1] Peter H Zipfel. Modeling and Simulation of Aerospace Vehicle Dynamics[M]. Gainesville, Florida: American Institute of Aeronautics and Astronautics, 2000.

[2] 齐宝华, 张霖. 天线罩影响下导弹制导系统稳定性分析[J]. 清华大学学报, 1998, 38(9): 102-106.

QI Bao-hua, ZHANG Lin. Stability Analysis of Missile Guidance System with Radome Effects[J]. Journal of Tsinghua University, 1998, 38(9): 102-106.

[3] TRAVERS P. Design Equations for Pro-portional Navigation with Parasitic Feed-Back[C]∥American Control Conference,Seattle, 1986：1112-1123.

[4] ZARCHAN P, GRATT H. Adaptive Radome Compensation Using Dither[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(1): 51-57.

[5] PINI G, JEREMY K. Improving Missile Guidance Performance by in-Flight Two-Step Nonlinear Estimation of Radome Aberration[J]. IEEE Transactions on Control System Technology, 2004, 12(4):532-541.

[6] WILLIAM NESLINE F, ZARCHAN P. Radome Induced Miss Distance in Aerodynamically Controlled Homing Missiles[C]∥AIAA Guidance & Control Conference, Seattle， 1984： 99-115.

[7] Susumu Miwa. Radome Effect on the Miss Distance of a Radar Homing Missile[J]. Electronics and Communications in Japan, 1998, 83(7): 14-22.

[8] 王志伟, 李保平, 林德福, 等. 天线罩误差对无线电制导导弹性能的影响[J]. 弹箭与制导学报, 2008, 28(2): 53-56.

WANG Zhi-wei, LI Bao-ping, LIN De-fu, et al. The Effect of Radome Aberration on RF Guided Missile[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2008, 28(2): 53-56.

[9] MEHRANDEZH M. Robotic Interception of Moving Objects Using an Augmented Ideal Proportional Navigation Guidance Technique[J]. IEEE Transactions on Systems,Man and Cybernetics, 2000, 30(3): 231-244.

[10] 宋锦武, 夏群力, 徐劲祥. 速度追踪制导律制导回路建模及解析分析[J]. 兵工学报, 2008, 29(3):323-326.

SONG Jin-wu, XIA Qun-li, XU Jin-xiang. Modeling and Analysis of Guidance Loop with Velocity Pursuit Guidance Law[J]. Acta Armamentarii, 2008, 29(3):323-326.

[11] GARNELL P. Guidance Weapon Control Systems[M]. 2nd Revision by Prof. QI Zai-kang，XIA Qun-li. Beijing: Beijing Institute of Technology, 2003.

[12] ZARCHAN P. Tactical and Strategic Missile Guidance[M]. Lexiongton,Massachusetts: American Institute of Aeronautics and Astronautics, 2002.