基于双模预测的大气层内拦截弹中制导律研究*

李爽，江涌，李君龙，张奕群

(1.北京电子工程总体研究所，北京 100854； 2.中国航天科工集团 防御技术研究院，北京 100854)

0 引言

大气层内目标拦截弹末制导侧窗探测技术的采用对中末制导交班提出特殊要求。除此之外，中制导过程还要受到气动热、过载、动压、迎角等对状态和输入的约束。针对中末制导交班约束，文献[1-2]分别研究了基于虚拟目标的LQR(linear quadratic regulator)中制导律和虚拟目标的位置参数设置方法。拦截弹在该导引律作用下可以在中制导末端满足侧窗视场和交班高度等要求，为中末制导交班提供良好的条件。但是，LQR不能处理控制和状态约束，并且在处理环境的多变性方面缺少预见性。

模型预测控制(model predictive control,MPC)凭借其特有的滚动时域优化和多步预测措施，在保证系统的鲁棒性和稳定方面显示着巨大的优越性[3]。尤其是其显式处理状态和输入约束的功能使其在有约束系统领域受到推崇，目前已经应用到航天飞机、卫星姿态控制等领域[4]。文献[5-7]提出了适用于各类采用惯性弹道与非惯性弹道的再入飞行器的预测制导律的设计方法，但此类方法只针对确定目标，主要用于再入阶段的系统不确定性。文献[8]通过迭代优化，不断修正控制模型参数，保证飞行器顺利进入末制导。然而，MPC的滚动优化所要求的繁重的计算量阻碍其在快速取样系统中的推广。针对此问题，文献[9]提出牛顿-辛普森模型预测控制(Newton-Raphson MPC,NRMPC)，通过将部分在线计算转嫁到离线过程，大大降低了在线计算量。文献[10-12]又对NRMPC进行了改进，使MPC在快速取样系统中的广泛应用成为可能。

基于上述研究成果，本文先设计出针对虚拟目标的常系数次最优制导律，再通过对控制信号引入有限维扰动，建立双模闭环反馈控制系统，再通过模型扩展和在线优化问题几何意义的分析，引入牛顿-辛普森算法完成在线计算，以提高计算效率。

1 弹目运动学模型

针对大气层内目标拦截弹的侧窗探测对中末制导交班的特殊要求，文献[1-2]提出一种虚拟目标的设置方法，如图1所示，虚拟目标T′相对于实际目标T静止，拦截弹以虚拟目标位置和速度所决定的终端弹道角σh和终端视线角qh与T′交会时，实际目标正好落在拦截弹导引头的给定视场位置，且相对于实际目标的瞬时脱靶量为0。这一交会过程构成中制导过程，其弹道可以很好地满足中末制导交班的特殊要求。

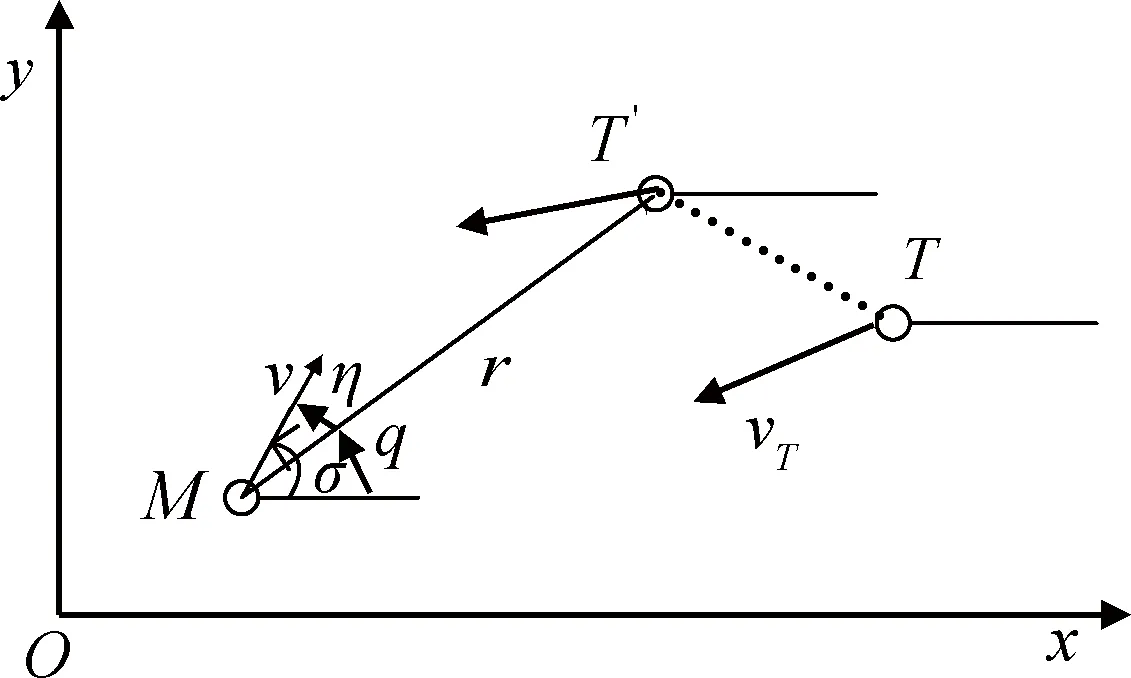
图1 拦截弹与虚实目标位置示意图Fig.1 Sketch map of interceptor，virtual and actual targets position

由图1得拦截弹与虚拟目标的相对运动方程

(1)

(2)

η=σ-q，

(3)

ηT′=π-σT′-q.

(4)

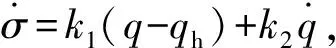
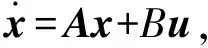
(5)

式中：

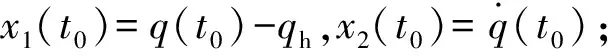
x1(th)=0，x2(th)=0,th为交点时间。

假设拦截弹在中制导过程中的热约束、过载和动压等约束适当处理后，可以简化成下面的一般形式

Hx≤h.

(6)

2 双模预测制导律

为了保证闭环拦截系统的稳定性和自适应性，应该采用时变反馈控制律制导。又由于系统存在严格的控制和状态约束，因此采用能显式处理多变量约束的模型预测控制方法。若直接对非线性系统(5)提出预测控制，在线计算量太大，难以在快速取样系统中实现。为了保证系统的可行性和稳定性，并减小在线计算量，这里提出双模预测中制导律，整个控制策略如图2所示[9]。

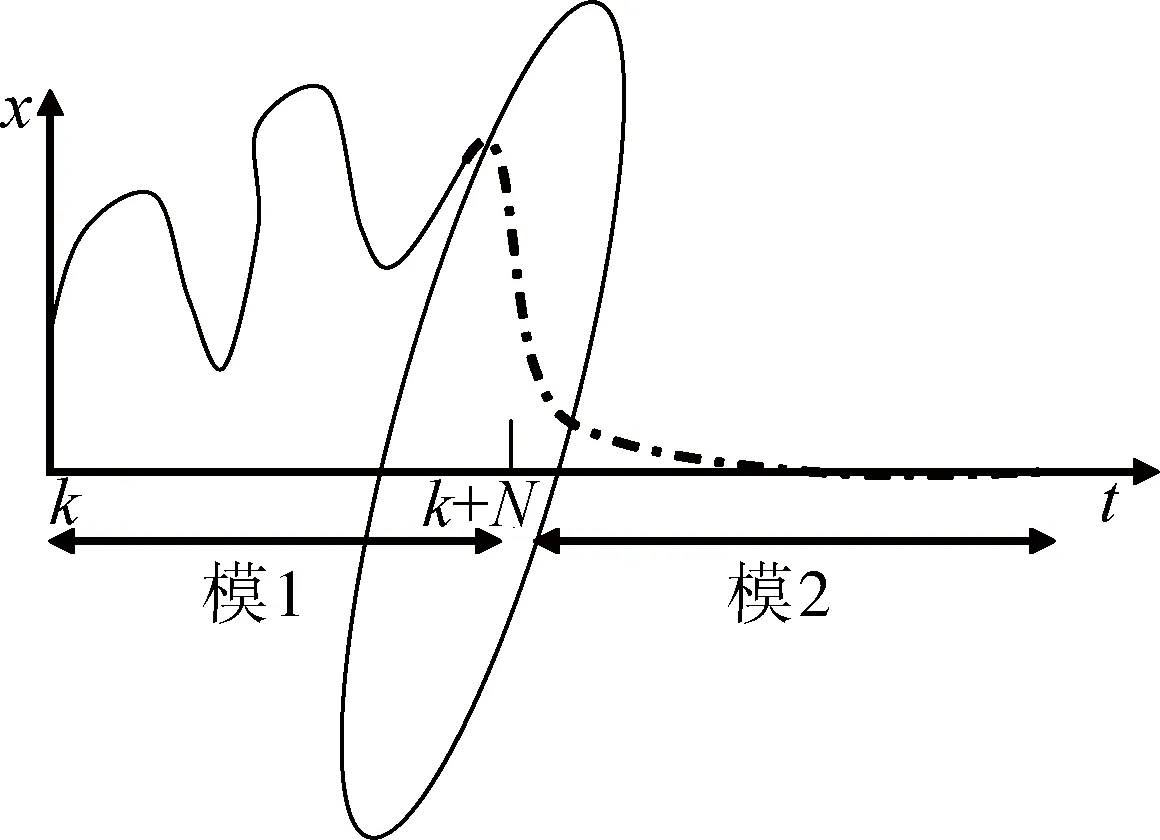
图2 双模预测控制模型Fig.2 Model of dual mode predictive control

反馈控制系统的前N步构成模1，采用约束条件下的优化自由控制律，通过这N步的控制，使N+1时刻的状态进入x的集合εx内；N步之后构成模2，采用常系数反馈控制，即

模1u=Kxk+c,Hx≤h,k=1,2，…,N,

(7)

模2u=Kxk,xk∈εx,k=1,2，…,N.

(8)

这里的εx定义为模2中的常系数反馈控制律下的可行不变集，即εx内的所有状态均满足约束(可行性)，且只要k时刻xk∈εx，则xk+1∈εx成立(不变性)。反馈控制律拟采用下面的次最优制导律。

2.1 次最优制导律设计方法

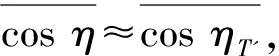
式中:p=v/vt。

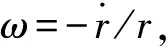
式(5)中的参数矩阵变为

取二次性能指标函数

(9)

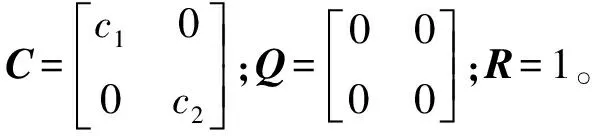
应用最优控制理论，可得系统的最优制导律

u=-R-1BTPx.

(10)

解Riccati方程

P(t)B(t)R-1BT(t)P(t)-Q(t)，

(11)

P(t)的终端条件P(tf)=C。

式(11)可以分解为下面2个方程

(12)

(13)

W(t)和Y(t)的终端条件为

W(tf)=I,

Y(tf)=C.

Riccati矩阵微分方程的解为

P(t)=Y(t)W-1(t).

(14)

u=k1x1+k2x2，

(15)

式中：k1和k2的值随c1和c2的取值而不同。

根据对制导过程中可用过载和导引头视线偏差角的要求，一般情况下，k1可取值0.05～0.2，k2可取值2～6，k1的值越大，交接段导引头视线偏差角越小，但是如果k1过大，则会增大中制导末端的预测脱靶量。k2的取值规律及作用类似于比例导引。

2.2 基于吊装模型的双模预测制导

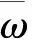
xk+1=Adxk+Bduk，
Ad=TA+I,Bd=TB，
uk=Kxk，

(16)

式中：T为采样时间。

终端状态约束xtf为0的情况下，式(9)中的指标函数简化为

(17)

式中：xk+i，uk+i表示预测状态和输入向量。

为了保证过程约束得到满足，如图2所示，在次优化状态反馈控制信号上引入扰动项ck+i|k,i=1,…,N，于是双模预测控制律可以表述为

(18)

相应的闭环系统

xk+1=Φdxk+Bdck|k，

(19)

式中：Φd=Ad+BdK。

式(19)又可以扩展成自治状态空间模型

(20)

式中：m表示Bd的行数；E表示Nm×Nm维的单位矩阵的前m行。若存在关于z的可行不变集Ez，定义如下

(21)

则由Schur补定理知，Qz满足下面2个约束：

(1) 不变性

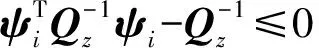
(22)

(2) 可行性

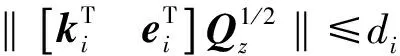
(23)

i=1,…,p，

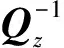
(24)

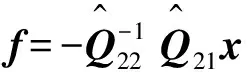
(25)

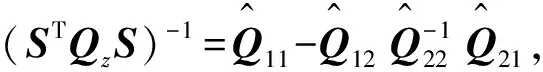
min lg det(SQzST)-1,
s.t. (22),(23).

(26)

只要N足够大，就可以得到满足式(22)，(23)的Qz，于是， 只要f满足z∈Ez，预测轨迹的可行性和不变性便得到满足。

K和Qz确定之后，在整个导引过程中不再改变，因此其计算过程可以离线执行。扰动项ck+i|k专门用来保证预测轨迹的可行性和不变性。K确定之后，在线优化过程中的目标函数(17)可以简化为

J(f)=fTf.

(27)

于是可得下面的导引控制步骤：

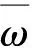
在线计算：在每个采样时刻执行优化

(28)

通过式(18)执行f的第1个元素ck|k，下一时刻重新优化f。

2.3 在线优化问题的计算

在每个采样时刻，x已知的情况下，式(28)定义了一个关于f的椭球面，记为εf。上述优化问题的解若存在，从几何意义上说应当是从原点到椭球面εf的最短距离向量，记为f*，则f*既与εf相交，又与εf在相交点处的切面垂直，即f*既满足式(28)，又满足

f=λ(Q22f+Q21x).

(29)

合并式(29)中关于f的项，得

f=λΓQ21x,Γ=(I-λQ22)-1.

(30)

代入式(28)得关于λ的方程

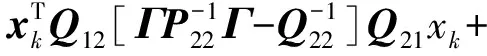
(31)

λ是τ(λ)的唯一负实根(另一实根为正，对应的f具有从原点到εf的最远距离)。因此可以用牛顿-辛普森方法求解。于是在线计算问题概括为

(1)f=0满足式(28)时，取f*=0；

(2) 否则，用牛顿-辛普森方法求解式(31)得λ，代入式(28)得f*。

3 仿真

目标选择高超声速巡航导弹，平均飞行Ma数为6，与水平方向成175°。拦截弹平均Ma数为7.5。双模预测中制导律启动时，目标位置(500,40)km，拦截弹位置(120,30) km，迎着目标平飞。要求中末制导交班距离L=60 km，目标相对于拦截弹导引头的视线与弹轴夹角ξ*=9°。另外要求中制导过程输入不大于0.02 rad/s。

由文献[1]中的方法生成的虚拟目标起始位置为(460,44) km，飞行速度与实际目标相同。

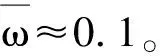
图3和图4分别给出2.1中的常系数导引律和2.2中的双模预测导引律下的拦截弹道轨迹和输入曲线。结果显示，双模预测制导能够很好地保证闭环系统的可行性，并使整体性能指标得到进一步优化，其中常系数次优化导引律的实际性能指标为0.016 2，双模预测导引律0.010 1。

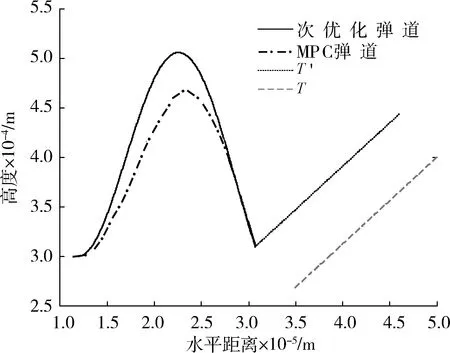
图3 拦截弹道轨迹Fig.3 Missile trajectories for interceptor

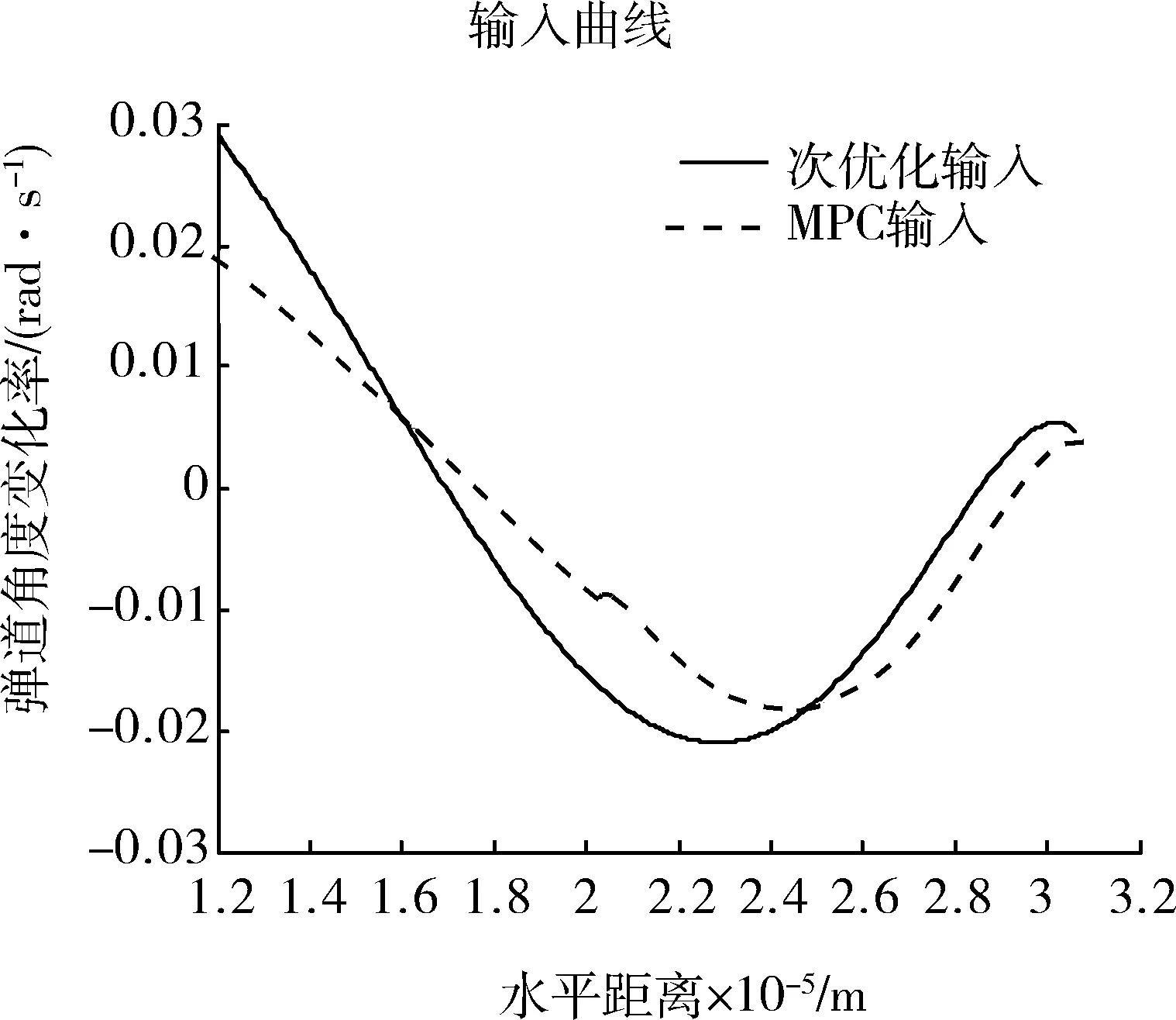
图4 输入曲线Fig.4 Curve for inputs

4 结束语

本文针对大气层内目标拦截弹既要满足末制导侧窗探测对中制导末端时刻，弹目相对距离和位置的要求，又要满足飞行过程中的过载、动压等约束的问题提出了双模预测制导律。该导引律通过引入有限维输入扰动量保证了闭环系统的可行性和稳定性，同时实现对性能指标的进一步优化。仿真结果证明该导引律可以很好地保证过程约束得以满足，并且可以有效减小性能指标值。研究预测制导在拦截弹中制导过程的应用具有重要的理论价值和实践意义。

参考文献：

[1] 李爽, 江涌, 张奕群, 等. 基于虚拟目标的大气层内拦截弹中制导律研究[J]. 航天控制, 2013, 31(3): 27-32.

LI Shuang, JIANG Yong, ZHANG Yi-qun, et al. Research on Midcourse Guidance Law for Interceptor in Atmosphere Based on Virtual Target[J]. Aerospace Control, 2013, 31(3): 27-32.

[2] 李爽, 江涌, 李君龙, 等. 中制导虚拟目标的定位参数研究[J]. 现代防御技术, 2013, 41(3): 48-52.

LI Shuang, JIANG Yong, LI Jun-long, et al. Research on Location Parameters of Virtual Target for Midcourse Guidance[J]. Modern Defence Technology, 2013, 41(3): 48-52.

[3] MAYNE D Q,RAWLINGS J B, RAO C V, et al. Constrained Model Predictive Control: Stability and Optimality[J]. Automatica, 2000, 36(9): 789-813.

[4] KEVICZKY T, BALAS G J. Receding Horizon Control of an F-16 Aircraft: a Comparative Study[J]. Control Engineering Practice, 2006, 14(9): 1023-1033.

[5] 郑立伟, 荆武兴, 张燕. 基于高斯问题的近最优再入预测制导方法研究[J]. 航天控制, 2006, 24(1): 39-42.

ZHENG Li-wei, JING Wu-xing, ZHANG Yan. The Sub-Optimal Prediction Guidance Algorithm for the Reentry Vehicle Based on the Gauss Equation[J]. Aerospace Control, 2006, 24(1): 39-42.

[6] ASHOK J, SIVAN K. Predictor-Corrector Reentry Guidance Algorithm with Path Constraints for Atmospheric Entry Vehicle[J]. Journal of Guidance, Control and Dynamics, 2007, 30(5): 1307-1308.

[7] 张军, 肖余之, 毕贞法. 基于多模型预测的再入飞行器制导方法[J]. 航空学报, 2008, 29(5): 20-25.

ZHANG Jun, XIAO Yu-zhi, BI Zhen-fa. Guidance Method Based on Multi-Model Prediction for Reentry Vehicle[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 20-25.

[8] 呼卫军, 杨业, 周军. 基于外部信息源的临近空间飞行器中制导研究[J]. 航天控制, 2010, 28(2): 23-29.

HU Wei-jun, YANG Ye, ZHOU Jun. Research of Midcourse Guidance Based on External Information Source for Near Space Vehicle[J]. Aerospace Control, 2010, 28(2): 23-29.

[9] KOUVARITAKIS B, ROSSITER J A, SCHUURMANS J. Efficient Robust Predictive control[J]. IEEE Transactions on Automatic Control, 2000, 45(8): 1545-1549.

[10] KOUVARITAKIS B, CANNON M，ROSSITER J A. Who Needs QP for Linear MPC anyway[J]. Automatica, 2002, 38(5): 879-884.

[11] LI Shuang, KOUVARITAKIS B, CANNON M. Improvements in the Efficiency of Linear MPC[J]. Automatica, 2009, 46(1): 226-229.

[12] KOUVARITAKIS B, LI Shuang, CANNON M.A Linear Search Improvement of Efficient MPC[J]. Automatica, 2010, 46(11): 1920-1924.