基于变结构多模型算法的机动目标无源跟踪*
毛云祥,牛朝阳 ,张进
(电子工程学院,安徽 合肥 230037)
0 引言
变结构多模型(variable structure multiple-model, VSMM)算法通过对先验信息以及包含于量测序列的后验信息处理,来确定当前时刻模型集合,基于此模型集进行滤波估计,最后融合输出。VSMM算法的核心是模型集自适应(model set adaptation, MSA);发展高效、通用的MSA是VSMM算法成功的关键。自VSMM算法被提出以后,一系列实用的VSMM算法得到发展和应用[1]。期望模式增广(expected-mode augmentation, EMA)[2]算法是一种高效的变结构多模型算法,它通过对当前模型集中的多个模型加权组合,自适应地生成一个或几个期望模式来近似目标的实际运动模式,这就使它能够用较少数量的模型对机动目标进行有效的跟踪;其任意时刻的模型数目都是固定的,可以看作是基于固定模型集的期望模式增广算法;然而,并不是固定模型集中的所有模型对目标状态估计都有积极影响。可能模型集(likely-model set, LMS)算法通过激活、保留、舍弃等措施自适应选择模型集,在保持交互式多模型(interacting multiple-model ,IMM)算法精度的同时,降低了有效模型集的规模。
基于以上分析,本文将LMS算法的思想引入到EMA算法中,对EMA中的固定模型集进行有效的管理,提出了基于可能模型集的期望模式增广算法,并将其应用于机动目标的无源跟踪中。
1 基于可能模型集的期望模式增广算法
LMS-EMA是一种递推算法,每一个周期(k-1到k时刻)包括3个部分内容:可能模型集确定,期望模式集生成,基于可能模型集和期望模式集的并集的多模估计。

k时刻的增广模型Ek可由不同的方法计算得到,采用基于Mk-1的预测模型概率加权可得
(1)
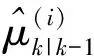
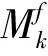
(2)



(3)
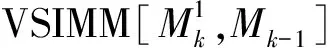

(4)
(5)
(6)
EMA-LMS算法的一个周期如下:
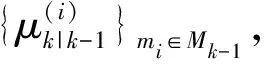



1) 运行VSIMM[Mn,Mk-1]周期。


2 仿真实验
为了验证本文算法的性能,将其应用于实际的无源雷达跟踪机动目标的场景中。选择目标运动模型[11]:
(7)
(8)
针对3维空间中的运动目标进行跟踪。目标以初始状态为
x0=(3×104m,388 m/s,3×104m,161 m/s,8×103m,0 m/s)T,在高度为8×103m的近似水平面内运动。为了躲避高炮打击以及雷达锁定,目标从某一时刻起,以最大加速度在水平面内作蛇形机动[12],轨迹如图1所示。x和y方向的加速度分别为ax和ay,如图2所示。

图1 目标运动轨迹Fig.1 Trajectory of maneuvering target

图2 目标在x和y方向的加速度Fig.2 x and y accelerations
采用基于可能模型集的期望模式增广算法进行跟踪。为了说明该算法的优势,同时给出了IMM、期望模式增广算法(EMA)的跟踪结果,其中,模型数目参数K=8。所有算法均进行500次Monte Carlo仿真实验。这几种多模型算法均采用13个固定模型,模型对应的x,y,z方向的加速度为a,m/s2。
m1:a=(0,0,0)T,m2:a=(30,30,0)T,
m3:a=(-30,30,0)T,m4:a=(-30,-30,0)T,
m5:a=(30,-30,0)T,m6:a=(0,60,0)T,
m7:a=(-60,0,0)T,m8:a=(0,-60,0)T,
m9:a=(60,0,0)T,m10:a=(60,60,0)T,
m11:a=(-60,60,0)T,m12:a=(-60,-60,0)T,
m13:a=(60,-60,0)T.
固定模型集的概率转移矩阵Πf=(πij)设计为
(9)
具有期望模式的转移概率矩阵为Π=(pij),其中,
p1,14=0.01,pi,14=0.05,i=2,…,13,
pjj=πjj-pj,14,p14,j=0.01,j=1,2,…,13,
(10)
Π中的其他元素与Πf中相同(pij=πij)。
比较几种算法的位置和速度的均方根误差如图3所示。
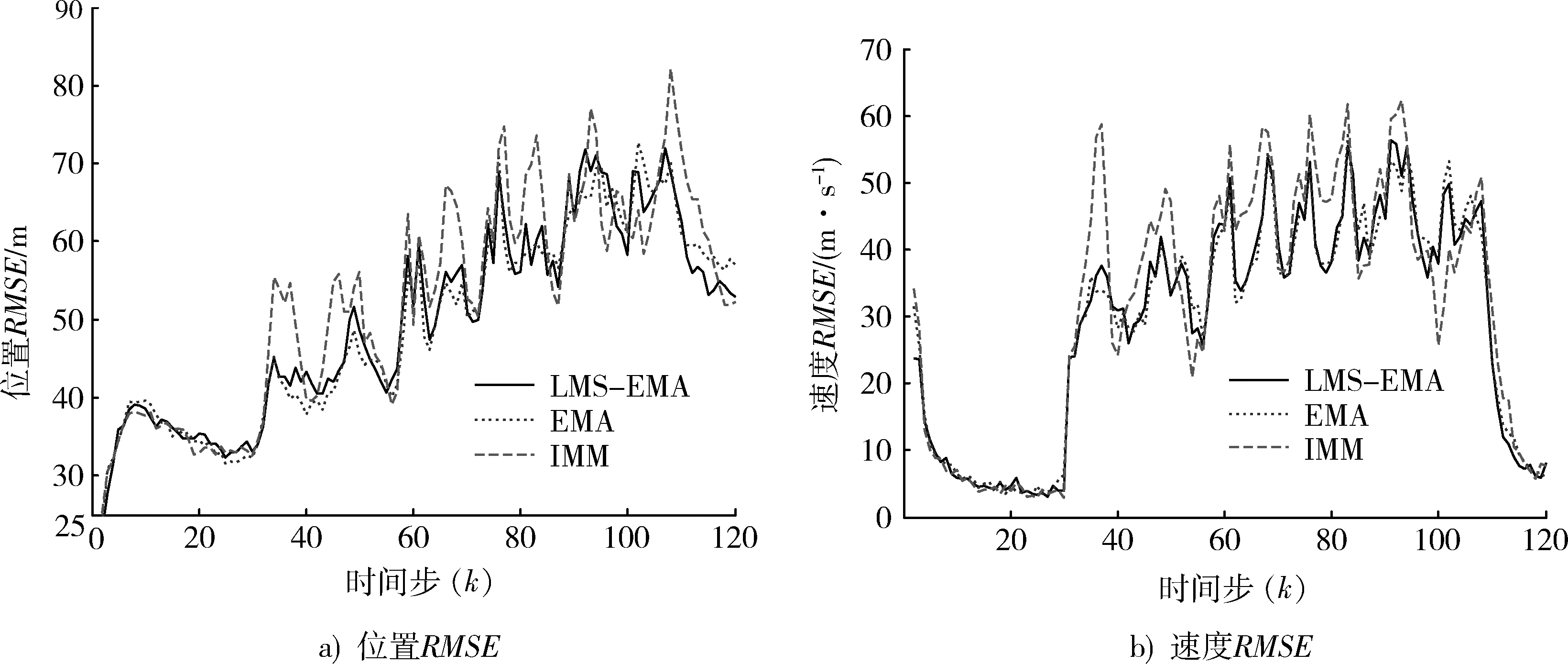
图3 位置和速度的均方根误差Fig. 3 RMS position and velocity errors
从图3可以看出,LMS-EMA和EMA具有基本相同的跟踪精度;LMS-EMA则明显优于IMM算法。原因是IMM算法使用的总模型集是固定网格模型集,而目标运动模式是变化的,经常与任何固定网格模式都不匹配,从而导致跟踪误差较大;LMS-EMA算法通过自适应生成一个期望模式,能够较好地近似目标的运动模式,减小了模式失配,从而降低了跟踪误差。
表1给出了几种算法的性能比较,包括:算法每步迭代所需时间(elapsed time per iteration, ETPI);位置的均方根误差均值(RMSPE);速度的均方根误差均值(RMSVE)。由于目标模式(加速度) 是时变的,不便于比较。从表中可以看出LMS-EMA算法的计算量大大低于IMM,EMA。另外,在平均均方根误差方面,LMS-EMA和EMA相近,明显优于IMM算法。因此,总体来说,LMS-EMA的计算量小;同时保持了EMA算法的精度,是一类高效、精确的跟踪算法。LMS-EMA算法能够对空中蛇形机动的目标进行有效的跟踪。

表1 算法性能Table 1 Performance of IMM, EMA and LMS-EMA algorithm
3 结束语
将本文算法应用于多站无源雷达跟踪空中蛇形机动目标的场景中,仿真结果表明该类算法具有较小的计算量和较高的跟踪精度,同时具备了LMS算法计算量小和EMA算法估计精度高的优点。因此,该类算法非常适合应用于多站无源雷达的机动目标跟踪系统中。
参考文献:
[1] LI X R,JILKOV V P. Survey of Maneuvering Target Tracking Part V: Multiple-Model Methods[J].IEEE Trans. AES, 2005, 41(4): 1255-1321.
[2] LI X R,JILKOV V P,RU J Feng. Multiple-Model Estimation with Variable Structure-Part VI:Expected-Mode Augmentation[J].IEEE Trans.AES,2005, 41(3): 853-867.
[3] SINHA A, KIRUBARAAJAN T,BAR-SHALOM Y. Application of the Kalman-Levy Filter for Tracking Maneuvering Targets[J]. IEEE Trans. AES, 2007, 43(3): 1099-1107.
[4] LI X R. Engineer’s Guide to Variable-Structure Multiple-Model Estimation for Tracking. In Bar-Shalom Y, Blair W D (Eds.), Multiple-multisensor tracking: applications and advance [M]. Vol.Ⅲ, Boston, MA: Artech House, 2000, ch. 10: 529.
[5] LI X Rong,ZHANG Y M. Multiple-Model Estimation with Variable Structure-Part V: Likely-Model Set Algorithm[J]. IEEE Trans. on AES, 2000,36(2): 448-466.
[6] JIKOV V P,D S. Angelova Semerdjiev. Mode-Set Adaptive IMM for Maneuvering Target Tracking[J].IEEE Trans,1999,35(1):343-350.
[7] SINHA A ,KIRUBARAJAN T,BAR-SHALOM Y. Application of the Kalman-Levy Filter for Tracking Maneuvering Targets[J]. IEEE Trans.AES,2007,43(3):1099-1107.
[8] YANG C,BAKICH M,BLASCH E P.Pose Angular-Aiding for Maneuvering Target Tracking[C]∥Proceedings 2005 International Conference on Information Fusion, 2005:576-582.
[9] Oliver Payne,Alan Marrs.An Unscented Particle Filter for GMTI Tracking[C]∥ 2004 IEEE Aerospace Conference Proceeding,2004:1869-1875.
[10] JULIER S J,UHLMANN J K.Unscented Filtering and Nonlinear Estimation[J]. Proc. IEEE,2004,92(3): 401-422.
[11] JULIER S J,UHLMANN J K,DURRANT-WHYTE H F.A New Method for The Nonlinear Transformation of Means and Covariances in Filters and Estimators[J].IEEE Trans. Automatic Control,2000,45(3):477-482.
[12] LI X R,JILKOV P. Multiple-Model Estimation with Variable Structure-Part VI: Expected-Mode Augmentation[J]. IEEE Trans on AES,2005,41(3):853-867.

