红外低轨星座对弹道目标动态覆盖性能分析*

关永峰，谢恺，库锡树，刘菊荣

(1．国防科技大学 电子科学与工程学院，湖南 长沙 410073；2. 陆军军官学院，安徽 合肥 230031)

0 引言

红外低轨星座是未来弹道导弹防御系统的重要组成部分。该星座通过多星、多传感器协同工作实现对弹道目标的跟踪监视；每个卫星搭载一台捕获相机和一台跟踪相机，扫描相机采用红外短波波段对地进行大视场扫描捕获主动段目标，捕获目标后将目标交接给采用中长波红外波段的小视场跟踪相机，以对中段冷弹头进行接续跟踪，从而实现对目标的全程跟踪监视[1-6]。

捕获相机能否捕获到主动段目标是整个星座系统发现目标的关键，而星座对主动段的覆盖则是系统捕获主动段目标的前提。红外低轨星座对目标主动段的覆盖分析对于星座、传感器的设计具有重要意义，同时，对于攻击方寻找系统覆盖盲区进行导弹突防也有一定的应用价值。

传统的星座覆盖分析领域主要是对地遥感、移动通信、GPS定位等，一般采用网格点数值仿真分析星座对地面的静态覆盖。而对于具有高速运动特性的弹道目标主动段，星座对其覆盖分析则应考虑对全球立体空域的覆盖。

目前尚无文献给出低轨红外星座对弹道目标主动段的覆盖方法。本文提出一种低轨红外星座对弹道目标主动段覆盖分析方法；该方法将网格点覆盖分析的思想拓展到弹道目标主动段的覆盖分析当中，以每条具体的主动段弹道作为相应的“网格点”；通过分析星座的覆盖特点，将利用静态网格点分析星座全球覆盖和对特定区域的弹道目标主动段覆盖相结合。最后运用STK软件进行覆盖实例分析，根据实例覆盖分析结果，提出覆盖间隙开始时间的概念，以有效衡量红外低轨星座对弹道目标主动段的覆盖性能。

1 覆盖分析方法

1.1 覆盖分析思路

星座对主动段目标的覆盖分析仅考虑静态覆盖分析是不充分的。目标具有不同的发射时间、弹道特性(射向、射程、燃料推进策略等弹道影响因素)，且主动段目标和星座本身处于高速运动状态，这使得星座对主动段目标的覆盖是个动态变化过程。红外低轨星座对弹道目标主动段覆盖分析所面临的是一个多维空间问题(目标发射点位置、发射时间，射向，主动段弹道特性等)。依据传统的静态网格点覆盖分析思想，可在该空间各维分别离散取值，各维的各离散点构成的每个组合即为单个弹道目标的主动段弹道，将此作为“网格点”，进行多影响因素下的动态覆盖分析。但是，相对于网格点的覆盖计算，该方法的计算量随着空间维数和各维的离散取值点个数增大而以线性增加，使得主动段目标覆盖分析计算量太大。本文将通过分析星座覆盖特点，寻求空间降维或减少各维数据取值区间，在保证覆盖分析有效性的同时减少计算量。

弹道目标的主动段弹道特性相当复杂，不失一般性本文考虑以最小能量发射推进的弹道导弹。对弹道目标主动段的覆盖分析可归结为一个5维空间问题(发射点位置x/y，发射时间t，射向θ和射程L)，在该5维空间的每一维上离散取值以进行多影响因素下的覆盖分析，如式(1)。

(1)

式中:Pcov,φ分别为星座覆盖性能和影响因素矢量。

覆盖的影响因素有如下约束：

(2)

如何选择式(2)中的各约束边界取值是本文覆盖分析方法的核心。对于导弹射向，θ在[0°,360°]范围内离散取值是显而易见的；对于射程，本文取典型的800 km和2 000 km 2种不同射程。因此，分析的重点在于覆盖区域和覆盖周期的选择，不妨令t0=0。

图1给出星座覆盖示意图。β为扫描相机半视场角；h为距离地面的高度。

图1 星座覆盖示意Fig.1 Sketch of constellation coverage

图1中，覆盖间隙呈现倒锥形状，可以看出，高度越低的区域星座扫描相机对其覆盖性能越好。红外低轨星座初步设计为部属25～30颗卫星以实现全球覆盖[7]，因此可首先计算星座的一重静态覆盖情况，分析可能出现的覆盖间隙。在星座一重覆盖到的区域内则不必进行弹道目标的主动段覆盖分析，从而减少覆盖分析范围。

该方法在不降低覆盖分析准确性基础上，从减少覆盖分析计算量的角度出发，根据星座对地、对距地面一定高度空域的覆盖分析情况，结合星座构型周期性变化的特点，选择能代表全球覆盖间隙的覆盖分析周期和小范围典型区域，在该小范围区域内部署弹道导弹，统计分析不同射向、不同发射时间、不同类型导弹发射情况下，星座对主动段目标的覆盖(覆盖间隙)情况。其中，覆盖分析周期和覆盖分析区域的选择是本文方法的2个关键。

1.2 覆盖区域和周期的选择

红外低轨星座是一个全球覆盖星座。实现全球持续覆盖的星座一般采用Walker星座，文献[1]所设计的天基红外低轨星座即采用Walker-δ星座。因此，本文将以Walker-δ星座为例分析星座覆盖特点。假定Walker-δ星座参数为T/P/F/h/i，T，P，F分别为星座卫星总数、轨道平面数、相位参数，h和i则分别为轨道高度与轨道倾角。

星座覆盖间隙具有周期性变化特点。Walker星座各卫星的连续运动，使得覆盖空隙连续地变化。同时，Walker星座构型的周期变化，使得星座的覆盖空隙呈现与星座构型一致的周期性。综合考虑覆盖空隙的连续性和星座构型变化周期，得到星座覆盖空隙的变化周期如下：

Tperiod=Tcir/(T/P),

(3)

式中:Tperiod为星座覆盖空隙变化周期;Tcir为轨道周期。

星座各卫星以圆轨道运行，如下式[8]：

(4)

式中：rcir为轨道半径；μ为地球引力常数。

在一个覆盖间隙周期内，由于地球由西向东自转，覆盖间隙区域也将由东向西移动一段距离。覆盖间隙区域位置移动的经度差为

ΔLlong=2π(Tperiod/Tday)，

(5)

式中：Tday为一天的时间周期。

另一方面，星座覆盖空隙具有对称性特点。这是由Walker-δ星座本身的对称性所决定的。具体的对称形态与星座的相位参数有关，但总体上，星座的覆盖空隙呈现南北纬对称，每固定经度间隔周期对称，而对单个覆盖空隙，其在一个变化周期内的形状变化也是对称的。

综上所述，星座对全球空域的覆盖有3个特点：①覆盖空隙的形状时刻变化，变化具有周期性，在单个周期内形状对称变换；②覆盖空隙在不断变换其形状的同时也不断在东西方向上移动，这是由于地球的自转；③对于相对地球均匀对称分布的星座，其覆盖空隙也是相对地球对称的。

依据上述星座覆盖特点，覆盖分析周期可选择为覆盖空隙变化周期的一半，即

Tcov=Tperiod/2.

(6)

在进行覆盖分析区域选择时，首先通过测试观察星座对地或对空域的覆盖情况，综合考虑覆盖间隙的周期性和对称性特点，选择Tcov周期内出现覆盖间隙的典型区域作为覆盖分析区域。根据覆盖空隙的对称性和周期性，完全可以推知其他对称的覆盖间隙区域范围内的主动段弹道目标覆盖情况。本文限于篇幅，选择覆盖空隙最大的区域作为目标主动段覆盖分析区域。

1.3 覆盖分析流程

利用STK/Coverage模块、object access功能计算星座对空间区域/弹道目标主动段的覆盖[9]。采用Matlab软件和STK/Matlab程序接口，进行星座对弹道目标主动段的覆盖分析。图2给出了覆盖分析流程图。

所采用的STK/Matlab，Connect主要命令如下：

(1) stkNewObj，新建/调整星座、相机参数；

(2) stkSetPropBallistic，设置/调整弹道；

(3) stkConnect，STK/Matlab函数调用；

(4) Access，星座对弹道的覆盖计算命令。

2 覆盖实例分析

本节根据具体的低轨红外星座和扫描相机参数，对上述覆盖分析方法进行实例演示分析。

2.1 星座和传感器参数

采用文献[1]的红外低轨星座和扫描相机参数。扫描传感器采用对地锥扫方式[10]，半视场角β=53.41°，卫星对导弹最低探测高度10 km。星座参数如表1所示。

图2 覆盖分析流程Fig.2 Flowchart of coverage analysis

表1 星座参数Table 1 Constellation parameters

TPFh/kmi/(°)28421 59677.8

覆盖分析所采用的2种典型弹道目标主动段弹道，其主要参数如表2所示[11-12]。

表2 弹道参数Table 2 Ballistic parameters

2.2 覆盖区域和周期选择

依据表2，2 000 km射程导弹关机点高度为130 km，据此首先分析星座对130 km高度处的全球覆盖。图3给出星座瞬时覆盖示意图。

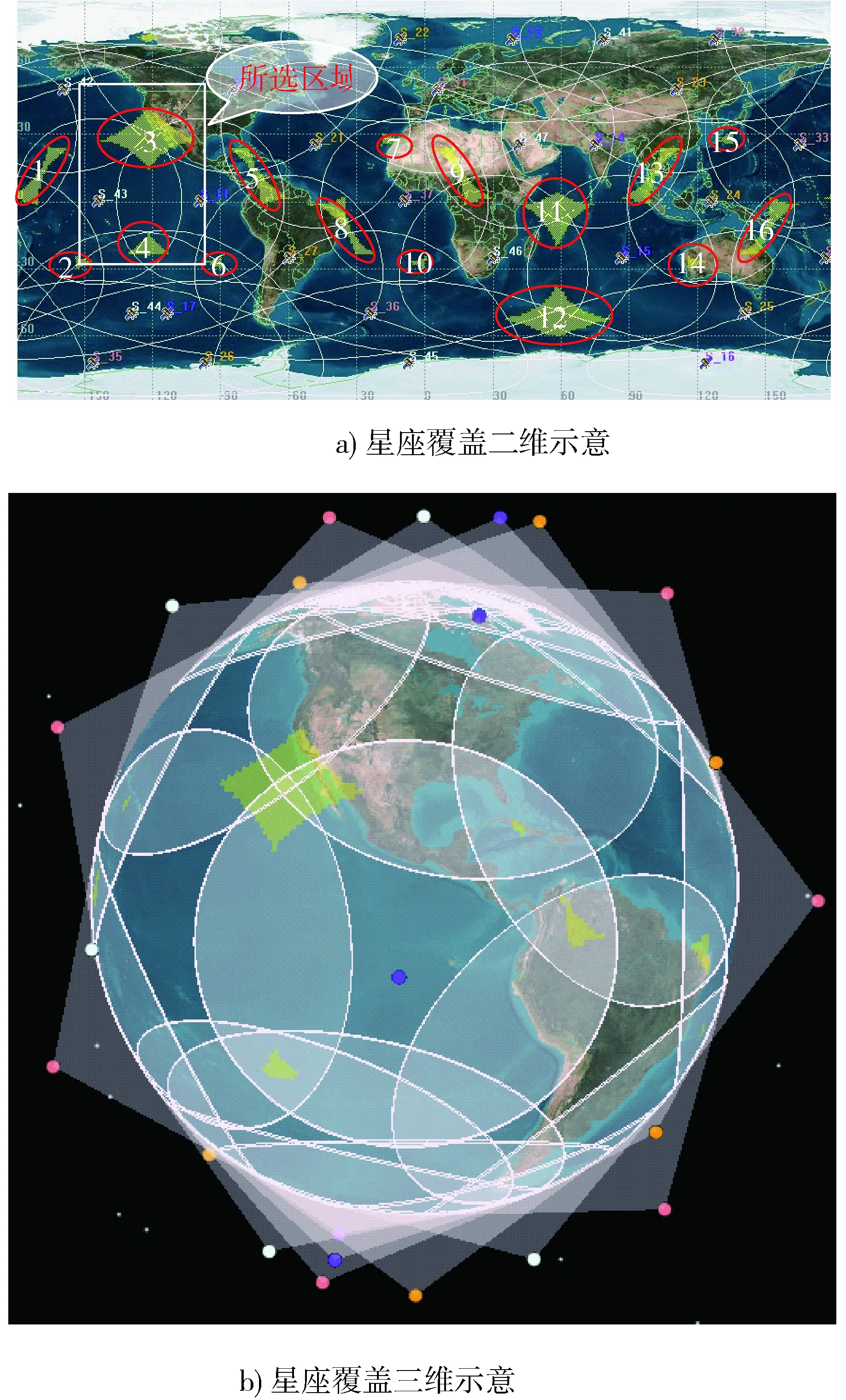
图3 星座瞬时覆盖示意Fig.3 Constellation instantaneous coverage

图3中出现16个覆盖空隙，标识3,4,11和12的几个部分为较大的覆盖空隙。由图3可看出星座覆盖空隙形状的南北对称和随经度间隔变化的周期性。

依据式(3)，(5)分别得到覆盖间隙周期Tperiod=1 012.4 s，一个覆盖间隙周期覆盖空隙移动的经度差ΔLlong=4.2°。

图4给出一个覆盖间隙周期内星座对局部区域(纬度：-60°～60°；经度：-90°～-150°)的覆盖空隙变化。图4a)覆盖时刻记为0 s，则图4b)～4h)的覆盖时刻分别为144,288,432,576,720,864,1 012.4 s。

图4 局部区域覆盖空隙Fig.4 Coverage gap of local areas

由图4a)～4h)看出，在一个覆盖间隙周期内，覆盖空隙连续变化且其形状是对称的，如4b)～4f)；同时，由于地球自转，覆盖空隙整体由东向西移动，如4a)和4h)。图4的结果验证了1.2节分析的覆盖空隙的特点。

根据星座对距离地面130 km处的全球静态覆盖分析，选择目标主动段覆盖分析区域ΔA：纬度:-15°～65°，经度:-100°～-150°，如图3中的方框所在区域；选择目标主动段覆盖分析周期Tcov=506.2 s。

2.3 覆盖结果与分析

在所选区域ΔA和覆盖分析周期Tcov内，纬度和经度每隔3°×3°设置导弹发射点(x,y)，所有导弹(包括2种不同射程导弹)射向θ每变化20°、发射时间每隔120 s齐射一次，统计分析星座扫描相机对所有目标主动段弹道的覆盖情况。

每种射程导弹均分别设置36 299条主动段弹道。覆盖统计结果如下。

(1) 对800 km和2 000 km射程弹道目标：出现覆盖间隙的个数分别为101枚、3 851枚，分别占总数的0.28%和10.61%；

(2) 出现覆盖间隙的目标，只出现一次覆盖间隙的情况为100%，且覆盖间隙均持续到导弹主动段关机。

星座对主动段目标覆盖对系统目标检测性能的影响，主要体现在2个方面：星座扫描相机对主动段目标的可观测时间和观测是否连续。由上述统计结果，对于2种类型导弹，覆盖间隙若存在则均只出现一次，即不出现多个间隔的覆盖间隙情况；且覆盖间隙一旦出现，均持续到目标关机，这从图1的倒锥形覆盖空隙可明显看出。此时，在统计意义下，在所给星座和相机参数下，星座对单个目标主动段的覆盖间隙仅仅是单次、连续的，这意味着星座扫描相机对主动段目标的观测是连续的，而覆盖间隙开始时间界定了星座对主动段目标的可发现时间，从而影响星座捕获传感器到跟踪传感器交接的时机选择。因此，星座对主动段目标的覆盖间隙开始时间tgi是星座覆盖影响系统检测性能的核心因素，可作为红外星座对目标主动段覆盖性能的衡量指标。

表3为覆盖间隙开始时间统计。图5为覆盖间隙开始时间统计累积分布图。

表3 覆盖间隙开始时间统计Table 3 Statistic results of coverage gap initial time

表3中，s,tbp分别为导弹射程、主动段飞行时间；tmingi，tmeangi，σtmeangi分别为最小覆盖间隙开始时间、平均覆盖间隙开始时间和平均覆盖间隙开始时间标准差。

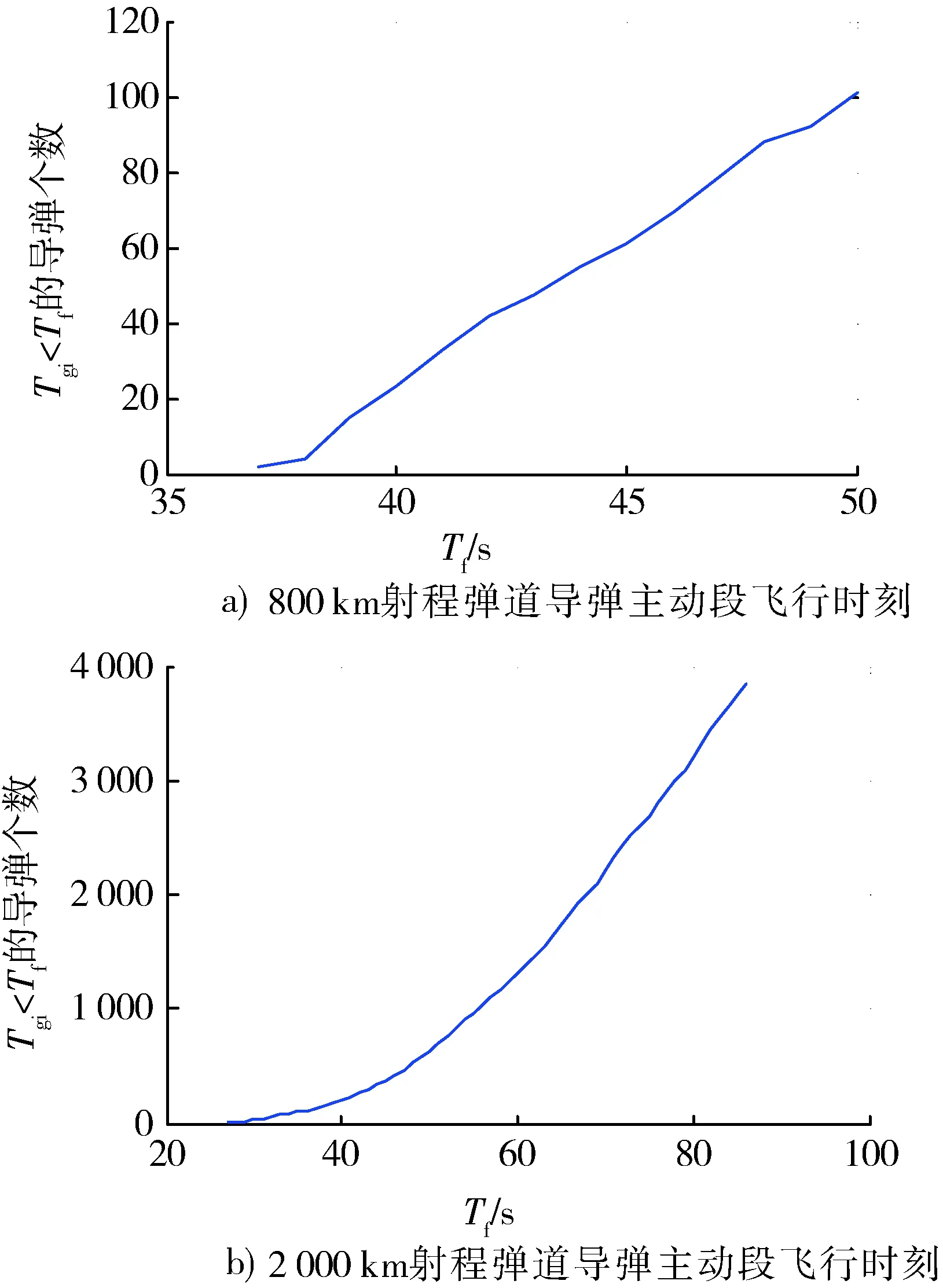
图5 覆盖间隙开始时间分布Fig.5 Distribution of initial coverage gap

依据表3和图5覆盖统计结果，在给定的仿真条件下，星座对800 km射程和2 000 km射程导弹的主动段平均持续观测时间分别为44 s和76.3 s，表明星座对2种类型导弹的主动段捕获并交接给跟踪相机的时间不能超过目标发射后44 s和76.3 s。

若星座欲对所有导弹主动段进行检测截获，则星座系统对2种射程导弹主动段发现时间分别不能低于37 s和27 s。

2.4 覆盖分析与星座/传感器设计的改进

若认为星座对不同目标的37 s和27 s的最小覆盖间隙开始时间对系统目标发现时间提出较高的要求，可考虑对星座/传感器参数进行改进以提高覆盖性能，缓解系统信息处理的压力。

改进扫描相机参数，将扫描相机半视场角β提高为54.5°，仍然采用本文方法分析覆盖性能。在相同的覆盖区域和分析周期内，统计覆盖间隙开始时间如表4所示。

表4 覆盖间隙开始时间统计Table 4 Statistic results of coverage gap initial time

表4中，对于800 km导弹，星座对其主动段完全覆盖，而对于2 000 km导弹主动段，最小覆盖间隙和平均覆盖间隙开始时间均有大幅提高，分别达到64 s和79.8 s，有效缓解星座系统信息处理压力。

2.5 运行时间分析

在计算实例中，采用Intel(R) Core2 Quad CPU Q6600 2.40G，内存为2G，程序运行时间Δt为18 440 s，约5 h；每条主动段弹道的分析时间约为0.254 0 s。

在所分析的覆盖五维空间中，覆盖分析的计算量将随着空间维数和各维离散取值点个数增大而线性增加。

例如：在其他相同条件下，若对全球范围内的主动段目标进行覆盖，计算时间Δtglobal为

Δtglobal=Δt(ΔSglobal/ΔS)=9.207 5Δt，约47 h。上式中，ΔSglobal/ΔS为全球与特定区域的面积之比。

在其他相同条件下，若对24 h内的特定区域主动段目标进行覆盖，计算时间Δtday为

Δtday=Δt(Δt24/Δt)=170.751 0Δt，

约874.62 h。式中Δt24/Δt为24 h覆盖周期与实例中的覆盖周期之比。

对比上述2个例子与本文实例的计算时间可看出，由于本文利用了星座覆盖的空域对称性和时域重复性，将全球静态网格点覆盖和对特定区域特定时间内的弹道目标主动段覆盖相结合，大大降低了星座对主动段目标覆盖的分析时间，使得方法的工程实用性很高。

3 结束语

红外低轨星座对弹道目标主动段的覆盖，是整个星座系统检测捕获目标的前提。覆盖分析的对象是快速运动的主动段弹道目标，本文总结并提取出影响星座覆盖的5个影响因素，借鉴传统的网格点覆盖思路，将每条主动段弹道作为覆盖分析的“网格点”。考虑到网格点覆盖分析的计算量大的特点，通过分析星座覆盖空隙的空域对称性和时域周期性，在全球静态网格点覆盖分析基础上，合理缩小动态覆盖分析的周期和覆盖分析区域，在保持覆盖分析效果的同时减少计算量。

结合STK软件给出覆盖分析实例，并对覆盖结果进行分析，提出覆盖间隙开始时间概念，可有效衡量星座对弹道目标主动段覆盖的性能。平均覆盖间隙开始时间可总体衡量星座扫描相机对主动段目标的平均发现时间要求，最小覆盖间隙开始时间界定星座全球覆盖必须满足的最早目标发现时间。

本文提出的方法对于设计和评价红外低轨星座具有一定的参考价值，同时对于弹道导弹突防具有工程实用价值。

参考文献：

[1] Irene A Budianto, John R Olds. A Collaborative Optimization Approach to Design and Deployment of a Space Based Infrared System Constellation[J]. IEEE NAECON,2000(1):385-393.

[2] Brian L Morgan. Exploratory Model Analysis of the Space Based Infrared System (SBIRS)[R]. Low Global Scheduler Problem. DA309027,1999.

[3] Jim Shoemaker. Space Tracking and Surveillance System (STSS) Block 06 Sensor Suite[EB/OL]. Raytheon Company Space and Airborne Systems(2012-04-06)[2013-01-01].http:∥www.raytheon.com.

[4] Carl G Pfeiffer. Background Adaptive Target Detection and Tracking with Multiple Observation and Processing Stages[P]. U.S.Patent, No.5960097,1999.

[5] 谢恺，韩欲生，薛模根，等. 低轨红外预警星座无源定位精度分析[J]. 信号处理，2008, 24(3)：343-348.

XIE Kai,HAN Yu-sheng, XUE Mo-gen, et al. Analysis of Passive Location Accuracy in LEO Infrared Early Warning Constellation[J]. Signal Processing, 2008, 24(3)：343-348.

[6] 谢恺，韩欲生，薛模根，等. 基于遗传算法的低轨天基雷达星座设计[J]. 信号处理，2008, 24(2)：233-236.

XIE Kai, HAN Yu-sheng, XUE Mo-gen, et al. LEO Space-Based Radar Constellation Design Based on Genetic Algorithm[J]. Signal Processing, 2008, 24(2)：233-236.

[7] Northrop Grumman. Space Tracking and Surveillance System (STSS)[EB/OL].U.S.Missile Defense Agency(2012-01-05)[2013-01-01].http:∥ww.nti.org/.

[8] BateRoger R,Mueller Donald D, White Jerry E. Fundamentals of Astrodynamics[M]. New York: Dover Publishing,Inc.,1971.

[9] AGI. STK help Doc[EB/OL].(2012-02-19)[2013-01-01]. http:∥www.stk.com.

[10] Lacy G Cook, Bryce A Wheeler. Ultra Wide Field of View Scanning Surveillance Optical System[P]. U.S.Patent, No.5347391,Sep.1994.

[11] Alebrt J Perrella Jr. Cueing Performance Estimation Using Space Based Observations During Boost Phase[R]. ADA320125, Sep.1996.

[12] Florios Bardanis. Kill Vehicle Effectiveness for Boost Phase Interception of Ballistic Missiles[D].Monterey,Califomia,USA:Naval Postgraduate,Jun,2004.