基于成像质量的进动参数估计*
赵会宁,贺思三,龙戈农,张永顺
(空军工程大学 防空反导学院,陕西 西安 710051)
0 引言
弹道导弹防御系统中的目标识别技术是当前研究热点,而弹道中段射程和飞行时间占全弹道的80%~90%以上,可以实现较长时间的识别与拦截,是导弹防御的关键阶段。弹头在中段可释放各种假目标进行欺骗和干扰,使中段拦截面临巨大挑战,如何有效识别真、假弹头是中段防御的核心问题之一。自2000年以来,随着对目标微动效应的深入研究,应用微动特征识别目标引起了研究人员的广泛关注,进动作为空间椎体目标的重要运动特征,为弹道目标中段真假弹头识别提供了新的解决手段。
对中段目标进动特性的研究主要分为2类:中段进动弹头运动及雷达回波建模[1-2]与基于进动参数估计[3-9]。在运动建模方面,主要关注于如何在考虑平动、自旋、进动的基础上对中段目标的运动进行描述,并分析其微多普勒特征。在进动参数估计方面,所关注的参数包括进动周期及进动角2个参数。进动周期参数主要从回波信号的周期特性获得,参数估计方法物理意义明确;而进动角参数估计算法则相对复杂。在研究初期,所提进动角参数估计算法往往需要先验信息,如文献[3-5]要求知道目标的结构先验信息,文献[6]要求知道雷达视线角的先验信息。为了克服先验信息的限制,文献[7-8]分别提出了基于ISAR序列和距离像序列的进动角估计方法,这2种算法要求雷达入射方向发生较大变化,所需观测时间较长;文献[9-10]研究了基于多站观测的进动角估计算法,利用多站观测信息的互补性,它们可在较短时间内(1个周期)实现无先验信息条件下的进动参数估计。
本文对进动参数估计展开深入研究,提出了基于成像质量的进动参数估计思想,设计了相应的搜索参数降维方法,使得只需通过对进动角的一维搜索就可得到进动参数的估计。该算法能够在没有先验信息的条件下仅利用单站雷达的观测信息在一个进动周期内实现进动参数估计。
1 弹头目标宽带散射特性及进动模型
常见的弹头外形有平底锥弹头、球底锥弹头、平底锥柱弹头及球底锥柱弹头,本文以平底锥弹头为例对进动目标参数估计进行研究。
1.1 弹头目标宽带散射特性分析
平底锥弹头结构如图1所示。

图1 平底锥弹头模型Fig.1 Model of conical warhead
图1中rq为球冠半径,ξ为半锥角,R为底面半径,b为球冠中心到底面边缘的距离,φ为雷达视线与锥体对称轴的俯仰角。对于锥形弹头而言,当底部半径一定时,半锥角减小则弹头的RCS、锥面最大气动压力、气动加热率和气动阻力都将减少,因此,适当减小半锥角有利于提高弹头飞行性能;但半锥角减小将使弹头加长,且弹头加长后侧面积随之增加,弹头防热与承力结构的质量也要增加。综合考虑各种因素,弹头半锥角可取范围一般为7°~11°[11]。由此可得如下性质:
性质1:弹头半锥角ξ可取范围一般为7°~11°。

性质2:目标在雷达视线方向的投影长度将随着φ的增大而减小。

性质3:在此角度变化范围内,对数据成二维像后横向距离(或纵向距离)差别最大2个散射中心的连线对应了靠近雷达视线方向锥面所在位置。
性质3是由于目标的遮挡效应造成的:当雷达视线方向指向一侧时,另一侧被遮挡,从而只有靠近雷达视线方向弹面上的等效散射中心才可见,具体内容可参考文献[12]。
1.2 中段目标进动模型
由于平底锥弹头是旋转对称的,其散射特性只与俯仰角有关,而与方位角无关,因此只需考虑φ的变化对散射特性的影响。对于中段进动目标,假设雷达视线方向在平动坐标系中的俯仰角为γ,进动角速度为ωP,进动角为θP,雷达视线方向在平动坐标系中的俯仰角为γ,初始方位角为φP,可得俯仰角φ随时间的变化为[3]
cosφ(m)=cosγcosθP+sinγsinθPcos(ωPmTr+φP),
(1)
式中:Tr为雷达脉冲周期;m为采样时刻。
从而可得
φ(m)=arccos[cosγcosθP+sinγsinθPcos(ωPmTr+φP)].
(2)
根据式(2)可知,进动弹头的角度变化具有如下性质:
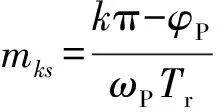
2 基于成像质量的进动参数估计
利用高分辨雷达对进动弹头观测时,其回波可表示为
ycosφ(m))}dxdy,
(3)
式中:D为目标所在区域;I(x,y)为目标的散射系数;ki=2fi/c为波数,其最小值为kmin,最大值为kmax;f为雷达频率;c为光速。
滤波逆投影算法直接利用极坐标格式数据再现目标图像,可实现目标的精密成像,其离散化的成像算法可表示为
exp(j2πkmin(xsinφ(m)+ycosφ(m))).
(4)
该算法直接利用极坐标格式数据对目标散射强度分布进行重构,只有当设定角度变化与实际角度变化一致时,才能得到最好的图像效果。基于此性质,弹头的进动参数可通过下式进行估计:
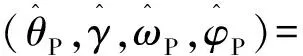
(5)

(6)
理论上说,通过对式(5)的优化可估计进动参数。但滤波逆投影算法快速算法本身计算量大,且直接对式(5)进行优化需进行四维搜索,总运算量非现有计算能力可实现,需要对搜索参数降维处理。
2.1 基于轴对称特性的ωP,φP估计
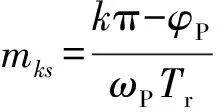
(7)
式中:Imag(F)为对数据进行二维傅里叶变换所得成像结果。根据φ(m)的轴对称性质,可知CP(m)将每隔半个周期出现一个峰值,且峰值位置对应时刻的相位为kπ,雷达回波关于此时刻左右对称。
不妨设经过上述处理后估计出2个相邻对称轴对应采样时刻分别为m1,m2,从而可得ωP与φP的估计为
(8)
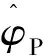
2.2 进动角估计
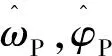
(9)
式(9)表明通过二维搜索可得到θP与γ的估计,考虑到滤波逆投影算法本身运算量大,下面基于弹头目标的散射特性及结构特性进一步将参数搜索降至一维。
一般来说,进动角度比较小,通常为5°~10°,式(2)可作如下近似:
φ(m)≈γ-θPcos(ωPmTr+φP).
(10)
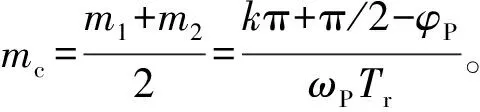
φ(m)≈γ+θPsinωP(m-mc)Tr+kπ≈
(11)
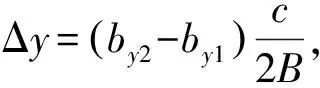
根据图2可知,雷达视线方向可表示为φ=φl-ξ,其中φl为雷达视线方向与可见弹面的夹角,而在[mka-L2,mka+L2]段数据的中心角为φ≈γ,从而可得:
(12)
式(2)中包含了Δθ与ξ2个未知参数。根据性质(1),半锥角ξ可选范围很小,不妨将其设为固定值ξ=9°;而在设定θP的情况下,Δθ可根据所选L2的长度由式(10)计算得到
Δθ≈2θPsinωPL2Tr.
(13)

图2 平底锥弹头的φ,φl,ξ关系Fig.2 Relationship between φ,φl,ξ for conical warhead
上述分析表明,在设定θP的情况下,γ与θP存在对应关系,式(9)可进一步简化为
(14)
3 仿真试验
在本节仿真试验中,均取Tr=0.005 s,L1=30,L2=roundm2-m1/4,在进行估计时设定半锥角为9°,其中round为取整函数。
设平底锥参数为R=0.6 m,rq=0.075 m,b=3.067 m,利用电磁计算软件计算其在0°~180°俯仰角下10 ~12 GHz频率范围内的宽带回波数据,计算时角度间隔为0.2°,频率间隔为30.3 MHz。设置进动参数为γ=50°,θP=7°,φP=π/2,进动周期为2 s,观测时间为2 s。基于弹头电磁计算数据,通过角度的一维插值得到计算俯仰角处对应数据,并加入噪声使总体信噪比为0 dB,其距离像序列如图4a)
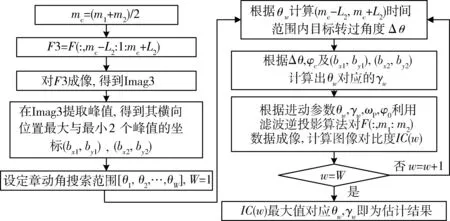
图3 基于成像质量的进动参数估计流程Fig.3 Precession parameters estimation procedure based on image quality
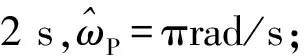
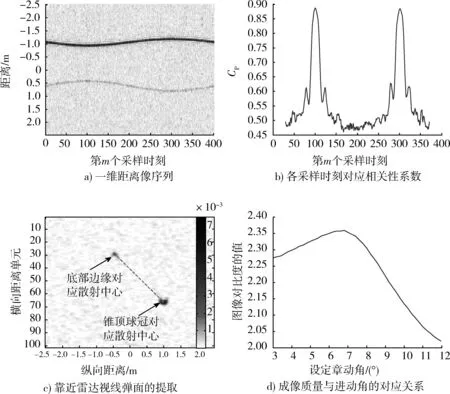
图4 平底锥弹头的进动参数估计Fig.4 Precession parameters estimation for conical warhead

图5 误差对进动角估计的影响Fig.5 Error influence for precession angle estimation
4 结束语
本文首先对弹头目标的宽带散射特性进行了分析,指出弹头目标在雷达视线方向上的投影长度将随着俯仰角的增大而减小,且其二维成像结果的强散射中心分布在靠近雷达视线方向的弹面上;然后基于旋转对称弹头的进动模型,提出了一种基于成像质量的进动参数估计算法,设计了相应的搜索参数降维流程,使得只需通过对进动角的一维搜索就可得到进动参数估计。该算法合理挖掘了弹头的结构特性及散射特性,可在一个进动周期内实现未知结构尺寸的平底圆锥弹头的进动参数估计。
参考文献:
[1] 马梁,刘进,王涛,等. 旋转对称目标滑动型散射中心的微Doppler特性[J].中国科学, 2011, 41(5):605-616.
MA Liang, LIU Jin, WANG Tao, et al. Micro-Doppler Characteristics of Sliding-Type Scattering Center on Rotationally Symmetric Target[J]. Sience China, 2011, 41(5):605-616.
[2] 李松,冯有前,刘昌云,等.弹道导弹微动模型及微多普勒特征研究[J]. 现代防御技术,2011,39(6):85-116.
LI Song, FENG You-qian, LIU Chang-yun, et al.Resarch of Micro-Motion Model and Micro-Doppler of Ballistic Missile[J].Modern Defence Technology, 2011,39(6):85-116.
[3] 贺思三,周剑雄,付强. 利用一维距离像序列估计弹道中段目标进动参数[J].信号处理,2009,25(6):925-929.
HE Si-san, ZHOU Jian-xiong, FU Qiang. Using HRRP Sequence to Estimate the Precession Parameters of Midcourse Target [J]. Signal Processing, 2009, 25(6): 925-929.
[4] 朱玉鹏,王宏强,黎湘,等. 基于一维距离像序列的空间弹道目标微动特征提取[J]. 宇航学报, 2009, 30(3):1133-1140.
ZHU Yu-peng, WANG Hong-qiang, LI Xiang, et al. Micro-Motion Feature Extraction of Spatial Ballistic Target Based on HRRP Dynamic Sequence[J]. Journal of Astronautics, 2009, 30(3): 1133-1140.
[5] 李康乐,姜卫东,黎湘. 弹道目标微动特征分析与提取方法[J]. 系统工程与电子技术,2010,32(1):115-118.
LI Kang-le, JIANG Wei-dong, LI Xiang. Micro-Motion Feature Analysis and Extraction Methods for Ballistic Targets[J].Systems Engineering and Electronics,2010,32(1):115-118.
[6] 雷腾,刘进忙,余付平,等.基于时间一距离像的弹道目标进动特征提取新方法[J].信号处理,2012,28(1):73-79.
LEI Teng, LIU Jin-mang, YU Fu-ping, et al. A New Procession Signature Extraction Method of Ballistic Target Based on Range-Profile[J]. Signal Processing, 2012, 28 (1):77-83.
[7] 金光虎,朱玉鹏,高勋章,等.基于一维像序列的中段雷达目标进动特征提取[J]. 信号处理,2009,25(5):771-776.
JIN Guang-hu, ZHU Yu-peng, GAO Xun-zhang,et al. Precession Feature Extraction of Midcourse Radar Target Based on HRRP Series[J].Signal Processing, 2009,25(5):771-776.
[8] 颜维,孙文峰,钱李昌,等.基于一维像序列的弹道中段目标进动特征提取[J]. 空军雷达学院学报, 2011,25(2):87-96.
YAN Wei, SUN Wen-feng, QIAN Li-chang, et al. Precession Feature Extraction of Ballistic Midcourse Target Based on HRRP Sequences[J]. Journal of Air Force Radar Academy, 2011, 25(2):87-96.
[9] 艾小锋,李永祯, 赵锋, 等. 基于多视角一维距离像序列的进动目标特征提取[J].电子与信息学报, 2011, 33(12):2846-2851.
AI Xiao-feng, LI Yong-zhen, ZHAO Feng, et al. Feature Extraction of Precession Targets Using Multi-Aspect Observed HRRP Sequences[J]. Journal of Electronics & Information Technology, 2011, 33(12):2846-2851.
[10] 雷腾,刘进忙,杨少春,等. 基于三站一维距离像融合的弹道目标特征提取方法研究[J].宇航学报, 2012, 33(2):228-234.
LEI Teng,LIU Jin-mang,YANG Shao-chun, et al. Study on Feature Extraction Method of Ballistic Target Based on Three-Station Range Profiles[J]. Journal of Astronautic, 2012, 33(2):228-234.
[11] 王国雄. 弹头技术(上)[M]. 北京:宇航出版社, 1993.
WANG Guo-Xiong. Warhead Technology[M]. Beijing: Aerospace Publishing House,1993.
[12] 黄培康, 殷成红, 许小剑.雷达目标特性[M]. 北京:电子工业出版社, 2005.
HUANG Pei-kang, YIN Cheng-hong, XU Xiao-jian. Radar Targets Characteristics[M]. Beijing: Publishing House of Electronics Industry,2005.

