基于先验知识的最优化传感器部署方法*
刘忠义,张华睿,王妮,刘洁
(海军潜艇学院,山东 青岛 266042)
0 引言
目标检测是防空作战的关键环节。提高检测概率对提高防空拦截效率、保护己方目标等具有十分重要的意义。然而,由于低空突防战术和隐身技术的发展,防守方对攻击目标的检测正面临巨大挑战。因此,在现有传感器资源条件下,通过优化传感器部署方案,使得己方被保护目标达到最佳防护状态成为一种现实而有效的途径,开展这方面的研究也因此具有显著的实用价值。
针对传感器的最优化部署问题,现有的研究工作主要分为2部分,一是传感器威力范围对监测责任区的覆盖最优化问题[1-4],预先设定传感器在各种场景下的威力范围,然后通过优化部署方法使得多部传感器对监测责任区的覆盖比例达到最优;二是传感器对监测目标的定位精度最优化问题[5-10],通常目标的定位精度与传感器的运动轨迹或者传感器—目标的几何位置关系有关,合理规划传感器部署位置可有效提高目标定位精度。以上2部分均从不同角度对传感器最优化部署问题进行了研究,但是对于突防目标的检测却缺乏深入分析。
本文以航母编队防空作战为背景,从目标检测的角度对预警机的最优化部署问题进行了探讨。由于预警机能克服地球曲率的影响,探测范围大大优于水面舰船搭载的雷达,因此其主要担任航母编队防空警戒任务,用于检测早期突防目标[11]。在进行预警机部署时,一些先验知识和战术规则也可以作为决策依据引入到优化算法中,如突防目标的攻击意图、可能出现的攻击方位等等。本文对突防目标的作战意图进行分析,建立了目标来袭方位的模型,然后结合预警机探测性能,推导得到预警机对目标的综合检测概率,最后给出了一种以检测概率为优化函数的最优部署方法。
1 问题描述
在一个由多艘舰船组成的航母编队中,航母作为舰载机搭载平台,其拥有其他水面舰船无可比拟的重要性。航母编队若损失航母,将失去绝大部分战斗力。因此在部署预警机位置时,首要考虑因素为航母的保护[12]。航母编队的防御范围为以航母为中心、半径为R的一个圆,如图1所示。角度θ表示突防目标T进入防御圈的位置,其中正北方向为0°方位角,顺时针方向为正。根据先验知识,可预先获取突防目标在各个方位出现的概率。若舰队中部署N个预警机,其性能分别表示为:在一定虚警Pf下,预警雷达对参照目标的检测概率达到P0时,目标与雷达的距离为ri0,i=1,2,…,N。由于预警机承担的主要探测任务为突防目标的早期检测,本文将以对目标的检测概率为预警机部署方案的度量函数,即综合检测概率越高,部署方案越优,同时为了预警机的自身安全,限定其与航母的径向距离应小于预定值rmax。最终本文问题可描述为:在已知预警机探测性能的情况下,如何部署其位置S(xi,yi),i=1,2,…,N,使得其与航母的径向距离小于rmax时,对穿越防御圈的突防目标的综合检测效率达到最优。

图1 航母编队防空示意图Fig.1 Illustration of aircraft carrier formation in antiair battle
2 预警机优化部署模型
依据首要保护目标为航母的原则,以预警机对目标的综合检测概率为优化函数,逐步建立预警机的优化部署模型。本文将从预警机对目标的检测能力和目标的可能突防角度这2个方面分别展开讨论。
2.1 预警机对目标检测概率
首先考虑单个预警机部署在任意阵位(x,y)时,对进入防御圈的突防目标的检测概率。预警机的性能描述为:当虚警为Pf时,对距离为r0的参照目标的检测概率为P0。假定针对SwerlingⅠ型目标,则检测概率和信噪比满足关系式[13]
(1)
由式(1)和预警机性能可得,目标在r0处的信噪比SNR0为
(2)
同时,目标的信噪比与距离的4次方成反比,则对于距离为r的目标,其信噪比可表示为
(3)
将式(3)代入式(1),得到预警机对距离为r的目标检测概率为
(4)
其中突防目标穿越防御圈时,其与预警机的距离r可通过预警机部署位置(x,y)和目标突袭方位θ得到
(5)
基于以上推导,当同时部署N个预警机,且位置分别为xi,yi,i=1,2,…,N时,对从方位θ突防的目标的联合检测概率为
(6)
式中:PDθ,xi,yi与ri可分别由式(4)、(5)得到。
(7)
2.2 目标出现方位先验知识模型
若对敌方目标来袭方位无任何先验信息的情况下,目标可能出现方位的概率在360°上均匀分布。此时,预警机需贴近航母部署,防止目标从各个角度突防。但是,根据敌方机场相对航母编队方位、卫星图像与上级敌情通报等等,指挥官对敌方目标可能来袭方位能有大致了解。如图2a)所示。假设根据先验知识,已知在我方编队θ1和θ2方位角上,存在敌方机场或航母编队,将其分别标定为威胁1和威胁2。则突防目标可能出现方位为敌方机场和航母的对应方位,并且以θ1和θ2为出现概率值的极大值点,偏离θ1和θ2出现概率值降低。以标准正态分布为基础对目标来袭方位概率进行建模,则目标来袭方位概率密度函数为
(8)
式中:C为归一化常数;θi为第i号威胁的中心方位,Ci为其相应的权重;σi表征目标来袭方位先验知识。
当敌情不明时,目标可能出现方位不明确,σi应适当调大。若我方对敌方可能来袭方位具有较明确的先验知识,σi应适当调小。指挥官可根据实时战场态势,动态调节σi大小。Ci则根据敌方机场的远近、装备飞机的数量和先进程度确定。图2b)为目标来袭方位概率密度函数示意图。其中威胁2相对于威胁1距离我方编队更近,威胁程度更高,并且目标攻击方位更明确,所以表现为其权重C2较大,攻击方位偏差σ2较小。最终,确定各个参数分别为C1=0.6,C2=0.7,σ1=0.3°,σ2=0.2°,θ1=-20°,θ2=30°。
按照这种方法对先验知识进行建模,当敌情不明确时,仍能提取到部分有用信息,而且当情报不准确时,因为该方法采用的是概率模型,可有效避免硬性判决所带来的影响。
2.3 综合检测概率
经过上述分析,得到突防目标在各个方位出现的先验概率和预警机对其的检测概率,则由贝叶斯公式推导,当N个预警机采取某种部署方案时,其检测到穿越防御圈的突防目标的全概率为
(9)
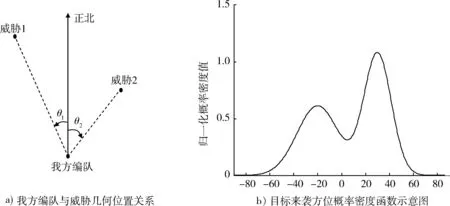
图2 目标出现方位概率Fig.2 Probability of targets’ appearance angle
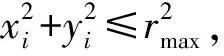
(10)
优化式(10)结合了具体的战术需求,反映了预警机在航母编队防空作战中承担的任务,并且其优化目的贴近实际应用过程。相对于以往的传感器优化部署方法,本文所提出的优化函数具有更高的应用价值。
3 基于粒子群优化的近似算法
由于预警机部署阵位优化函数非线性化程度较高,且含有积分运算,难以得到解析结果,本文将利用粒子群优化算法来解决这个问题。
粒子群优化是一种高效的近似优化算法,由Kennedy和Eberhart在1995年提出[14]。其通过模拟生物界鸟群觅食的行为特性,来搜索全局最优解。由于鸟类具有记忆能力,每一只鸟或称为粒子都会记下其运动轨迹中的最佳觅食位置(适应度函数值),定义为局部最优值p;同时,整个种群所找到的最佳位置定义为全局最优值g,该值以广播的形式告知种群中的每个粒子。粒子依据p和g调整当前的位置和飞行方向,其速度矢量分为3部分:往全局最优位置运动、往局部最优位置运动和保持原有速度,则粒子的位置更新方程为
(11)
式中:c1,c2为Hooke常数,也称为认知因子和社会因子;x,v为粒子的位置和速度矢量;下标s表示迭代次数;η1,η2为服从均匀分布u(0,1)的随机数;w为惯性加权因子。
为加快收敛速度,w通常取时变形式[15]
w=wmax-wminsmax-s/smax+wmin,
(12)
式中:wmax,wmin分别为惯性加权因子的最大值和最小值,取经验值wmax= 0.9,wmin= 0.4;smax为最大允许迭代次数。
为避免粒子收敛到局部最优解,认知加速因子c1和社会加速因子c2同样取时变形式[16]
(13)
式中:c1max,c1min,c2max,c2min分别为认知加速因子和社会加速因子的最大值和最小值,分别取经验值c1max=c2max= 2.5,c1min=c2min= 0.5。
为防止粒子跳出搜索空间[17],应根据搜索空间大小,设定最大速度限制vmax,则有||vs|| ≤vmax。
结合本文内容,以预警机的部署位置为优化变量,对突防目标的检测概率作为适应度函数,则粒子群优化算法的步骤归纳如下:
步骤1:在搜索空间内随机产生M个初始粒子位置,即预警机可能部署位置。
步骤2:判断预警机部署位置是否满足最大径向距离约束,若不是,其适应度函数设置为0;若是,计算预警机部署在该位置时对突防目标的检测概率,并将其赋予为对应的适应度函数值。
步骤3:根据各个粒子的适应度函数值更新p和g。
步骤4:依据式(11)~(13)更新粒子速度矢量和位置矢量。
步骤5:判断是否达到最大迭代次数,若满足则执行步骤6,否则执行步骤2。
步骤6:选取全局最优值对应的位置作为预警机部署的优化解,算法结束。
4 仿真实验
本文设计了2个仿真实验对文中方法的有效性进行检验。
实验1:单威胁,单预警机场景
假设航母防御圈半径为600 km,舰队部署1架预警机,其性能可表述为对距离为500 km的某型轰炸机检测概率为0.8,虚警为10-5。预警机与航母最大径向距为450 km。粒子群优化算法中,产生粒子数为10 000,粒子在每个运算周期的最大飞行距离为100 m,迭代200次,搜索空域设定为x轴(-600,600) km和y轴(-600,600) km的范围。图3给出了先验知识σ与综合检测概率P的关系图。

图3 先验知识σ与综合检测概率P变化关系Fig.3 Relationship of the priori information and detection probability
从图3可以看出,若对目标可能来袭方位有较丰富的先验知识,对应于σ较小,则对目标的检测概率会较高;概率值随着先验知识的减少而降低,以至于趋近最小极限值0.636。而按照传统方法,由于不利用对突防目标的先验知识,只能将预警机贴近航母部署,其检测概率一直维持在0.636的最低值。
实验2:双威胁,双预警机场景
假设航母防御圈半径为600 km,舰队部署2架预警机,其性能均可表述为对距离为300 km的某型轰炸机检测概率为0.8,虚警为10-5。预警机与航母最大径向距为450 km。粒子群优化算法参数设定如实验1。战场存在2个威胁,其模型参数如图 2所示。利用本文方法计算得到预警机最优部署位置为(-172.68, 398.76) km,(226.28, 388.92) km,检测概率为0.968 5。在传统方法中,一般将预警机贴近航母部署或者沿威胁轴方向上前出。按照此思路部署预警机位置为(0, 0) km,(0, 450) km,其检测概率只有0.789。可以看出,本文提出的预警机部署方法,有效地提高了对突防目标的检测概率。
若设定预警机对轰炸机的检测概率达到0.8时,以此时轰炸机与预警机的距离作为预警机的实际探测距离。当其他参数不变时,图4给出了预警机实际探测距离与综合检测概率关系图。其中实线为本文方法,虚线为传统方法。可以看出,利用本文的优化部署方法,对突入航母防御圈的目标检测概率获得较大提高。这是通过将预警机的探测能力从目标不太可能出现的方位转移到重点防护方位上,使得对目标的综合检测效率达到了最优。

图4 预警机实际探测距离与综合检测概率关系图Fig.4 Relationship of real detection range and detection probability
通过这2组实验表明,将目标的先验知识引入到预警机优化部署问题,使得预警机对目标的检测概率大幅提高,并且先验知识越丰富,检测概率越高。仿真结果符合预期设想。
5 结束语
本文以航母编队中预警机对突入防御圈的敌方目标的检测概率作为优化函数,讨论了预警机的最优部署问题。通过对目标可能出现的方位建模,在优化算法中引入已获取的突防目标的先验知识。仿真实验表明,目标的先验知识使得预警机对目标的检测概率有较大的提高。
参考文献:
[1] 王中杰, 李侠, 周启明, 等. 基于多约束条件遗传算法的雷达网优化部署[J]. 系统工程与电子技术, 2008, 30(2):265-268.
WANG Zhong-jie, LI Xia, ZHOU Qi-ming, et al. Optimal Deployment of Radar Network Based on Multi-Constrained GA[J]. Systems Engineering and Electronics, 2008, 30(2):265-268.
[2] OSMANI A, HAGHIGHT A, DEHGHAN M, et al. FSPNS: Fuzzy Sensor Placement Based on Neighbors State [C]∥Proc. of the 12th International Conference on Computer Modelling and Simulation, 2010:549-552.
[3] YI Yao, CHEN Chuang-hao, ABIDI B, et al. Can You Sen Me Now? Sensor Positioning for Automated and Persistent Surveilance[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2010, 40(1):101-115.
[4] AKHLAGHINIA R, HASHEMI S, SHADGAR B. Sensor Placement for Heterogeneous Point Coverage[C] ∥Proc. of the Second International Conference on Computer and Network Technology, 2010:13-17.
[5] YANG C, KAPLAN L, BLASCH E, et al. Optimal Placement of Heterogeneous Sensors in Target Tracking[C]∥Proc. of the 14th International Conference on Information Fusion,2011:1-8.
[6] ARANDA S, MARTINEZ S, BULLO F. On Optimal Sensor Placement and Motion Coordination for Target Tracking[R]. Santa Barbara, CA: Department of Electrical and Computer Engineering, University of California, 2004:1-9.
[7] RAJAGOPLAN R, NIU R, MOHAN C, et al. Sensor Placement for Ballistic Missile Localization Using Evolutionary Algorithms[C]∥Proc. of the IEEE International Conference on System, Man and Cybernetics,2007:284-289.
[8] CHANG Xiang-mao, TAN Rui, XING Guo-liang, et al. Sensor Placement Algorithms for Fusion-Based Surveillance Networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(8):1407-1414.
[9] BISHOP A, FIDAN B, ANDERSON B, et al. Optimality Analysis of Sensor-Target Geometries in Passive Localization: Part 1-Bearing-Only Localization[C]∥Proc. of the Third International Conference on Intelligent Sensor, Sensor Networks and Information,2007:13-18.
[10] BISHOP A, FIDAN B, ANDERSON B, et al. Optimality Analysis of Sensor-Target Geometries in Passive Localization: Part 2-Time-of-Arrival Based Localization[C]∥Proc. of the Third International Conference on Intelligent Sensor, Sensor Networks and Information, 2007:7-12.
[11] 曹毅, 苗德成, 路建伟, 等. 联合防空侦察预警系统探测能力浅析[J]. 系统工程与电子技术, 2006, 28(2):253-256.
CAO Yi, MIAO De-cheng, LU Jian-wei, et al. Analysis on Detecting Ability of the Early-Warning System for Joint Air-Defense[J]. Systems Engineering and Electronics, 2006, 28(2):253-256.
[12] 张蕾, 邓大松. 航母编队预警探测技术文集:美国海军航母编队与作战使用[R]. 南京: 中国电子科技集团公司第十四研究所, 2008:13-22.
ZHANG Lei, DENG Da-song. Collected Papers on Carrier Strike Group EW Detection Techniques: U.S. Navy Carrier Battle Group and Engagement Principle[R]. Nanjing: the 14th Research Institute of China Electronics Science Company, 2008:13-22.
[13] 卢建斌. 相控阵雷达资源优化管理的理论与方法[D]. 长沙: 国防科技大学, 2007.
LU Jian-bin. Theory and Method of Resource Optimization and Management for Phased Array Radars[D]. Changsha: National University of Defense Technology, 2007.
[14] KENNEDY J, EBERHART R. Particle Swarm Optimization [C]∥Proc. of the IEEE Conference on Neural Networks, 1995:1942-1948.
[15] SHI Y, EBERHART R. Parameter Selection in Particle Swarm Optimization[C]∥Proc. of the International Conference on Evolutionary Program, 1998:591-600.
[16] RATNAWEERA A, HALGAMUGE S K, WATSON H C. Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3):240-255.
[17] KENNEDY J. The Particle Swarm: Social Adaptation of Knowledge[C] ∥Proc. of the IEEE International Conference on Evolutionary Computation, 1997:303-308.

