复合移动床电石反应器中颗粒运动的离散单元法模拟

黄迪，曾剑桥，刘辉

（北京化工大学化工资源有效利用国家重点实验室，北京 100029）

复合移动床电石反应器中颗粒运动的离散单元法模拟

黄迪，曾剑桥，刘辉

（北京化工大学化工资源有效利用国家重点实验室，北京 100029）

针对复合移动床反应器内固体颗粒运动，采用离散单元法模型（DEM）考察布料器分别为扇形开口和矩形开口时，布料器转速和开口对颗粒运动的影响，并基于文献结果论证了本文模型的准确性。模拟结果表明：①对于不同布料器，颗粒在移动床中呈现平推流和汇聚流两种流动形态。②随布料器转速及开口的增加，颗粒质量通量非线性增加。③随布料器转速的增加，下落床径向上颗粒分布更均匀；随布料器开口的增大，下落床径向上颗粒分布范围变大，颗粒分布更均匀；对下落床径向上颗粒分布，布料器扇形开口时分布呈U形、矩形开口时分布呈M形。④沿反应器轴向向下，颗粒分布有均匀化趋势；扇形开口布料器对颗粒分布的离散系数大于1，矩形开口布料器对颗粒分布的离散系数约为0.5。

离散单元法；数值模拟；颗粒流；移动床；布料器；

颗粒床一般由大量离散的固体颗粒组成，在外力和内部应力的共同作用下运动。在颗粒物质的储存、输运、物质分离、多相反应等领域需要应用到移动床和下落床，例如鲁奇炉、BGL炉和炼铁高炉均应用移动床处理颗粒物质[1-2]，催化剂装填应用下落床分布颗粒物质[3]。近年来的一些研究[3-8]考察了在一定结构的移动床或下落床中颗粒的流动形态、停留时间分布、速度分布、出料速率等。但是将移动床和下落床结合在一个反应器（上部分为移动床，下部分为下落床）里进行考察的文章鲜见报道，而这种结合的复合床反应器对于氧热法合成电石将有重要的应用[9-10]。颗粒物质在此复合床中的运动行为对反应器的性能产生重要影响，考虑到颗粒运动的“散、动”特征，要有效地设计此复合床反应器需要对颗粒物料各种传递特性有深入认识[4]。本文采用离散单元法（discrete element method，DEM），从几何参数和操作条件两方面对影响颗粒在复合床中运动的因素进行分析，以期为新工艺中复合床的设计提供参考依据。

1 复合床流动模型

1.1 模拟对象

模拟的圆柱型复合床反应器（总高1250mm）由两部分构成：布料器以上部分为移动床，布料器以下部分为下落床；模拟的反应器整体及两种布料器如图1所示。其中，A-A截面处为布料器，沿对称方向开有下料孔。固体颗粒物料由储料室以一定初速度下落，经过布料器进行再分布，到达反应区进行反应。模拟中，由于复合床上部固体颗粒为密相，气体的动量与颗粒的动量相比可忽略不计，故不考虑气体对颗粒运动的影响；同时由于氧热法生产电石的反应物为通过预处理得到的球形颗粒，且颗粒粒径较小，具有很好的流动性能，故不考虑预处理造成部分颗粒的非球形度对颗粒流动的影响。

图1 复合床反应器及其布料器几何结构（单位：mm）

1.2 移动床模型

采用离散单元法（DEM）描述移动床内固体颗粒的运动。该法基于分子动力学原理，把不连续的颗粒离散体物料分离为刚性元素的集合，使各刚性元素满足运动方程，用时步迭代的方法求解各刚性元素的运动方程，继而得到散体的整体运动形态。颗粒的运动由牛顿第二定律和颗粒间接触的力-位移定律来描述，见式（1）、式（2）。

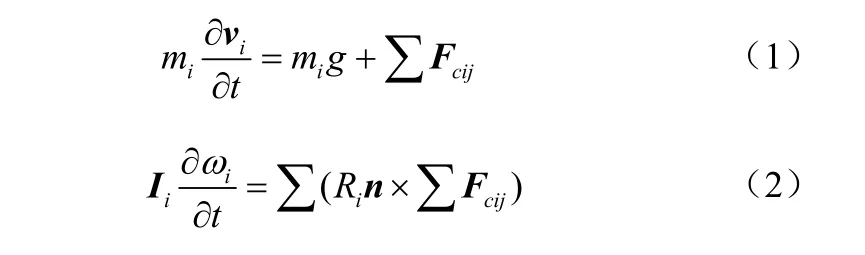
根据研究对象和目的的不同，采用的颗粒接触力模型有所不同，本文采用Hertz-Mindlin无滑动接触模型[11]。

1.3 模拟条件

自布料器向上为正方向，模拟的球形颗粒由软件EDEM2.5版本的颗粒工厂生成。储料室生成的颗粒初速度为6m/s，生成颗粒速率为每秒500粒；运行时间为0.1s时，在布料器上方静态生成2万个直径为6mm的颗粒，此颗粒群用于模拟布料器上方一定高度的移动床床层。DEM模拟中颗粒物料材质为煤，反应器材质为钢，其相关物性参数如表1所示。在表1参数相同的情况下，模拟两种布料器不同转速（转速n为5r/min、10r/min、15r/min和20r/min）与不同开口（布料器扇形开口角度θ为3.5°、5.5°和7.5°，布料器矩形开口宽度w/d为1.5、2和3）时固体颗粒在反应器中经过布料器的运动行为及颗粒与壁面的作用。

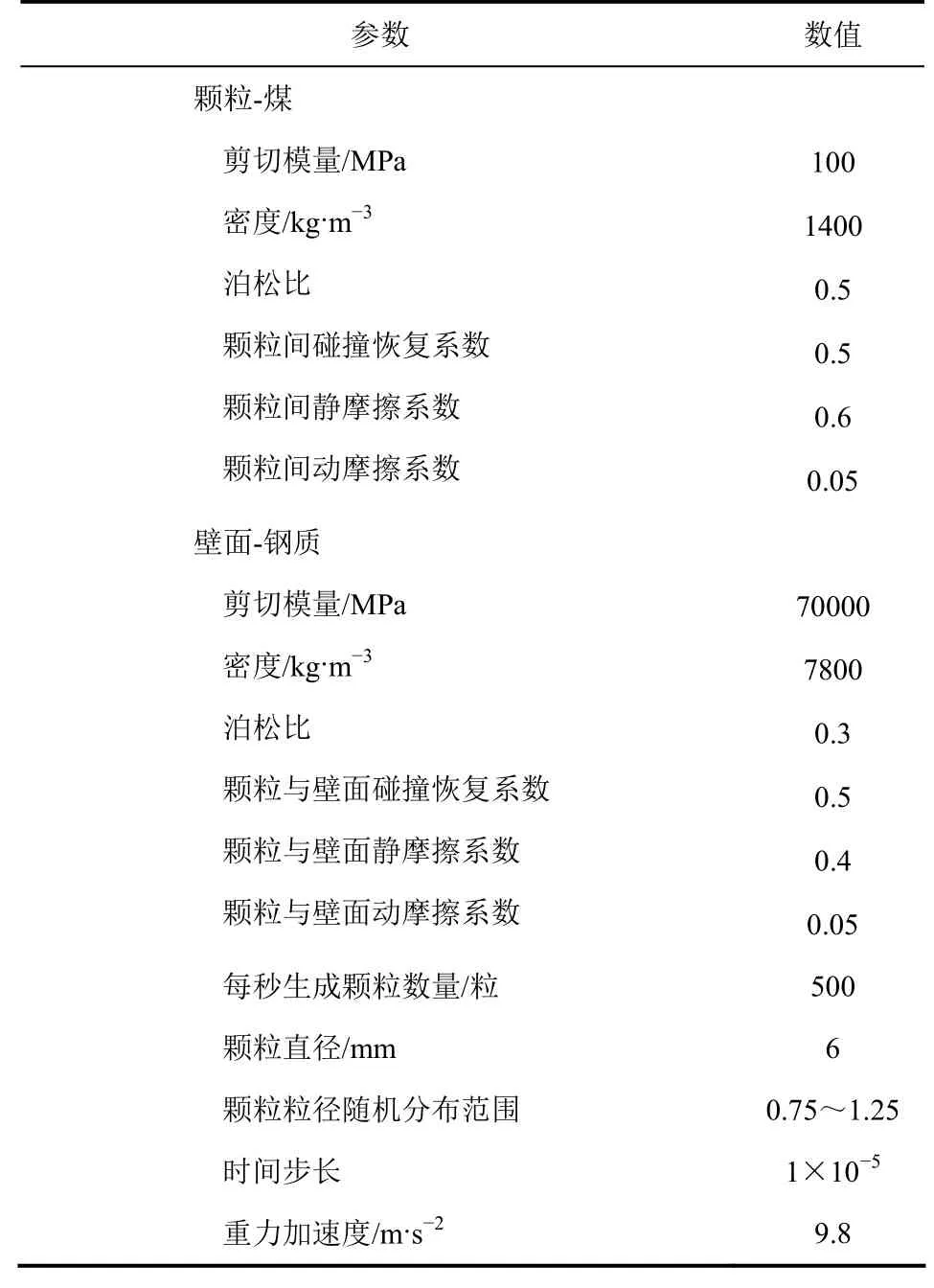
表1 DEM模拟中相关参数

1.4 模型验证

为验证本文模型建立的正确性，依据前述建立的三维颗粒运动数学模型，应用EDEM2.5版本软件，采用与Medina等[12]和赵永志等[13]的实验完全一致的反应器床型、工况、考察因素进行模拟。其中二维移动床高H=1000mm，床宽W0=300mm，床厚3.8mm，移动床右下部卸料孔宽D=20mm。

图2示出了模型验证中移动床的卸料过程，颜色深浅表示不同颗粒；其中图2(a)为赵永志等[13]在与Medina等[12]相同实验条件下计算得到的结果，图2(b)为EDEM软件模拟的结果。对比两图可见两种模拟计算结果基本一致：在0～6s只有移动床右侧颗粒排出，而左侧颗粒保持静止；6～18s内移动床顶部颗粒沿上部物料堆积斜面下滑至堆积面底部，进而排出。整个卸料过程均先排出右侧颗粒，再排出顶部颗粒，最后排出左侧颗粒。两种模拟方法吻合良好，验证了本模型方法的正确性。

图2 模拟的卸料过程

2 结果与讨论

2.1 移动床中颗粒的流动形态

为考察本文移动床内颗粒的流动形态，选取布料器转速n=15r/min、扇形开口角度θ=5.5°、矩形开口宽度与颗粒直径比w/d=2的工况，分别选定布料器上方30～40mm内颗粒，沿反应器直径方向做剖切面进行考察；图3示出了运行时间1s、5s和9s时刻的流动工况。由图3(a)可见，对于扇形开口布料器，床层中心部位，即图中两条线段之间的区域，在重力作用下颗粒层平推向下流动，属于平推流[4]（plug flow），移动床层的形状基本保持不变；在反应器其他区域内，移动床层流过一定高度后，颗粒间的相对速度差越来越大，颗粒同时存在旋转速度和垂直向下的速度，颗粒层整体向布料器开口处汇聚，颗粒的流动逐渐变为汇聚流[4]（funnel flow）；由图3(b)可见，对于矩形开口布料器，颗粒层整体先呈平推流向下运动，再呈汇聚流向开口处汇聚。在反应器中心部位均存在一定的死料区，这主要是由于布料器中心未开口造成的。

2.2 布料器转速对颗粒运动的影响

2.2.1 布料器转速对颗粒质量通量的影响

图3 颗粒在移动床反应器中的流动形态

为考察布料器旋转速度对反应器中颗粒质量通量的影响，在布料器扇形开口θ=5.5°、矩形开口w/d=2时，分别选取布料器向下-8～0mm的下落床圆柱区域，考察转速n分别为5r/min、10r/min、15r/min和20r/min共4种工况；图4示出不同转速下颗粒通过布料器后的瞬时质量通量随时间的变化。由图4可得，当运行时间一定时，颗粒在反应器中的质量通量随布料器转速的增加而增加，比较图中拟合的直线，当布料器转速成倍增加时，颗粒质量通量并未成倍增加，说明了反应器中颗粒质量通量与布料器转速不成线性关系。

比较4种转速的影响，对扇形开口布料器，如图4(a)所示，当转速为5r/min时质量通量最小，当转速为10r/min和15r/min时，图中由数据点拟合的直线值相接近，表明在此转速范围内，布料器转速对反应器中颗粒质量通量影响较小，在此转速范围内不宜通过调节布料器转速改变颗粒质量通量，当转速为20r/min时，转速对颗粒质量通量的影响较为突出；对于矩形开口布料器，如图4(b)所示，当转速较大时，下料很快，移动床段床高迅速降低，压力减小，导致在高转速时质量通量随时间有一定的下降；对比图4中的(a)、(b)两图所拟合的直线，可知颗粒质量通量随时间均有一定波动，扇形开口时波动较大，矩形开口时波动较小，这主要是由颗粒的离散性及布料器的旋转导致的。

图4 布料器不同转速时颗粒质量通量随时间的变化

2.2.2 布料器转速对颗粒通过布料器后分布的影响

为考察布料器旋转速度对颗粒通过布料器后径向分布的影响，在布料器扇形开口θ=5.5°、矩形开口w/d=2、运行时间t=9.5s时，取布料器向下z=-150mm处沿直径分布的14个小长方体，考察转速n分别为5r/min、10r/min、15r/min和20r/min共4种工况；图5示出不同转速下颗粒通过布料器后沿反应器径向的分布情况。对比图5中的(a)、(b)两图，扇形开口布料器时颗粒分布呈U形，矩形开口布料器时颗粒分布呈M形，这是由于布料器中间及边壁未开口导致的。当转速为5r/min时，颗粒在下落床内分布与其他3个转速相比波动较大，这主要是由于转速较小时，布料器旋转对颗粒架桥现象的破坏作用较小，颗粒间力链结构不稳定，导致下料量及分布不稳定。比较4种转速可见随转速增加，下料量增加，颗粒沿反应器径向分布也更均匀。

2.3 布料器开口对颗粒运动的影响

2.3.1 布料器开口对颗粒质量通量的影响

图5 布料器转速对颗粒沿反应器径向分布的影响

对布料器，不同的开口对应不同的开孔率，为考察布料器开口对反应器中颗粒质量通量的影响，在布料器转速n=15r/min时，选取布料器向下-8～0mm的下落床圆柱区域，分别考察扇形开口角度θ为3.5°、5.5°和7.5°，矩形开口w/d为1.5、2和3共6种工况；图6示出布料器不同开口时颗粒通过布料器后的瞬时质量通量随时间的变化。

对比图6中的(a)、(b)两图中不同工况下拟合的直线，可得随着开口的增大，颗粒质量通量迅速增加，这是由于开口较小时，颗粒容易形成架桥现象，不易下落，随开口角度增大，颗粒的架桥现象减弱，且布料器的旋转也对颗粒间架桥现象起到一定的破坏作用。对于扇形开口，在颗粒粒径一定时，随着布料器开口角度的增加，布料器能通过颗粒的范围迅速增大，开口角度较小时，布料器径向上由中心开始向外有相当大的范围内不能通过颗粒。对于矩形开口布料器，随着开口宽度的增加，下料量也迅速增加，当布料器开口宽度成倍增加时，颗粒质量通量并未成倍增加，说明了反应器中颗粒质量通量与布料器开口宽度不成线性关系。由图6可知，颗粒质量通量随时间有一定波动，扇形开口时波动较大，矩形开口时波动较小，这主要是由颗粒的离散性及布料器的旋转导致的。

图6 布料器不同开口时颗粒质量通量随时间的变化

2.3.2 布料器开口对颗粒通过布料器后分布的影响

为考察布料器开口对颗粒通过布料器后径向分布的影响，在布料器转速n=15r/min、运行时间t=9.5s时，取布料器向下z=-150mm处沿直径分布的14个小长方体，分别考察扇形开口角度θ为3.5°、5.5°和7.5°，矩形开口w/d为1.5、2和3共6种工况；图7示出不同开口时颗粒通过布料器后沿反应器径向的分布情况。

由于布料器的旋转带动颗粒旋转，给予颗粒径向运动的动量，使颗粒通过布料器后能向反应器中心方向运动。对比图7中的(a)、(b)两图，对于扇形开口布料器，颗粒分布呈U形，随着开口角度的增加，颗粒下落质量和颗粒在反应器径向上的分布范围都增加，且分布范围均大于该开口角度条件下布料器可通过颗粒的最大范围；而对于矩形开口布料器，颗粒分布呈M形，且随着开口宽度的增加，M形越突出，即此时颗粒分布越不均匀。

2.4 颗粒经过布料器后在不同轴向位置的分布比较

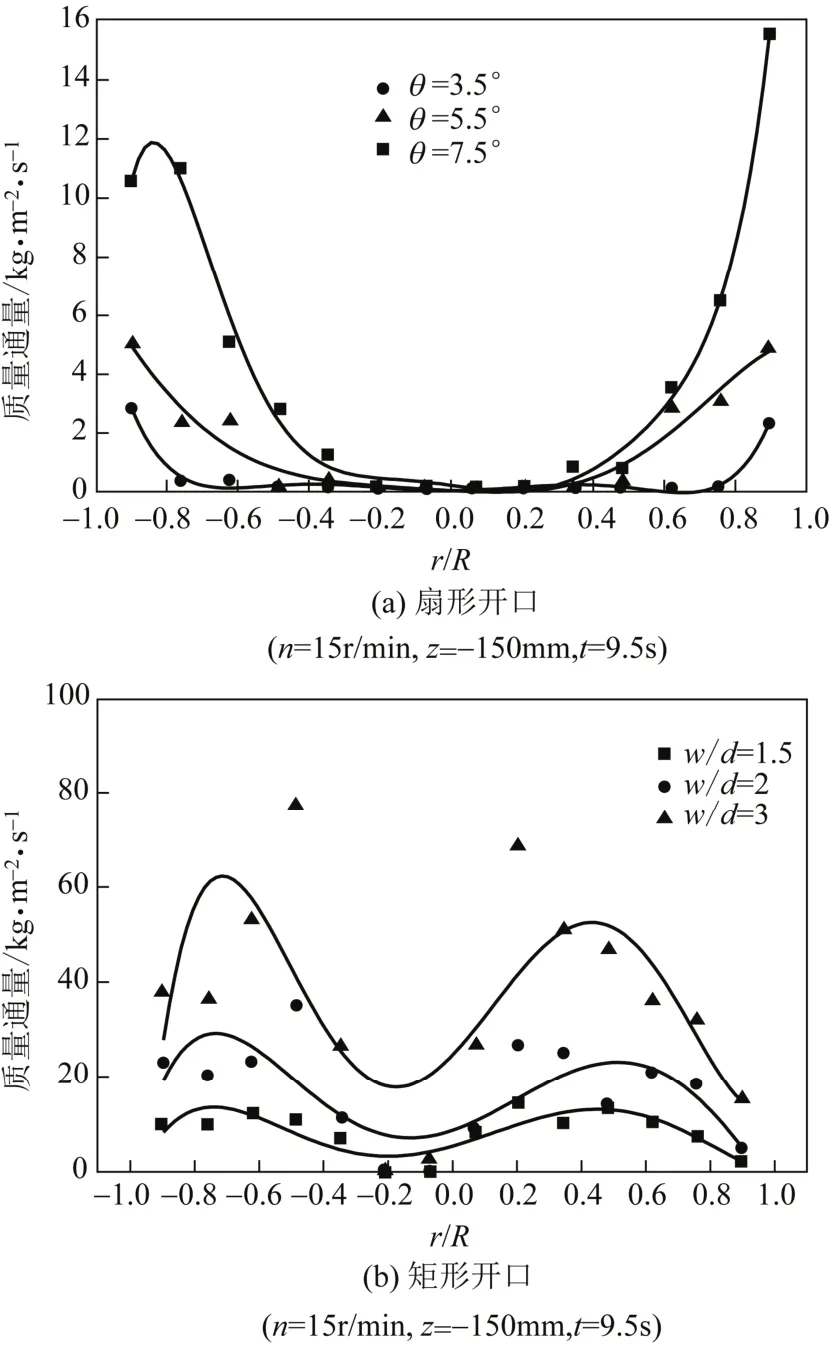
图7 布料器开口对颗粒沿反应器径向分布的影响

在布料器转速n=15r/min，扇形开口θ=5.5°、矩形开口w/d=2，运行时间t=9.5s时，在布料器下方-50mm、-150mm、-250mm、-350mm处分别取高8mm的下落床圆柱，在此圆柱区域内沿反应器直径x方向依次取14个长20mm、宽20mm、高8mm的小长方体，分别考察两种布料器时颗粒在下落床段的分布。

图8示出颗粒经过布料器后，沿反应器轴向分布的情况，图中原点是反应器在该轴向位置的中心。由于布料器中心未开口，下落床中心区域的颗粒来自于布料器的旋转带动颗粒旋转，给予颗粒径向运动的动量，使颗粒通过布料器后能向反应器中心方向运动。由图8(a)可见，对扇形开口布料器，颗粒分布呈U形，从布料器开始沿反应器轴向向下，颗粒分布越来越均匀，在反应器半径|r/R|＜0.3 的区域内始终没有颗粒的分布；由图8(b)可见，对矩形开口布料器，颗粒分布呈M形，从布料器开始沿反应器轴向向下M形减弱，颗粒分布越来越均匀。

对于不同布料器，根据不同轴向位置颗粒的分布情况，可以指导对于电石合成复合床反应器，在距离布料器一定轴向高度时喷氧燃烧焦炭供热的火焰的径向位置，对于反应器中心没有颗粒分布的情况，喷氧嘴不宜设置在反应器中心位置[14]。

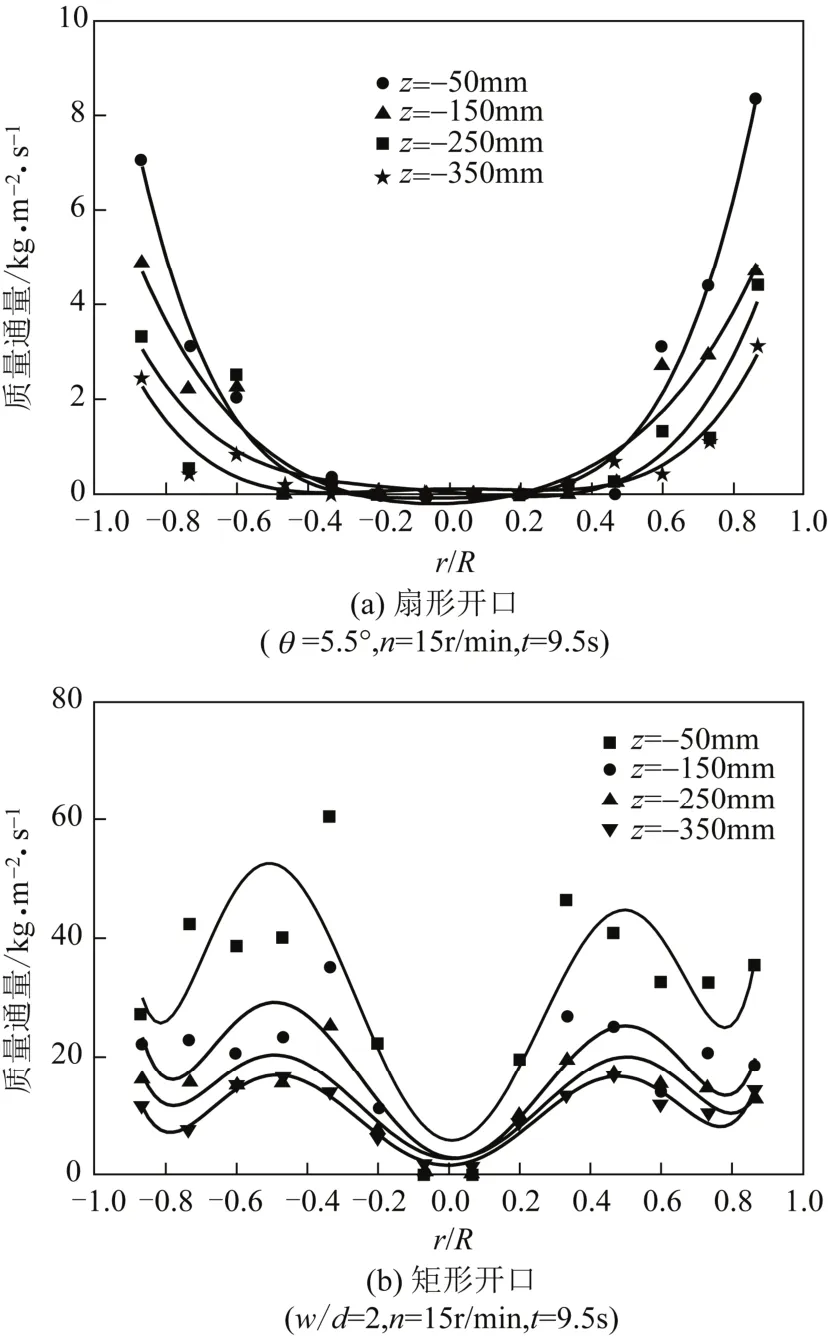
图8 颗粒经过布料器后不同轴向位置的分布

图9所示为不同工况下的离散系数（coefficient of variance，Cv）的比较，由图9可见，对于扇形开口布料器，各种工况下离散系数均大于1，这是因为布料器扇形开口，布料器中心一定范围内不能通过颗粒，导致颗粒通过布料器后在下落床内的分布很不均匀。当开口角度为3.5°时，离散系数随转速变化很大，且数据点偏离线性大，这是由于开口较小时颗粒间易形成架桥现象，布料器运动对布料器上方颗粒的力链结构产生作用，破坏颗粒间的架桥现象，不同转速时的破坏程度不同；当开口角度为5.5°和7.5°时，离散系数随转速变化小，且数据点偏离线性小，表明开口角度较小时，转速对颗粒通过布料器后的分布影响较大。而对于矩形开口布料器，离散系数约为0.5，且数据点偏离线性小，即对于此复合床反应器，矩形开口时颗粒在下落床段的分布更均匀、更稳定。

3 结 论

本文以复合移动床中颗粒运动为研究对象，采用离散单元法，运用EDEM软件对其中颗粒流动进行模拟，考察了对于反应器中扇形开口和矩形开口两种布料器，操作参数和几何条件对颗粒在床中运动及分布的影响，得到如下结论。

图9 不同工况下离散系数的比较（z=-150mm，t=9.5s）

（1）基于二维移动床中软件模拟与实验结果一致，验证了所采用模型方法的正确性。

（2）颗粒在移动床中运动有两种形态：布料器扇形开口时，中间部位床层整体呈平推流，其他部位床层先呈现平推流，再呈现汇聚流；布料器矩形开口时颗粒整体先呈现平推流，再呈现汇聚流。

（3）随布料器转速增加，颗粒质量通量增加；颗粒在反应器径向上分布随转速增加而更均匀，对不同转速，布料器扇形开口时分布呈U形、矩形开口时分布呈M形。

（4）随着布料器开口大小的增加，颗粒质量通量增加；颗粒在反应器径向上的分布随开口大小的增加而更均匀，对于不同开口，布料器扇形开口时分布呈U形、矩形开口时分布呈M形。

（5）沿反应器轴向向下，颗粒分布越来越均匀；布料器扇形开口时，颗粒分布的离散系数均大于1，矩形开口时，颗粒分布的离散系数均约为0.5，矩形开口布料器对均匀分布颗粒更有利。

符 号 说 明

d——颗粒直径，mm

E*——有效弹性模量，Pa

F——颗粒间应力，N

Fc——颗粒间的接触力，N

Fd——颗粒间的阻尼力，N

g——重力加速度，m/s

I——转动惯量，kg·m2

L——布料器矩形开口长度，mm

m——颗粒质量，kg

m*——等效质量，kg

n——布料器转速，r/min

n——发生碰撞时法向单位矢量

R——布料器半径，mm

Ri——颗粒i的半径，mm

R*——等粒子半径，mm

r——布料器上一点到布料器中心的距离，mm

S——刚度，Pa·m

t——时间，s

v——颗粒速度，m/s

vrel——颗粒间相对速度，m/s

w——布料器矩形开口宽度，mm

α——两球形颗粒发生弹性接触时的法向重叠量，mm

δ——两球形颗粒发生弹性接触时的切向重叠量，mm

θ——布料器扇形开口角度，(°)

ω——颗粒运动角速度，rad/s

下角标

ij——颗粒i与颗粒j之间

i，j——颗粒i（j）

n——法向方向

t——切向方向

[1] Yoon H，Wei J，Denn M. A model for moving bed coal gasification reactors[J].AIChE. J.，1978，24（5）：885-903.

[2] 汪家铭. BGL碎煤熔渣气化技术及其工业应用[J]. 化学工业，2011，29（7）：34-39.

[3] 潘兵，刘雪东，刘文明，等. 基于离散元法的催化剂密相装填过程数值模拟[J]. 中国粉体技术，2011，17（6）：32-37.

[4] 武锦涛，陈纪荣，阳永荣. 移动床中颗粒运动的数值模拟[J]. 石油化工，2005，34：814-816.

[5] Chen Jizhong，Akiyama Tomohiro，Nogami Hiroshi，et al. Modeling of solid flow in moving beds[J].ISIJ International，1993，33（6）：664-671.

[6]Cundall P A，Strack O D L. A discrete numerical model for granular assemblies[J].Geotechnique，1979，29（1）：47-65.

[7] Radjai Farhang，Jean Michel，Moreau Jean-Jacques，et a1. Force distributions in dense two-dimensional granular systems[J].Phys. Rev. Lett.，1996，77（2）：274-277.

[8] 武锦涛，陈纪忠，阳永荣. 模拟颗粒流动的离散元方法及其应用[J]．现代化工，2003，23（3）：56-58.

[9] 刘振宇，刘清雅，李国栋，等. 一种电石生产方法：中国，101327928A[P]. 2008-12-24.

[10] 刘振宇，刘清雅，李国栋. 一种电石生产系统：中国，101428799A[P]. 2009-05-13.

[11]王国强，郝万军，王继新. 离散单元法及其在EDEM上的实践[M].西安：西北工业大学出版社，2011.

[12] Medina A，Andrade J，Cordova J A，et a1. Gravity induced granular flow measurements in a 2D silo with a lateral bottom exit[J].Physics Letters A，2000，273：109-116.

[13] 赵永志，程易，金涌. 颗粒移动床内不稳定运动的计算-颗粒动力学模拟[J]. 化工学报，2007，58（9）：2216-2224.

[14] 于洋，李文涛，刘辉，等. 氧热法电石生产气流床反应器性能的数值模拟[J]. 北京化工大学学报，2013，40（3）：27-31.

Discrete element method simulation of particle flow in a combined-moving bed reactor for carbide production

HUANG Di，ZENG Jianqiao，LIU Hui
（State Key Laboratory of Chemical Resource Engineering，College of Chemical Engineering，Beijing University of Chemical Technology，Beijing 100029，China）

In this paper，the particle flow in a combined-moving bed reactor was simulated using the discrete element method（DEM），and the accuracy of DEM simulation was verified by a comparison with the literature results. The effects of rotational speed and open-hole size of two kinds of distributing devices were analyzed. The results showed that：①There are two kinds of flow patterns for the two distributing devices，i.e.，plug flow and funnel flow；②particle mass fluxes increased non-linearly with the increase of rotational speed and open-hole size of the distributing devices；③along the radial direction，particles were distributed more uniformly with increasing the rotational speed and open-hole size，and the distribution showed U and M shapes for the two kinds of distributing devices；④the radial distribution of particles were more uniformly downwardly along the axial direction，with values of the variance coefficient exceeding 1.0 for the fan-shaped hole distributing plate，and 0.5 for another distributing plate.

discrete element method；numerical simulation；granular flow；moving bed；distributing device

TQ 018

A

1000-6613（2014）10-2576-07

10.3969/j.issn.1000-6613.2014.10.010

2014-03-12；修改稿日期：2014-03-28。

国家973计划项目（2011CB201306）。

黄迪（1987—），男，硕士研究生。联系人：刘辉，教授，博士生导师。E-mail hliu@mail.buct.edu.cn。