基于最小二乘支持向量机的蜡沉积速率预测

靳文博，敬加强，田震，孙娜娜，伍鸿飞

（西南石油大学油气消防四川省重点实验室，四川 成都 610500）

基于最小二乘支持向量机的蜡沉积速率预测

靳文博，敬加强，田震，孙娜娜，伍鸿飞

（西南石油大学油气消防四川省重点实验室，四川 成都 610500）

考虑蜡沉积影响因素的复杂性和最小二乘支持向量机在小样本预测方面的优势，基于最小二乘支持向量机预测的原理，通过优化最小二乘支持向量机的参数，建立了蜡沉积速率的预测模型，并对蜡沉积速率进行了预测。结果表明：该方法在样本数量较小时仍具有较高的精度，蜡沉积速率的预测值和实验值的吻合程度较好；最小二乘支持向量机建模时可以得到直观的函数表达式，而神经网络方法却不能得到模型的显式表达式，因此该方法具有明显的优势；应用径向基核（RBF）作为核函数时，不同初值的正则化参数γ和核函数宽度σ对预测结果具有较大影响，使用时应合理选择。

最小二乘支持向量机；蜡沉积速率；预测；模型；模型精度

易凝高黏含蜡原油一般采用加热输送工艺，其目的主要是降低原油的黏度和改善原油的流动性，减少摩阻损失。在加热输送的过程中，由于环境温度低于管内的原油温度，因此原油的温度将不断降低，当其达到原油的析蜡点时，蜡分子析出，部分蜡分子会沉积到管壁上形成结蜡层。蜡沉积使得管道的有效流通面积减少，流动阻力增大，给管道的安全经济运行带来了很多困难[1-3]。

国内外学者对于蜡沉积的研究已开展了很多年，目前环道实验装置使用的较多，这为蜡沉积规律的认识及蜡沉积模型的建立提供了大量的实验数据[4-6]。众所周知，影响蜡沉积速率的因素多而复杂，不同的影响因素间又相互影响，这给蜡沉积的研究带来了诸多困难。为了进一步掌握各因素对蜡沉积速率的影响规律，一般要安排大量的实验才能确定。但是，蜡沉积实验一般要耗费大量的时间和人力，这使得研究者所得的蜡沉积实验数据一般比较有限。因此，如何利用所得的实验数据建立可靠的预测方法和模型就显得尤为重要。周诗岽等[7]采用逐步回归分析法和人工神经网络法预测了蜡沉积速率，结果表明人工神经网络法的精度较高。逐步回归分析法只能描述线性关系，但计算速度快且能反映蜡沉积速率与影响因素之间的亲疏关系；人工神经网络法则可以描述多因素之间的非线性关系，但计算速度慢且不能得到蜡沉积速率模型的显式表达式。从德胜等[8]利用L-M优化方法来求解模型中的回归参数，通过算例证实了此方法得到的模型精度高于逐步回归分析法。

管输含蜡原油蜡沉积速率的影响因素较多，各因素间往往存在着一个复杂的非线性关系，故管道的蜡沉积速率预测应是一个多因素的非线性预测问题。神经网络具有很强的非线性映射能力和强大的自学习能力，可映射任意复杂的非线性关系。但是神经网络受网络结构的复杂性和样本复杂性的影响较大，且有时会出现过学习、训练时间长、低泛化能力以及易陷入局部极小值等问题[9]。支持向量机（support vector machine，SVM） 是近年来发展起来的一种新型学习机器，是统计学习理论的一种通用学习方法。它通过结构风险最小化原理来提高泛化能力，能较好地解决小样本、非线性、高维数及局部极小点等实际问题[10-11]。而最小二乘支持向量机（LS-SVM）是支持向量机的一种扩展，该方法采用最小二乘线性系统作为损失函数，用等式约束替代不等式约束，使得求解过程变成了解一组等式方程，从而降低了模型的复杂程度，提高了求解速度[12]。基于此，本文将最小二乘支持向量机的思想引入到蜡沉积速率的预测中，通过优化最小二乘支持向量机的参数，预测了管道的蜡沉积速率，建立了蜡沉积速率的预测模型，这对于蜡沉积规律的研究具有一定的指导意义。

1 最小二乘支持向量机的原理

最小二乘支持向量机是支持向量机的一种改进，它将传统支持向量机中的不等式约束改为等式约束，并将解二次规划问题转化为求解线性方程组问题，其基本原理如下：对于一个训练样本集其中xi为输入数据，yi为输出数据。用一非线性映射φ(·)把样本从原空间Rn映射到特征空间φ(xi)，这样可使得非线性回归问题变成高维特征空间的线性回归问题，在这个高维特征空间中构造最优决策函数，如式（1）。

基于结构风险最小化原理，此回归问题可以表示为约束优化问题，如式（2）。

式中，γ为正则化参数；ω为权向量；ei为误差变量；b为偏差量。对于式（2）引入拉格朗日函数，得式（3）。

式中，αi为lagrange乘子（支持向量），对式（3）优化后可得式（4）。

对式（4）可进一步消除变量ω、e，得如下式（5）矩阵方程。

式中，α与b可应用最小二乘法从方程式（5）中求得。

2 最小二乘支持向量机预测蜡沉积速率的步骤

Matlab的最小二乘支持向量机工具箱为蜡沉积速率的预测提供了便利，预测的步骤如下。①建立学习样本和测试样本：基于蜡沉积环道实验数据[13]，以管壁处的剪切应力（τ）、管壁处温度梯度（T'）、管壁处蜡分子浓度梯度（C'）、原油的动力黏度（μ）、流速（υ）、壁温（TB）以及油温（TY）这7个影响因素作为输入向量，以蜡沉积速率（Wr）作为输出向量。数据共计38组，取其中的20组作为学习样本，其余样本为测试样本。②数据的导入和预处理：对读入的数据进行预处理，预处理的目的主要是可以加快训练速度。所用的函数为Prestd归一化函数。③核函数的选择：核函数有不同的形式，常用的有线性核、多项式核、径向基核（RBF）等，RBF核只有一个待定参数，拟合精度较高，文中选取RBF核。④参数的选取：对于采用RBF核的最小二乘支持向量机，其主要参数是选取正则化参数γ和核函数宽度σ，即寻找最优的γ和σ组合，使得LS-SVM具有良好的预测能力。文中应用Matlab工具箱中的Tunelssvm函数通过交叉验证寻优的方法得到最佳的参数组合。⑤训练建立模型：利用最小二乘支持向量机对学习样本进行样本学习，得到输入参数和输出参数的关系。利用Trainlssvm函数来训练建立模型，训练结束后即可得到支持向量和偏差量。⑥测试样本预测：导入预测数据，预处理后利用Simlssvm函数对测试样本进行预测，并分析其预测的精度。

3 蜡沉积速率预测结果

利用文献[13]的38组蜡沉积环道实验数据，取其中的20组作为学习样本，其余的18组为测试样本来进行预测。测试样本的数据如表1所示。

从表1可见，蜡沉积速率的影响因素错综复杂，数据毫无任何规律，因此在多个影响因素下（7个）建立蜡沉积速率的模型难度较大。此处利用最小二乘支持向量机，依据上述预测步骤，预测了测试样本的蜡沉积速率值，结果如图1所示。

预测得到的相关系数为0.9832，故该方法的预测精度高。偏差量b为5.1577，得到最优的参数组合为：[γ，σ]=[2756.55，208.44]。从图1中蜡沉积速率的实验值与预测值的结果可见，预测值和实验值的吻合程度较好，因此采用最小二乘支持向量机来预测蜡沉积速率是可行的。

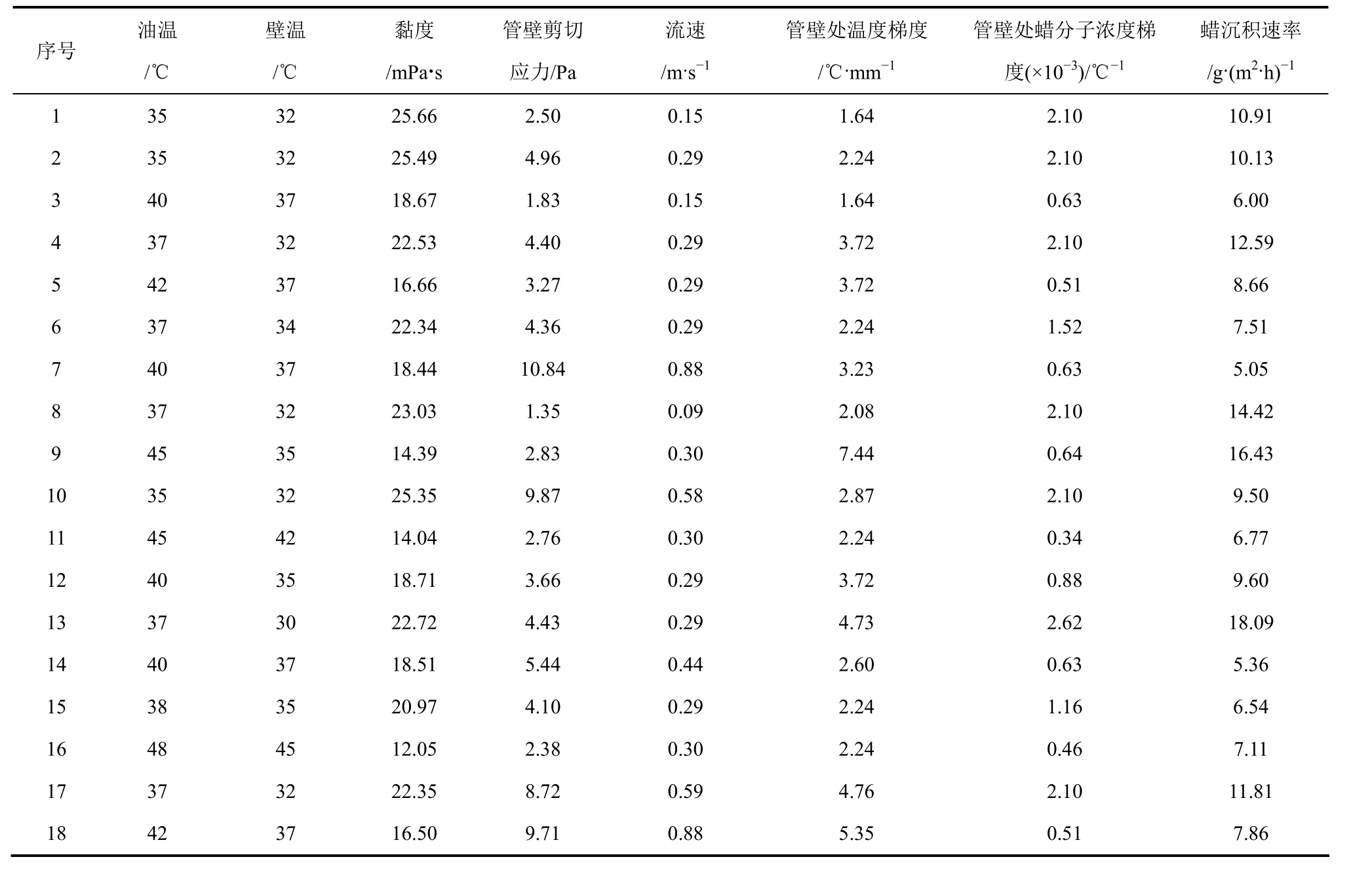
表1 测试样本

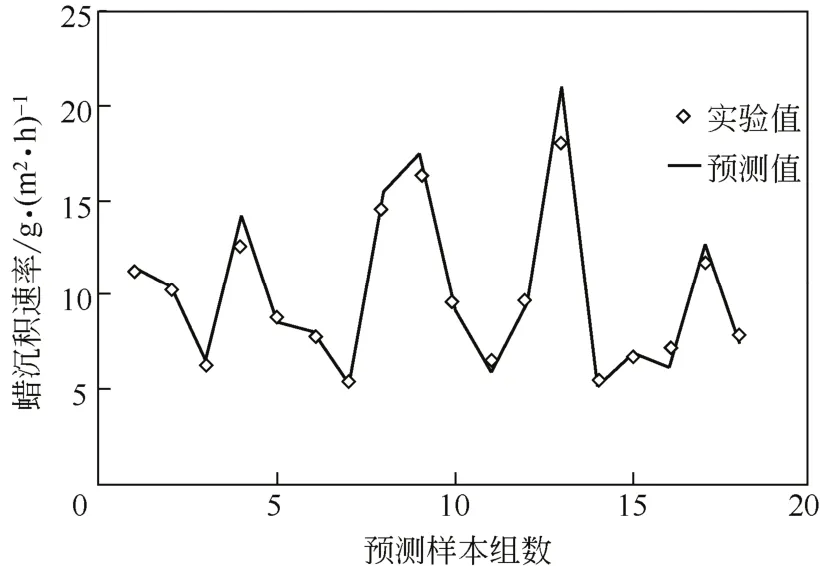
图1 最小二乘支持向量机预测结果

4 最小二乘支持向量机建立蜡沉积速率模型

通过对蜡沉积速率实验数据的回归，可以得出蜡沉积速率与各影响因素间的对应关系，由此可以得出蜡沉积速率的预测模型。

由前述最小二乘支持向量机的原理中式（6）可得到蜡沉积速率的预测式为式（7）。

所得的支持向量αi如表2所示，将其带入式（7）中即可得到20组学习样本训练后的蜡沉积速率预测模型。从该模型可以看出，最小二乘支持向量机在确定核函数的形式和相应的参数后，就可以得到预测蜡沉积速率的直观函数表达式。从训练的结果来看，最小二乘支持向量机每次训练时得到的解析式是唯一的，这也是最小二乘支持向量机的一个优势。

表2 支持向量

5 最小二乘支持向量机的参数对预测性能的影响

对于采用RBF作为核函数的最小二乘支持向量机而言，其主要考虑的是参数γ和σ，这两个参数在很大程度上决定了最小二乘支持向量机的学习能力和泛化能力。文中在预测的过程中，发现这两个参数取不同的初值对模型的预测结果具有较大的影响。此处取γ=500，σ=10，以相关系数为评定标准，通过改变γ和σ的取值来分析这两个参数对预测结果的影响。首先固定γ，变化σ，取其多次预测结果相关系数的平均值来分析σ对预测结果的影响；之后固定σ，变化γ，探讨γ对预测结果的影响，所得的结果如图2和图3所示。

从图2可见，σ值的改变对于预测结果的影响很大。随着σ值的增加，预测的精度提高。当σ值为10时，预测的精度高且相关系数变化较小（多次的预测结果），因此此时的σ值适合用于最小二乘支持向量机的预测。从图3可见，当σ值为10时，预测的精度均较高。随着γ值的增加，预测的精度有所提高。当γ为100时，预测的精度可达到很高的程度。

图2γ=500时相关系数随σ值的变化趋势

图3σ=10时相关系数随γ值的变化趋势

6 结 论

（1）基于室内蜡沉积环道实验数据，考虑了7个影响管输含蜡原油蜡沉积速率的因素，并将最小二乘支持向量机的原理引入到蜡沉积速率的预测中。结果表明蜡沉积速率的实验值和预测值之间的吻合程度较好，因此最小二乘支持向量机可用来预测蜡沉积速率。

（2）利用最小二乘支持向量机，建立了管壁处的剪切应力、管壁处温度梯度、管壁处蜡分子浓度梯度、原油的动力黏度、流速、壁温以及油温这7个影响因素与蜡沉积速率之间的预测模型。该方法与神经网络法相比，可得到蜡沉积速率模型的直观函数表达式；该方法与逐步回归分析法相比，逐步回归分析法只能描述线性关系，因此在此方面最小二乘支持向量机具有明显的优势。

（3）当采用RBF作为最小二乘支持向量机的核函数时，不同初值的正则化参数γ和核函数宽度σ对于预测结果的影响较大，因此具体应用时应合理选择最小二乘支持向量机的参数，以便使其达到很好的预测效果。

[1] Huang Z Y，Lu Y D，Hoffmann R，et al. The effect of operating temperatures on wax deposition[J].Energy Fuels，2011，25：5180-5188.

[2] 孙百超，王岳，尤国武. 含蜡原油热输管道管壁结蜡厚度的计算[J]. 石油化工高等学校学报，2003，16（4）：48-51.

[3] Hoteit H，Banki R，Firoozabadi A. Wax deposition and aging in flowlines from irreversible thermodynamics[J].Energy Fuels，2008，22（4）：2693-2706.

[4] 王霞光，蔡均猛. 模型环道的蜡沉积实验[J]. 石油化工高等学校学报，2005，18（2）：64-66.

[5] Bidmus H O，Mehrotra A K. Solids deposition during “Cold Flow” of wax-solvent mixtures in a flow-loop apparatus with heat transfer[J].Energy Fuels，2009，23：3184-3194.

[6] 黄启玉，张劲军，高学峰，等. 大庆原油蜡沉积规律研究[J]. 石油学报，2006，27（4）：125-129.

[7] 周诗岽，吴明. 管道输送原油蜡沉积速率模型研究[J]. 辽宁石油化工大学学报，2004，24（2）：73-77.

[8] 从德胜，汪玉春. L-M方法优化管输原油蜡沉积速率模型[J]. 油气储运，2009，28（5）：19-21.

[9] 朱家元，张喜斌，张恒喜，等. 多参数装备费用的支持向量机预测[J]. 系统工程与电子技术，2003，25（6）：701-703.

[10] Vapnik V N. An overview of statistical learning theory[J].IEEE Trans Neural Network，1999，10（5）：988-999.

[11] 张全明，刘会金. 最小二乘支持向量机在电能质量扰动分类中的应用[J]. 中国电机工程学报，2008，28（1）：106-110.

[12] 郭辉，刘贺平，王玲. 最小二乘支持向量机参数选择方法及其应用研究[J]. 系统仿真学报，2006，18（7）：2033-2036.

[13] 王雪亮. 华池作业区管输原油蜡沉积现象预测分析研究[D]. 西安：西安石油大学，2010.

Prediction of wax deposition rate based on least squares support vector machine

JIN Wenbo，JING Jiaqiang，TIAN Zhen，SUN Nana，WU Hongfei
（Oil and Gas Fire Protection Key Laboratory of Sichuan Province，Southwest Petroleum University，Chengdu 610500，Sichuan，China）

Considering the complexity of the influence factors of wax deposition and the advantage of least squares support vector machine in small sample prediction，based on the prediction principles of least squares support vector machine，by optimizing the parameters of least squares support vector machine，the prediction model of wax deposition rate was established and wax deposition rate was predicted. The method had higher accuracy when the samples were fewer，and the prediction results of wax deposition rate was in good agreement with the experimental data. The least squares support vector machine could get the intuitive function expression when it was used to establish the model of wax deposition rate，while neural network method could not get explicit expression. so this method has sufficient preponderance. When the RBF kernel function was used，different initial values of regularization parametersγand kernel bandwidthσhad a greater impact on the predicted results，so it should be used with care.

least squares support vector machine；wax deposition rate；prediction；model；model accuracy

TE83

A

1000-6613（2014）10-2565-05

10.3969/j.issn.1000-6613.2014.10.008

2014-02-17；修改稿日期：2014-04-08。

靳文博（1986—），男，博士研究生，主要从事油气集输技术与理论研究。E-mail jinwenbo725@163.com。联系人：敬加强，教授，博士生导师。E-mail believemetoo@sina.com。