扇图与轮图的边平均Wiener指标及其算法

赵相佩，李月清，叶永升，黄杜娟

（1.淮北师范大学 数学科学学院，安徽 淮北 235000；2.北京工业职业技术学院 基础教育学院，北京 100042；3.淮北师范大学 计算机科学与技术学院，安徽 淮北 235000 ）

1 预备知识

本文考虑的图都是有限无向简单图.设G=(V(G),E(G))是一个图，分别用V(G),E(G)表示图G的顶点集和边集，|V(G)|,|E(G)|表示顶点数和边数，dG(u)表示顶点u在G中的度数，dG(x,y)表示两顶点x和y之间的距离，Diam(G)表示图G的直径.图G的Wiener指标在图G中，两边f=uv的顶点和g=xy的顶点间最短路的长度称为f=uv和g=xy的距离，记DG(f,g)，即：DG(f,g)=min{dG(u,x),dG(u,y),dG(v,x),dG(v,y)}.据此，即可给出图G的边Wiener 指标的定义在连通图G中，DG′(f,g)表示任意两条边f=uv和g=xy之间平均距离，即

文献［3］首次引进图G的边平均Wiener指标

文献［4-6］已研究了n阶单圈图、n阶连通图及有m条边连通图的边平均Wiener指标.本文将研究并给出扇图中任意两边之间的平均距离的算法程序.

2 n阶扇图Fn的边平均Wiener指标

定义1［7］设Pn-1是有n-1个顶点的路，P1与Pn-1的联图P1∨Pn-1称为扇图Fn.设

记vivi+1=ei(i=1,2,…,n-2),v0vj=en-2+j(j=1,2,…,n-1)(如图1所示).

由图的边平均Wiener指标的定义可知，一个图的边平均Wiener指标就是这个图的任意两边之间的平均距离之和.为了计算扇图的边平均Wiener 指标，我们把扇图的边分为两类，即{e1,e2,…,en-2}和{en-1,en,…,e2n-3}.下面分三种情形讨论.

情形1：任取ei,ej∈{e1,e2,…,en-2}时，

图1 扇图 Fn

情形2：任取ei∈{e1,e2,…,en-2}，ej∈{en-1,en,…,e2n-3}时，

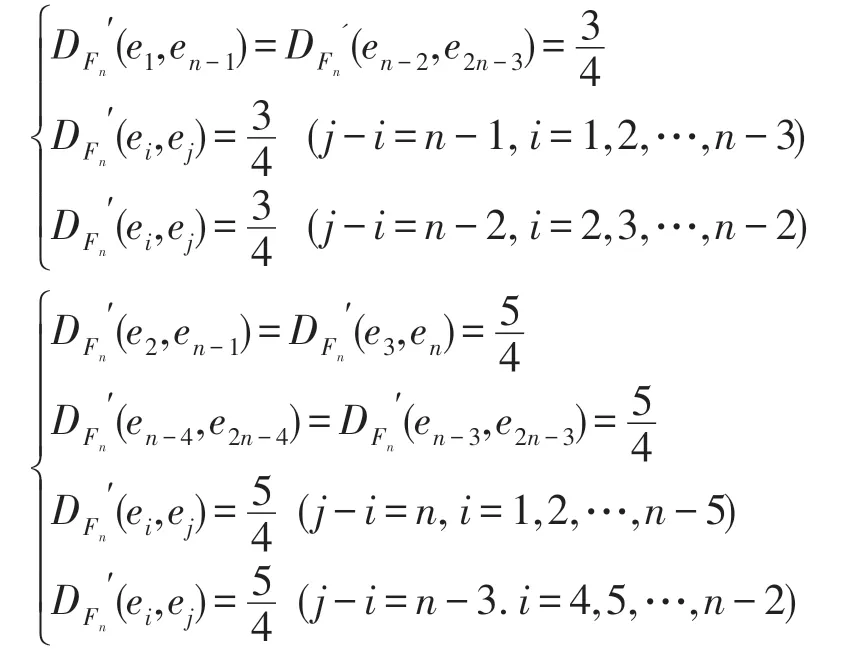
情形3：任取ei,ej∈{en-1,en,…,e2n-3}时

容易验证，F3的边平均Wiener 指标当n很大时，需要计算对边的平均距离，由此可见计算量是很大的，手工计算起来非常繁琐且易出错.我们用Microsoft Visual C++6.0计算扇图中任意两边之间的平均距离，核心程序如下：

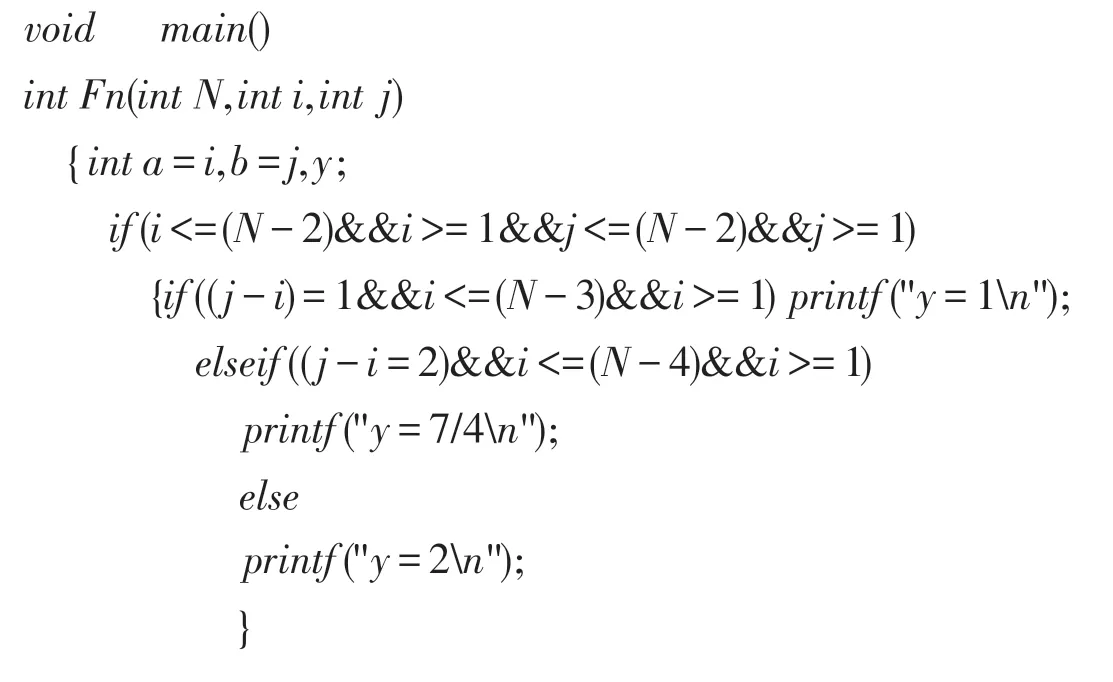
下面是该程序在n=20 时的运算结果部分截图：

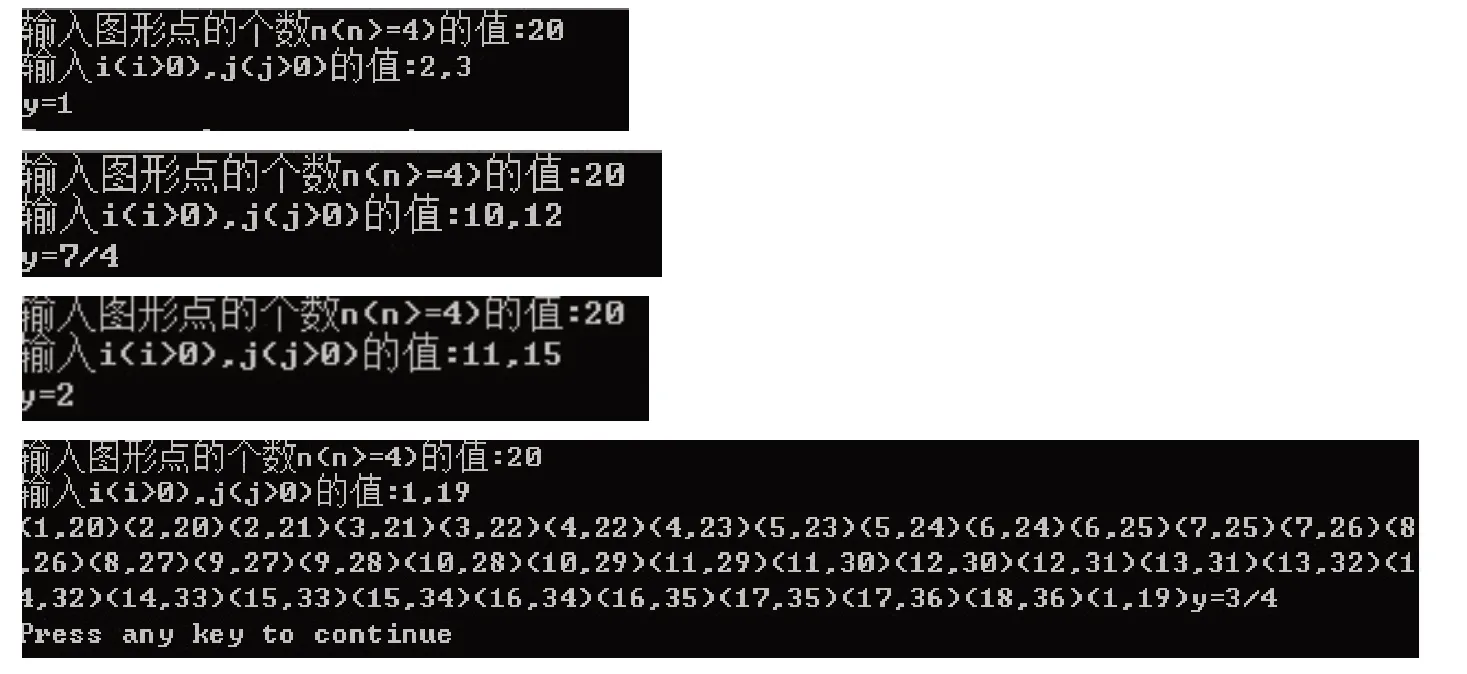
注1需要说明的是程序不仅输出了两边的平均距离，还输出了平均距离为的每对边和所有平均距离为的每对边.

定理1

证明对n进行数学归纳.

（1）当n=4 时，

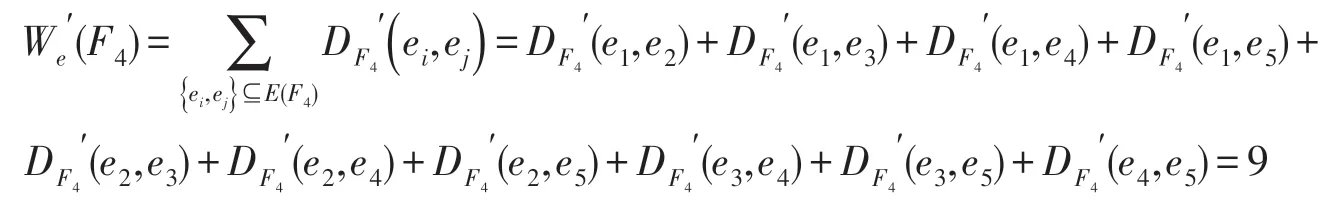
（2）假设等式对于n-1成立，即则

等式对于n也成立，定理得证.

3 n阶轮图Wn的边平均Wiener指标

定义2［7］Wn=Cn-1·V0表示具有n个顶点的轮图，其中Cn-1表示有n-1个顶点的圈，记

Cn-1的每一个顶点都与中心顶点V0连接，E(Wn)={v1v2,v2v3,…,vn-2vn-1,vn-1v1,v0v1,v0v2,…,v0vn-1}.记vivi+1=ei(i=1,2,…,n-2),v0vj=en-2+j(j=1,2,…,n-1),vn-1v1=e2n-2（如图2所示）.

图2 轮图Wn

Wn可以看做是在Fn的基础上连接e2n-2得到的.为了计算轮图的边平均Wiener指标，我们对轮图的边分为三类{e1,e2,…,en-2}，{en-1,en,…,e2n-3}和{e2n-2} 三类.计算的基础上，加需要注意的是，增加e2n-2，会导致在发生变化.

定理2We′(Wn)=3n2-11n+8 (n≥4).

证明Wn可以看做是在Fn的基础上连接e2n-2=v1vn-1得到的，故有

其中等式右边的第二项是由于Diam(Fn)=2，对任意x,y∈V(Fn)，有

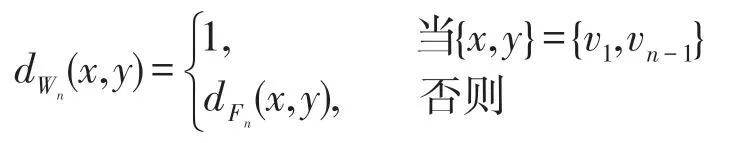
进而有，

故定理得证.

［1］DOBRYNIN A A，ENTRINGER R C，GUTMAN I.Wiener index of trees：Theory and applications［J］.Acta Appl Math，2001，66：211-249.

［2］IRANMANESH A，GUTMAN I，KHORMALIA O，et al.The edge versions of the Wiener index［J］.MATCH Commun Math Comput Chem，2009，61：663-672.

［3］WU B.Wiener index of line graphs［J］.MATCH Commun Math Comput Chem，2010，64（3）：699-706.

［4］蔡华，苗杰.n阶单圈图的边平均Wiener指标［J］.山东大学学报：理学版，2012，47（10）：70-74.

［5］蔡华，苗杰.n阶单圈图的边平均Wiener指标取整数的充要条件［J］.昌吉学院学报，2011，6：86-88.

［6］蔡华.图的边Wiener指标［D］.乌鲁木齐：新疆大学，2009.

［7］于玲，叶永升.路和圈的联的Wiener指数［J］.淮北师范大学学报：自然科学版，2011，32（1）：1-3.