电液伺服驱动的连铸结晶器位移系统反步滑模控制

方一鸣， 齐静， 李建雄， 许衍泽

(1.燕山大学工业计算机控制工程河北省重点实验室，河北秦皇岛066004;2.国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛066004)

0 引言

电液伺服系统具有响应速度快、提供的驱动力大等优点，因而得到了广泛的应用，如冷连轧机、连铸结晶器、航空航天等。然而在实际生产应用中，驱动连铸结晶器振动的电液伺服系统不可避免地存在内部参数和外部负载力的不确定性，使得系统的动态性能受到很大影响，同时给控制系统的设计带来很大困难。

目前许多学者针对这类问题采用不同方法进行了大量研究，如自适应控制，神经网络控制，模糊控制等。文献［1］针对电液伺服位置系统存在的参数不确定性及外部干扰，设计了一种鲁棒H∞控制器保证系统的稳定性;文献［2］采用自适应反步结合线性滑模的方法进行控制器设计;文献［3］将自适应模糊控制和backstepping方法相结合，采用模糊逻辑系统逼近等效控制部分，给出了自适应模糊滑模控制设计方法;文献［4］利用神经网络逼近系统不确定，采用反步方法逐步设计虚拟控制律，进而得到满足条件的控制器;文献［5］采用状态观测器对系统状态进行观测，并设计合理的控制器，使系统状态在不确定因素下能够跟踪给定。

在生产实际中，系统的状态通常是未知或难以测量的，因而在应用中设计观测器来估计系统状态便显得尤为重要;反步设计方法是一种将Lyapunov函数的选取与控制器的设计相结合的设计方法，该方法在逐步递推的设计过程中引入中间虚拟控制量，并基于Lyapunov稳定性理论给出整个系统控制器的设计方法;滑模变结构控制是一种有效的鲁棒控制方法，利用滑动模态的动态特性设计的控制器能有效抑制系统中的非线性环节的影响，具有较强鲁棒性。

本文结合比例积分状态观测器及反步滑模控制方法设计控制器，首先利用比例积分观测器对系统状态进行有效估计，并采用反步法设计虚拟控制量，最后一步与常规线性滑模不同的是本文引入非奇异终端滑模推导控制律，避免了传统终端滑模带来的奇异问题，并根据设计要求引入一类具有误差放大功能的类势能函数，同时为了抑制抖振问题引入饱和函数，并采用Lyapunov稳定性判定法证明系统稳定性。最后通过对电液伺服驱动的连铸结晶器位移系统进行仿真，进一步验证了所设计的控制器能够有效地提高系统的收敛速度和稳态跟踪精确度，使系统具有较强的鲁棒性。

1 连铸结晶器位移系统的数学模型

电液伺服驱动的连铸结晶器位移系统的结构主要由电液伺服阀、油源、对称液压缸和负载组成［6］。其常规控制系统示意如图1所示。

图1 连铸结晶器位移系统示意Fig.1 Schematic diagram of continuous cast mold displacement system

液压缸的基本方程式有3个:伺服阀流量方程，油缸流量连续方程以及活塞力平衡方程。

根据图1，定义负载压力PL=P1－P2;负载流量QL=(Qi+Qo)/2，忽略伺服阀的非线性，则伺服阀流量方程为

式中:Kq为流量增益;Kc为压力增益;xv为伺服阀芯位移。

把伺服放大器和伺服阀都等效成比例环节，因此有

式中:Kp为伺服放大器放大系数;Ksv为伺服阀增益;i为伺服放大器输出电流;u为伺服放大器输入电压。

定义 Kqsv=KqKpKsv，则式(1)变为

油缸流量连续方程为

式中:Ap为液压缸活塞有效面积;xp为油缸活塞位移;Ct为液压缸外泄漏系数;Vt为液压缸油腔总体积;βe为体积弹性模量。

活塞的力平衡方程为

式中:M为活塞和负载的总质量;Bp为活塞及负载的粘性阻尼系数;K为弹性刚度系数;FL为作用在活塞上的外负载力。

取状态x1=xp，x2=，x3=x¨p，x1，x2，x3分别代表活塞位移、速度和加速度，整理式(1)～(6)可得系统的状态空间表达式和输出方程为［6］

其中，

式中:u为系统输入;y为系统输出;d为参数不确定性及外部扰动。

因此，本控制目标是考虑系统式(7)中存在的参数不确定性及外部扰动等问题，通过设计合理控制器在保证系统稳定的同时实现精确位移信号跟踪，即位移信号x1能够跟踪给定位移信号x1d。

2 反步滑模控制器的设计

2.1 比例积分状态观测器的设计

在实际工业生产中，系统的状态通常是难以测量或未知的，因此在系统同时存在参数不确定性及外部扰动的情况下，采用以下状态观测器［5］对系统各个状态进行有效估计:

注1 由文献［7－8］可知采用传统比例状态观测器，增益矩阵L1选取越大，能使系统稳定性增强，然而会扩大干扰因素的影响，不能达到很好的观测效果，所以本文选择带有积分项的状态观测器。

定理1 考虑Lipschitz线性系统(7)，(A，C)可观，如果P、X满足线性矩阵不等式(10)，且满足P=PT＞0，X=PL1，λmin(PL2C)≥0，L 为 Lipschitz常数，则式(8)为系统渐近稳定的全维状态观测器［7］。

证明应用Schur补引理对不等式(10)进行变换得

再将X=PL1代入不等式(11)得

观测器误差动态方程为

选取Lyapunov函数，有

对式(13)求导得

存在

又存在

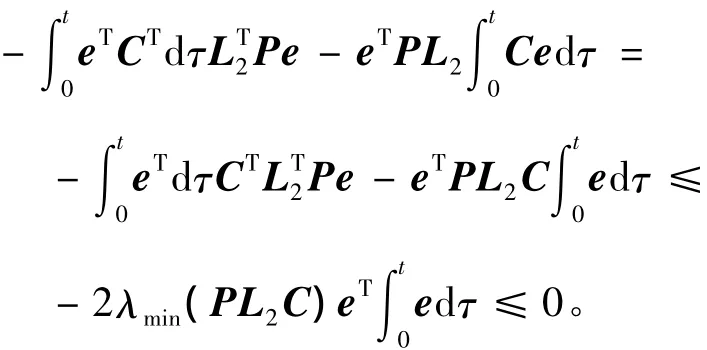
所以，有

所以系统渐近稳定，定理得证。

2.2 反步非奇异终端滑模控制器的设计

针对系统模型(7)采用 backstepping［9－10］进行控制器设计，并通过Lyapunov进行稳定性分析，其中，kj(j=1，2)＞0为控制器参数;为系统各状态观测值;x1d为位移给定信号;xid(i=2，3)为各阶子系统期望虚拟控制量。

控制器的设计步骤为:

Step 1 定义位移跟踪误差

对z1求导，有

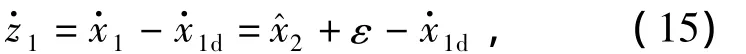
其中，ε=x2－。

并取Lyapunov函数，有

对式(16)求导，有

定义误差变量z2=x^2－x2d，其中x2d为虚拟控制量，取

Step 2 对z2求导，有

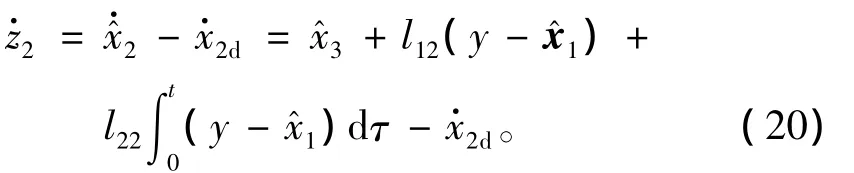
并取Lyapunov函数，有

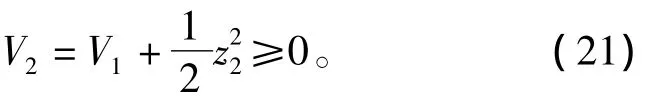
对式(21)求导，有

定义误差变量z3=－x3d，其中x3d为虚拟控制量，取

由式(22)和式(23)得

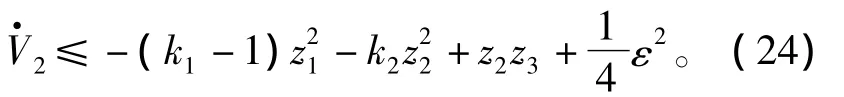
因此，由式(24)可知，若能保证z3收敛到零，则式(24)满足

其中，μ=2min{k1－1，k2}且保证 k1＞1，k2＞0 则满足子系统z1，z2稳定。

Step 3 与非奇异终端滑模控制方法相结合设计控制器使跟踪误差在有限时间内收敛。

由文献［11－12］启发，为了提高系统收敛速度和稳态跟踪精确度，引入一类类势能函数，即

式中:0＜α＜1，β＞0，且其对x求导得非线性饱和函数:

对于式(26)和式(27)所示的非线性函数有如下引理。

引理1 函数P(x)和p(x)有如下性质:

1)若 x=0则 P(x)=p(x)=0;若 x≠0则P(x)＞0。

2)P(x)连续可微，p(x)单调递增且p(x)≤βα。

由引理1给出的性质可以构造如下变换:

令

将以上函数与非奇异终端滑模面相结合构造如下滑模面［13－15］:

式中:γ＞0;p和q为奇数，且1＜p/q＜2。

注2 由引理1类势能函数的性质可知，该函数有小误差放大的作用，将其引入非奇异终端滑模能使所设计的控制器更快更准确地跟踪给定信号，且当误差为零时，该方法则退化为普通非奇异终端滑模方法。

设计控制律为

式中:

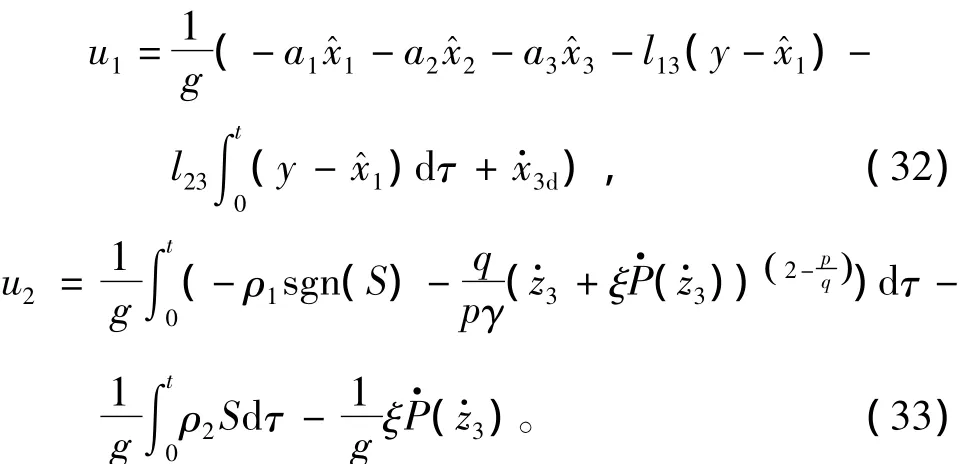
定义Lyapunov函数，有

将控制律式(31)、式(32)代入z3=x^3－x3d得

将控制律式(33)代入上式并求导得

为了减小抖振选取饱和函数代替符号函数，即

其中，δ为边界层宽度，在给定任意的初始值设计的滑模面函数S都将到达并保持在边界层|S|≤δ中。

3 仿真研究

为了验证该方法的有效性，以电液伺服驱动的连铸结晶器位移系统为仿真对象，其标称参数见表 1［6］。

表1 连铸结晶器位移系统参数标称值Table 1 Nominal parameter values of continuous cast mold displacement system

考虑到工业生产实际，采取正弦或非正弦信号为参考输入，因此仿真中的位移给定信号为

考虑实际中参数不确定性，选取扰动参数为

外负载力为

仿真中观测器参数设计如下

控制器参数设计如下

对普通非奇异终端滑模方法(ξ=0)以及文中改进方法(ξ=－0.1)，两种方法进行仿真比较，仿真结果如图2所示。

图2(a)为普通非奇异终端滑模与文中改进后的滑模相对应的跟踪对比曲线，可以看出在系统存在内部参数不确定性和外部负载力等不确定性情况下，两种方法均能保证系统稳定并准确跟踪给定信号，然而本文改进方法跟踪效果更好，系统鲁棒性更强;图2(b)为两种方法跟踪误差对比曲线，说明使用改进后的方法和普通非奇异终端滑模的方法所设计的控制器均能使系统具有更好的动态性能，但是采用本文提出的改进方法设计的控制器，系统收敛速度和稳态精确度更好(类势能函数的作用)。

图2 连铸结晶器系统状态曲线及滑模面曲线Fig.2 Time response of state of Continuous casting mold system and the curve of the sliding mode

4 结论

本文针对电液伺服驱动的连铸结晶器位移系统，考虑系统存在的参数不确定性及外部扰动因素，提出一种基于状态观测器的反步滑模控制方法。利用比例积分观测器对存在不确定性及扰动的系统状态进行有效估计，并通过反步法结合非奇异终端滑模设计合理的控制器。理论分析和仿真均表明，该系统在参数不确定性及外部扰动因素作用下，依然可以实现连铸结晶器位移信号的精确跟踪。

［1］ Milic'V，Situm Z，Essert M.Robust H∞position control synthesis of an electro-hydraulic servo system［J］.ISA Transactions，2010，49(4):535－542.

［2］ 方一鸣，焦宗夏，王文宾，等.轧机液压伺服位置系统的自适应反步滑模控制［J］.电机与控制学报，2011，15(10):95－100.

FANG Yiming，JIAO Zongxia，WANG Wenbin，et al.Adaptive backstepping sliding mode control for rolling mill hydraulic servo position system ［J］.Electric Machines and Control，2011，15(10):95－100.

［3］ 刘云峰，缪栋.电液的伺服系统的自适应模糊滑模控制研究［J］.中国电机工程学报，2006，26(14):140－144.

LIU Yunfeng，MIAO Dong.Research on adaptive fuzzy sliding mode control for electro-hydraulic servo system［J］.Proceedings of the CSEE，2006，26(14):140－144.

［4］ In S S，Jong M S，Han M K.Adaptive position control scheme with neural networks for electro-hydrostatic actuator systems［C］//Proceedings of the 2010 IEEE，International Conference on Mechatronics and Automation，August 4 －7，2010，Xi’an，China.2010:501 －506.

［5］ Prut N，Suwat K.Observer-based backstepping force control of an electrohydraulic actuator［J］.Control Engineering Practice，2009，17(8):895－902.

［6］ 方一鸣，韩永成，赵琳琳，等.控制量前具有不确定系数的电液伺服系统自适应控制［J］.控制理论与应用，2009，26(2):156－160.

FANG Yiming，HAN Yongcheng，ZHAO Linlin，et al.Adaptive controller for electro-hydraulic servo system with uncertain coefficients in control input［J］.Control Theory ＆ Applications，2009，26(2):156－160.

［7］ 杨洪金，井元伟，肇和平.非线性系统观测器的设计方法:LMI方法［J］.信息与控制，2011，40(4):433－437.

YANG Hongjin，JING Yuanwei，ZHAO Heping.Observer design for nonlinear systems:an LMI approach［J］.Information and Control，2011，40(4):433 －437.

［8］ HUA C C，GUAN X P.Synchronization of chaotic systems based on PI observer design［J］.Physics Letters A，2005，334(5):382－389.

［9］ Kwan C，Lewis F L.Robust Backstepping Control of Nonlinear Systems Using Neural Networks［J］.Systems，Man and Cybernetics，Part A:Systems and Humans，IEEE Transactions on，2000，30(6):753－766.

［10］ Madani T，Benallegue A.Backstepping control for a quadrotor helicopter［C］//2006 IEEE International Conference on Intelligent Robots and Systems，October 9 －15，2006，Beijing，China.2006:3255－3260.

［11］ 周丽，姜长生，都延丽.一种基于反步法的鲁棒自适应终端滑模控制［J］.控制理论与应用，2009，26(6):678－682.

ZHOU Li，JIANG Changsheng，DU Yanli.A robust and adaptive terminal sliding mode control based on backstepping［J］.Control Theory＆ Applications，2009，26(6):678－682.

［12］ 孙丽颖，赵军.考虑输入约束的发电机汽门非线性自适应控制［J］.控制理论与应用，2009，26(6):601－606.

SUN Liying，ZHAO Jun.Nonlinear adaptive control for the turbine steam valve with input constrains［J］.Control Theory ＆Applications，2009，26(6):601 －606.

［13］ 王坚浩，胡剑波.不确定非线性系统的自适应反推高阶终端滑模控制［J］.控制与决策，2012，27(3):413－418.

WANG Jianhao，HU Jianbo.Adaptive backstepping high-order terminal sliding mode control for uncertain nonlinear systems［J］.Control and Decision，2012，27(3):413－418.

［14］ Feng Y，Yu X，Man Z.Non-singular terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38(12):2159－2167.

［15］ Chuan K L.Nonsingular terminal sliding mode control of robot manipulators using fuzzy wavelet networks［J］.IEEE transactions on fuzzy systems，2006，14(6):849 －859.