初级绕组分段永磁直线电机段间推力优化控制

李立毅， 祝贺， 刘家曦， 马明娜

(哈尔滨工业大学电气工程及自动化学院，黑龙江哈尔滨150001)

0 引言

长行程直线电机在工业、军事应用中有着无可比拟的优势，由于采用直线电机直接驱动技术，省去了旋转到直线运动中的转换装置，从而减小了系统的复杂度，提高了系统的精确度和可靠性［1－5］。近年来，伴随着新型高性能永磁材料NdFeB的诞生，使得永磁同步直线电机优势更加明显，它具有推力密度高、重量轻、损耗低、响应速度快、可控性好等优点，可以保证直驱系统良好的品质因数［1，4，6］。但考虑当前永磁体的高昂价格，本文提出采用动磁钢结构的短次级长初级绕组分段永磁同步直线电机，从经济性角度考虑，它减少永磁体的使用量，节约了系统成本。从能源利用率角度看，仅需给与动子耦合的定子段供电，避免对初级绕组整体供电，有效的减小损耗，降低了逆变器容量，极大的提高了效率。另外，从维护制造的方面来看，初级分段结构还具有模块化特点，便于加工制造、方便拆卸组装、易于维护、应用范围灵活等优点［1－5，7－8］。

本文研究的初级绕组分段永磁同步直线电机(primary windings segmented permanent magnet linear synchronous motor，PWS－PMLSM)是由多个在电气上不连续的定子构成，各定子间紧密相邻。这种结构将导致动子在运动过程中必然要跨越各个段定子，随动子的位置变化电机的电感、磁链、推力系数、反电动势系数等参数也将发生改变。而且，各段定子内的电流如果不能很好地协调控制，将会造成各段电机推力大小不均衡，使动子在跨越段间运行时产生较大推力波动，甚至使两段电机间产生相互抵消的反向推力。在分段电机控制系统中，对电流调节的快速性、稳定性、以及段间电流的协调性将决定整个控制系统的优劣，因此本文重点要解决上述电流控制问题，达到减小段间推力波动、改善系统稳态和动态性能的目的。

本文首先根据电机的特点，提出了基于双逆变器交替供电模式下的段间电流同步跟踪控制策略，同时结合采用并联积分反馈环节、定子平均电流计算、定子电压解算、位置补偿、延迟补偿、参考值预测、电压极限校正等方法的PWM预测控制来实现段间推力优化控制。最后通过实验来验证上述方法的有效性。

1 电机的电磁参数分析与数学模型

定子铁心连续绕组分段的PWS－PMLSM原理如图1所示。

图1 定子铁心连续绕组分段的PWS－PMLSM原理Fig.1 Scheme of the PWS-PMLSM

本文以实验室两定子段样机为研究对象，经有限元方法对样机进行分析，得到电机的电磁参数变化规律，如图2中磁链、电感参数变化曲线所示。

图2 动子跨越定子段过程中的磁链、电感变化曲线Fig.2 Coupling flux linkage and inductance in the process of mover traverse among sators

磁链近似表达式为

式中:x为动子的实际位置;Sl1为第1段定子的长度;Ml为动子的有效长度;ψf－out(x)为动子移出定子段时初次极耦合磁链变化简化函数;ψf－in(x)为动子移入定子段时的耦合磁链的简化函数;ψf为永磁体在两段电机边界处与定子耦合磁链的总和。两段定子自感Ls1、Ls2变化规律与永磁体磁链类似，然而由于漏感的存在，当动子离开各段电机绕组时，电感幅值并不会完全减小到零。

上述分析可以得到依据动子位置变化的分段直线电机在d－q轴同步坐标系下的方程为

式中，Ls(x)，ψf(x)为随着动子位置变化的函数，而在非初级分段电机中它们均被视作恒值;v为动子运行速度;τ为极距。

根据矢量控制理论当采用id=0控制策略时，动子在两段电机边界处运动时所受推力是两段电机的电磁推力的总和，即

式中，pn为极对数。

2 初级绕组分段同步直线电机的段间电流同步跟踪控制

文中采用双逆变器交替供电策略，I号逆变器经电气开关与奇数段定子绕组连接(I=2n－1，n=1，2，3，…);II号逆变器经电气开关与偶数段定子绕组接(II=2n)。电气开关的通断由处理器负责控制。切换装置采用电力电子器件来实现，这样可以减小切换时间和切换过程中造成的电流波动。切换方法如表1所示。

表1 电流同步跟踪控制定子段使能表Table 1 Current synchronous tracking state

根据LR电路的原理，当动子将要到达到下一段定子边界处时，需提前t时间或x距离给下一段电机供电，以保证下一段定子电流稳定后接入系统，切断供电的定子绕组利用反相并联的续流二极管释放绕组线圈内的电流。定子供电切换时间与动子位置的关系表达式为

由式(3)、式(4)可以得出，通过合理的控制相邻两段定子绕组内的电流，就可以使两段的电磁推力之和保持平稳，如段内运行一样。

如果系统指令电流同时作为相邻两段定子的参考电流，由于各段定子控制器的动态响应能力的差异，将导致两段定子内的实际电流与系统给定的电流间都会有一定的误差和延迟，这样一来，就会使两定子段内的电流间产生更大差异、延迟，从而导致电机两段定子的励磁电流不完全同步，使得动子在跨越定子段的过程中会产生不可避免的推力波动。因此，本文提出相邻段间电流同步跟踪控制，段间电流同步跟踪控制原理如图3所示。

图3 段间电流同步跟踪控制原理Fig.3 Schematic diagram of the inter-segment current synchronous tracking control

如图3所示，根据动子与各定子段的耦合程度，确定主段定子lcouped＞Ml/2和从段定子lcouped＜Ml/2，lcoupled为动子与各定子段的耦合长度。在动子运动过程中，主－从定子段是随动子的位置变化而交替改变的，交替规律见表1。在动子穿越两相邻定子段交界处时，要求从定子段电流实时同步跟随主定子段的电流。该方法的优点是主－从段定子相互交替跟踪，可以实现从定子段内的电流实时与主定子段的电流同步，极大地减小各段间的电流差异，有效地抑制了段间推力波动，为动子在段间的平稳运行提供了保证。但在从定子段跟踪主定子段的过程中，由于从定子段的参考电流是主段中的实际电流，而它本身就含有一定的电流纹波，因此从定子段的电流纹波将更大一些。

式中:iM－ref为主定子段电流参考值为系统参考电流;iS－ref为从定子段的参考电流;iM－fed为主定子段实际电流。

3 改进的PWM电流预测控制及其在分段电机中的应用

3.1 分段电机电流预测控制模型

由于段间电流同步跟踪控制是以高电流响应能力为基础的，因此本文选择基于电机模型理论的PWM电流预测控制算法［8－12］来提高电流响应速度，更好地实现段间电流跟踪控制效果。

当采用数字处理器进行控制时，对系统的连续状态空间表达式(2)进行离散化，依据当前的实际电流在系统采样间隔Ts条件下的离散状态表达式，可以求出［k+1］th时刻定子段中的d－q轴电流，即is(k+1)的时域解为

如果系统采样时间Ts足够小，能够满足香农采样定理的要求，上式就可以简化为

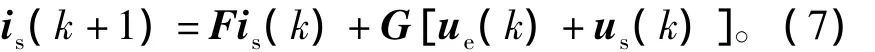
式中

如果令is(k+1)－(k+1)=0，即使用［k+1］th时刻的系统参考电流(k+1)取代表达式(8)中的is(k+1)，就可得出需加在逆变器上的电压，即

式(8)是电流预测控制的基本原理，理论上定子电流在第［k+1］th控制周期完成对指令电流的无差跟随，即在一个控制周期内完成零电流误差控制。

3.2 电流预测控制算法的改进与优化

在实际应用中，由于现有数字处理器(digital signal processing，DSP)的硬件结构及工作原理的限制，如采样转换时间、PWM信号更新延迟、数字滤波以及保持器的使用等，将导致如下问题产生。系统期望在［k］th控制周期开始对各信号进行采样，在［k－(k+1)］th时间内完成对的计算，然后在［k+1］th周期生成控制控制电压，并产生 PWM控制信号。但由于PWM信号更新延迟的问题，即DSP中的PWM信号更新必须要与控制周期同步执行，所以要等到［k+2］th时刻才可以应用到逆变器上。整个采样、计算、执行过程需要延迟两个控制周期才完成，也就是［k+2］th时刻才能使实际电流跟随上指令电流。这就当于在控制系统中引入一个滞后环节，改变了系统的零极点，将会影响到控制系统的带宽，甚至会导致系统震荡发散。

为了消除数字控制系统这一固有延迟，提高预测控制器的性能，必须对此延迟环节加以补偿。假定被选择的电压矢量在［k+1］th时刻应用，就需要去预测［k+2］th时刻的电流值。将式(7)向前推算一个PWM周期，则可推导出［k+2］th时刻的电流预测值为

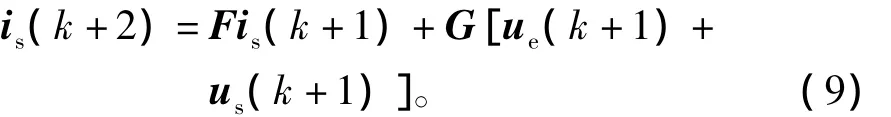
由式(9)可以看出，两周期之后的电流矢量is(k+2)是由前一时刻的电流矢量和电压矢量共同决定的，所以将式中的［id(k+1)，iq(k+1)］T用式(8)替代，并近似的认为ue(k)=ue(k+1)，可推导出is(k+2)、is(k)和 us(k+1)的关系式，即

根据式(10)就可估算出在第k+1时刻实施到逆变器上的控制压［(k+1)(k+1)］T，即

这时令is(k+2)=(k+2)，这里(k+2)是当前时刻估算得到的［k+2］th时刻参考电流矢量，带入式(11)就是系统延迟补偿的PWM电流预测控制。

延迟补偿PWM预测控制的思想，不仅关注被控对象下一时刻的预测值，还要对目标值进行超前预测，也就是不但要使实际的电流值尽可能接近参考电流值，还要获得准确的参考电流值来实现延迟补偿。如果希望在［k+2］th时刻的电流矢量预测值与该时刻电流矢量给定值相同，就需要在［k］th时刻对［k+2］th时刻的参考电流矢量进行提前两步预测，来获取准确的［k+2］th时刻参考电流矢量。

在控制周期Ts为恒定值的前提下，可以使用拉格朗日抛物线二阶插值法或线性插值法，依据当前时刻参考电流矢量和先前时刻的参考电流矢量，求出下一拍的预测电流参考矢量。

二阶插值法为

根据式(12)在再向后预测一拍可以得到

对于采样周期Ts足够小的系统，可也近似的认为

选择不同的参考电流预测法，将会对定子电流的暂态响应速度、相位延迟及超调量等方面产生不同的影响，可以根据具体情况而定。

PWM电流预测算法还存在对系统参数变化过于敏感，对电机模型依赖度高，受直流母线电压波动、定子电压极限以及开关死区时间影响等问题。它们都会影响控制精确度，曾加系统的不稳定性。

考虑到逆变器开关死区时间的存在，每个控制周期内作用在电机定子上的实际电压值与理想值us(k)并不相等，所以直接使用us(k)进行计算是不准确的。为解决这一问题，可以利用相电压重构法，通过直流母线电压udc和逆变器开关信号(s1，s2，s3)的占空比求得dq坐标系下的电压精确值s(k)，即

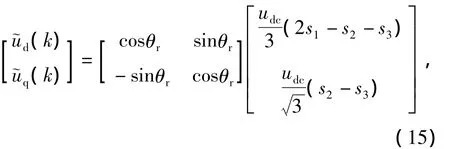
考虑到SVPWM算法的基本原理，每个控制周期内的电压值是开关信号在一个周期内的平均作用效果，所在计算定子电阻压降和反电势电压时也需要采用一个周期内平均值来计算。根据［k～k+1］th和［k+1～k+2］th控制周期内电枢电流呈线性变化的规律，则每个控制周期内的平均电流表达式，可以通过式(16)近似得到，即

用式(16)替代式(10)中的is(k+1)，is(k+2)最终可以得到

根据延迟补偿电流预测控制算法的原理，控制系统是在［k］th控制周期对电机位置进行采样得到动子位置信号，［k+1］th时刻计算出参考电压(k+1)，需要等到［k+2］th控制周期实施。从位置采样到控制电压实施的过程中，动子位置的偏差信号，并将它将其转换成位置角后为

由式(18)可以看出，当电机控制周期Ts较短，或运行速度v较小，或电机磁极对数pn不多时，这一偏差可以忽略不计。当电机高速运行时，对于高速高性能控制系统而言，这一角度偏差则不可忽视(可以达到几十度的电角度误差)，否则会使控制效果变差，导致电流波动。为此在计算(k+1)的过程中需要对动子位置角进行补偿，位置补偿角Δθoffset的计算方法为

对于电机系统参数变化或参数测量误差，以及直流电压波动的影响，尤其是在分段电机中，各段间电磁参数变化剧烈很难取得良好的控制效果。为了减小这些因素对控制系统的影响，本文采用带有并行积分补偿环节的PWM电流预测跟踪控制。在电机启动/停止或动态运行过程中，仅预测控制环节工作，从而提高系统动态响应性能。当电机处于稳态运行时，积分环节和预测环节同时工作，由积分补偿环节来抑制系统参数变化或直流母线电压波动对控制系统精确度的影响，即由积分补偿环节来消除稳态电流的累积误差，两个环节的输出电压值之和作为控制电压驱动逆变器工作，即

式中:Ureal(k)为实际加在逆变器上的控制电压;uerror(k)为在系统参数改变或系统模型不准确条件下的电压预测值;Δuoffset(k)为积分校正环节输出的补偿控制电压。

最后，经计算得到的理想控制电压Ureal(k+1)并不可以直接加在逆变器上。因为当系统的给定值发生剧烈变化时，这一理想电压的幅值可能会超过逆变器提供的电压极限，此时就要对控制电压进行校正。由于受到三相逆变器线性调制范围的限制，当直流母线电压为udc时，经坐标变换后，在同步旋转轴系下所能提供的最大值电压仅为

如果式(20)计算出同步旋转轴系下的电压值［ud(k+1)，uq(k+1)］T不符合式(21)，就需要对它们进行如下校正，即

3.3 控制系统总体结构

基于SVPWM的分段电机电流同步预测踪控制系统主要由速度调节器、两组逆变器及控制它们的两组电流预测控制器构成。当动子运行时，先由主－从判定器来确定各段定子的主从关系，主段定子段电流预测控制器的输入信号包括速度调节器输出的q轴参考电流值，再经插值计算得到它下两拍的估算值、动子速度反馈值和该段自身的d－q轴的电流采样值。从定子段的预测电流控制器的输入信号包括主定子段的q轴实际电流经过插值计算得到的下两拍的电流估算值、动子的速度反馈值及自身的d－q轴电流采样值。从而实现了彼此交替预测跟踪，完成段间电流同步无误差控制。各定子段的d轴电流均采用id=0方式。两组逆变器与各段定子的连接使能，也由基于位置传感器的定子段选择器来裁决。在奇数段和偶数段控制器的电流控制环节上分别并联了一个积分补偿回路，用以消除稳态误差提高系统鲁棒性。补偿模块由两组积分器构成，它们的输入分别为交直轴的误差分量。补偿回路经积分运算后得到的电压补偿值Δud、Δuq与预测模块的输出电压ud，uq分别求和，经电压校正环节输出到逆变器上，带有积分补偿通道的段间电流预测跟踪控制原理如图4所示。

图4 带有积分补偿通道的段间电流预测跟踪控制原理Fig.4 The block of inter-segment current tracking and predictive control with the loop of integral compensation

4 系统仿真测试

4.1 动子移出定子段过程仿真

仿真条件为:PWM频率为20 kHz;速度指令为3 m/s;负载推力为200 N。图5为单段定子运行仿真效果。

图5 单段定子运行交轴电流、电磁推力、三相电流仿真图Fig.5 Simulation of q-axis current，electromagnetic force and three-phase current curves when mover runs on stator

图5(a)为单段定子的交轴电流变化曲线，随着动子的逐渐移出该段定子，即0.14 s时刻开始，为了维持恒定的电磁推力，交轴电流幅值不断加大，最终达到输出限幅值。从图5(b)中可以看出，在0.14～0.165s时间内可以依靠提高交轴电流幅值来保持推力平稳，但随着动子与这段定子的耦合程度不断减小即从0.165 s开始，仅依靠提高定子的交轴电流幅值也无法到达平稳的推力。当动子最终移出该段时，该段产生的电磁推力变为零。图5(c)为该定子段三相电流曲线，它与交轴电流变化规律相似。

4.2 段间电流跟踪控制算法对比分析

系统仿真条件为:PWM频率为20 kHz;速度指令为3 m/s(0～0.25 s)和 －3 m/s(0.25～0.5 s);负载推力为恒定400 N。图6(a)和图6(b)均为未采用段间电流跟踪控制的电流预测控制仿真效果;图6(c)、图6(d)、图6(e)为采用段间电流跟踪控制的仿真效果。

图6(a)表示动子在跨越相邻两段定子时，它所受到的两段电机的电磁推力及合力曲线，F1为第一段电机产生的电磁推力，F2为第二段定子产生的电磁推力，F1+F2为两段定子推力之和的拟合曲线。从图中不难看出，在动子跨越段过程0.14～0.21 s，0.35～0.42 s两段电机的电磁推力之和会产生明显的波动。图6(b)表示的是两段电机的交轴电流变化曲线，仿真效果反应出，两段电机的交轴电流并不完全一致，这一点与前文的理论分析完全吻合，两段电流会有一定的偏差，恰恰就是这一偏差导致了段间推力波动的产生。

从图6(c)中可以发现动子在跨段过程中几乎无推力波动。从图6(d)中观察得到，从定子段的q轴电流纹波比主定子段的稍微大一些，这是因为从定子段的参考电流本身就存在一定的纹波，但两段定子的电流中心线 (水平虚线)还是保持一致，因此不会产生图6(a)中那样明显的推力波动。图6(e)为三相电流交替跟踪的效果，在t1～t3(0.14～0.21 s)，t4～t6(0.35～0.42 s)跨段过程中两组三相电流的同步程度很好。

图6 未采用/采用电流同步跟踪预测控制方法电机运行效果对比Fig.6 Simulation of predictive control without and with inter-stator current synchronous tracking control

4.3 改进电流预测算法的动态响应性能仿真

为验证本文所提出的改进电流预测控制算法的动态性能，系统仿真运行条件为:PWM频率为20 kHz;负载推力为80 N;指令电流信号在0.1 s时从1 A跳变到2 A，采用改进的电流预测控制算法进行仿真测试。图7(a)为指令电流发生跳变时定子段中实际电流的跟随效果，图7(b)为其局部放大图。由图7(b)可见，实际电流经过0.1 ms就完全跟随上指令电流，整个工作过程在两个控制周期内完成。传统的PI电流调节方式则很难达到如此高的动态响应能力，还将不可避免地产生振荡调整过程和较大的超调量，而预测控制则避免这样的问题。

图7 改进后的电流预测控制算法暂态仿真效果曲线Fig.7 Effect of improved predictive control under the transient performance

5 系统实验测试

为了验证本文所提出的控制方法，以一台隐极式PWS－PMLSM为控制对象，电机具体结构如图8所示。电机主要参数为:每段定子长度为0.6 m;动子长度为0.24 m;定子电阻为50 Ω;初次极完全耦合时定子电感值为35.8 mH;动子完全移出后定子电感为28 mH;电机极数为4;动子质量为5 kg;永磁磁链为0.88 Wb;直流母线电压为300 V。

图8 实验样机结构Fig.8 Outline of experimental device

控制系统采用TI公司的TMSF28335DSP控制芯片为核心，系统控制频率(中断、采样、PWM)为10 kHz，逆变装置采用两块三菱公司的IPM模块，位置检测装置是具有1 mm精确度的GIVI磁栅尺。首先是对一段定子，包括动子逐渐移出该段的运行效果进行试验测试。控制方法采用基于SVPWM调制方式的电流预测算法。

5.1 单段定子运行实验

从如图9所示的单段电机运行三相电流的实验波形中可以看出，当动子逐渐移出该定子段的过程中(第二段is2=0)的情况下，其运行效果与仿真结果完全吻合，充分说明了算法与模型的准确性。

图9 单段电机运行三相电流效果Fig.9 Experiment of three-phase current curve when mover runs on single stator

5.2 未加系统延迟补偿及相关改进算法的传统电流预测控制

图10为未加改进的电流预测控制实验效果，控制系统速度环节采用PI控制，而电流环节采用传统的电流预测控制算法。系统以2 m/s的匀速运行，图10(a)为第一段电机的三相电流波形(包括启动过程)，图10(b)为第二段电机的三相电流波形(包括动子进入这一段的过程)。从实验结果中不难看出，未采用系统延迟补偿和相关优化算法的条件下，系统电流文波较大，震荡明显，稳态误差大，控制效果不佳。

图10 未加改进的电流预测控制实验效果图Fig.10 Experiment of three-phase current curves of conventional PWM predictive current control

5.3 算法改进后的预测电流控制

图11为改进后的电流预测控制实验效果，图11(a)为第一段定子中的三相电流，图11(b)为第二段定子中的三相电流。从实验结果中可见，动子在运动过中各段定子三相电流变化平稳，动子跨越段边界过程中第二段电流跟踪速度快，几乎无抖动和超调现象，整个过程中电流文波较小，效果明显优于传统的电流预测控制方法。

图11 改进后的电流预测控制实验效果Fig.11 Experiment of three-phase current curves of improved PWM predictive current control

6 结语

针对改进的电流控制算法及段间电流交替跟踪策略，分别在系统动态响应能力、稳态性能和抑制动子跨段过程中的段间推力波动等方面进行研究。通过仿真和试验的方法对各算法进行验证，并取得了一致的效果。经验证得到，段间电流跟踪控制可以有效地抑制动子跨段过程中的推力波动。改进的电流预测控制，在提高系统动态响应能力和稳态运行效果上有着明显的优势，也给段间电流交替跟踪策略提供了基础。两者的有机结合使得初级分段式永磁同步电机的运行效果得到了极大的提升，初步克服了初级绕组分段结构对电机运行的影响。

［1］ 上官璇峰，励庆孚，袁世鹰，等.不连续定子永磁直线同步电动机运行过程分析［J］.西安交通大学学报，2004，38(12):1292－1296.

SHANGGUAN Xuanfeng，LI Qingfu，YUAN Shiying，et al.Analysis on running process of permanent linear synchronous motors with discountinuous stators［J］.Journal of Xi’an jiaotong University，2004，38(12):1292－1296.

［2］ LEIDHOLD R，MUTSCHLER P.Speed sensorless control of a long-stator linear synchronous motor arranged in multiple segments［J］.IEEE Transactions on Industrial Electronics，2007，54(6):3246－3254.

［3］ SUZUKI K，KIM Y J，DOHMEKI H.Driving method of permanent-magnet linear synchronous motor with the stationary discontinuous armature for long distance transportation system［J］.IEEE Transactions on Industrial Electronics，2012，59(5):1090 －1095.

［4］ 上官璇峰，励庆孚，袁世鹰.多段初级永磁直线同步电机驱动的垂直提升系统［J］.中国电机工程学报，2007，27(18):7－12.

SHANGGUAN Xuanfeng，LI Qingfu，YUAN Shiying，The vertical hoist system driven by PMLSM with multi-segment primary［J］.Proceedings of the CSEE，2007，27(18):7 －12.

［5］ KINJIRO Yoshida，HIROSHI Takami，AKIHIRO Fujii.Smooth section crossing of controlled repulsive PMLSM vehicle by DTC method based on new concept of fictitious section［J］.IEEE Transactions on Industrial Electronics，2004，51(4):821－826.

［6］ ROVERS J M M，JANSEN J W，LOMONOVA E A.Novel force ripple reduction method for a moving-magnet linear synchronous motor with a segmented Stator［C］//Proceeding of the 11th International Conference on Electrical Machines，October 17 － 20，2008，Wuhan，China.2008:2942－2947.

［7］ PIAO A H，KOHNO B S，SUZUKI C K，et al.Development of the change circuit of the inverter of intermittent stator PM-LSM［C］//15th International Conference on Electrical Machines and Systems，October 21－24，2012，Sapporro，Japan.2012:6401852.

［8］ 洪俊杰，李立毅.基于电流误差矢量的绕组分段永磁直线同步电机电流预测控制［J］.中国电机工程学报，2011，31(30):77－84.

HONG Junjie，LI Liyi.Current error vector based prediction control of current in segment winding PMLSM［J］.Proceedings of the CSEE，2011，31(30):77－84.

［9］ SPRINGOB Lothar，HOLTZ Joachim.High bandwidth current control for torque-ripple compensation in PM synchronous machines［J］.IEEE Transactions on Industrial Electronics，1998，45(5):713－721.

［10］ MOON Hyung-Tae，KIM Hyun-Soo，YOUN Myung-Joong.A discrete-time predictive current control for PMSM［J］.IEEE Transactions on Power Electronics，2003，18(1):464 －472.

［11］ MOREL Florent，XUEFANG Lin-Shi，RETIF JeanMarie.A comparative study of predictive current control schemes for a permanent magnet synchronous machine［J］.IEEE Transactions on Power Electronics，2009，56(7):2715 －2728.

［12］ 瞿博，洪小圆，吕征宇.模糊控制在三相PWM整流器无差拍控制中的应用［J］.中国电机工程学报，2009，29(15):50－54.

QU Bo，HONG Xiaoyuan，LU Zhengyu.Application of fuzzy control theory to deadbeat control scheme in three-phase pluse width modulation rectifier［J］.Proceedings of the CSEE 2009，29(15):50－54.