大功率随动试验台多永磁同步电机同步控制
姜晓平, 朱奕, 伞冶
(哈尔滨工业大学航天学院,黑龙江哈尔滨150001)
0 引言
大功率随动试验台广泛应用于随动系统的试验检测装置中,用来为待测试的随动系统提供负载模拟环境。快速性是衡量试验台性能的一个主要技术指标。对于大功率试验台,其台体转动惯量很大,若采用单电机驱动,即使控制系统被开发到最大程度也无法满足快速性要求,因此需要考虑提高系统执行机构的伺服能力,最常用的办法是采用多电机驱动。
多电机共同驱动负载时,由于系统传动机构中存在齿隙,若各个电机之间存在转速差,则会存在部分齿轮在齿隙间游走的状态,此时与这部分齿轮相连的电机并不产生驱动负载作用,这将严重影响系统的快速性,因此要求各电机之间保持同步运行关系,只有这样,才能保证各个电机共同分担驱动力矩,实现快速性要求。可见,多电机同步控制的研究具有非常重要的现实意义。此外,在舞台、船舶等诸多领域广泛应用的升降平台[1],对同步精确度也提出了很高的要求。
多电机同步控制系统主要包含同步控制结构和同步控制算法两个方面,优越的控制结构配合合适的控制算法就可以获得良好的同步效果。早期的同步控制结构主要采用的是非耦合结构,主要包括并行和主从两种结构,二者同步效果较差。针对这种情况,上世纪80年代初Koren提出交叉耦合控制策略[2],把耦合的思想引入到同步控制中,但该结构只能用于两电机之间的同步。鉴于此,Francisco等人于2002年提出了偏差耦合控制策略[3],该结构对电机数量没有任何限制,并且充分继承了交叉耦合控制的思想。但是,随着电机数量的逐渐增多,偏差耦合控制的结构也越来越复杂,Dong Sun[4]和张承慧[5]等人从简化控制结构的角度出发,于2007年提出了相邻交叉耦合控制策略,在保证同步效果的同时大大简化了同步系统结构。
针对具体的同步控制结构,许多学者进一步研究了同步控制算法,诸如内模控制[6]、最优轮廓控制[7]、模糊 PID 控制[8]、自适应前馈控制[9]、滑模变结构控制[10]等,每一种算法均是针对具体的应用背景而提出。在由4台永磁同步电机驱动的大功率随动试验台中,影响多电机同步的因素主要分为两方面,一是交流伺服子系统相对应的元器件的参数不尽一致且会发生不同程度的摄动;二是子系统会受到随机扰动的影响,因此鲁棒性应成为试验台控制方法选择时的一个重要方面。而滑模变结构控制正是由于其突出的鲁棒性而得到研究人员的重视,同时它比较简单,便于理解和应用,易被工程人员所接受,因此,滑模变结构控制适合于试验台的多电机同步控制。
本文针对大功率随动试验台中4台永磁同步电机的同步控制问题,在相邻交叉耦合同步控制结构的基础上,针对试验台自身的特点,将滑模变结构控制引入到多永磁同步电机的同步控制结构算法中,设计了多电机同步滑模控制器,实现了多电机的同步控制,并分析了所设计的同步控制系统的鲁棒性,通过仿真来验证该控制策略的有效性。
1 大功率随动试验台机械结构
大功率随动试验台机械结构的剖视图如图1(a)所示,俯视图如图1(b)所示。
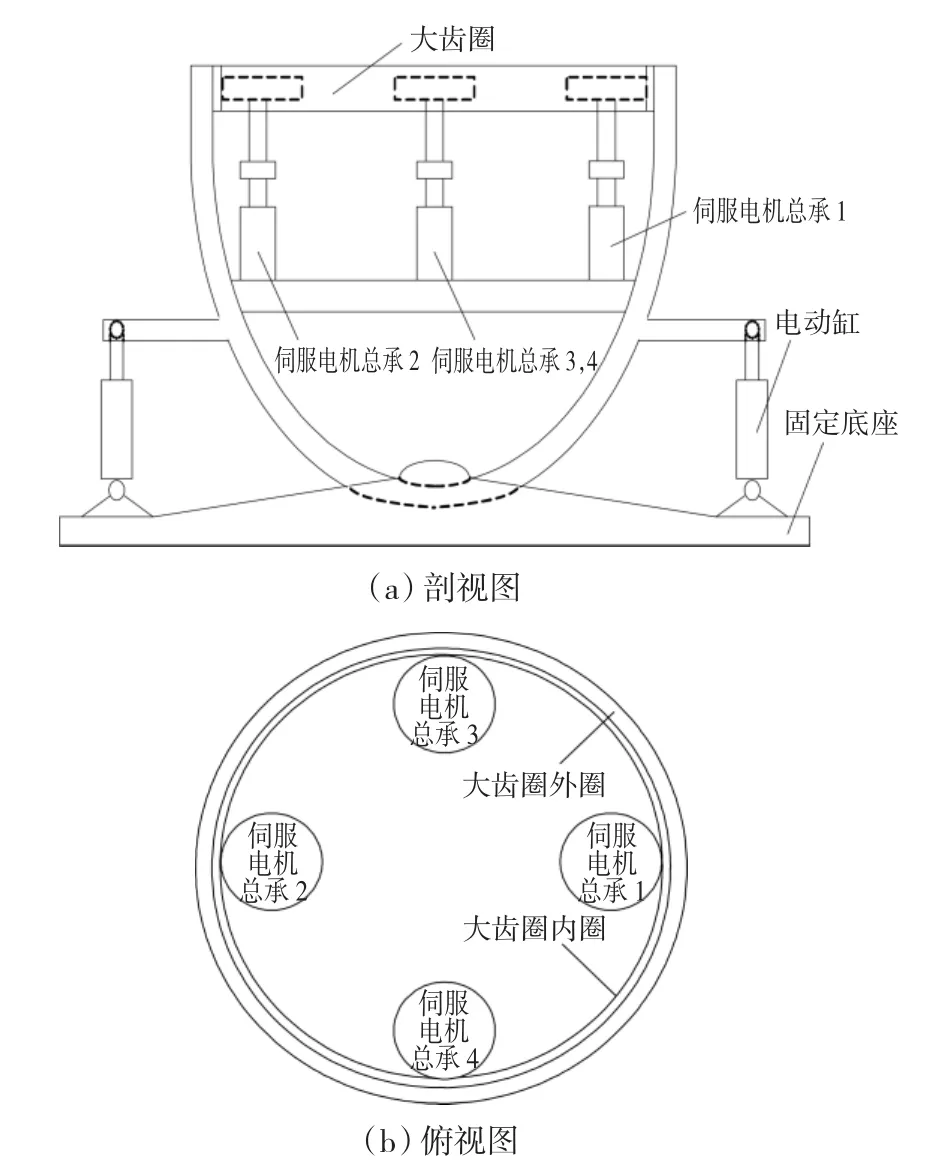
图1 随动试验台机械结构Fig.1 Mechanical structure of servo test stands
试验台机械台体的主体部分是一个类似半圆球的结构,在其顶部的横切面上,紧贴内表面安装了一个大齿圈,大齿圈转动模拟一定的方位运动。机械台体中的4个伺服电机,即图中的伺服电机总承1、2、3和4,均选用正弦波驱动永磁同步电动机,整体采用对称立式结构的布局,各个电机分别通过减速器来驱动与之相应的小齿轮,小齿轮与大齿圈内圈啮合,这样,4个电机转动从而共同驱动大齿圈转动。安装在台体固定底座上的一对电动缸用来控制台体的倾斜运动。此外,为了满足开放式试验平台的要求,机械台体中还预留位置安装负载模拟电机和干扰模拟电机,并且伺服、负载及干扰电机三者之间可以根据实际需要进行任意的角色转换。
2 相邻交叉耦合同步控制结构
偏差耦合控制结构中每个速度补偿器均需要所有子系统的速度反馈信号作为输入,相邻交叉耦合控制结构[10]正是从这一点出发对偏差耦合结构进行了简化,其结构如图2所示。

图2 相邻交叉耦合控制结构Fig.2 Structure of adjacent cross-coupling
该结构同样采用了补偿的思想,但是每个速度补偿器只需要其所在的子系统及与其相邻的两个子系统的速度反馈信号作为输入,也就是说,每个速度补偿器的输入信号总数恒为3,此处以速度补偿器1为例,其结构如图3所示,子系统1的速度反馈信号ω1分别同子系统2的速度反馈信号ω2和子系统4的速度反馈信号ω4作差,两差分别通过增益K1和K2进行补偿后得到子系统1的速度补偿信号。

图3 速度补偿器1结构Fig.3 Structure of speed compensator 1
此外,在进行子系统扩展时,偏差耦合控制结构需对原系统中的每一个速度补偿器进行改动,而相邻交叉耦合控制结构只需对原系统中与扩展子系统相邻的两个速度补偿器进行改动,工作量大大降低,因此相邻交叉耦合控制结构比偏差耦合控制结构更易进行子系统扩展,能够满足大功率随动试验台开放性的要求。
3 永磁同步电机数学模型
多电机同步控制的主要目标便是使每两个电机间的同步误差趋于零,按照相邻耦合控制结构的思想,同步误差趋于零便可转化为每个子系统的速度补偿信号趋于零,以速度补偿器1的输出 ε1为例,即

式中,t为时间变量。
由于4台伺服电机选用的是同一型号的永磁同步电机,因此速度补偿增益K1和K2近似为1,此时可以得到

这意味着在同步过程中电机1跟踪电机2和电机4转速信号的均值,在设计控制器时,为简化设计过程,可以将电机2和电机4转速的均值看作一待跟踪的常量,此时,完全可以按照阶跃信号跟踪控制器的设计方法来设计同步误差控制器。
当采用直轴电流id=0的矢量控制方式时,忽略系统的粘滞摩擦力,可得

式中:ωm为电机转子机械角速度;p为电机极对数;ψr为永磁体基波励磁磁场链过定子绕组的磁链;J为转子和电机所带负载的总转动惯量;iqr为将电流闭环近似为增益为1的比例环节后的交轴电流;T为负载转矩。
交流伺服系统处于稳态时,要求其跟踪误差为零,为此,需保证在系统的动态过程中,跟踪误差及其积分量收敛并趋于零。鉴于此,选择系统的跟踪误差及其积分量作为状态变量[11],具体定义为

式中,ωref为机械角速度参考信号。由此可得系统的状态方程为

4 滑模控制器设计
为了保证系统的快速性,所以要求跟踪误差有较快的收敛速度。若能使跟踪误差以指数形式渐近收敛至零,则可完全满足快速性要求,此时跟踪误差e(t)须满足

用状态变量表示,即为

由于x2=x·1,所以

对于滑模变结构控制系统,系统状态必然从滑模面的两边向滑模面靠近,然后沿滑模面趋向于稳定的平衡点。在系统处于滑模面期间,切换函数s保持为零,因此系统状态满足方程s=0和s·=0,将上述两式结合来看,不难发现,可取切换函数

此时跟踪误差以指数形式渐近收敛至零。
设计滑模变结构控制系统时,首先要保证滑动模态满足存在性及可达性,即

将系统的状态方程代入式(10),可得

为使式(11)成立,构造

若能满足

则式(11)必然成立。由式(13)可得

根据扩展的李亚普诺夫定理[12],构造李亚普诺夫函数
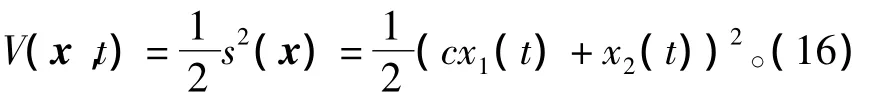
式中:x为状态向量;t为时间变量。很容易证明前面设计的滑模变结构控制系统是渐近稳定的,稳定点为原点。
滑模变结构控制是建立在控制开关的频繁切换,即要求开关频率足够大的基础上的,由于滞后等因素在实际系统中的不可避免性,多电机同步控制系统中会出现抖振。抖振会带来稳态误差,同时将不停地消耗系统的能量,甚至可能激发系统的高频振动。为了削弱其不利的影响,可以采用边界层法[13]来加以抑制。
对于开关切换函数

引入线性段使其连续化,将其变成饱和函数sat(s),具体实现方法为

式中,λ为常数且满足λ>0。函数图表示如图4所示。
引入sat(s)来代替sgn(s)后,原来的开关型系统变为连续系统,连续系统仍会在切换面附近产生高增益1/λ来维持滑模运动。此时虽然也存在滞后,从而使系统产生抖振,但是此时的滞后相对于连续系统来说较小,与开关型系统相比,抖振的程度大为削弱。

图4 边界层法Fig.4 Boundary layer method
5 同步控制系统鲁棒性分析
为了方便设计控制器,同步电机的数学模型中忽略了粘滞摩擦等因素的影响,现考虑更精确的模型

式中,B为摩擦系数。
考虑到大功率试验台中参数摄动和随机扰动的影响[14],进一步将系统模型表示为

现在考察一下滑模变结构控制中滑模运动段对参数摄动Δa和随机扰动d(t)的鲁棒性。对滑模变结构控制中的切换函数进行求导可得

由前文知控制量u=kx2+ηsgn(s)。切换面上的滑动模态满足s=cx1+x2=0,当s>0时,由可达性条件式(10)可知<0,即


若记 α=(ca+cbk-c2)+(cΔa),则


该模态区完全不受摄动和干扰的影响,体现了多电机同步滑模控制系统的强鲁棒性。
6 仿真实验及分析
工程实践中虽选用4台同一型号的永磁同步电机作为伺服电机,但考虑到在实际情况中,即使是同一型号的电机,其对应的各项参数间也会有细微的差别,本文按照±1%误差界限的原则,对4台电机仿真模型中的各个参数进行随机选取,取值见表1。表中Rs为定子绕组电枢电阻,Ld为直轴(d轴)电感,Lq为交轴(q轴)电感。

表1 4台永磁同步电机参数Table 1 Nominal parameters of four motors
在Matlab/SIMULINK环境下,根据4台永磁同步电机的参数,首先完成单电机伺服系统的设计,然后按照偏差耦合和相邻交叉耦合同步控制结构(图2及图3)设计4电机同步控制系统的仿真模型。4台电机的控制系统是类似的,以电机1为例,其控制系统总体控制框图如图5所示,系统采用id=0的矢量控制方法,同步控制器的输出信号直接补偿电机的交轴电流iq。偏差耦合结构中采用PI控制作为同步控制算法,其中比例系数取值为3.4,积分系数取值为0.14,相邻交叉耦合结构中分别采用PI控制和抑制扰动的滑模控制,PI控制与偏差耦合结构中PI控制的相应系数相同,即比例系数取为3.4,积分系数取为0.14,3个同步系统的速度参考信号均为1 400 r/min。
考察4电机的速度同步情况时应表示出每两个电机间的速度同步误差,总计6组数据,但考虑到这6组数据间不是相互独立的,因此可以减少数据组数,以避免内容繁杂冗余。本文只表示了电机2、3和4的速度分别与电机1的速度间的同步误差,共3组数据,如图6、图7和图8所示,其中图6为偏差耦合结构下的同步误差,图7为相邻交叉耦合结构和PI控制下的同步误差,图8为相邻交叉耦合结构和滑模变结构下的同步误差。其余的同步误差均可由这3组数据求解得到,故不再罗列。同时为了增强同步误差数据的可读性,本文将同步误差用其相对于参考速度的百分比来表示。

图5 永磁同步电机1矢量控制系统Fig.5 Vector control of synchronous motor 1
为了考察同步控制系统的鲁棒性,系统进入稳态后,在0.009 s处对3个同步系统的电机3均施加一矩形波干扰,如图6(a)、图7(a)和图8(a)所示。为了便于对3个同步系统进行对比分析,采用重叠绘图的方法,将不同系统的同一种同步误差绘制在一张图中,以电机1和电机3间的同步误差为例,将图6(c)、图7(c)和图8(c)绘制于一张图中,如图9所示。
由图6可知,偏差耦合结构与PID算法相结合的系统中,0~0.002 s内系统处于启动阶段,4电机间的同步误差相对较大且剧烈变化,0.002 s以后系统开始进入稳态,在初期同步误差较大,随着时间的推移,同步误差逐渐减小并趋于零。0.009 s时系统受到扰动作用,电机1和3间的同步误差发生明显的变化,电机1与2、4间的同步误差发生小幅变化。

图6 偏差耦合结构下4电机间的同步误差Fig.6 Synchronization error of relative cross-coupling
由图7结合图9可以看出,相邻交叉耦合结构与PID算法相结合的系统中,同步误差振荡次数比偏差耦合结构的少,这说明偏差耦合控制结构对电机间的同步误差更为敏感,相比之下,相邻交叉耦合控制的控制作用要慢一些,同步误差的变化趋势较为稳定。0.009 s时系统受到扰动作用,电机间的同步误差在-0.01%至0.01%范围内变化,持续大约0.002 s,说明该系统抗干扰的能力不强。

图7 相邻交叉耦合结构和PI控制下4电机间的同步误差Fig.7 Synchronization error of adjacent cross-coupling and PI
由图8结合图9可知,相邻交叉耦合结构与变结构算法相结合的系统中,0~0.004 s内系统处于启动阶段,4电机间的同步误差明显小于偏差耦合结构且变化平缓,0.004 s以后系统开始进入稳态,在初期的0.002 s时间段内同步误差变化较剧烈,但此期间总体上看,误差幅值均明显小于偏差耦合结构。0.009 s时系统受到扰动作用,电机间的同步误差没有发生变化,体现出强鲁棒性。

图8 相邻交叉耦合结构和变结构控制下4电机间的同步误差Fig.8 Synchronization error of adjacent cross-coupling and variable structure control

图9 3种同步系统中电机1和3间的同步误差Fig.9 Synchronization errors of motor 1 and 3 in three systems
经过比较可以发现,对于大功率随动试验台,相邻交叉耦合结构与变结构算法相结合的系统的同步性能远优于偏差耦合结构与PID算法相结合的系统。
7 结论
对于大功率随动试验台中多台永磁同步电机的同步控制问题,由仿真实验和分析可以得到:
1)相邻交叉耦合结构结合滑模变结构方法的同步控制策略,其同步性能优于偏差耦合结构结合PID方法的同步控制策略,同步误差变小,同时系统的鲁棒性变强;
2)相邻交叉耦合比偏差耦合同步控制结构更为简单,并且适宜进行子系统扩展,系统开放性增强,有很好的工程应用前景。
[1] DU H,WEI J H.Motion synchronization control of four multistage cylinders electro-hydraulic elevating system[C]//2010 International Conference on Mechanic Automation and Control Engineering,June 26 -28,2010,Wuhan,China.2010:5249 -5253.
[2] YORAM K.Cross-coupled biaxial computer control for manufacturing systems[J].ASME Journal of Dynamic Systems,Measurement and Control,1980,102(4):265-272.
[3] PEREZ-PINAL F J,CALDERON G,ARAUJO-VARGAS I.Relative coupling strategy[C]//IEEE International Electric Machines and Drives Conference,June 1-4,2003,Madison,USA.2003:1162-1166.
[4] SUN D,SHAO X Y,FENG G.A model-free cross-coupled control for position synchronization of multi-axis motions:theory and experiments[J].IEEE Transactions on Control Systems Technology,2007,15(2):306-314.
[5] 张承慧,石庆升,程金.一种基于相邻耦合误差的多电机同步控制策略[J].中国电机工程学报,2007,27(15):59-63.
ZHANG Chenghui,SHI Qingsheng,CHENG Jin.Synchronization control strategy in multi-motor systems based on the adjacent cou-pling error[J].Proceedings of the CSEE,2007,27(15):59-63.
[6] LI S H,GU H.Fuzzy adaptive internal model control schemes for PMSM speed-regulation system[J].IEEE Transactions on Industrial Informatics,2012,8(4):767 -779.
[7] KULKARNI P K,SRINIVASAN K.Optimal contouring control of multi-axial feed drive servomechanisms[J].ASME Journal of Engineering for Industry,1989,111(2):140-148.
[8] 刘晓峰,刘昕晖,王龙山,等.基于模糊PID控制的大型履带起重机双马达速度同步控制[J].吉林大学学报:工学版,2011,41(3):659-664.
LIU Xiaofeng,LIU Xinhui,WANG Longshan.Speed synchronization control of dual-motor in large crawler crane based on fuzzy PID control[J].Journal of Jilin University:Engineering and Technology Edition,2011,41(3):659-664.
[9] TOMIZUKA M,KAMANO T,HU J S,et al.Synchronization of two motion control axes under adaptive feedforward control[J].ASME Journal of Dynamic Systems,Measurement and Control,1992,114(2):196 -203.
[10] 曹玲芝,李春文,牛超,等.基于相邻交叉耦合的多感应电机滑模同步控制[J].电机与控制学报,2008,12(5):586-592.
CAO Lingzhi,LI Chunwen,NIU Chao,et al.Synchronized sliding-mode control for multi-induction motors based on adjacent cross-coupling[J].Electric Machines and Control,2008,12(5):586-592.
[11] PENG W F,ZHAO D Z.Speed synchronization of multi induction motors with total sliding mode control[C]//2010 Asia-Pacific Power and Energy Engineering Conference,March 28 - 31,2010,Chengdu,China.2010:1-9.
[12] FOO G,RAHMAN M F.Sensorless sliding-mode MTPA control of an IPM synchronous motor drive using a sliding-mode observer and HF signal injection[J].IEEE Transactions on Industrial E-lectronics,2010,57(4):1270 -1278.
[13] ZHANG B T,PI Y G.Enhanced sliding-mode control for permanent magnet synchronous motor servo drive[C]//2011 Chinese Control and Decision Conference,May 23 -25,2011,Mianyang,China.2011:122 -126.
[14] 金宁治,王旭东,李文娟.电动汽车PMSM MTPA控制系统滑模速度控制[J].电机与控制学报,2011,15(8):52-58.
JIN Ningzhi,WANG Xudong,LI Wenjuan.Sliding mode speed control of PMSM MTPA control system for electrical vehicles[J].Electric Machines and Control,2011,15(8):52 -58.

