一种低硬件资源消耗快速SVPWM算法
齐昕, 王冲, 周晓敏, 丛隽, 马祥华, 王长松
(北京科技大学机械工程学院,北京100083)
0 引言
自从电机控制领域引入磁通轨迹控制思想以来,空间矢量调制技术(SVPWM)就开始在该领域被广泛应用。空间矢量调制技术以三相对称正弦电压产生的圆形磁链为基准,通过逆变器开关的不同组合来产生不同的电压矢量,使得实际磁链逼近圆形磁链轨迹[1-2]。近年来,一些学者将研究重心放在多相多电平SVPWM技术在整流器和逆变器上的应用上,文献[3]将SVPWM技术应用在5相逆变器上,文献[4]则进行了六半桥三相SVPWM控制技术的研究。一些学者着重研究SVPWM技术在FPGA、DSP等数字平台上的具体实现[6-9];西南交通大学的王奔教授在文献[7]中提出的基于FPGA的SVPWM发生器的设计;Bowes教授在文献[8]中将SVPWM技术应用在DSP上;东南大学的郑飞博士提出了一种将空间矢量的正六边形细分成48边形的逼近方法并提出了简化方案[10]。德国学者Krah教授和Holtz教授则将研究重点放在SVPWM算法的优化上,在文献[11]中提出了一种确定基础电压矢量作用时间的新方法,能够有效降低运算量。但并未针对基础矢量的切换顺序以及占空比计算等问题作更为具体的研究。
本文在前人的研究基础上,针对双边对称7段SVPWM的特点,将扇区判断进一步优化,提出了简明扇区判据,将判断步骤减少至2次,降低了运算量。同时,不再计算基础电压矢量的作用时间,而是直接计算三相PWM信号的占空比,通过目标矢量在α、β轴分量就可以确定双边对称7段SVPWM合成所需的全部参数。该算法简化了常规算法的运算步骤和运算周期,减少了程序代码,节约了微控制器的内存空间,使SVPWM应用成本进一步降低,促进了SVPWM技术在更低端成本平台的应用。
同时,本文将快速 SVPWM算法在Matlab/SIMULINK中进行了仿真,证明了该快速算法的可行,最后将其应用在以TMS320F28335为控制核心的永磁同步电机变频调速实验中,并给出了实验结果。
1 常规SVPWM算法
1.1 SVPWM核心思想
三相逆变器的电路拓扑结构如图1所示,逆变器可行的开关组合只有8个。

图1 三相逆变器电路拓扑结构Fig.1 Three-phase inverter circuit topology
能够在电机内部产生7种不同的基础电压矢量,如图2所示,6个非零矢量和2个零矢量将一个正六边形平分成6个扇区。

图2 基础电压矢量以及扇区分布Fig.2 The distribution of base voltage vector and sectors
SVPWM的核心思想是使用目标电压矢量所在扇区的基础电压矢量去合成目标电压矢量,通过将向两个基础电压矢量的方向进行投影获得两个基础电压矢量的作用时间。如图3所示,以I扇区为例在正交坐标系α-β系下的两个分量为,,在方向上投影得到的分量为。

图3 目标电压矢量u⇀*位于I扇区Fig.3 Target voltage vector u⇀*in the I sector
由图3可推导出


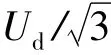


各个矢量作用时间的比例由式(5)计算:

1.2 三相PWM信号的占空比计算
由于最终要对逆变器的开关元件进行控制,需要计算三相PWM信号的占空比,以便设定DSP等微控制器比较寄存器的比较值。

电压矢量切换次序、三相PWM信号以及计数器比较寄存器的数值三者间的关系如图4所示:PWM周期为T,对应计数最大值,记为PRD;在前半个周期的作用时间为t1/2、t2/2,和作用时间均为(T-t1-t2)/4;逆变器ABC三相上桥器件的PWM控制信号分别如图4中红绿蓝三条曲线所示,矢量切换所对应的计数器比较值分别为CMPR1、CMPR2、CMPR3。

图4 I扇区下三相PWM信号的占空比Fig.4 Three-phase PWM signal in the sector I
依据三角形相似原理,有

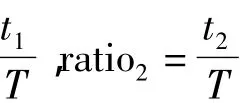

式中,ratio1,ratio2由式(5)计算。

将(1-ratiox-ratioy)/2,(1+ratiox-ratioy)/2,(1+ratiox+ratioy)/2 分别记作 dl,dm,dh,不同扇区下 3个比值按照表1来计算,其中角标x,y∈1,…,6对应基础电压矢量的序号,取值规则亦见表1。

图5 II扇区下三相PWM信号的占空比Fig.5 Three-phase PWM signal in the sector II

表1 各扇区占空比对应表Table 1 The duty ratio of each sector
1.3 基于三相坐标变换的扇区判据
为了计算相邻基础电压矢量作用的时间以及PWM信号对应的3个比值,需要正确判断所在的扇区,常规算法通常使用基于三相坐标变换的扇区判据,利用式(15)将α-β系下的变换到一个特殊的三相坐标系a'-b'-c'系下,两个坐标系的相对位置如图6所示。


图6 a′-b′-c′系与α-β系的相对位置关系Fig.6 The relative position between a′-b′-c′system and α-β system
进而利用u⇀*在a'-b'-c'系下的3个分量ua′ub′uc′以及式(16)来计算所在的扇区。

式中:若 ua′>0,则 p=1,否则 p=0;若 ub′>0,则 q=1,否则 q=0;若 uc′>0,则 r=1,否则 r=0;S 为所在扇区编号。
2 快速SVPWM算法
2.1 压缩变换


图7 压缩变换后的基础电压矢量Fig.7 Basic voltage vector by compressed transform
2.2 基础电压矢量作用时间比的计算
将式(17)代入式(5)可以得到

对比式(5)可以发现,基础电压矢量的作用时间比能够由目标电压矢量压缩变换后的两个分量直接计算,参与的运算只有加减运算,不再涉及浮点数的乘法。
对于其他扇区,则可以利用坐标变换因子e-j(S-1)π/3将变换到I扇区再经压缩变换以及式(17)计算。可设临时变量X,Y,Z为

各个扇区的基础电压矢量作用时间可由表2表示,其中a,b为各个扇区对应基础电压矢量的序号。
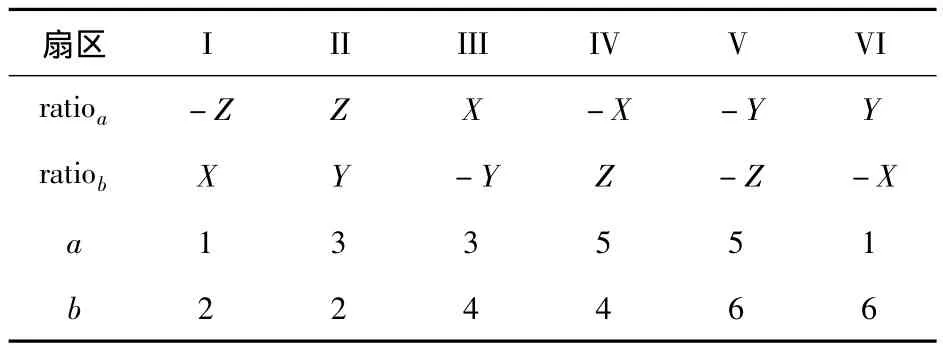
表2 基础电压矢量作用时间表Table 2 The operate time of basic voltage vector
2.3 快速扇区判据
常规算法中需要按照式(15)先将电压矢量u⇀变换到三相坐标系中,之后还要利用其3个分量的符号确定过程变量,最终才能通过式(16)计算出所在扇区,过程十分繁琐。

图8 基于压缩变换的快速扇区判断流程Fig.8 Fast sector judgment process based on compressed transform
任意电压矢量u⇀经过压缩变换后变为u⇀′,其两个分量分别为 u′α,u′β,若 u′β≥0 则意味着矢量位于I、II、III扇区,之后判断 u′α的符号,若 u′α≥0 则意味着矢量位于 I、II扇区,由于 u′α、u′β均为正,故若u′α≥u′β则意味矢量位于 I扇区,否则位于 II扇区,其他扇区同理可得。
对比常规方法,快速判据无需进行三相坐标变换,也无需由公式计算所在扇区编号,能够通过u′α、u′β的符号和大小直接判定电压矢量所在的扇区,有效降低了运算量提高了系统的实时性。
2.4 PWM信号占空比计算
综合表2、表1可以获得不同扇区下三相PWM信号的占空比计算公式,同时对比计算结果发现,I、IV扇区,II、V 扇区,III、VI扇区占空比的计算公式分别相同,因此电压矢量对应的PWM占空比由式(20)~式(22)计算:
电压矢量位于I、IV扇区:

电压矢量位于II、V扇区

电压矢量位于III、VI扇区

2.5 简明扇区判据的提出
如图9所示占空比计算结果相同扇区有3组,无须按照图8判断电压矢量具体位于哪一个扇区,只需要判断矢量属于上述3组中哪一组即可,即判断矢量位于 I、IV扇区或是 II、V扇区亦或 III、VI扇区。

图9 扇区分组Fig.9 The sector group
针对这一特点提出了简明扇区判断,如图10所示。若|u′β|≥|u′α|意味着 β 轴投影分量大于 α 轴投影分量,矢量位于II、V扇区,反之则意味着矢量位于其余4个扇区,且由于I、IV扇区(III、VI扇区)关于原点对称,故可以利用 u′α、u′β是否同号来判定矢量位置。

图10 简明扇区判据Fig.10 Concise sector judgment
对比图10和图8可以发现,快速判据需要三层判断,而简明判据只需要进行两次判断,因此简明判据缩短了算法的代码长度,再次减少了运算量。
最终,可以基于压缩变换的快速SVPWM算法计算流程如图11所示。
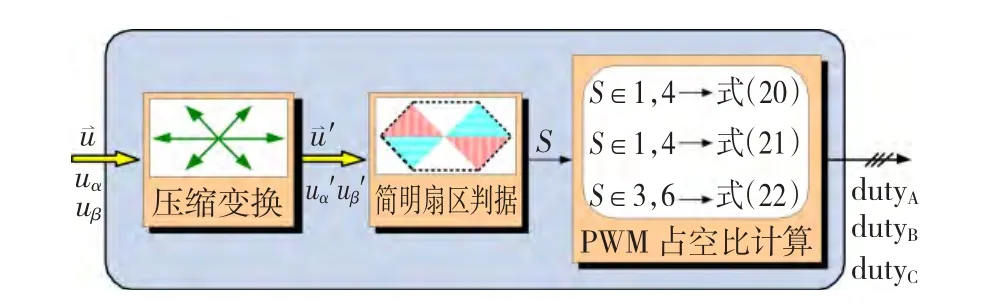
图11 基于压缩变换的快速SVPWM算法Fig.11 Fast SVPWM algorithm based on compressed transform
对比图11与常规SVPWM算法流程图12,可以明显的看到SVPWM快速算法在计算步骤上的优势,它经过压缩变换和简明扇区判断,将原本需要多个计算公式和运算步骤的判断过程集成到了一个简单的判断逻辑下,节省了运算步骤和微控制器的内存空间。

图12 常规SVPWM算法Fig.12 SVPWM conventional SVPWM algorithm
3 快速SVPWM算法的仿真测试
本文使用SIMUINK软件对快速SVPWM算法的可行性进行了仿真测试,仿真系统结构如图13所示,目标电压矢量u⇀*以恒定的幅值和角频率在空间旋转,用以模拟电机运行在稳态时的情况,每个采样周期将生成的u⇀*送入快速SVPWM算法模块进行运算,获得三相占空比,其波形为三相调制波dutyA,dutyB,dutyC,再由PWM驱动模块模拟DSP内部硬件结构生成6路PWM信号,并最终完成对虚拟逆变器的控制。

图13 simulink仿真逻辑图Fig.13 Schematic diagram of system simulation
三相调制波仿真结果如图14所示,波形均为规则的鞍形波,周期与u⇀*旋转的周期相同。图15为快速SVPWM生成的三相PWM信号,信号与常规算法完全一致,证明了此种方法的可行性。

图14 三相调制波波形Fig.14 Three-phase modulation waveform

图15 三相PWM信号Fig.15 Fast SVPWM waveform
4 快速SVPWM算法的实验验证
如图16所示,永磁同步电机变频调速实验模型采用经典的双闭环isd=0控制。系统参数经过控制器调解后得到目标电压矢量u⇀*,再使用快速SVPWM算法输出控制逆变器的6路PWM信号。
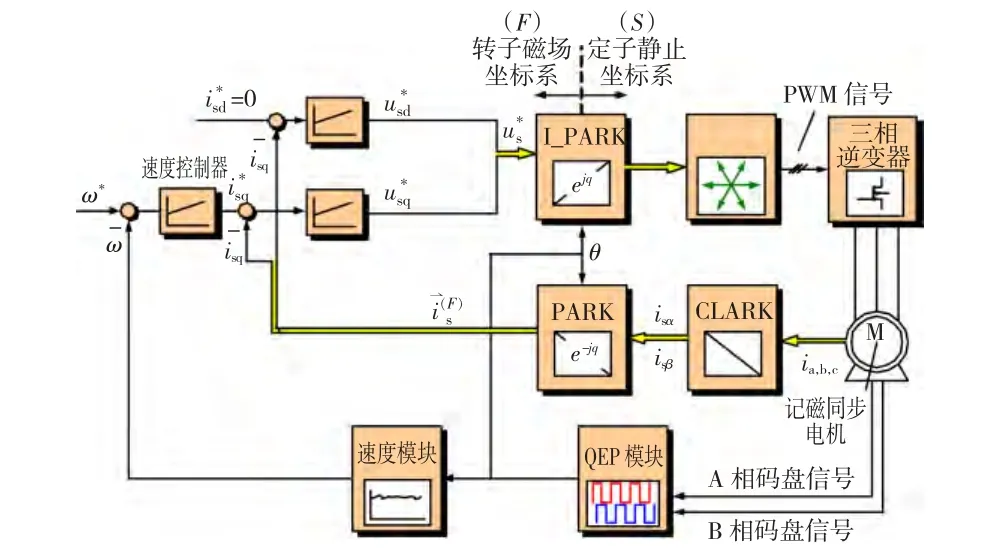
图16 变频调速实验原理图Fig.16 Schematic diagram of Frequency conversion speed regulation experiment
实验平台由TI公司的MDSHVMTRPFCKIT电机控制套件、永磁同步电机、DSP(TMS320F28335)核心控制器、示波器组成,图17为实验平台的实物照片。

图17 硬件实验平台Fig.17 Laboratory equipment platform
在相同的实验条件下分别对常规算法和快速SVPWM算法进行了实验,单相电压如图18所示,通过对比发现使用两种算法得到的单相电压完全一致。
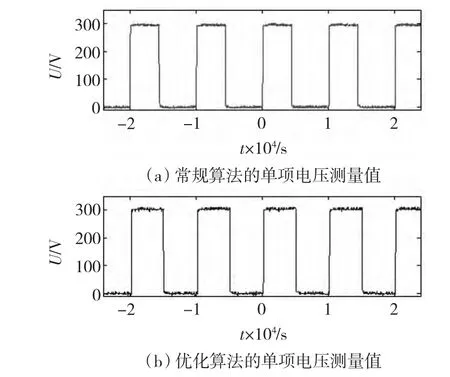
图18 单项电压值Fig.18 Single phase voltage
利用示波器对DSP输出的PWM信号进行了观测,两种方法的实验结果如图19和图20所示。

图19 常规算法生成的PWM波形Fig.19 Conventional SVPWM waveform
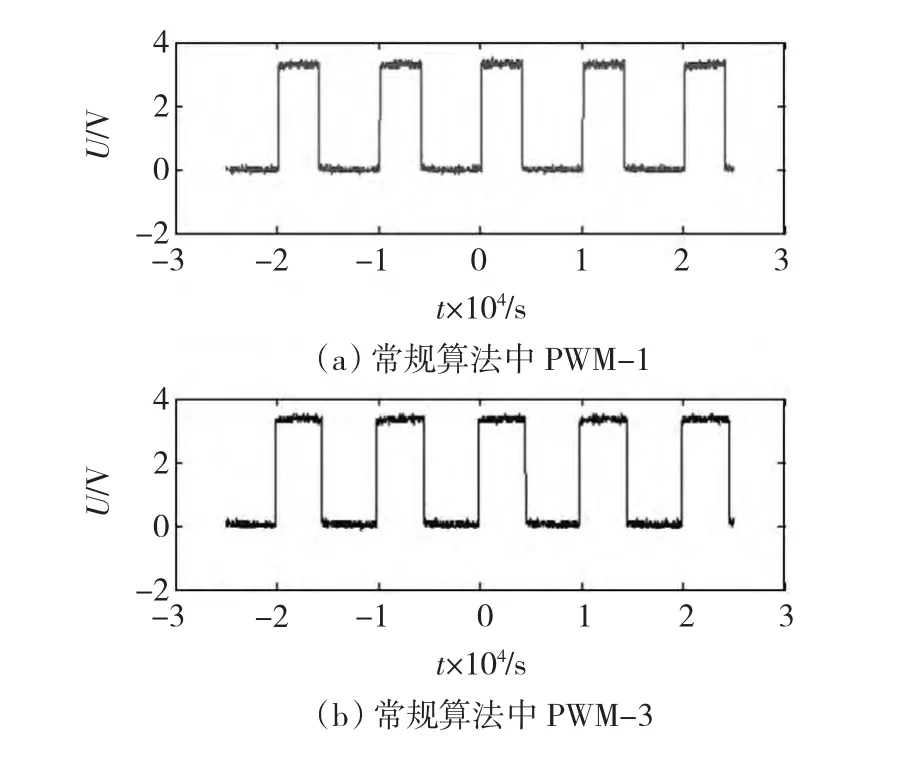
图20 快速算法生成的PWM波形Fig.20 Fast SVPWM waveform
电机运行在 900 r/min、1 800 r/min、3 000 r/min时快速SVPWM算法的调制波波形如图21~图23所示。所以在低速、中速、高速的情况下调制波均能保持规则的马鞍形,证明新算法在全速度范围内都能正常工作。

图21 转速900 r/min时快速算法调制波波形Fig.21 Fast SVPWM modulation waveform at 900 r/min

图22 转速1 800 r/min时调制波波形Fig.22 Fast SVPWM modulation waveform at 1 800 r/min

图23 转速3 000 r/min时快速算法调制波波形Fig.23 Fast SVPWM modulation waveform at 3 000 r/min
通过TI专用的CCS5编译环境对常规SVPWM算法和优化 SVPWM算法进行编译,并在TMS320F28335控制器上运行,常规算法的运算周期为142而优化算法的运算周期为88。从代码大小来看,常规SVPWM算法的代码段大小为256字节,而快速SVPWM算法的代码段大小仅为211字节。
5 小结
本文提出了一种SVPWM的快速算法。通过对空间电压矢量的压缩变换和简明判据,使SVPWM的计算量大大降低。通过Matlab/SIMULINK仿真证明了该算法的正确性,并且将其成功应用在永磁同步电机变频调速实验中。与传统算法相比,该算法由于减少了浮点数的乘法运算、精简了运算步骤,对于TMS320F28335控制器,运算速度提高了38%;编程代码更为节简,共节省了45个字节的内存空间。可见该算法降低了SVPWM算法的硬件资源消耗,具有良好的应用前景。
[1] Ashwin M.Khambadkone,Joachim Holtz.Compensated synchronous PI current controller in overmodulation range and six-step operation of space-vector-modulation-based vector-controlled drives[J].IEEE Transactions on Industrial Electronic,2002,49(3):574-580.
[2] 田亚菲,何继爱,黄智武.电压空间矢量脉宽调制(SVPWM)算法仿真实现及分析[J].电力系统及其自动化学报,2004,16(4):68-71.
TIAN Yafei,HE Jiai,HUANG Zhiwu.Simulation and analyzation of space vector PWM[J].Proceedings of the CSU-EPSA,2004,16(4):68-71.
[3] 李明勇,朱鹏,蔡巍.基于空间矢量脉宽调制的5相H桥型逆变器谐波控制[J].高电压技术,2012,38(11):3080 -3086.
LI MingYong,ZHU Peng,CAI Wei.Harmonics control for fivephase h-bridge inverter based on SVPWM[J].High Voltage Engineering,2012,38(11):3080 -3086.
[4] 宋春伟,赵荣祥.六半桥三相SVPWM控制技术[J].电机与控制学报,2012,16(10).44 -49.
SONG Chunwei,ZHAO Rongxiang,ZHU Minglei.Six half-bridge three-phase SVPWM control technology[J].Electric Machines and Control,2012,16(10).44 -49.
[5] 姚志垒,肖岚.三相SVPWM并网逆变器的改进解耦控制方法[J].电力系统自动化,2012,36(20):99-102.
YAO Zhilei,XIAO Lan.An Improved decoupling control method for three-phase grid-connected inverters with SVPWM[J].Automation of Electric Power Systems,2012,36(20):99 -102.
[6] 陈栋,刘振兴.SVPWM整流器IGBT模块的故障诊断技术研究[J].华北电力大学学报,2012,39(4):72-76.
CHEN Dong,LIU Zhenxing.Fault diagnosis of IGBT,odules for SVPWM rectifier[J].Journal of North China Electric Power University,2012,39(4):72 -76.
[7] WANG Ben,QIU Lebin,Design of SVPWM generator based On FPGA[J].Electric Power Automation Equipment,2012,32(2):56-60.
[8] Sidney R B,Lai Yen-Shin.Shin.The relationship between spacevector modulation and regular-sampled PWM[J].IEEE Transactions on Industrial Electronics,1997,44(5):670 -679.
[9] ZHENG L B,FLETCHER J E.Dual plane vector control of a fivephase induction machine for an improved flux pattern[J].IEEE Transactions on Industrial Electronics,2008,55(5):1996-2005.
[10] 张全川,李文.基于DSP的空间矢量PWM波实现[J].电力电子技术,2007,41(12):90-92.
ZHANG Quanchuan,LI Wen.Realization of Space Vector PWM based on DSP[J].Power Electronics,2007,41(12):90 -92.
[11] J.Holtz,Jens-Onno Krah,High-performance current regulation and efficient PWM implementation for low inductance servo motors[J].IEEE Transactions on Industry Applications,1999,35(5):1039-1049.
[12] 杨贵杰,孙力.空间矢量脉宽调制方法的研究[J].中国电机工程学报,2001,21(5):79-83.
YANG Guijie,SUN Li.Study on method of the space vector PWM[J].Proceedings of the CSEE,2001,21(5):79 -83.
[13] 李峰.矢量控制系统中优化PWM控制策略的研究[D].天津大学,2003.
[14] 祝琴,钟祥微,章鸿.SVPWM 原理及其 Simulink仿真[J].电机电器技术,2005(4):49-51.
ZHU Oin,ZHONG Xiangwei,ZHANG Hong.The principle of SVPWM and simulation in simulink[J].Electric Motor Technology,2005(4):49-51.
[15] 杨大柱.感应电机SVPWM控制系统的仿真研究电机技术[J].现代驱动与控制,2009(5):32-34.
YANG Dazhu.Simulation study of SVPWM control system of induction machine[J].Modern Drive and Control,2009(5):32 -34.

