统一电能质量控制器并联侧的改进双滞环电流控制策略研究
程启明, 陈根, 程尹曼, 李明, 王鹤霖
(1.上海电力学院 自动化工程学院,上海200090;2.上海电力公司市北供电分公司,上海200041)
0 引言
目前大量以电力电子装置为代表的非线性负荷投入运行,对电网造成谐波污染,这使得电能质量问题日趋严重。统一电能质量调节器(unified power quality controller,UPQC)是一种改善电能质量的有效手段,它将串联与并联的有源电力滤波器(active power filter,APF)组合起来,改变了传统电能质量治理中电压与电流分别补偿的方法,能够整体上同时补偿系统电流与电压,因而受到了广泛的关注[1-3]。
在目前的UPQC控制策略中,一般的做法是UPQC串联补偿单元控制为电压源来补偿电网基波电压和谐波电压,并联补偿单元则被控制为电流源来吸收负载谐波电流。而并联APF实现电流补偿很大程度上取决于逆变器采用的电流控制方法。目前电流跟踪控制方法有很多,最常用的是滞环电流控制方法[4-6]。这种方法可以获得较好的控制性能,精确度较高且响应快,但由于三相滞环是各自独立的为未考虑相间影响,缺乏协调可能引起较大的开关噪声和电流脉动[7-9]。本文采用一种基于电压空间矢量的双滞环电流控制技术,该方法根据误差电流的区域而选取不同的电压矢量来控制逆变器输出电流,使误差电流处于复平面的内环之中,从而使APF 输出电流实时跟踪指令电流[10-15]。
在常规的双滞环控制中,当误差电流在内环时不受控制,逆变器开关不动作,这样就降低了UPQC的补偿精确度,不能有效抑制谐波。本文采用了一种改进的双滞环控制方法,当误差电流在内环时,引入了自抗扰控制器(active disturbance rejection controller,ARDC),它将负载电流和电源电压等因素作为系统的未知干扰,再通过扩张状态观测器(extended state observer,ESO)来估计,最后利用非线性反馈控制律(nonlinear states error feedback,NLSEF)进行补偿[16-18]。由于ADRC中需要整定的参数众多,所以ADRC估计外部扰动和跟踪电流参考信号受到了一定的限制。因此,本文采用混沌粒子群算法对ADRC参数进行整定及优化。这种方法不仅提高了电压效率,降低了开关频率,减少系统损耗,还能有较好的电流响应速度和补偿精确度,又能有效限制误差电流[19-22],并且对不同的负载和电流的变化有很强的适应性。Matlab软件仿真和DSP硬件实验验证了本方法的有效性和可行性。
1 UPQC电压空间矢量控制原理
图1为UPQC的基本拓扑结构,UPQC主要由检测和控制及主电路3个部分组成,其中主电路由串联单元、并联单元和直流储能单元构成,串联、并联单元分别负责电压、电流的谐波补偿;检测部分是从补偿对象的电路中提取电压和电流谐波以及无功分量等补偿量;控制部分根据检测部分得出的补偿量作为参考信号,控制开关器件的通断,使主电路输出符合要求的电压和电流。

图1 UPQC的拓扑结构Fig.1 The topological structure of UPQC
为实现双滞环内环自抗扰控制,只讨论UPQC并联单元系统。
图2为并联单元系统的单相(A、B、C三相中一相)等效电路。图中,us为电网电压,iL为负载电流,Ls为电网平波电感,Rs为电网电阻,R为注入电阻,L为注入电感,C为直流侧电容,Uc为直流侧电容电压。

图2 UPQC并联单元系统的单相等效电路Fig.2 The single phase equivalent circuit of the shunt APF of UPQC
根据基尔霍夫电压定律,可得系统的单相瞬时电压方程为

式中:ucx为UPQC并联单元逆变器的输出电压;icx为补偿电流;uix为并联点电压;x表示A、B、C三相。
设三相系统对称,引入开关函数 SA、SB、SC,则三相逆变器相应的输出电压又可表示为[3]

由式(2)可知,每相输出电压都同时与三相桥臂的总体状态相关,即三相桥臂之间存在相互干扰。为了消除相间影响,把静止ABC坐标转换到静止αβ坐标系[5]。当α轴与A轴重合时,两坐标系的变换关系为

由式(3)可知,对应不同的[SA,SB,SC]开关矢量,uA,uB,uC相应的电压空间矢量可方便地表示为αβ 平面中的一个复数[6],即

式中,u(k),k=0,1,…,7 为 8 种电压空间矢量。
由式(1)可得UPQC并联侧输出端电压矢量方程式为

式中:uc,ic,ui分别为(ucA,ucB,ucC),(icA,icB,icC),(uiA,uiB,uiC)对应的空间矢量。

定义电流误差矢量Δi为

由式(5)和式(6)相减可得

式中,忽略了交流侧的电阻,并且为了跟空间电压矢量相对应,令uc=uk。由式(8)可知,误差电流矢量Δi的变化率取决于参考电压矢量与输出电压矢量uk的偏差。
在传统单滞环控制法中,当di*/dt较大时,因所选的uk对应的矢量dΔi/dt的模值较小,即Δi变化较慢,无法使矢量ic快速跟踪变化较快的矢量。所以,对于已判断出所在区域的参考电压矢量,只要适当选择输出的电压矢量uk,就可以控制电流误差矢量 Δi的变化率 dΔi/dt,从而控制电流误差矢量 Δi[8]。
2 基于电压空间矢量的双滞环电流控制方法
图3为Δi区域分布图。图中相间误差电流Δi所在区域被分为两个滞环宽度和12个区域。其中外环、内环宽度分别为hM、hm(hm<hM)。

图3 最佳电压矢量的判定图Fig.3 The space distribution of Δi
1)当Δi处在外环时(|Δi|>hM),即实际电流出现较大误差时,首先治理误差绝对值最大的相,使Δi迅速减小。这时应立即选取该区域轴线方向上的最佳电压空间矢量u(k)(k=1,2,…,7),因为不论此时参考电压在哪个区域,都能找到一个uk沿Δi反方向的最大分量迫使Δi迅速减小,且速率最大。

表1 外环uk选择表Table 1 The select table of uk
2)当 Δi处于双环之间时(hm< |Δi|<hM),应采取更精确、稳定的控制策略。根据Δi和u各自所处的区域,选取一个最佳电压空间矢量uk与Δi方向相反,且幅值最小,从而使Δi减小缓慢,以达到减少开关次数和降低高次谐波含量的目的。

表2 双环之间uk选择表Table 2 The select table of uk
3 内环的ADRC控制策略
当Δi处于内环时(|Δi|<hm),常规的双滞环控制开关不动作,这会导致UPQC并联单元谐波电流补偿精确度降低,而本文提出的改进方法是在内环时将负载电流和电源电压等因素作为系统的未知干扰设计自抗扰控制器(ADRC)[16]。
3.1 自抗扰控制器的设计
由图2分析可得

式中,uc1=mUc,m为PWM调制量。
电源电压和负载电流的波动可以看作是系统的未知干扰,联立式(9)和式(10)可得

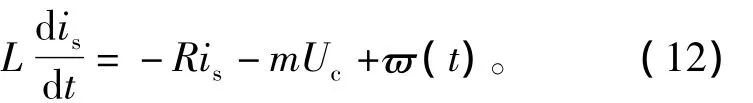
ADRC的综合扰动项a(t)、常数项b分别定义为

这样,式(12)可表示为

图4为误差电流内环采用ADRC控制系统的结构。图中,TD为跟踪微分器,它产生一个参考输入的跟踪信号 z,对参考信号起到一种柔化作1用[17]。其表达式为


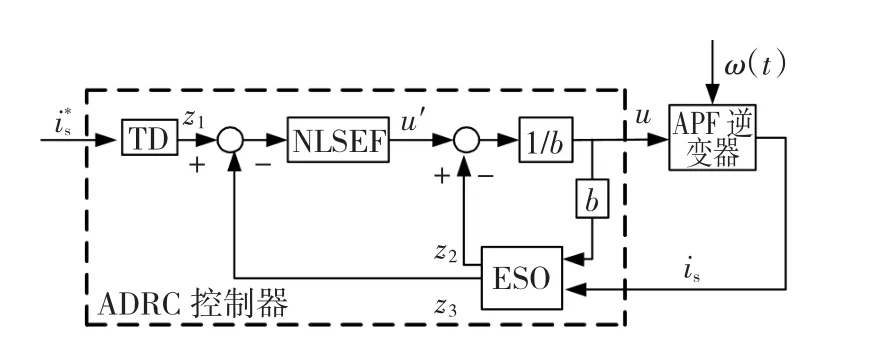
图4 自抗扰控制系统的结构Fig.4 The structure of ADRC control system
ESO为二阶扩张状态观测器,它是由对象输出和对象总扰动的实时作用量(对象所有不确定模型和外扰作用的总和),其输出为z2、z3两个信号,其中z3为is的跟踪信号,z2为对系统模型和外扰动(总扰动)的估计,而z2/b起补偿扰动的作用。

对TD和ESO进行分析可知,z1是安排的过渡过程,而z3相当于对象的状态变量,令ξ=z1-z3为这两组变量之间的误差,即对象跟踪参考输入i*s的状态误差[18]。这些误差的非线性组合(NLSEF)和总扰动估计量的补偿分量z2/b可用来生成控制信号u。

系统的总输出为

由式(19)可知,系统的控制律与系统内部的参数和未知扰动无关,而只是与系统的输出和给定输入有关[16]。
3.2 混沌粒子群算法参数优化
ADRC控制性能主要取决于其控制参数的合理选取。在跟踪微分器中r是加速度参数,它决定了z1在任意有限时间内充分逼近输入信号的的跟踪速度。而对系统模型和外扰动的估计以及非线性状态反馈对总扰动估计量的补偿则取决于β01,β02,β03的合理选取。本文主要选这4个参数为优化参量。
在粒子群算法中,参数优化问题被抽象为没有质量和体积的粒子,并延伸到4维空间[19]。假设4维搜索空间第i个粒子在空间中的位置和速度分别用 Xi=(xi1,xi2,…,xin)和 Vi=(vi1,vi2,…,vin)来表示,第i个粒子的本身所找到的最优位置为Pi=(pi1,pi2,…,pin),整个粒子群的全局最优位置 Pg=(pg1,pg2,…,pgn)。每个粒子的速度以及位置按式(20)迭代更新[19],即
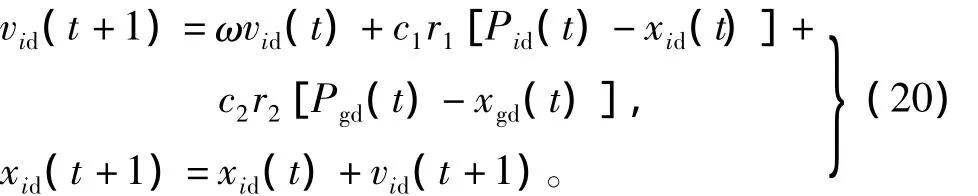
式中:c1、c2为加速因子,且为正实数;r1,r2为[0,1]间的随机数;ω代表惯性因子。
ω的自适应权重取法公式为

式中:ωmax、ωmin分别为最大、最小惯性权值;f1为粒子当前的目标函数值;favg、fmin分别为当前所有粒子的平均目标值、最小目标值。
针对粒子群算法容易陷入局部极小值,出现早熟收敛现象的问题。本文将混沌优化和粒子群算法结合,当粒子限于局部最优解时,采取混沌序列的搜索算法来完成对受惩罚粒子重新搜索,使其尽快逼近到全局最优解[20]。
混沌局部搜索算法选择Logistic方程来进行混沌变量的迭代,即

式中:sj(k)是混沌变量;μ是控制参量,当μ=4时,式(22)完全处于混沌状态且混沌变量sj在(0,1)范围内遍历。混沌粒子群算法步骤为:
1)随机初始化每个粒子的位置和速度。
2)将各微粒的位置和适应值存储在各微粒的pbest中,将所有pbest中最优个体的位置和适应值存储在gbest中。
3)计算各微粒的目标函数值,然后保留群体中性能最好的20%的微粒。
4)将粒子目前全局最优位置pg作为决策变量xj(k),然后按下式映射为0到1之间的混沌变量sj(k),即

式中:k 为迭代次数;xmax,j、xmin,j为第 j维向量的搜索上下界。
5)按式(22)计算出下一步迭代的混沌变量sj(k+1),再将按下式转换为决策变量xj(k+1),即
xj(k+1)=xmin,j+sj(k+1)(xmax,j- xmin,j)。 (24)
6)根据决策变量xj(k)对新解进行评价,若新解优于初始解或已达到最大迭代次数将新解作为搜索结果,并更新pbest和gbest,否则转步骤4)。
7)按收缩搜索区域

式中,xg,j表示pbest当前第j维变量。在收缩后的空间内随机产生群体中剩余的80%的微粒,转步骤2)。
4 UPQC的软件仿真平台实验
利用Matlab/SIMULINK中的电力系统模块SimPowerSystems对UPQC系统进行建模和仿真分析。UPQC可采用基于三相瞬时无功功率理论的ip-iq法来从负荷电流中分离出电压、电流的谐波分量[21-22]。
仿真中,相关参数选取为:电源线电压为380 V/50 Hz;电网电阻 Rs=10 Ω;注入电阻 R=2 Ω;平波电感Ls=2 mH;注入电感L=2 mH;直流侧电压Uc=350 V;直流侧电容C=2 200 μF/450 V;串联侧耦合变压器变比为3:1;内环宽度hm和外环宽度hM约为系统电流峰值的3%和7%。
ADRC的被优化的参数的变化范围和参数取值为:r∈(0,120 000),β01∈(0,100 000),β02∈(0,100 000),β03∈(0,1 000),α1=0.5,δ1=0.001,α0=0.5,δ0=0.000 1,α2=0.45,δ2=0.000 1。混沌PSO 参数设置为:M=40,D=5,T=30,c1=2.0,c2=2.0,k=0.32,ω1=0.78,ω2=100,E=0.05,J1=100 000,ωmin=0.45,ωmax=0.82,ε =0.000 1,Tc=8,Nmax=60,Rd(t)设为各个参数定义域的25%。经过50代进化,获得的 ADRC优化参数为:r=100 125,β01=61 478;β02=72 536;β03=480。
图5为采用单滞环、常规的双滞环及改进的双滞环3种不同方法时开关动作次数的比较曲线。

图5 3种滞环方法开关状态图Fig.5 The state picture of the three hysteresis models
由图5可见,传统双滞环方法比单滞环方法的每相开关次数约减少了12.8%,也就是说开关损耗大约降低了12.8%。由于改进后双滞环方法的内环也将控制,所以它比传统双滞环方法的开关次数增加了约3.6%,但还是比单滞环方法的开关次数减少了9.2%,因此,改进的双滞环方法还是起到了减少开关频率和提高装置安全性的作用。
图6为单滞环、常规的双滞环和内环分别采用PI控制和自抗扰控制的谐波分析图。补偿前电流谐波畸变率为33.59%;UPQC投入补偿后,单滞环和双滞环电网电流谐波畸变率分别为0.72%和0.33%;当内环采用PID方法控制后电网A相电流谐波畸变率降低为0.26%;而ADRC方法的电网电流谐波畸变率是0.02%。

图6 4种情况下谐波分析Fig.6 The harmonic analysis in the four conditions
为验证自抗扰控制器的鲁棒性,以负载扰动作动态仿真实验。仿真结果如图7和图8所示,在0.02 s时刻,负载电流由4.8 A突变到8 A。
从图7和图8中可以看出,当负载突变时,内环PI控制的电网电压和电网电流要满足负载变化的需要都有一点时间的延迟,动态响应比ADRC控制器慢。并且与ADRC方法时相比补偿电流的参考值震荡更大。由此可见,采用文中所提出的控制方法,当负载电流发生突变时,ESO可以快速地估计出这种变化,并将信息反馈给ADRC进行补偿,使补偿电流可以实时精确地跟踪电网的谐波电流。

图7 负载突变时ADRC控制方法仿真曲线Fig.7 The simulative curves of ADRC method at sudden change of load

图8 负载突变时PID控制方法仿真曲线Fig.8 The simulative curves of PID method at sudden change of load
5 UPQC硬件平台实验
在基于DSP的UPQC硬件实验平台上进行实验验证。图9为UPQC硬件结构,它主要由主电路和控制电路两部分组成。主电路主要包括电源电路、IPM智能功率模块、直流侧电容、串联侧的耦合变压器、滤波电路以及负载;而控制电路主要包括以 TMS320LF2407A(或 TMS320F2812等)为核心的控制电路、驱动信号隔离电路、传感器检测电路、检测信号转换与电平偏移电路及供电电源。
UPQC实验软件采用C语言编写,由主程序和两个中断服务子程序组成。主程序主要执行各部分的初始化程序以及分配中断服务的中断向量。一个中断服务子程序是由外部申请中断,执行电压过零点检测的功能。另一个中断服务子程序是由定时器申请中断,在定时器的一个中断周期内,进行数据采集、补偿量检测、产生补偿量等工作。

图9 基于DSP的UPQC硬件结构Fig.9 The block diagram of UPQC hardware structure based on DSP
图10为在UPQC硬件平台上且在平衡电阻负载(每相均为5 Ω)下的三相电网电压及电流波形。由图可见,内环采用ADRC控制方法的电流、电压补偿曲线比较光滑。

图10 UPQC硬件平台上的实验波形Fig.10 The experimental waveforms on the UPQC hardware platform
实验结果验证了本方法的有效性和可行性。
6 结语
本文在传统的基于电压空间矢量双滞环电流控制方法的基础上,针对误差电流处于内环时逆变器不动作导致的补偿精确度降低的问题,提出了一种基于ADRC的混合有源滤波的直接电流控制方法。此法是在对电能质量控制器、电源及非线性负载三者之间的有功功率平衡分析的基础上,将负载电流和电网电压等因素作为系统的未知干扰进行补偿,实现有源电力滤波器的控制。该方法不受负载电流和电网电压的影响,且运算量小、开关频率比单滞环低,从而提高了补偿精确度。最后利用结合混沌优化和粒子群优化算法对控制器各个参数优化。软件仿真与硬件实验结果验证了所提方法的正确性和有效性。
[1] 朱鹏程,李勋,康勇,等.统一电能质量控制器控制策略研究[J].中国电机工程学报,2004,24(8):67-73.
ZHU Pengcheng,LI Xun,KANG Yong,et al.Study of control strategy for a unified power quality conditioner[J].Proceedings of the CSEE,2004,24(8):67-73.
[2] 冯兴田,马文忠,霍群海,等.基于无功功率流的UPQC协调控制策略[J].电机与控制学报,2013,17(4):1-5.
FENG Xingtian,MA Wenzhong,HUO Qunhai.et al.Coordinated control strategy based on reactive power flow in UPQC[J].Electric Machines and Control,2013,17(4):1 -5.
[3] 巫付专,万健如,沈虹.不同补偿策略下UPQC主电路参数确定方法[J].电机与控制学报,2010,14(6):71-76.
WU Fuzhuan,WAN Jianru,SHEN Hong.Parameters determination of UPQC based on different compensation strategies[J].Electric Machines and Control,2010,14(6):71 -76.
[4] 郭自勇,周有庆,刘宏超,等.一种基于电压空间矢量的有源滤波器滞环电流控制新方法[J].中国电机工程学报,2007,27(1):112-117.
GUO Ziyong,ZHOU Youqing,LIU Hongchao,et al.A novel hysteresis current control method for active power filter[J].Proceedings of the CSEE,2007,27(1):112-117.
[5] 张志超,魏富建,王义峰.单周期控制策略在统一电能质量调节器中的应用研究[J].电力系统保护与控制,2009,37(22):28-33.
ZHANG Zhichao,WEI Fujian,WANG Yifeng.Applied research on one-cycle control method of unified power quality conditioner[J].Power System Protection and Control,2009,37(22):28 -33.
[6] 曾国宏,郝荣泰.有源滤波器滞环电流控制的矢量方法[J].电力系统自动化,2003,27(5):31-40.
ZENG Guohong,HAO Rongtai.A novel phase-correlating hysteresis current control method for active power filter[J].Automation of Electric Power Systems,2003,27(5):31 -40.
[7] 汤赐,罗安,赵特,等.新型注入式混合有源滤波器的数学模型及电流控制方法[J].电工技术学报,2008,23(3):72-79.
TANG Ci,LUO An,ZHAO Te,et al.Study on mathematic modeling and current control method of new injection type hybrid active power filter[J].Transactions of China Electro technical Society 2008,23(3):72-79.
[8] JOU H L,WU J C,CHANG Y J,et al.A novel active power filter for harmonic suppression[J].IEEE Transactions on Power Delivery,2005,20(2):1507-1513.
[9] 曾江,刁勤华,倪以信,等.基于最优电压矢量的有源滤波器电流控制新方法[J].电力系统自动化,2000,24(6):25-31.
ZENG Jiang,DIAO Qinhua,NI Yixin,et al.A novel current control method for active power filter based on optimal voltage vector[J].Automation of Electric Power Systems,2000,24(6):25 -31.
[10] 叶小军,曾江,王克英,等.并联有源电力滤波器双滞环电流控制策略[J].电力系统保护与控制,2009,37(9):60-64.
YE Xiaojun,ZENG Jiang,WANG Keying,et al.Double hysteresis current control strategy for shunt active power filter[J].Power System Protection and Control,2009,37(9):60-64.
[11] MAREI M I,EL-SAADANY E F,SALAMA M M A.A new contribution into performance of active power filter utilizing SVM based HCC technique[J].IEEE Power Engineering Society Transmission and distribution conference,July 21 - 25,2002,Chicago,USA.2002,2:1022 -1026.
[12] 王新勇,许炜,汪显博,等.光伏并网逆变器空间电压矢量双滞环电流控制新策略[J].电力系统保护与控制,2011,39(10):110-116.
WANG Xinyong,XU Wei,WANG Xianbo,et al.A novel double hysteresis loop current control method for three-phase PV gridconnected inverter with voltage space vector[J].Power System Protection and Control,2011,39(10):110 -116.
[13] 王群,姚为正,刘进军,等.谐波源与有源电力滤波器的补偿特性[J].中国电机工程学报,2001,21(2):16-20.
WANG Qun,YAO Weizheng,LIU Jinjun,et al.Harmonic source and compensation characteristics of active power filters[J].Proceedings of the CSEE,2001,21(2):16-20.
[14] ZHU Pengcheng,CHEN Jian.The power conversion system performance of a super conducting magnetic energy storage unit[C]//The 4th IEEE International Conference on Power Electronic and Drives and Systems,October 22 -25,2001,Bali,Indonesia.2001:611-617.
[15] WANG Yong,SHEN Songhua.Research on one-cycle control for switching converters[C]//Proceedings of the 5th World Congress on Intelligent Control and Automation,June 15 - 19,2004,Hangzhou,China.2004:74-78.
[16] 许湘莲,邹云屏,郭江.基于自抗扰控制器的级联多电平静态同步补偿器控制系统[J].中国电机工程学报,2007,27(31):40-44.XU Xianglian,ZHAO Yunping,GUO Jiang.Control system of cascade multilevel statcom based on auto-disturbance rejection controller[J].Proceedings of the CSEE,2007,27(31):40-44.
[17] 史伟伟,蒋全,胡敏强,等.串联型电力有源滤波器中低通滤波器的设计及参数优化[J].中国电机工程学报,2003,23(11):74-78.
SHI Weiwei,JIANG Quan,HU Minqiang,et al.Design and optimization of passive low pass filter[J].Proceeding of the CSEE,2003,23(11):74-78.
[18] 黄本润,夏立,吴正国.自抗扰控制器在动态电压恢复器中的应用[J].电机与控制学报,2012,16(6):106-110.
HUANG Benrun,XIA Li,WU Zhengguo.Active disturbance rejection controller for dynamic voltage restorer[J].Electric Machines and Control,2012,16(6):106 -110.
[19] SURESH S,SUJIT P B,RAO A K.Particle swarm optimization approach for multi-objective composite box-beam design[J].Composite Structures,2007,81(4):598 -605.
[20] 张浩,张铁男,沈继红,等.Tent混沌粒子群算法及其在结构优化决策中的应用[J].控制与决策,2008,23(8):857-862.
ZHANG Hao,ZHANG Tienan,SHEN Jihong,et al.Research on decision-makings of structure optimization based on improved Tent PSO[J].Control and Decision,2008,23(8):857 -862.
[21] GHOSH A,IEDWICHh G.A unified power qualiry conditioner(UPQC)for simultaneous voltage and current compensation[J].Electric Power Systems Research,2001,59(1):55-63.
[22] EI-HABROUK M,DARWISHA M K,MEHTA P.Active power filter:a review[J].IEE Proceeding-Electric Power Applications,2000,147(5):403 -410.

