我国股票、债券和期货市场波动溢出效应的实证分析——基于GARCH－BVAR模型

李新光，左硕之（．武夷学院商学院，福建南平 354300；．云南财经大学统计与数学学院，云南昆明 650）

我国股票、债券和期货市场波动溢出效应的实证分析
——基于GARCH－BVAR模型

李新光1，左硕之2
（1．武夷学院商学院，福建南平 354300；2．云南财经大学统计与数学学院，云南昆明 650221）

基于2002年12月－2013年2月股票成交额、期货成交额以及国债成交额等数据资料，运用GARCH（1，1）模型获取各市场的波动信息，通过贝叶斯VAR模型（BVAR）、脉冲响应函数（IRF）等方法模拟各市场波动的“传染”过程，研究发现：第一，股票市场与期货市场均对来自自身冲击影响的反应比较强烈，期货市场的冲击对股票市场的影响较小但是持续时间长，股票市场的冲击对期货市场的影响较弱；第二，股票和期货市场的冲击对国债市场影响在整个样本期间均不大。

贝叶斯向量自回归模型（BVAR）；GARCH模型；期货市场；股票市场；债券市场

一、引 言

股票、债券、期货是证券市场中三大重要组成部分，随着金融全球化的快速发展，各证券市场间联系日渐密切，只要某一领域出现波动，就会快速影响至其他子市场。探讨不同市场在面对外部冲击时如何相互影响和传染，正确引导不同市场健康发展，关系到一个国家金融监管当局金融政策的制定，有助于维护证券市场的稳定、繁荣。为进一步说明不同证券市场之间风险的相互传染路径，促进它们有序协调发展，构建一个涉及股票、债券、期货三者的动态模型来探讨不同市场风险溢出效应，具有一定的理论和现实意义。

我国证券市场之间风险传递的相关问题受到国内学者的广泛关注，取得了一定成果。王宝［1］运用DCC－MVGARCH方法对我国证券市场间风险传染问题进行了分析，发现股票市场和债券市场之间容易传染。蒋序怀等［2］运用VAR模型对传染效应存在的渠道进行了实证研究，发现股票市场与债券市场间的联系较为密切。陈燕武等［3］运用非参数分位数回归，得到中、美、英、日四国股票市场存在非线性的风险传染效应。陈庭强等［4］从银行信贷行为视角对信用风险转移市场信用风险传染的特征、实践路径进行了评述。此外，兰鹏［5］采用BEKK模型，发现中国香港、中国台湾等亚洲6个地区或国家股票市场间风险存在显著的溢出效应。华桂宏等［6］采用三元VAR模型，发现金融发展会主动刺激固定资产投资，银行体系对投资的刺激功能更显著，而股票市场不具备这种功能。张慧莲［7］以上海证券交易市场为例，得出证券投资基金是上证指数的单向granger原因，而上证指数与保险市场之间不存在granger因果关系。

国外学者主要针对不同国家股票市场之间风险传染进行研究，而针对股票与其他市场之间的传染分析较少。比较有代表性的成果有：Theodossiou等［8］采用广义GARCH方法分析了美、日、英等主要发达国家股票市场收益波动特征，发现它们之间存在显著传染效应。King等［9］认为由于资本市场代理人对其他市场价格波动信息的不准确预期，导致错误信息很容易传染至其他市场。Hahm［10］发现美国对韩国的股票市场的滞后波动溢出效应显著，反之则不然；但未发现收益率之间存在相互溢出效应。Park等［11］通过自回归模型研究了亚洲危机期间各金融市场传递情形，结果发现东南亚市场并未直接触发韩国的危机，而台湾金融市场的不稳定是重要原因。

传统的VAR模型不能回避待估参数过多和自由度问题，这可能导致估计可能会出现偏误；同时，还会由于各滞后变量之间可能存在高度的共线性关系导致结果出现一定的偏误。因此，本文尝试从以下几个方面进行分析：一是选择代表不同风险市场的代理变量，对各市场之间风险传递进行分析；二是将克服传统VAR的上述缺陷，运用贝叶斯向量自回归模型（BVAR）进行建模，搜集最新月度数据进行实证，以分析期货、债券、股票市场之间风险的溢出效应。

二、贝叶斯向量自回归模型（BVAR）概述

含有k变量的p阶向量自回归模型VAR（p）的一般矩阵形式可以表示如下：

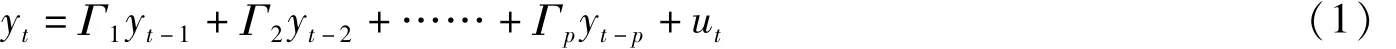
其中，yt是k阶内生变量向量，p是滞后阶数，Γ1、Γ2……Γp是k×k待估计的系数矩阵，ut是扰动向量，而且E（ut）＝0，E（utut′）＝Σ，E（utus′）＝0，t≠s。

虽然VAR模型克服了一般联立方程模型需要严格区分内、外生变量的缺陷，但是它本身亦存在不可避免的缺点［13］：第一，待估参数太多，对时间序列长度要求较大。如果VAR模型中有m个内生变量、滞后阶数为p，则将有m（mp＋1）个参数需要估计。由于我国金融市场可得数据时间跨度不长，将普通VAR模型应用于中国金融市场研究是很不利的。第二，由于普通VAR模型中的解释变量均为被解释变量向量的各阶滞后项组成，如y1t－1，y1t－2，……。这些滞后解释变量容易产生高度的共线性关系，从而导致系数估计偏误。

为此，Litterman［13］和Sims［14］提出通过引入贝叶斯先验信息，可以克服上述问题。根据Sims所提出的方法，设xt＝（yt－1，yt－2，yt－3……yt－p，1），则（1）式可表述为：

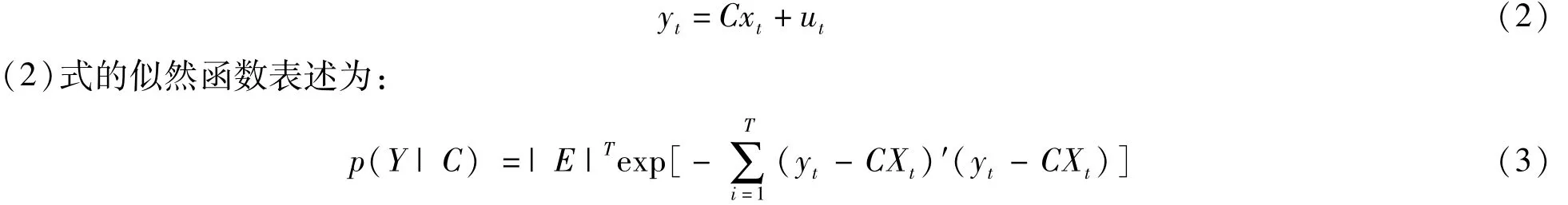
其中，E为单位矩阵。

其中e和c的后验概率密度函数为：

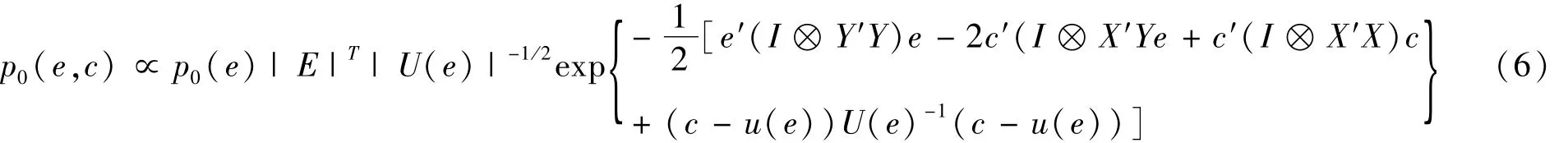
可见，（6）式是关于c的二次方程式，它服从正态分布，可以通过MCMC模拟或其他计量统计方法求得。

三、实证研究

（一）变量选取与数据处理

本文分析指标主要选取股票成交额（gp）、国债成交额（zj）和期货成交额（qh）。其中股票成交额为深交所、上交所股票成交额当月数之和。国债成交额为上交所、深交所国债现货、回购成交额当月数之和。期货成交额为上海、大连、郑州三大商品交易所期货成交额当月数之和。单位为亿元。

为了保证所有数据的完整性、可得性，选取2002年12月－2013年2月的月度数据，共123个样本。数据来自中经网、中国人民银行网站。对所有数据作剔除物价因素，考虑到月度数据可能存在季节影响，对所有指标进行剔除季节①用eviews软件，运用X12方法去除季节性。因素处理。为了缩小指标本身差异和消除可能存在的异方差，对上述经过处理后的指标取对数，分别记作：期货成交额为lnqh；债券成交额为lnzj；股票成交额为lngp。

（二）运用GARCH（1，1）提取各变量“风险”信息

通常在金融市场上是用方差来衡量金融产品收益的风险和价格的不确定性，Engle［15］提出的“自回归条件异方差模型”（Autoregressive Conditional Heteroskedasticity Model）被广泛运用于金融时间序列中。马超群等［16］认为“研究这类具有丛集性与异方差性特征的金融数据变动规律性的最有效方法与途径”。本文借鉴前人的做法，采用GARCH模型中的条件异方差的回归形式来反映出金融市场不确定性，具体用模型残差的条件方差项来模拟各大市场的波动率（即风险信息）。GARCH（1，1）模型可以表述为：

其中，yt为期货、股票、债券等变量，μ、c、α、β为未知参数，它们的值由最大似然法估计。条件方差t是后续在BVAR模型中将用于反映风险的变量（波动率）②在进行GARCH（1，1）分析之前，我们用三个变量lngp、lnqh、lnzj分别对常数进行回归，然后对残差进行ARCH效应检验，lngp与lnqh回归后的残差均在滞后一期resid＾2（－1）的1%水平显著；而lnzj回归后的残差在滞后1－4期均在5%水平下显著。可见，都存在arch效应，可以进行后续的GARCH建模分析。。最后，通过GARCH（1，1）模型得到三个变量的条件方差变量，分别用gp_ch、qh_ch、zj_ch表示。

（三）贝叶斯向量自回归（BVAR）模型估计

1．变量平稳性和VAR系统平稳性检验

为了避免因为单位根现象而出现对模型估计结果不准确，首先进行各变量的平稳性检验。通过ADF检验，发现gp_ch（ADF－1．815）、qh_ch（ADF＝－2．716）分别在10%、1%水平下平稳，而zj_ch（ADF＝－0．706）呈现I（1）特征。我们将zj_ch差分以后用dzj_ch（ADF＝－6．201）表示，和另外的两个变量①按照很多文献的做法，进行VAR建模时一般要求所有变量平稳。此处我们发现gp_ch和qh_ch均是平稳的，只有zj_ch不平稳。原变量是表示波动情况，差分一次后经济意义解释可作相近理解，不影响分析。建模，根据LR、FPE、AIC等信息准则确定最佳滞后阶数为1。经过VAR系统检验发现是平稳的，可以进行后续的BVAR和脉冲响应分析。

2．贝叶斯向量自回归（BVAR）设置说明

首先，对于BVAR模型滞后阶数的设置，采用Matlab2010b提供的LR指标，结果显示最佳滞后为2阶。其次，BVAR模型估计方法需要事先设定超参数以反映模型的先验信息。本文借鉴相关文献，经过多次调试，最终将BVAR模型的超参数设置为：nlag＝2（滞后阶数）；weight＝0．5（权重矩阵）；decay＝1；tight＝0．1（衰减参数，Minnesota先验信息）；odum＝＇o1＇（代表Cholesky分解）。

图1 股票市场的脉冲响应图

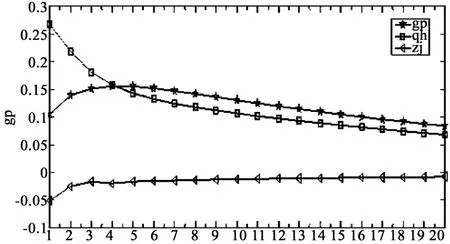
图2 期货市场的脉冲响应图

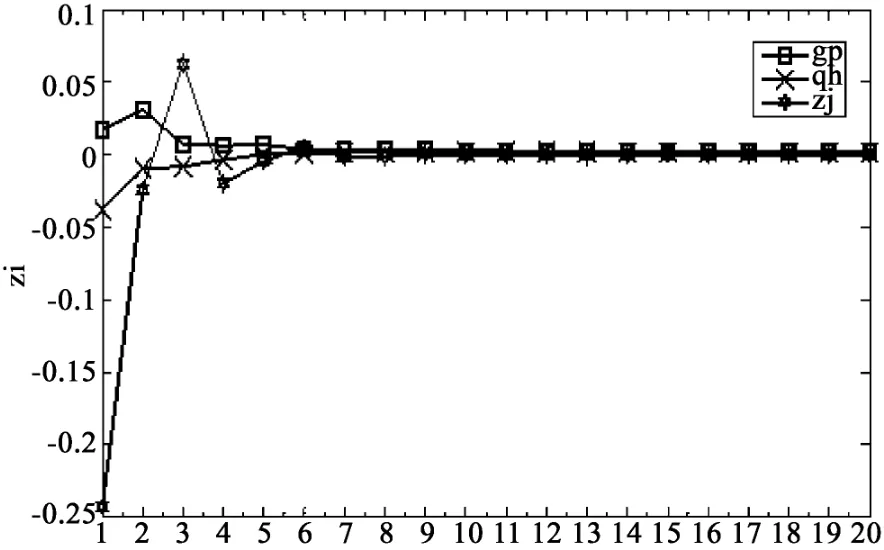
图3 债券市场的脉冲响应图

（四）贝叶斯向量自回归（BVAR）脉冲响应分析

1．股票市场的脉冲响应分析

从图1可以看出，当期货市场当期遭到一个标准差的正向冲击，股票市场第1期会产生正向的冲击响应，强度为－0．005；第2期开始上升，至第6期达到最大强度0．2465；此后逐渐下降。而如果债券市场受到一个标准差的波动冲击后，股票市场的在第1期响应非常微弱，从第2期开始影响增强，但是对股票市场的影响一起呈现负向关系，持续期较长，但影响十分微弱。而股票市场对来自自身市场冲击后的反应是最为强烈的，在第一期就会产生一个强度大小为0． 643的正向响应，第2－5期影响显著下降，至第6期的影响趋于平缓只有0．3374左右，此后逐渐接近削弱，这也正好说明股市风险大的特性。

2．期货市场的脉冲响应分析

从图2可知，给定债券市场波动的一个单位标准差正向冲击，期货市场在第1期产生一个较大的负向响应，强度为－0．051；第3期影响减弱为－0．017，第4期以后逐渐变得平缓，但是整个影响均为负。而针对来自股票市场波动的一个单位标准差正向冲击，期货市场波动冲击第一期响应值为0．105，第4期达到最大值0．158，此后影响逐渐减弱。而期货市场对来自自身冲击的响应情况来看，第1期为响应最大、强度为0．267，第2期显著减少，第6期响应强度减弱为0．132，此后缓缓减弱。

3．债券市场的脉冲响应分析

从图3来看，国债市场对来自自身市场的冲击反应最为剧烈，第1期产生一个强度为－0．243正向冲击；第2期减弱至－0．024；第3期影响为正，且达到最大值0．063，此后影响递减有逐渐消失。股票市场受到一个单位标准差的冲击后，国债市场的响应整个后续时期均不大，第1期产生一个强度为0．017的影响；第2期的影响达到最大0．031；此后慢慢消失。而对来自期货市场一个单位标准差的冲击后，债券市场首期响应为－0．038，此后的影响非常微弱。

四、结论与启示

本文通过建立贝叶斯向量自回归（BVAR）模型，对股票、期货、国债等市场间风险传染进行了研究，得到如下结论：第一，从三大市场增长的情况和波动信息统计指标来看，股票市场在近11年增长速度最快，其市场波动幅度也最大。而国债市场的增长速度最小，波动情况居中。期货市场增长速度居中，波动幅度最小。第二，从因果关系检验结果来看，股票和期货市场等高风险市场之间具有较为显著的影响和传染关系。而由于我国国债市场交易和管理制度都相对严格，所以国债市场的抗干扰能力相对较强。第三，从模拟的脉冲响应分析效果来看：（1）股票市场对来自自身市场冲击的当期响应迅速且较大；期货市场冲击的前期影响较小但后续影响时间较长；债券市场冲击对股票市场的影响为负，幅度不大。（2）期货市场对来自股票市场冲击的影响反映较弱；而对来自自身的影响反映强烈，但是时间都较短，这与股票市场非常类似，这些正好验证了股票、期货市场的高风险、高投机性的市场特征；而债券市场波动对期货市场的影响一样为负。（3）国债市场对来自股票市场、期货市场的冲击的响应整个时期都不大。对来自自身冲击的响应也只显著响应3期后，影响快速减弱。

针对本文实证分析结果，结合我国当前的金融形势，可以得到以下启示：第一，培育良好有序的金融环境，认真监管与规范债券市场的运营操作，重点关注债券市场与股票、期货市场的融合机制。从granger因果关系检验和脉冲响应分析可以看出，由于我国对债券市场管理较为严格，其与别的市场具有相对独立性，股票市场和期货市场上的某种随机冲击均不会轻易引起债券市场大幅振动。但是反过来，由于债券市场长期以来都是一种在被保护的机制下运作，形成了债券（国债占大部分比重）市场相对高安全性。一旦最安全性事物受到某种实质性的外部冲击，带来的影响可能是巨大和负面的。从前述脉冲响应分析来看，债券市场的某种波动冲击对股本、债券均是产生负向的影响路径。所以，有必要重点引导债券市场如何和其他市场协调发展机制的设计，使其经营操作变得更加灵活、弹性更大。第二，股票和期货市场之间的感染能力较强，且granger因关系显著，说明了它们的高投机性与虚拟性，从而导致风险更容易市场中传递。加大对高风险市场的监督管理，尤其针对股票、期货市场。

［1］王宝，肖庆宪．我国金融市场间风险传染特征的实证检验［J］．统计与决策，2008（11）：78－79．

［2］蒋序怀，吴富佳，金桩．当前资本市场的风险传导机制——基于传染效应的实证分析［J］．财经科学，2006（2）：16－24．

［3］陈燕武，黄静菲．利用非参分位数回归模型分析金融市场的风险传染［J］．华侨大学学报（自然科学版），2013（2）：215－219．

［4］陈庭强，何建敏，尹群耀，等．基于银行信贷行为的CRT市场信用风险传染评述［J］．金融理论与实践，2011（11）：95－99．

［5］兰鹏，李铭．波动溢出、风险传染与信息传递效应——基于亚洲股票市场的实证研究［J］．哈尔滨商业大学学报（社会科学版），2012（2）：16－24．

［6］华桂宏，周茂彬，成春林．银行体系、股票市场与固定资产投资——基于三元向量自回归模型的格兰杰因果关系检验［J］．财贸研究，2008（1）：90－94，146．

［7］张慧莲．证券投资基金和保险资金对股票市场影响的实证分析［J］．金融理论与实践，2010（01）：81－85．

［8］THEODOSSIOU P，KAHYA E，KOUTMOSG，etal．Volatility Reversion and Correlation Structure of Returns in Major InternationalStock Markets［J］．Financial Review，1997，32（2）：205－224．

［9］KINGM A，WADHWANIS．Transmission of Volatility between Stock Markets［J］．Review of Financial Studies，1990，3（1）：5－33．

［10］HAHM S．Transmission of Stock Returns and Volatility：the Case of Korea［J］．The Journal of Korean Economy，2003，5（1）：17－45．

［11］PARK Y C，SONG CY．Financial Contagion in the East Asian Crisis：With Special Reference to the Republic of Korea［R］．Korea University Working Paper，2000．

［12］LESAGE JP．Applied Econometrics Using MATLAB［M］．Department of Economics University of Toledo，1999．

［13］LITTERMAN R B．Forecasting with Bayesian Vector Autoregressions－Five Years of Experience［J］．Journal of Business and E-conomic Statistics，1986，4（1）：25－38．

［14］SIMSC A，ZHA T．Bayesian Methods for Dynamic Multivariate Models［R］．Federal Reserve Bank of Atlanta Working Paper，1996：96－13．

［15］ENGLE R F．Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation［J］．Econometrica，1982，50（4）：987－1008．

An Em pirical Study of Volatility Spillover Effects of China Stock，Bond and Futures M arkets——Based on GARCH－BVAR Model

LIXin-guang1，ZUO Shuo-zhi2
（1．School of Business，Wuyi University，Nanping 354300，China；2．School of Statistics and Mathematics，Yunnan University of Finance and Economics，Kunming 650221，China）

Based on the data of stock turnover，futures turnover and bond turnover from December 2002 to February 2013 aswell as themarket volatility information obtained via GARCH（1，1）Model，the infective process of the above-mentioned market volatility is simulated through Bayesian Vector Autoregressive Model（BVAR）and Impulse Response Function（IRF）．The results show that both stock market and futures market respond strongly to their self-impactwhile the impact of futuresmarket on bond market is weak but continues for a long time，with a weaker impact of bondmarketon futuresmarket；and that the impactof bondmarket and futuresmarketon the treasurymarket are quite weak in the whole sample period．

Bayesian Vector Autoregressive Model（BVAR）；GARCH Model；futuresmarket；stock market；bond market

F830．91

A

1008－2670（2014）04－0023－06

（责任编辑 高 琼）

2014－03－28

福建省教育厅项目“区域物流与旅游业协调发展的对策研究——基于福建省数据的实证分析”（JA11273S）。

李新光，男，湖南娄底人，武夷学院商学院讲师，华侨大学经济与金融学院博士生，研究方向：宏观经济模型及应用、金融计量模型分析及应用；左硕之，男，福建建阳人，云南财经大学统计与数学学院。