现代信用风险度量模型的最新理论研究进展

王新军，吴建华，张 颖

(1.山东大学经济学院，济南 250100;2济南大学数学科学院，济南 250022)

一、引 言

20世纪90年代以来，金融风险越演越烈，金融危机和银行危机在世界范围内频繁爆发，使全球金融体系特别是银行业经历着持续不断和持续增长的信用损失，每次金融危机都会给某些国家、地区乃至全球经济带来巨大的冲击。尤其是2008年爆发的美国次贷危机，不但重创了美国金融体系，使得以金融创新著称的华尔街颜面尽失，更是波及全球金融体系和实体经济。值得一提的是，美国次贷危机实际上是一场典型的信用危机，它再次引起全球对信用风险管理的高度重视。对于2008年的次贷危机，许多人将其归咎于信用市场的过度发展，更是将结构化信用衍生品指为罪魁祸首。然而，任何一种金融产品，只是某种交易工具，它作为市场的交易客体，其内在属性是被动的，本身不具有主观性，它所表现出来的善良与邪恶，实质上反映了背后从事交易的各类市场主体的行为。实际上，2008年的信用危机的根源主要有三，第一，金融机构内部激励约束机制不对称和虚假的财务报告是危机发生的内部原因;第二，信用评级机构的虚假评级和金融监管的人为缺失是外部原因。第三，从金融产品设计的微观层面来分析，忽视“不完全信息”，导致违约风险、违约传染和信用衍生产品定价被低估，是信用危机产生的技术性原因。

从国内来看，目前，中国金融市场的改革已进入深水区，表现在利率决定机制进一步市场化，金融机构进入门槛降低和民间金融逐步合法化等。一方面市场化会提高金融运行的效率，增强价格的信息传递作用，同时由于自由市场系统本身的复杂性，市场化必然会增加整个金融体系的不确定性因素，导致系统性信用风险的增加。同时，目前的中国经济社会还存在着几个重大的金融问题，比如旧有的中小企业的融资困境，正在进行的新型城镇化建设需要巨量资金支持，银行体系内日益累积的巨大的房地产信贷违约风险。这些都需要进一步发展债券市场和信用衍生品市场。但是，中国目前的信用产品市场发展严重滞后，不但债券市场交易不活跃，而且缺乏有效的信用衍生品市场，流动性严重不足。信用衍生品可以为银行、企业和投资者提供以较低成本管理信用风险的有效工具。虽然在2000年，资产支持证券化(ABS)在中国就正式出现，但是发展缓慢。在经过了长达10年之后，信用风险缓释工具(CRM)交易(中国版的CDS)才于2010年10月正式引入，但是由于现行的金融体制和金融市场发展落后的制约，信用衍生品的二级市场几乎没有发展。此外，中国的信用评级市场发展落后，信用市场数据严重缺失，信息不对称情况非常严重，在这种情况下，无法将国外现有的信用风险模型直接用于中国市场上信用风险的度量及对冲和衍生品定价。因此，无论是当前中国亟需解决的融资需求问题，还是房地产信贷集中违约风险，都需要对信用风险度量、对冲策略和风险定价机制进行深入的理论研究。

然而从国内目前的研究现状来看，关于信用风险度量的研究，更多的是对现有国外应用模型的综述、对比和利用中国数据进行的实证分析，比如KMV模型、CreditMetrics模型，CreditRisk+模型和Credit Portfolio View模型等。相比而言，理论模型的研究相对较少。鉴于此，本文希望通过回顾国外信用风险模型的理论研究，详细分析信用风险度量模型理论研究的路径，为深入开展信用风险度量模型的理论研究奠定基础。

我们将按照现代信用风险度量理论模型出现的时间先后和建模机制的不同，从三个方面来综述现有的文献:基于BS定价理论的内生违约机制研究、基于随机点过程的外生违约机制研究和基于非线性滤波的条件违约机制研究，最后预测目前信用风险度量理论模型的最新研究进展。

二、基于BS定价理论的内生违约机制——结构信用风险模型

(一)Merton模型

现代信用风险度量模型最早起源于Merton［1］，他将Black-Scholes的期权定价理论引入信用风险度量中，将企业的股权看成是以资产为标的、以债务面值为执行价格的看涨期权。在债务到期日，当企业的资产价值小于负债时，企业将放弃股权，出现债务违约。然后，利用B－S期权定价公式，对股票和债券进行定价，进一步推导出债务违约概率。Merton模型是结构信用风险模型的基础模型，用公式表示为:

式(1)中α为瞬时预收益率，Ct为收益支付，σt为瞬时波动率，Bt为标准布朗运动。

Merton模型除了假设市场是无套利和完备的以及不考虑税收等因素之外，还有以下几个关键的假设:

A1:企业的资本结构非常简单，只有股权和零息债券。

A2:违约只能在债券到期日发生，且违约门限D是固定的，由债务外生确定。

A3:无风险利率r具有常数水平的期限结构。

A4:资产价值V服从连续扩散的随机过程。

Merton模型之后所发展出来的结构模型，都是通过放宽这几个假设实现的。

(二)结构模型的发展

1.首达时模型

Black和Cox［2］放松了Merton模型的假设A2中关于违约只发生在债务到期日的设定，将违约时间τ定义为企业资产价值V 首次低于某个门限D 的时刻，在债务到期日之前，只要企业资产价值低于特定门限值，违约就会发生，从而建立了首达时模型。首达时模型的设定更加符合真实的违约实际，因此，后面的许多模型都是以此为基础进一步发展的。此外，首达时模型中还引进了“即时清算”的安全条款假设:在到期日前任何时刻，如果企业发生违约，债权人可以对企业立即实施强制破产，并获得企业的全部资产。对于“即时清算”这个假设，Francois和Morellec［3］认为按照现实的破产法律程序，违约只表示一个清算过程的开始，而不会立即导致企业清算。当债务到期后，或者导致清算，或者并不导致清算。他们提出了“延迟清算”的假设:只有当资产价值低于门限值并且超过既定的时限时，企业才会被清算。但是于清算过程的不确定性，使得该模型难以进行实证检验，在实践中也难以获得应用。

2.随机违约门限结构模型

在Merton模型中，假设A2还设定违约门限D是固定的，由债务外生确定。Longstaff和Schwartz［4］在首达时模型框架内，将外生的违约门限推广到了时间t的确定性函数D(t)的情况。而Briys和Varenne［5］，Hsu等人［6］将外生的违约门限值或者Vt/D比率放松为随机过程，并且获得违约概率的数值解。Leland［7］则认为企业的内部人员(经理人或股东)可以自行决定违约门限水平，因而违约门限值是内生的、主观随机的。

3.随机利率结构模型

在Merton模型中，A3假设无风险利率r为常数，但在现实市场中，无风险利率通常会随着时间改变，而且与资产价值往往存在一定的相关性。为此，许多学者将随机利率期限结构引入到信用风险模型中。比如，Kim等人［8］，他们假定利率rt服从风险中性的CIR过程，见式(2):

式(2)中a是均值回复因子，b是rt的长期均值，σr是利率波动率，Wt服从标准布朗运动。虽然该模型不能得到封闭解，但是可以生成更为现实的违约互换溢价。

Shimko和Tejlma［9］假设短期利率服从更一般的Vasicek过程，见式(3):

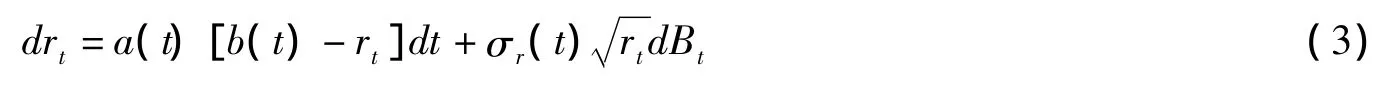
式(3)中rt是利率，a(t)是均值回复因子，b(t)是rt的长期均值，σr(t)是利率波动率，且a(t)，b(t)，σr(t)是一个关于时间的确定性函数。Bt服从标准布朗运动。

随机利率的引进使得模型更符合实际。它考虑了利率过程和资产价值过程之间的相关性，而且修正了标准结构模型中过于简单的破产规则。然而，随机利率的引入使得结构模型分析变得较为复杂，很难获得封闭形式的表达式，只能使用数值方法。

4.复杂资本—债务结构模型

在Merton模型中，A1假设企业的资本结构非常简单，只有股权和零息债券。但现实中，企业的资本结构往往非常复杂，债券不仅带有票息，本身也可能具有优先偿付的安排等。因此，一些研究者提出了更具现实性的资本债务结构，Geske［10］把企业的债务看成是一个付息债券，利息的每一次支付被看作一个复合期权并可能引起违约。Vasicek［11］考虑了存在短期债和长期债的情况的债务结构;Ho和Singer［12］考虑了含有优先规则、支付计划、沉淀资金等等债务条款的情形。

5.基于跳扩散过程的结构模型

需要注意的是，无论从违约门限、利率结构和资本债务结构任何一方面的拓展，只要企业的资产价值过程是扩散过程(假设A4)，结构模型都存在一个自身无法克服的缺陷:违约时间是一个可料的停时。即在完全信息下，投资者可以提前知道可能的违约时间，这意味着，无论企业面对的风险大小如何，随着到期日的临近，企业的收益价差趋于零。零值的短期信用价差表明，在短期内没有违约风险。这同真实的市场中非零的短期信用价差是不符的。事实上，在真实的二级市场上，由于投资者不确定当前的资产在下一个时刻是否会趋近于违约临界水平，因此，投资者因为承担了这种不确定性所带来的违约风险，所以，他们需要对此索取非零的风险溢价，这就导致我们在实际市场上看到的短期信用价差非零的现象。

针对企业的价值是连续扩散过程的假设。Zhou［13］假设企业的资产价值V服从某个跳扩散过程，见式(4):

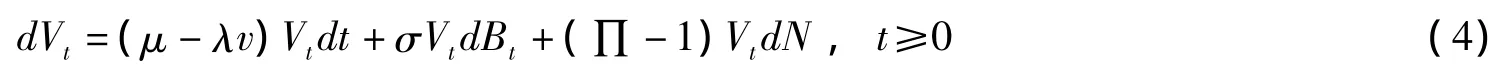
式(4)中μ表示企业资产的预期收益率，v，λ，σ为正的常数，B为标准布朗运动，∏＞0为跳跃度，均值为v+1，且服从某个对数正态分布，dN为具有强度λ的齐次Poisson过程，并且dB，dN和∏互相独立。在某些假设下，推出了债券的定价公式，并且获得了非零的短期信用价差。之后，Hilberink和Rogers［14］考虑了允许企业价值从上向下跳跃的Levy过程。Seherer［15］考虑了资产价值可以从上向下和从下向上两个方向的跳跃，假设资产价值服从一个双指数跳跃过程。并推出了债务、企业价值和最优障碍水平的封闭形式解。相对于纯跳跃模型，这种具有非零限制的价差期限结构也更符合实际。

(三)对结构模型的简评。

结构模型揭示了企业违约发生背后的经济学机制，说明了公司资产结构变化对公司违约的影响。但是，结构模型不能解释现实的市场中存在的非零短期信用价差的现象。虽然跳跃成分的引入在一定程度上解决了结构模型隐含的违约时间可料的缺陷，可以从理论上对实际观测到的违约概率、回收率以及信用价差做出一定的解释。但缺陷在于当用模型校验市场数据时过于复杂，跳跃并不一定暗含着违约。此外，跳扩散结构模型无法区分新增市场信息和稀有事件(如巨灾、技术革新、竞争者的进入、政治风险等)对企业的资产价值造成的不同冲击，因而也就无法得到信用衍生品的定价公式。

随着结构模型的发展，另一个信用风险建模的方法——基于强度的方法，或者称为简约模型迅速发展了起来，简约模型不但能够避免结构模型可料的违约停时的缺点，而且因为它在计算上的易操作性，从而在风险定价中被广泛采用。下面详细介绍简约模型。

三、基于随机点过程的外生违约机制——简约信用风险模型

同结构模型的建模方式不同，简约模型放弃了根据企业的资产和负债来模型化违约风险，而是将违约直接看做由外生的随机点过程决定的不可预期的随机事件，将违约时间定义为某个计数点过程的首次跳跃时间，这样做的好处是，违约时间变成了一个完全不可料的停时，从而避免了结构模型对短期信用价差低估的缺点。由于简约型模型的核心假定是:对该计数点过程的强度的设定，因此也称之为强度模型。下面以简约模型构建时间先后和关键设定的不同，综述简约化模型的研究脉络

(一)简约模型的提出与发展

1.JT模型——常数违约强度

Jarrow和Turnbull［16］首次提出了信用风险度量的强度模型。该模型假设市场是无套利且完备的，假设违约强度λ为常数，违约时间τ定义为具有参数λ的Poisson过程的第一次跳跃，τ服从具有参数λ的指数分布。证明了在无风险利率计价单位下，能够得到唯一的风险中性测度——鞅测度。利用该模型可以将有违约风险的金融工具(比如，含息企业债券、企业债券的远期和期权、美式期权以及脆弱期权)的价值表示成风险中性测度下的贴现值。从而可以推导出可违约债券价格的D(t，T)计算公式。如果已知债券的价格和违约回收率，还可以使用递归方法反求出风险中性概率q0，q1的值。

该模型有两个关键假设。第一，回收率是外生常数。此假设意味着回收率独立于任何状态变量，并可估计。第二，不管是在实际概率下还是在风险中性概率下，违约强度都是外生常数。这一假设的结果是，在债券的整个生命期内，违约概率总是相等的。

但该模型的缺点在于:违约发生后，债券的信用等级不变，且违约之后债券就没有违约风险了，显然与真实的市场表现不符。于是，Jarrow、Lando和Turnbull对该模型进行了扩展。

2.JTL模型——时变的确定性违约强度

为了克服常数违约强度模型的缺点，Jarrow、Lando和Turnbull［17］不再将违约视作一个突发事件，而是从一个较高的信用等级向违约转变的过程，把违约过程与信用评级联系起来。用一个时齐的有限状态马尔科夫链状态空间表示信用评级，马尔科夫链的转移概率矩阵即为信用评级转移矩阵，吸收状态代表违约。违约强度不再是常数，而是随着时间而变，即转移概率。违约时间τ定义为首次达到吸收状态的时间。马尔科夫链的状态变量用信用等级{1，2，...，K}表示，K－1代表最低的信用等级，K代表违约，是一个吸收态。

在离散情况下，信用评级转移矩阵可表示为:

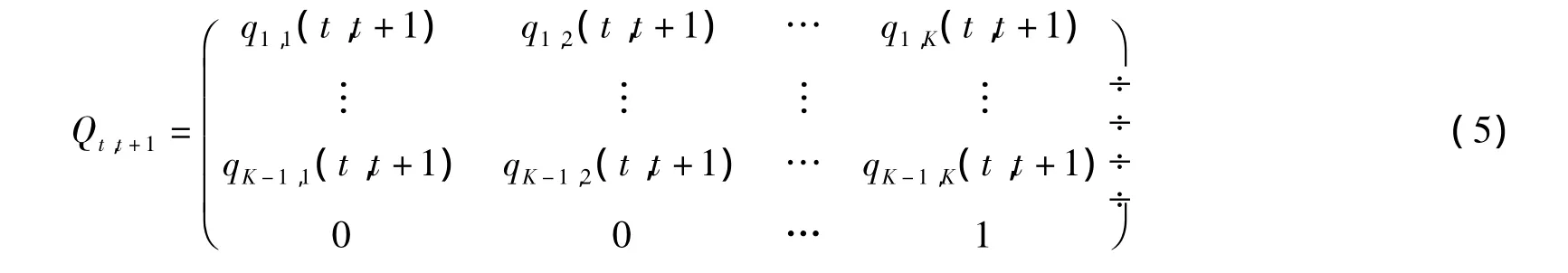
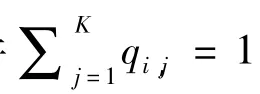
在连续情况下，当λ=λ(t)为时间t的确定函数时，违约时间τ就是具有强度λ(t)的非时齐Poisson过程的首跳时间。此时就可以求出相关的违约概率和可违约证券的价格。如果已知无风险利率和回收率，利用可违约证券信用价差的市场数据就也可以估计出风险中性测度下的危险率函数λ(t)。

JTL模型的优点在于它可用于参数评估，还可以用于更复杂的债券和违约互换等衍生工具的定价。但是，JTL模型保留了利率与违约强度相互独立的假定。这样即使利率为一个随机过程，债券的信用价差与利率变动也不相关，这显然与现实不符。另外，在JTL中，信用评级变化会导致信用价差变化。然而现实的情况是，信用评级的变化往往落后与市场信用价差的变化，而且甚至即使评级不变，债券的价差也有可能变化。为此，Das和Tufano［18］假定违约回收率也具有随机性，且与无风险利率相关。这样信用价差不再单纯是信用等级的函数，即使某一企业债券的信用等级不变，信用价差也可能发生变动。通过假定违约回收率的随机性，该模型还可以用于对更广泛范围内的各种债券和衍生工具进行定价。

3.Lando模型——随机违约强度

对JTL模型的实质性的拓展工作是由Lando［19］完成的，他研究了不同信用级别的期限结构，并允许信用价差即使在信用级别不变的情况下也能随机运动，提出了Cox信用模型。

Lando进一步放松了违约强度，假设违约强度为随机过程，即λ={λ(Xt)t≥0，λ:Rn→［0，∞)是一个连续非负函数。给定概率空间(Ω，Gt，P)，0 ≤ t≤ T，其中，Gt=Ft∨ Ht，Ft= σ{Xs:0 ≤ s≤ t)，表示时刻 t之前的所有可能的状态变量，Ht=σ{1{τ≤s}:0≤s≤t}，包含了在时间t以前是否有违约发生的信息。状态变量X={Xt:0≤t≤T}是左极右连的随机过程，它可以包括与违约相关的变量(比如，无风险债券的利率，股票价格，信用价差等)，并且和指数随机变量E相互独立。随机违约强度λ(Xt)的直观意义就是，在一家企业已经生存到时间t的条件下，在下一个瞬间Δt内违约的概率为λ(Xt)·Δt+o(Δt)。

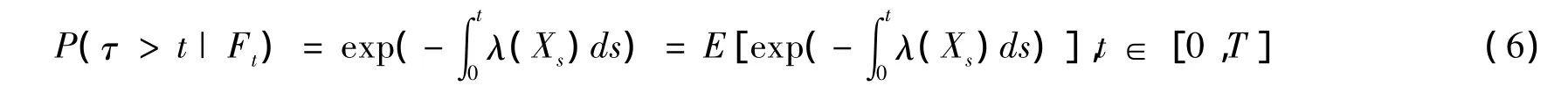
如果已经知道或有支付和回收率，可以对可违约证券定价。这一方法扩展了JTL模型，通过用相同的状态变量来决定利率和违约强度，该模型允许违约强度和利率运动相关联。

4.信用风险期限结构模型

对于简约模型来说，它的主要优势在于，给风险资产定价。受到无风险利率期限结构模型的启发，Duffie和Singleton［20］提出了另一类简约模型——信用风险的期限结构模型。他认为信用风险债券可以像无风险债券那样，直接利用风险债券利率进行贴现求取现值。风险债券的利率等于无风险利率加上一个信用风险调整系数。这样，只需要将无风险利率期限结构模型中的无风险利率替换为风险债券的贴现率，就可以从无风险利率期限结构模型中导出风险中性概率下信用风险债券的价格。于是，所有的利率模型都可以直接用来定价信用风险债券。

Duffie和Singleton考虑了违约相关性和利率风险，将违约事件定义为是由死亡率过程决定的不可预测事件。假设违约时间服从强度为λt的Poisson过程。那么，在风险中性测度下可以得到如式(7)的债券风险溢价:

由式(7)可知，模型中风险贴现利率包含了三个组成部分，分别是无风险利率、违约强度以及违约回收率，这三个都可以被视作随机变量，并且彼此之间皆可具有相关性。

Duffie和Singleton模型为应用无风险利率期限结构的思想来给信用风险债券定价提供了一个良好的框架，丰富了关于期限结构的理论，从而可以利用市场观测的数据进行违约过程的参数估计。模型还将市场风险因素引入到信用风险定价中来，得出即使信用等级不发生变化信用利差也可能改变的结论，这也克服了同一等级的信用风险价格相同的问题。但是由于违约强度是外生给定的，因此掩盖了违约背后的经济机制，这是该类模型的主要缺陷。在此基础上，Duffie、Pan 和 Singleton［21］及 Duffie、Filipovic 和 Schachermayer［22］建立了跳扩散仿射强度模型。

(二)对简约模型的简要评述

简约模型对外生性违约强度的假设，使得违约时间成为了一个完全不可料停时，推导出了同实际市场一致的非零短期信用价差，而且从计算和实际应用来看有很强的可操作性，因而在金融行业中被广泛应用于信用风险产品的定价中。但是，简约模型没有清楚的解释违约发生的经济学原因，因此通常这些模型不能用于预测企业的违约风险。

四、基于非线性信息滤波的条件违约机制

前面所提到的结构模型和简约模型都是在完全市场的前提假设下建立的，完全市场的假设意味着，企业内部人员和外部的市场参与者对企业的财务状况和经营管理具有完全相同的信息。虽然结构模型和简约模型采用了两种不同的建模范式，但实际上两类模型之间存在着内在的联系。从模型的信息结构来看，结构化模型是以完全信息为基本假设的。它假定企业的财务报告是真实的、准确的，而且企业内部人与市场参与者所掌握的信息是完全对称的，特别是市场投资者可以连续观测到企业的资产价值V和债务D。而简约化模型假设市场投资者只能观察到历史违约时间τ和决定违约强度λ的状态变量X的信息，显然这种信息量要小于结构模型下的完全信息量。因此，结构模型可以看成是具有完全信息的简约模型，两类模型的不同仅仅在于信息的设定不同。

实际上，在真实的金融市场上，企业的内部人与外部的市场参与者之间的信息是不对称的，企业外部的市场参与者，尤其是二级市场上的债务投资者只能获得企业的财务和经营管理的不完全信息，即带有噪音的、被人为扭曲的信息或者是不完整的部分信息。不完全信息的存在会导致市场参与者做出错误的判断，特别是会低估企业的违约风险和违约相关性，从而得出错误的信用风险定价。这使得市场参与者无法正确的预测信用产品市场上信用价差的异常波动和企业资产的信用质量的变化，最终导致债务投资者在企业的实际违约甚至破产中遭受巨大的损失。

因此，将不完全信息纳入到信用风险度量中，不仅能够在理论上将结构模型和简约模型统一到一起，更重要的是，在模型应用中，可以使得信用风险的度量和定价更加符合真实的信用产品市场。下面根据不完全信息引入的模型不同，综述现有的不完全信息下信用风险模型的研究路径。

(一)将不完全信息引入现有的结构模型

Duffie和Lando［23］注意到了结构模型和简约模型之间的关键差别在于信息的设定不同，提出了一个新的模型，假设具有内生的违约门限，但是企业的财务报告是含有噪声和滞后的，市场参与者必须从中推断出企业的真实的资产，因此市场参与者拥有的是不完全信息。该模型推出了非零的短期信用价差，从而将结构模型和简约模型的统一到了一个框架内。

沿着Duffie和Lando的思路，Giesecke和Goldberg［24］在首达时模型的框架内，假设企业的资产价值过程V是可以被完全观察的，但是违约门限是随机的且不可观测的。这种随机性门限的设定使得违约时间τ就是完全不可料的。最后得到了一个结构—简约混合违约模型，记为I2，这种模型同时具有结构模型的经济意义和简约模型的容易计算的定价公式和对市场数据的校准的优点。Giesecke和Goldberg［25］在违约门限不可观测的条件下，将I2模型进行了拓展，说明了信息不对称会对信用风险溢价的结构具有重要影响。该拓展考虑了违约发生时证券价值的突然下跌的现象

Cetin等人［26］提出市场投资者信息集合是经理人的信息集合的严格的缩减子集。而且将资产价值定义为是企业的现金流，相应的违约门限则变成了Lt=0，t≥0。将违约时间定义为现金流首次小于零的时刻。部分信息子集的设定使得违约时间是完全不可料的，最后得到了一个基于强度的危险率模型。

Guo等人［27］提出了利用“滞后滤波”的概念来刻画不完全信息的思路。通过一个简单的例子，说明了滞后信息的重要性。最后，在不同的信息滤波下初步研究了风险债券定价之间的关系。

Frey和Schmidt［28］利用随机滤波技术，处理了不同设定下的不完全信息问题，在部分信息条件下考虑了企业证券(股票和债券)的定价问题。Cetin［29］在不完全信息框架内，考虑了一般化的马尔科夫设定下，违约的指示函数具有一个绝对连续的补偿子，讨论了由一族半鞅方法向滤波的投射，在这种设定下，推出了违约资产的定价公式。Frey和Lu［30］假设企业资产价值为不完全信息条件下，说明了典型的企业证券(比如，股票，企业债券或CDS)的定价问题会导致非线性滤波问题。利用Dellacherie公式，将该问题转换成关于一个停时的扩散过程的标准的滤波问题。利用滤波中的SPDE分析了该问题。给企业的证券价格的机制给出了一个明确的描述，简要解释了如何利用该模型来给债券和股票期权定价。

从上面的现有文献可知，在不完全信息下的结构模型的研究中，更多的是采用非线性滤波技术来处理模型参数的估计和预测问题。

(二)将不完全信息引入现有的简约模型

基于不完全信息的简约模型的研究相对较少。Collin等人［31］假设违约强度由一个不可观测的因子过程所决定，市场参与者所拥有的信息由某些经济变量和债务的违约历史决定。违约时间假设为服从信息条件下独立的双随机变量过程。Frey和Schmidt［32］将不完全信息引入简约模型下的定价模型，其中违约强度由某些因子决定，这些因子不能被市场参与者直接观察到。市场参与者所拥有的信息集合由违约历史和可交易信用证券价格的噪声观察值构成。

另外，Hainaut和Robert［33］还首次提出了部分信息下的信用评级转移模型，给出了三种不同的部分信息:具有预设的滞后期到达的评级信息，根据外生的Poisson过程随机到达的信息和根据内生的规则到达的信息。在这三种部分信息下，推导出了债券和期权的价格，并且提供了在真实的测度和定价测度下债券价格的生成机制。

(三)对现有的不完全信息信用风险模型的评述

以上这些文献只是不完全信息信用风险度量的一些零散的研究，目前还没形成完整的不完全信息信用风险度量体系，需要对以下几个问题进行系统的思考和研究:①信息集合的具体结构和不完全信息的数学描述;②不完全信息对违约概率的影响以及影响程度;③在组合类信用风险度量中，如何在不完全信息下对违约相关性进行度量;④在信用衍生品定价中，不完全信息如何进入定价公式中，如何求解不完全信息下的衍生品定价公式，是利用解析方法还是数值计算方法。

五、结 语

本文梳理了现代信用风险度量的理论模型的研究路径，从目前的研究现状来看，对于信用风险度量模型的理论研究，已经从完全市场假设条件，转入不完全市场条件，尤其是不完全信息条件;即在不完全信息下如何刻画违约概率、违约相关性和信用衍生品定价等问题。对于不完全信息的引入，研究中所使用的工具，更多的是非线性信息滤波技术。将不完全信息引入到现有的信用风险度量模型中，不仅能将结构模型和简约模型统一到一起，而且可以使信用风险的度量更符合真实的金融世界。

［1］MERTON R C.On The Pricing of Corporate Debt:The Risk Structure of Interest Rates［J］.The Journal of Finance，1974，29(2):449－470.

［2］BLACK F，COX J C.Valuing Corporate Securities:Some Effects of Bond Indenture Provisions［J］.The Journal of Finance，1976，31(2):351－367.

［3］FRANCOIS P，MORELLEC E.Capital Structure and Asset Prices:Some Effects of Bankruptcy Procedures［J］.The Journal of Business，2004，77(2):387 －411.

［4］LONGSTAFF F A，SCHWARTZ E S.A Simple Approach to Valuing Risky Fixed and Floating Rate Debt［J］.The Journal of Finance，1995，50(3):789－819.

［5］BRIYS E，DE VARENNE F.Valuing Risky Fixed Rate Debt:An Extension［J］.Journal of Financial and Quantitative Analysis，1997，32(02):239－248.

［6］HSU J C，SAA －REQUEJO J，SANTA-CLARA P.Bond Pricing with Default Risk［R］.UCLA Working Paper，2003.

［7］LELAND H E.Corporate Debt Value，Bond Covenants，and Optimal Capital Structure［J］.The Journal of Finance，1994，49(4):1213－1252.

［8］KIM I J，RAMASWAMY K，SUNDARESAN S.Does Default Risk In Coupons Affect The Valuation of Corporate Bonds:A Contingent Claims Model［J］.Financial Management，1993:117 － 131.

［9］SHIMKO D C，TEJIMA N，VAN DEVENTER D R.The Pricing of Risky Debt When Interest Rates Are Stochastic［J］.The Journal of Fixed Income，1993，3(2):58－65.

［10］GESKE R.The Valuation of Corporate Liabilities As Compound Options［J］.Journal of Financial and Quantitative Analysis，1977，12(04):541－552.

［11］VASICEK O A.A Series Expansion for The Bivariate Normal Integral［J］.Journal of Computational Finance，1998，1(4):5 －10.

［12］HO T，SINGER R F.The Value of Corporate Debt With A Sinking－Fund Provision［J］.Journal of Business，1984:315 －336.

［13］ZHOU C.The Term Structure of Credit Spreads With Jump Risk［J］.Journal of Banking ＆ Finance，2001，25(11):2015 －2040.

［14］HILBERINK B，ROGERS L C G.Optimal Capital Structure and Endogenous Default［J］.Finance and Stochastics，2002，6(2):237－263.

［15］SCHERER M.Efficient Pricing Routines of Credit Default Swaps in A Structural Default Model With Jumps［R］.Working Paper，2005.

［16］JARROW R A，TURNBULL S M.Pricing Derivatives On Financial Securities Subject to Credit Risk［J］.The Journal of Finance，1995，50(1):53－85.

［17］JARROW R A，LANDO D，Turnbull S M.A Markov Model for The Term Structure of Credit Risk Spreads［J］.Review of Financial Studies，1997，10(2):481 －523.

［18］DAS S R，TUFANO P.Pricing Credit Sensitive Debt When Interest Rates，Credit Ratings and Credit Spreads Are Stochastic［J］.The Journal of Finance Engineering，1995，5(2):161 －198.

［19］LANDO D.On Cox Processes and Credit Risky Securities［J］.Review of Derivatives Research，1998，2(2 －3):99－120.

［20］DUFFIE D，SINGLETON K J.Modeling Term Structures of Defaultable Bonds［J］.Review of Financial Studies，1999，12(4):687－720.

［21］DUFFIE D，PAN J，SINGLETON K.Transform Analysis and Asset Pricing for Affine Jump—Diffusions［J］.Econometrica，2000，68(6):1343－1376.

［22］DUFFIE D，FILIPOVI?D，SCHACHERMAYER W.Affine Processes and Applications In Finance［J］.The Annals of Applied Probability，2003，13(3):984－1053.

［23］DUFFIE D，LANDO D.Term Structures of Credit Spreads With Incomplete Accounting Information［J］.Econometrica，2001，69(3):633－664.

［24］GIESECKE K，GOLDBERG L R.Sequential Defaults and Incomplete Information［J］.Journal of Risk，2004，7:1 －26.

［25］GIESECKE K，GOLDBERG L R.The Market Price of Credit Risk:The Impact of Asymmetric Information［R］.Working Paper，2008.

［26］CETIN U，JARROW R，PROTTER P，et al.Modeling Credit Risk With Partial Information［J］.Annals of Applied Probability，2004:1167－1178.

［27］GUO X，JARROW R A，ZENG Y.Credit Risk Models With Incomplete Information［J］.Mathematics of Operations Research，2009，34(2):320－332.

［28］FREY R，SCHMIDT T.Pricing Corporate Securities Under Noisy Asset Information［J］.Mathematical Finance，2009，19(3):403－421.

［29］ETIN U.On Absolutely Continuous Compensators and Nonlinear Filtering Equations In Default Risk Models［J］.Stochastic Processes and Their Applications，2012，122(11):3619－3647.

［30］FREY R，LU D.Dynamics of Corporate Security Prices in Firm Value Models With Incomplete Information［R］.Working Paper，2012.

［31］COLLIN-DUFRESNE P，GOLDSTEIN R S，HELWEGE J.Is Credit Event Risk Priced?Modeling Contagion Via The Updating of Beliefs［R］.National Bureau of Economic Research，2010.

［32］FREY R，SCHMIDT T.Pricing and Hedging of Credit Derivatives Via The Innovations Approach to Nonlinear Filtering［J］.Finance and Stochastics，2012，16(1):105 －133.

［33］HAINAUT D，ROBERT C.Credit Risk Valuation With Rating Transitions and Partial Information［R］.Working Paper，2012.