财政调控与国民收入预期

孙中才

(三亚学院 财经学院，海南三亚 572022)

一、引 言

为充分就业而实施的财政政策，最终必将作用于国民收入(GDP)，而且，它的最终效果应该能以国民收入的相应变化反映出来［1］。美国经济学家C.布朗(C.Brown)在1956年就提出了有关的概念——充分就业的预算盈余(Full—Employment Budget Surplus)，该指标可以真实地衡量或测度满足充分就业时的政府预算的盈余状况。也就是要用这个概念来测度充分就业的政府预算在预想的国民收入水平上，或者说在潜在的国民收入水平上所产生的盈余。若这个盈余为正值，那么，就是充分就业的预算盈余;如果这个盈余为负值，那么，就是充分就业的预算赤字［2］。这个盈余不同于实际的预算盈余，其测度应该是潜在的国民收入水平与实际的国民收入水平之间的差值。

布朗的充分就业盈余，可以用公式表示如下:

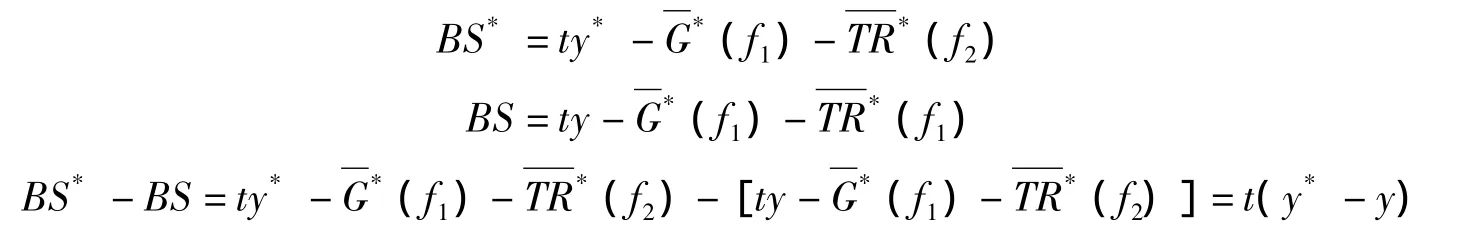
这里，BS*是指潜在的政府净收入;t是指固定税率;y*是指潜在的国民收入;G*(.)是指政府购买;(.)是指政府转移支付;f1是指充分就业决策变量1，针对政府购买的;f2是指充分就业决策变量2，针对转移支付的;BS是指实际的政府净收入;y是指实际的国民收入。

显然，(BS*－BS)的值存在三种情况:(1)BS*－BS＞0，即潜在的政府净收入大于实际的政府净收入，意味着充分就业的政府财政预算G*(.)和TR*(.)是盈余的。若其余不变，这也就是，潜在的国民收入是大于实际国民收入的，即y*＞y。那么，从实际的国民收入y的角度来看，这些预算的实际结果，对于预期的国民收入而言，是紧缩的，因而，就此可以把政府的财政预算视为是紧缩性的;(2)BS*－BS=0，即潜在的政府净收入等于实际的政府净收入，意味着充分就业的政府财政预算正好达到了潜在结果与实际结果的平衡。这样，相应的财政政策是不紧不缩的平衡着的;(3)BS*－BS＜0，正好与(1)相反，意味着，潜在的国民收入小于实际国民收入，即y*＜y。从实际的国民收入y的角度来看，实际国民收入呈现为对预期国民收入的扩张，因而相应的财政政策可视为是扩张性的。

能够看出，布朗所阐述的这个概念是很清楚的，其之所以清楚，是因为人们默认了这里的y*是真实存在的。然而，因为这里的潜在国民收入y*，在以往的经济学范式里难以得到精确地预测和计算，因而，尽管这一概念得到了比较广泛的认可，但关于它的科学解释和精确的表示，却一直没有实现［3］。

随着经济学的科学进展，发现了经济的正则性(economic regularity)和固定替代弹性定律(the law of constant substitution elasticity)等，这些发现为对y*进行解释和测度，提供了更贴切的理论依据［4］。特别是，借助最新的经济学理论范式——有约束的利润函数(restricted profit function)，即G函数，可以更容易地实现有关的初始描述，继之，可以顺利地运用有关引理和定理进行深入的分析，并得出精确的结果［5］。

二、因子间的固定替代与经济的正则运行

设显示财政约束条件的一般经济体，在G函数的框架下可以写为:

式(1)中，π(.)是利润函数;p 是产出价格向量，p=［p1，p2，...，pI］pi＞＞0，i=1，2，...，I;v是需求约束数量向量，v=［v1，v2，...，vJ］，vj≤0，j=1，2，...，J，I＜ J，其中，v1是政府购买，v1=v1(f1);v2是转移支付，v2=v2(f2)。如上所述，这里的f1和f2分别为充分就业的决策变量，其中，f1是针对政府购买v1的;f2是针对转移支付的。

式(1)的Jacobi向量为:

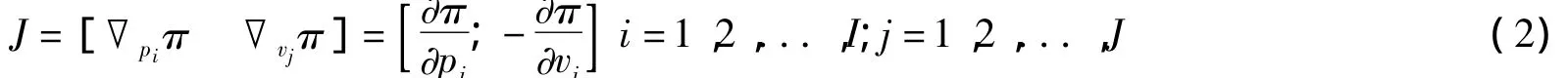
式(2)中，∇是Hamilton算子，即利润关于各个因子的一阶微分。

由式(2)，可以得出式(1)的Hessian矩阵为:

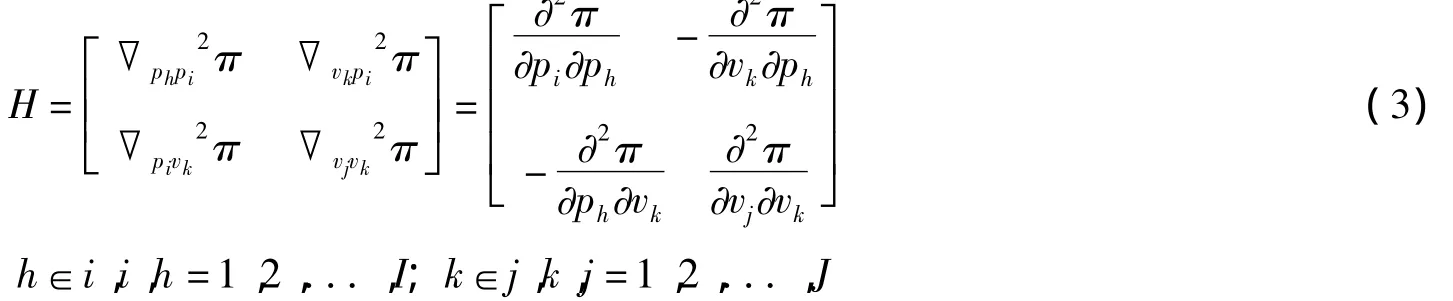
式(3)中，∇2是指Laplace算子，即利润关于各个因子的二阶微分。

式(3)中的各个元素体现了该经济体在运行过程中，各个因子之间在二阶微分水平上的相互作用。

由式(3)可以得出的替代弹性矩阵为:

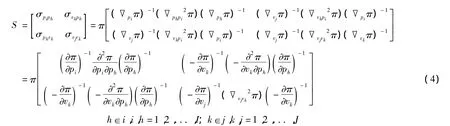
固定替代弹性定律证明，在经济运行中，也就是在经济的增长中，这些替代弹性是固定不变的。经济就是以它们为尺度，遵循正则性和约束条件的最小缩减率规律运行的。约束最小缩减率决定着经济运行过程中实际起着内在作用的那些约束条件的最优增长率，从而保证经济以正则状态来运行。反过来，从经济运行的角度来看，经济的正则运行，必定是遵循这种“最小率”法则的，从而在运行中维护并产生出新的“最小率”，构成最小扩充的经济容量［7］。

通俗地说，约束最小缩减法则就是，在没有其它外来干预的情况下，经济自身的约束条件会客观地依据固定替代弹性所给定的比率，自动地确定自己最小的被替代水平，从而以最放松的水平，保证经济的正则运行［8］。

从数值上来看，约束条件的最小被替代水平，就是最小的真替代减去最大的假替代所得到的差。

对于式(1)，可以在给定的时间基准点(t=0)上，计算出约束条件v1(也就是政府购买)的最小被替代率为:

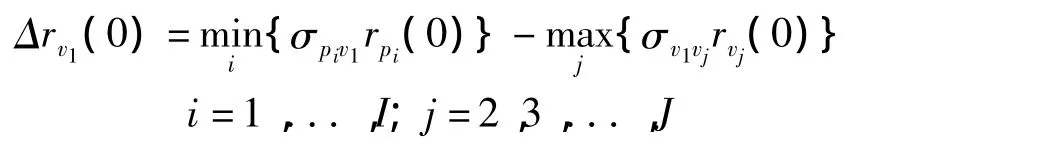
这里，Δrv1指政府购买v1的被替代率;

σv1pi指政府购买v1与第i种产品价格之间的固定替代弹性值，i=1，...，I;

rpi(0)指第 i种产品价格的增长率，i=1，...，I;

σv1vj指政府购买v1与第j种其他约束条件之间的固定替代弹性值，j=2，3，...，J;

rvj(0)指第 j种其他约束条件的增长率，j=2，3，...，J。令:

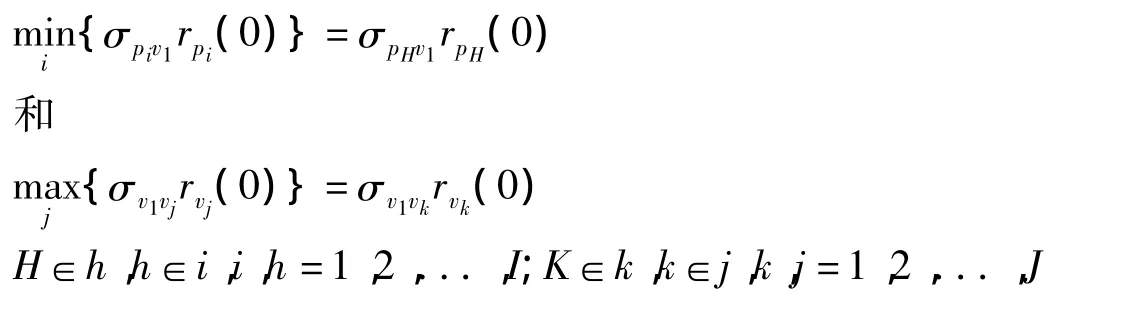
并得出:

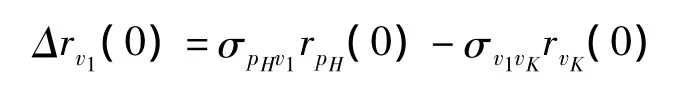
进而得到:

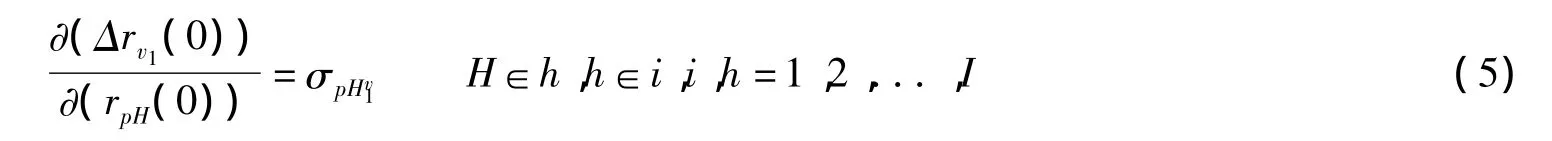
和

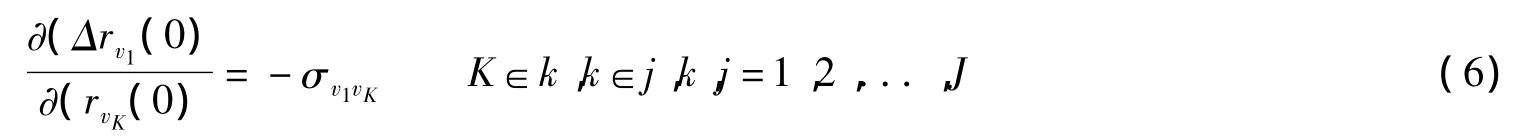
同理，得出转移支付v2的被替代率为:

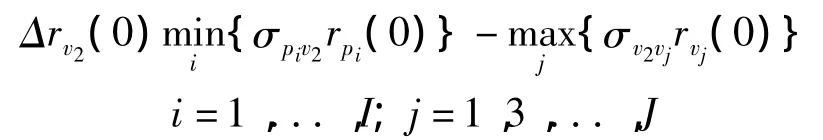
上式中，Δrv2是指转移支付v2的被替代率。其余因子的定义同上。

同样，令

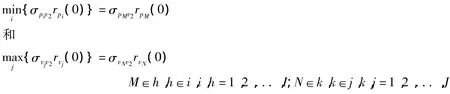
并得出:

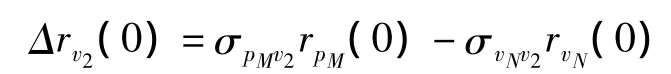
也进而得到:

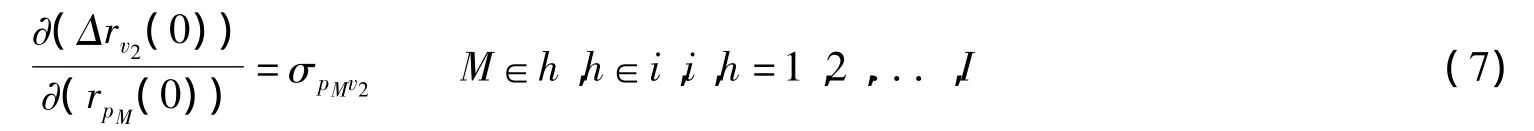
和

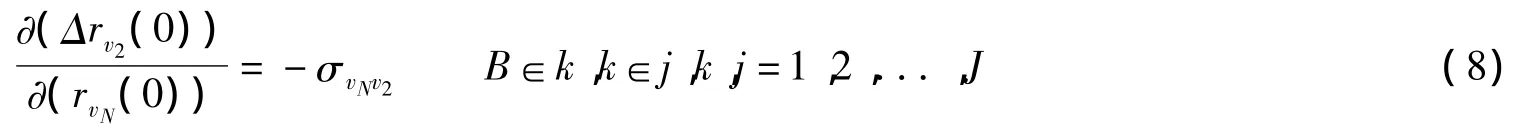
式(5)和式(6)所表明的是，在正则定律和经济容量最小缩减法则的作用下，政府购买v1的被替代率Δrv1(0)与直接决定它的第H个价格的增长率rpH(0)和第K个其他约束条件的增长率rvK(0)之间，分别存在乘数关系，相应的固定替代弹性值σpHv1和－σv1vK便分别是它们的乘数。同理，式(7)和式(8)所表明的是政府转移支付v2的被替代率Δrv2(0)与直接决定它的第M个价格的增长率rpM(0)和第N个其他约束条件的增长率rvN(0)之间存在的乘数关系，相应的固定替代弹性值σpMv2和－σvNv2便分别是它们的乘数。

式(5)－式(8)所给出的就是资源分配中关键活动和关键约束与经济容量之间的直接决定关系，它们之间的乘数或固定替代弹性值是经济结构进行调整的基础。它们可以成为宏观干预实施介入的参照，可以成为经济因子之间对干预作用实行传递的出发点［9］。并且，由此还可以看出，经济系统里的固定替代弹性值，便是经济因子之间相互由增长率传递为被替代率，或者反过来，由被替代率传递为增长率的乘数或移动系数［10］。

三、讨论与结论

为便于阐述，在进行下列讨论之前，有必要指出，被替代率指数的负数，便是增长指数。相应的，负替代指数的被替代率实际上就是增长率［11］。

在t=0时，若出现了充分就业，决策变量f1和f2分别决定的政府购买v1和转移支付v2的变化为:∂(Δrv1(0))=e－βv1(f1，0)和 ∂(Δrv2(0))=e－βv2(f2，0)。这也就是说，出于充分就业的考虑，导致政府购买和转移支付出现了变化，即分别有了增长。这里的 e－βv1(f1，0)和 e－βv2(f2，0)分别为各自的增长率，其中，βv1(.)和 βv2(.)分别为各自的被替代指数。这也意味着，这时出现了对政府购买v1和转移支付v2的调控，有了调控值和，即有了:

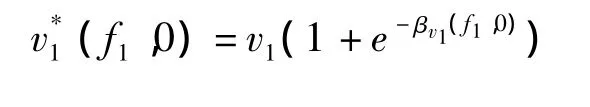
而这时，根据式(5)－式(8)，必然出现:

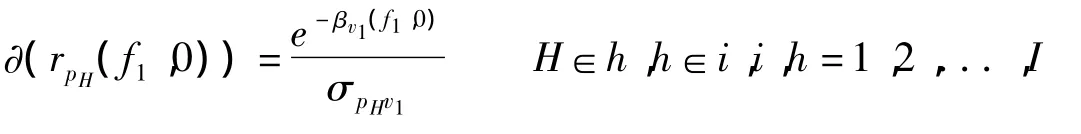
和

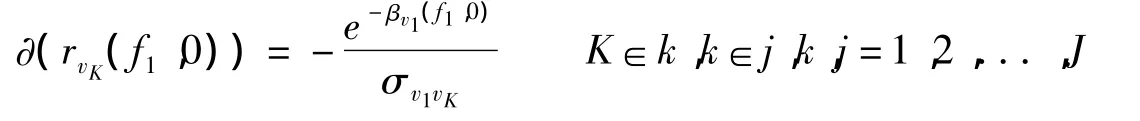
以及

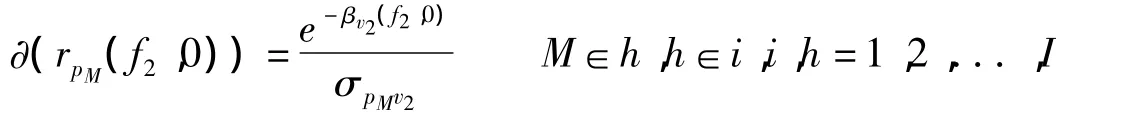
和

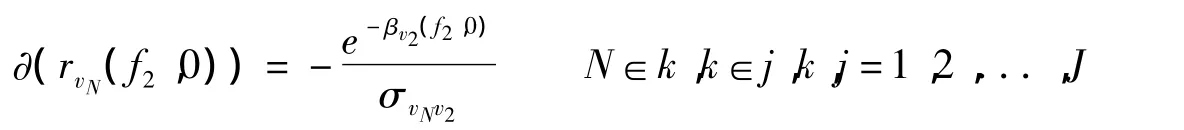
也就是说，随着政府购买和转移支付的变化，与购买直接联系的这个价格pH和其余一个约束条件vK会即刻发生增长;而与转移支付直接联系的这个价格pM和其余一个约束条件也会即刻发生增长。

这些价格的增长和约束的增长，会在经济内部传递到其他价格和约束上去，这就是通过价格之间和约束条件之间存在的固定替代弹性发生变换，并根据正则规律进行选择。于是，有:

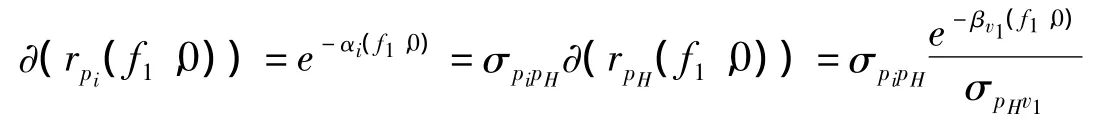
和

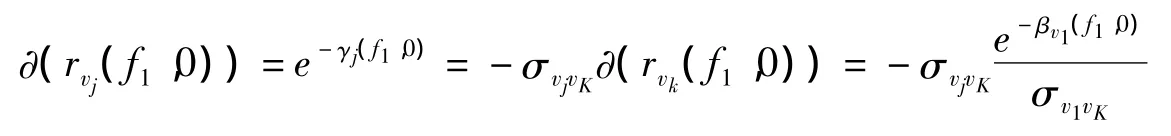
以及

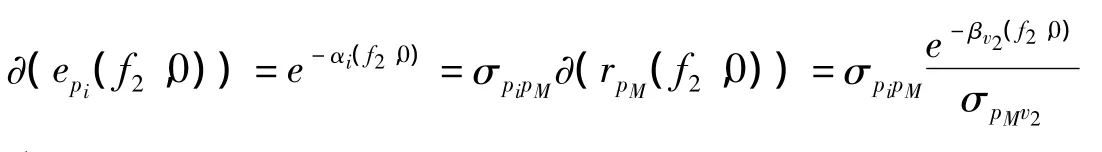
和

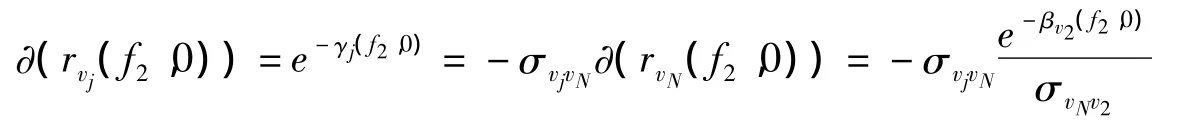
而根据正则规律和约束条件最小缩减法则，能够得出:

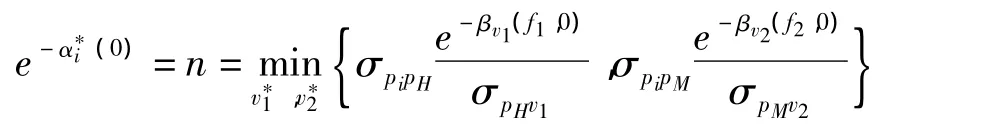
和

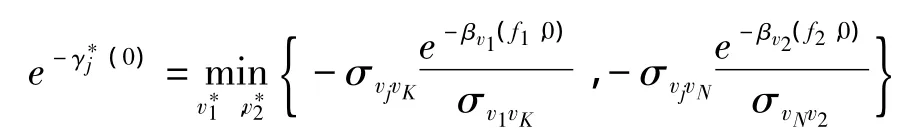
假定在经济运行中，这样的调整和传递会在t＞0的时刻完成。那么容易得出，这时应该有:

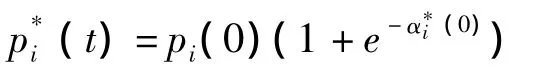
和

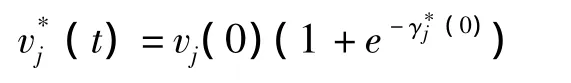
此刻可以得到的利润函数为:

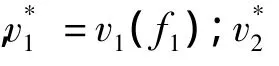
在式(9)里，由Hotelling引理可以得出第i种产品的预期供给量x*i(t)为:

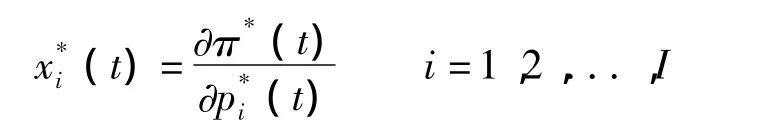
这时，各个产出的预期价值y*i(t)为:

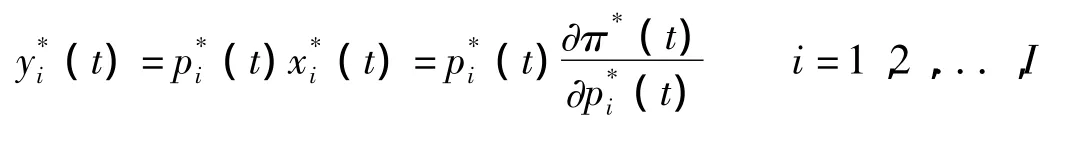
进而可以得到:

式(10)便是预期的国民收入。

但是，这时实际观测到的数据可能是:

π(p;v，t)

那么，根据Hotelling引理可以得出第i种产品的实际供给量xi(t)为:

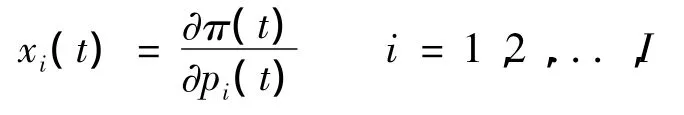
其价值yi(t)为:

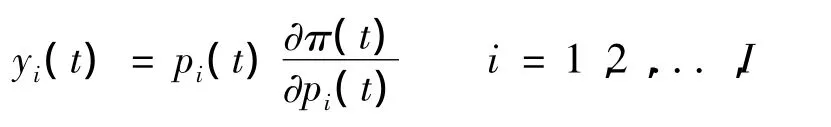
进而可以得出实际的国民收入y(t)为:

显然，有了式(10)和式(11)，便很容易求解布朗的“充分就业预算盈余”方程了。也就是很容易得出国民收入预期了，并且，也可以很容易地得出有关评估值了。从而，也就可以对有关财政政策的实际效果进行比较精确的评价了。

综合上述，可以得出下列三点主要结论:

(1)宏观干预导致国民收入发生变化是一种真实的存在。要做出理论探讨，在以往的经济学范式里，虽可推断，却因为难以作出有效的初始陈述，而不得深入和精确，因此，只可默认其概念，而不能理解其规律。在最新的经济学理论范式G函数里，实现有关初始陈述已经是很容易的［12］。继而借助正则规律、固定替代弹性法则和Hotelling引理等得出有关测度，从而对这种真实给予精确地解释，也是比较容易的。

(2)事实表明，在现代经济管理工作中，财政政策已经成为日益重要的宏观干预手段之一，运用财政政策来调控经济已经越来越普遍，其效果也越来越明显［13］。然而，由于以往的经济学范式难以对此作出精确化的解释，致使对这种调控的预期效果，始终没有在理论方面得到有效的解释，更没有在计量方面取得实质性进展［14］。运用G函数继续进行探索，得出更加深入的理论解释和更加精确的测度，不仅会更有力地促进经济学理论的进步，还会更有力地推动有关计量技术的进展。

3)财政调控与国民收入是经济运行中的一对明显的对应，要使有关财政政策，例如出于充分就业而考虑到政府购买和转移支付应有所改变，那么，就有必要以预期的国民收入作为参照。而对这个预期进行精确化的分析，似乎更是必不可少。因为它的精确测度，不仅会清晰地揭示其本身，令人明了有关政策的方向;还会清晰地解释整体经济的结构变化，令人加深科学的认识［15］。这样的揭示和解释，对于经济学理论的发展和对于实际经济管理工作的开展，都是值得重视的。

［1］BAUMOL B，BLINDER J.Economics——Principle and Policy(7th)［M］.New York:Dryden Press，1997:104－106.

［2］高鸿业.西方经济学(宏观部分)第五版［M］.北京:中国人民大学出版社，2011:464.

［3］李西林.G函数与现代经济学派分析［J］，汕头大学学报(人文社会科学版)，2008(1):10－14.

［4］SAMUELSON P.Foundations of Economic Analysis［M］.Cambridge，MA:Harvard University Press，1947:103 －105.

［5］孙中才.G函数与经济学的新进展［J］.汕头大学学报(人文社会科学版)，2006(6):20－24.

［6］GORMAN W.Measuring the Quantities of Fixed Factors［C］.Wolfe J N.Value，Capital and Growth:Papers in Honor of Sir John Hicks，Chicago:Aldine Publishing Co.1968:141 －143.

［7］孙中才.通货膨胀与宏观调控［J］.山东财政学院学报，2012(4):5－11.

［8］DIEWRT W E.Functional Forms for Profit and Transformation Functions［J］.Journal of Economic Theory，1973(6):284 －286.

［9］孙中才.农业系统工程(上)［G］.北京:中国人民大学出版社，1987:79－80.

［10］孙中才.宏观干预与通货膨胀［J］，汕头大学学报(人文社会科学版)，2011(6):34－41.

［11］孙中才.货币运营与通货膨胀［J］，山东财政学院学报，2013(1):51－58.

［12］McFADDEN D.Cost，Revenue，and Profit Functions［C］//FUSS M，McFADDEN D.Production Economics:A Dual Approach to Theory and Applications，North－Holland Publishing Company:Amsterdam·New York·Oxford，1978(1):227－228.

［13］MOBIUS M，FENICHELL S.Passport to Profits，Why the Investment Windfalls Will be Found Abroad and How to Grab Your Share［M］.Grand Central Publishing，1999:72－74.

［14］原宇，夏慧.金融学基础［M］.北京:科学出版社，2010:68－74.

［15］［美］米什金 F.货币金融学［M］.刘毅，蒋理，王秀萍，等，译.北京:中国人民大学出版社，2005，93－95.