空间连杆机构中运动要素的图解与计算
田福润,陶 冶,陈 光
(1.长春工程学院机电工程学院,长春130012;2.华南农业大学工程学院,广州510642)
0 前言
在汽车、农业机械、飞机等产品设计中,常常遇到空间机构的复杂轨迹、极限位置、动点位移、运动速度、加速度等问题。
探讨以上问题对于设计新机构及分析现有机构都是重要的。如确定机壳形状和检查构件是否碰撞等,必须确定构件上某点运动轨迹及运动件的极限位置。又如分析构件的磨损与寿命,则必须研究有关构件运动速度及加速度等。本文采用画法几何方法图解与计算其中位移、速度等运动要素。
1 图解与计算
图1是空间连杆机构的简图,AB是主动曲柄,在V面内饶垂直于V面的轴做均匀旋转运动。旋转半径为AB,从动杆CD由于连杆BC的带动在H面内绕垂于H面的轴摆动,摆动半径为CD。B、C两处为球面副,A、D 两处为 回转副。H、V 两平面夹角90°。
设AB=R1,BC=L,CD =R2,A、D两点纵向距离为s,高度方向距离为h。AB杆的角速度为ω1。现确定CD杆的位移、角速度,点C的速度。
1.1 确定空间连杆机构中从动杆的位移
1.1.1 图解
如图2所示,根据已知的R1、L、R2、s、h及AB杆的位置α1,求BC杆的α2。
根据h、s确定2个圆心a′、d。并以半径R1及R2画出2个圆。据α1,确定点B(b、b′)。再以L为半径,b′点为圆心画弧交X轴于c1点,再以b为圆心,bc1为半径画弧交R2圆于c点。连cd则α2可确定。
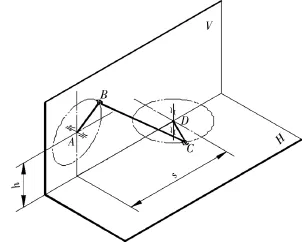
图1 空间连杆机构简图
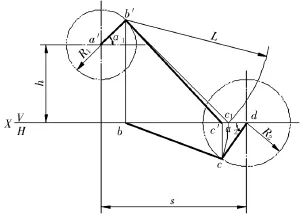
图2 空间连杆机构的投影
1.1.2 计算α2
由Rt△bb′c1可知
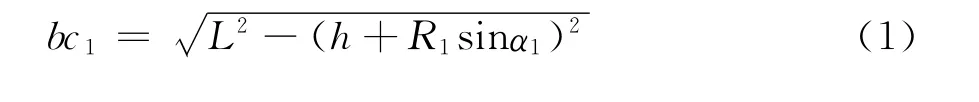
设以b为原点,bb′为Y轴,bd为X轴,点C坐标为(x,y),则cc1弧的方程为
R2圆的方程为
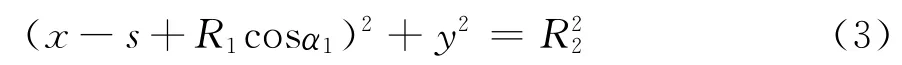
联立式(2)与式(3)得
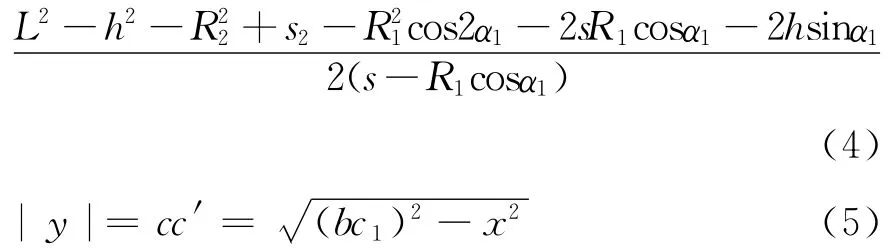
由式(1)得出bc1,由式(4)得x,于是得出y。
由Rt△cc′d 可知

由式(5)得出y,R2为已知,则α2可得出。
1.2 确定空间连杆机构中的速度
如图2所示,给定R1、L、R2、s、α1、α2、h及AB 杆的角速度ω1。确定点C的瞬时速度Vc、CD杆的角速度ω2,以及BC杆的角速度ωCB。
1.2.1 分析
根据相对运动原理,刚体(如连杆BC)上某点(如点C)的运动,可以看成刚体上任一点(如点B)的牵连运动和某点(点C)绕此任一点(点B)的相对转动之合成(图3)。其速度关系可写成
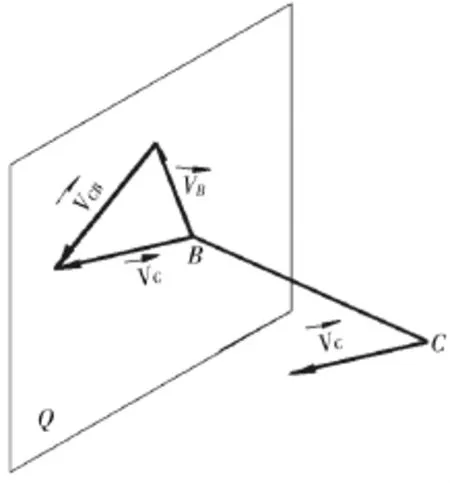
图3 运动的合成
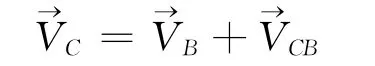
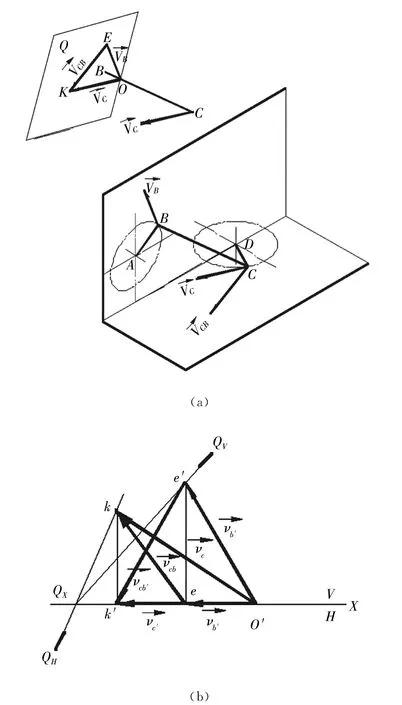
图4 运动速度的关系
1.2.2 图解
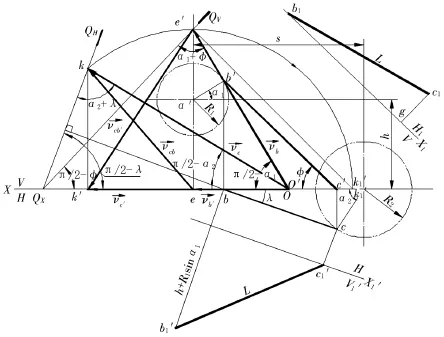
图5 速度向量图
过点E取旋转轴垂直于H面,将点K绕该轴旋转到K1,则e′k1′为EK直线的实长,即
根据BC杆长L,计算BC杆的投影长度。为此,先根据BC杆的V面投影b′c′和H面投影bc作一次换面,即作X1∥b′c′,b1c1为实长L。由Rt△b1c1g看出
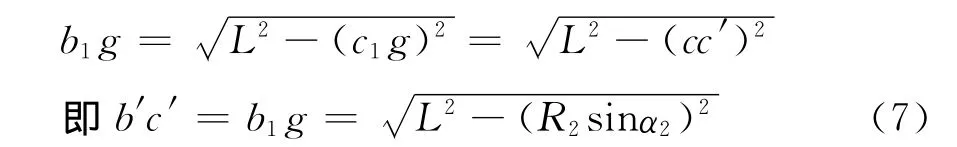
同理,作X1′∥bc,得
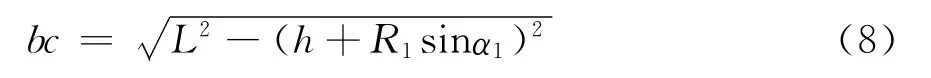
求BC杆长投影b′c′与X轴夹角φ及bc与X轴夹角λ。由Rt△c′bb′看出
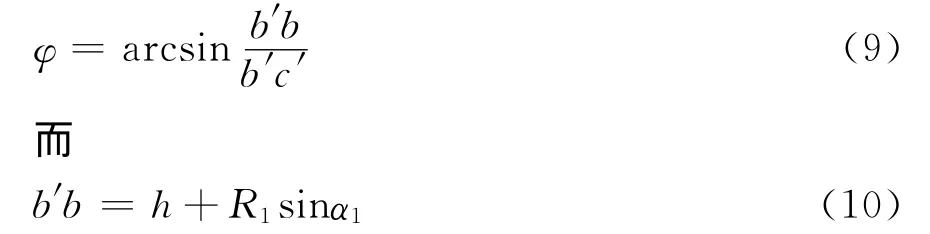
将式(7)、(10)代入式(9)得
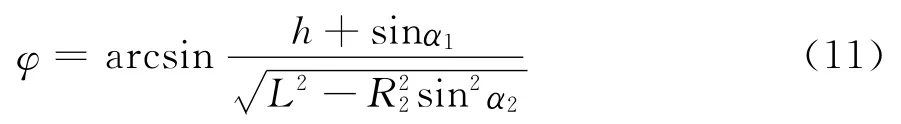
由 Rt△bc′c看出
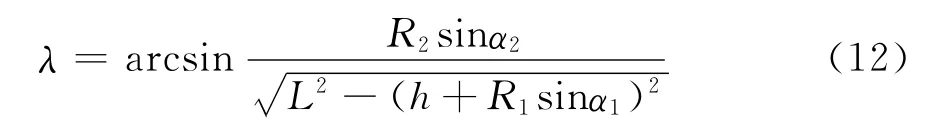
由 △Qxe′o′中看出
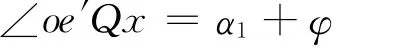
根据正弦定律有
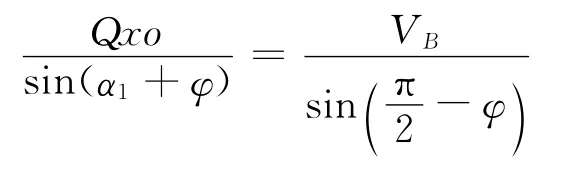
由于VB=R1ω1,故
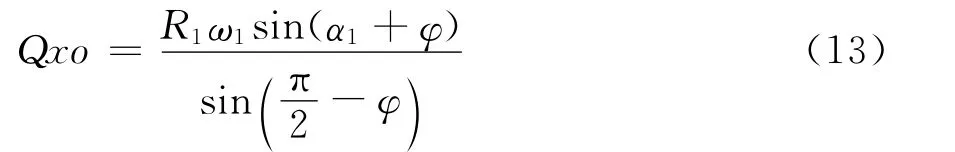
由△Qxko中看出
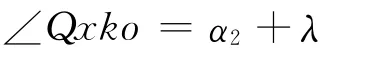
根据正弦定律有
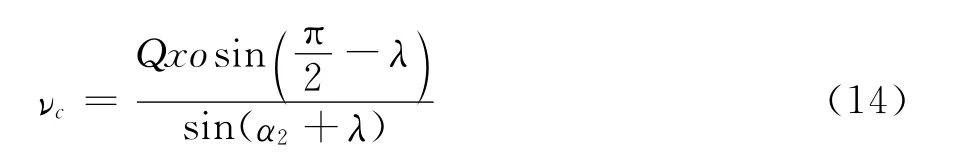
将式(13)代入式(14)有
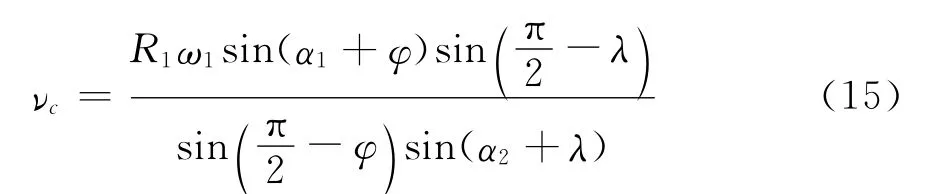
于是CD杆的角速度

根据已知条件,按公式(11)、(12)算出φ、λ,再按公式(15)、(16)可算出Vc及ω2。
计算BC杆的角速度ωCB
由直角三角形kk′o看出
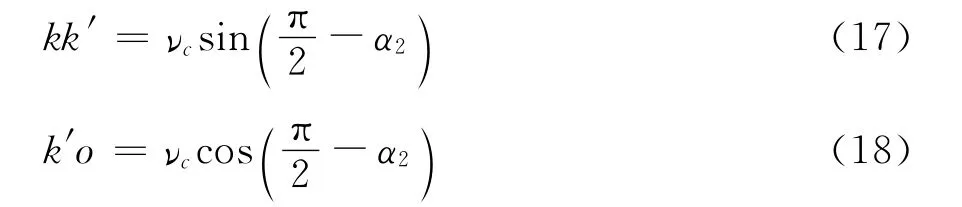
由Rt△ee′o看出

而

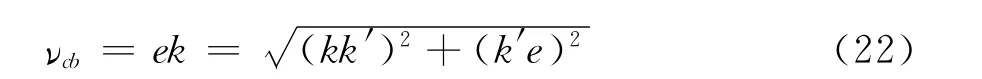
将式(17)、(21)代入式(22)有
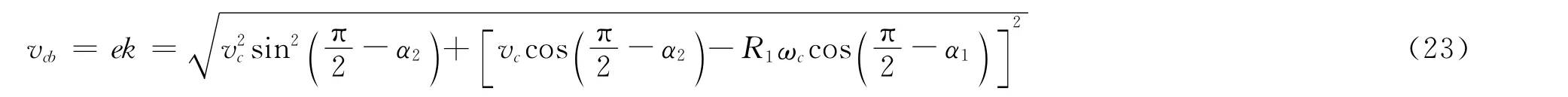
K旋转到K1时的大小
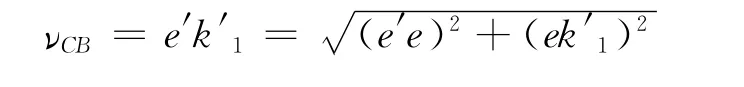

将式(20)、(23)代入式(24)得
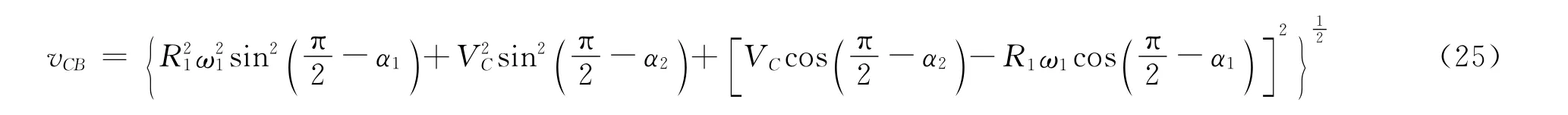
若已知R1、ω1、α1、α2,并由公式(15)算出Vc,则可按公式(25)确定νCB。于是BC杆的角速度

2 结语
采用画法几何图解与计算方法对空间连杆机构中运动要素图解与计算,能准确地确定空间连杆机构中从动杆的位移与速度,这种将空间问题转化成平面问题的方法使问题简化,很方便地对机构各部分尺寸参数加以调整,使之达到理想状态,任何空间问题均可以用画法几何的基本原理将其转换成平面问题加以讨论,这里仅讨论了位移、速度和角速度,关于角加速度还有待于探讨。
[1]刘文华.图解与计算在机械工程中的应用[M].长春:吉林人民出版社,2002.
[2]何在洲,张华第.连杆机构运动空间计算[J].机械研究与应用,2003,16(1):40-41.
[3]孙桓,陈作模,葛文杰.机械原理[M].北京:高等教育出版社,2006.

