大功率风电机变桨距减速器刚柔耦合动力学仿真分析

何卫东，李小龙，卢琦

(大连交通大学机械工程学院，辽宁大连116028)*

0 引言

国外大功率风力发电机变桨距减速器主要有两种形式:多级渐开线齿轮行星减速器和二级摆线针轮行星减速器.新型摆线针轮传动具有体积小、质量轻、传动比范围大、传动效率高、同时啮合齿数多、传动平稳、噪声小等诸多优点［1］.但由于国外技术封锁，我国目前只能使用三级渐开线齿轮行星减速器.对于二级摆线针轮行星减速器的研究是十分必要的.

在减速器传动过程中，摆线轮的运动形式是既有自转又有围绕偏心轴进行公转，其与针齿啮合时的微小变形在其大范围高速运动时对系统的动力学特性会产生很大的影响［2］.所以只对减速器进行多刚体动力学分析是不够的.本文以刚柔耦合动力学理论为基础，以Pro/E，ANSYS和ADAMS为建模平台，建立摆线轮为柔性体的刚柔耦合动力学模型，研究其动力学特性，为减速器的优化设计提供理论依据.

1 Craig-Bampton模态综合理论

Adams/Flex的原理是基于子结构模态综合(Componet Mode Syntheses，CMS)的固定交界面(Craig-Bampton)法建立的，该方法的基本思想是赋予柔性体一个模态集，采用模态展开法，用模态向量和模态坐标的线性组合表示物体的弹性位移，通过计算每一时刻物体的弹性位移来描述其变形行为［3］.在固定交界面法中，令子结构r交界面完全固定，并建立如下模态矩阵［Φ］r［4］:

式中，ΦIN为主模态矩阵;ΦIC为约束模态矩阵，可通过静态平衡关系求得.

主模态qN是交界面完全固定时所对应的固有模态(ωN≠0)，其与内部自由度μI一一对应;而约束模态qC是指依次释放每一个边界自由度，使其产生单位位移而形成的静位移分布所构成的静态模态(ωC=0)，约束模态qC与约束自由度μB一一对应，则有:

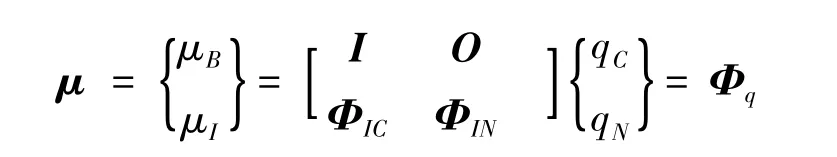
式中，I，O分别为单位阵和零矩阵;μ为位移矩阵.

利用模态矩阵Φ对质量和刚度阵进行第一次坐标变换(静凝聚变换)，得到模态坐标系的质量阵和刚度阵

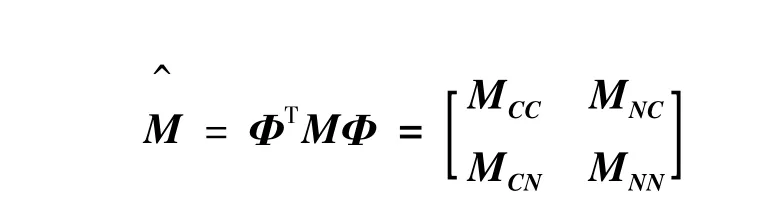
上两式中下标I、B、N、C分别表示内部自由度、边界自由度、正交模态和约束模态.

得到柔性体的动力学方程为:

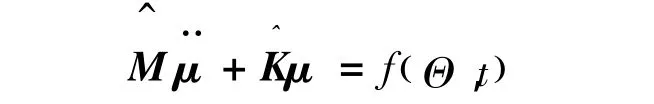
式中，f(Θ，t)为模态力，Θ为多体系统状态变量.

ADAMS中柔性体通过包含模态信息的模态中性文件(Modal NeutralFile，MNF)实现.MNF 文件中包含如下信息:几何信息(节点位置及其连接);节点质量和惯量;模态;模态质量和模态刚度.MNF文件通过有限元模型(Finite Element Model，FEM)软件 ANSYS、NASTRAN、I-DEAS 等分析转换得到.本文使用的是ANSYS软件.在ADAMS/Flex模块中对MNF文件进行静凝聚和正则化两次坐标变换，建立刚柔耦合系统的动力学方程.

2 减速器虚拟样机的建立

利用Pro/E三维实体建模软件，建立减速器的几何模型.装配后对其进行干涉检查，确定为无干涉装配.通过Pro/E与ADAMS之间的接口文件Parasolid(*.x_t格式)，将几何模型导入到ADAMS中.二级摆线针轮行星减速器虚拟样机几何模型如图1所示.

图1 虚拟样机几何模型

在ADAMS中对导入后的模型进行材料属性定义，模型简化和约束定义.根据实际情况，将各零部件的材料定义为steel.对于与传动无关的部件通过布尔加运算定义为一个部件(机壳)，对于和输入轴，中间轴，输出轴固定的各部件，分别与输入轴，中间轴，输出轴布尔加.根据减速器运动原理对简化后的模型添加约束，负载和驱动.为了避免数值突变，微分值不连续的情况发生，根据工况，利用step函数定义驱动为:

r(time)=2850d*step(time，0，0，1，1);

同理，定义负载函数为:

f(time)=step(time，1，0，2，－ 75000000)

根据文献［5］钢材料的碰撞参数，设置接触力的各参数为:Body1、Body2均为steel，k=105;c=50.00;E=1.5;d=0.1 mm;vs=0.1 mm;vd=10 mm;μ =0.3;μd=0.25. 利用Pro/E 与 ANSYS的接口文件，将一、二级摆线轮的几何模型导入到有限元分析软件ANSYS中.采用SOLID185单元对摆线轮划分网格，材料的密度为7.85×10－6kg/mm3，弹性模量为2.06 ×105MPa，泊松比为0.29.定义联接点和刚性区域，如图2所示.

图2 摆线轮柔性化

生成MNF文件后，利用ADAMS/Flex对其优化［6］.

在ADAMS中导入MNF文件生成柔性体.将原各级摆线轮设置为哑物体，令柔性体与哑物体固定，完成柔性体的添加.减速器刚柔耦合虚拟样机模型如图3所示.

图3 刚柔耦合动力学模型

3 仿真结果分析

3.1 摆线轮与针齿啮合力理论值计算

标准齿形摆线轮与针齿进行理论上的无间隙啮合时啮合力如图4所示，设第i个针齿作用在摆线轮上的力为Fi，其中在力臂最大位置的针齿与摆线轮之间的最大作用力为Fmax，其位置如图5所示.各齿受力Fi与相应的变形δi为线性关系，则有:

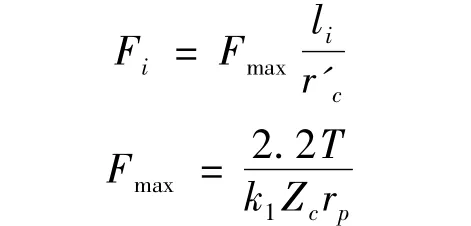
式中，li为第i个针齿啮合点的公法线至摆线轮oc的距离;T为输出轴上作用的转矩;k1为短幅系数;Zc为摆线轮齿数;rp为针齿中心圆半径.

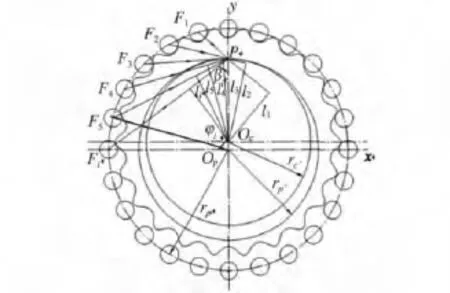
图4 针齿对摆线轮作用力示意图

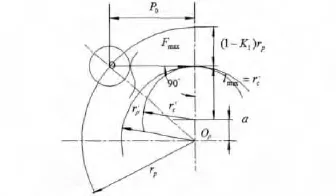
图5 受最大啮合力Fmax的针齿位置

摆线轮齿顶修型后与针轮进行有隙啮合，假设各齿与针齿沿待啮合点的法线方向存在的初始间隙为Δ(φ)i，且大小各不相同.此时各齿受力Fi与 δi－ Δ(φ)i为线性正比关系.则此时 Fmax的位置在φi=cos－1k1处的针齿，该齿最先接触受力且受力最大.则Fi和Fmax可表示为:

式中，δmax为在 φi=cos－1k1处，在 Fmax作用下，在接触点公法线方向总的接触变形;r'c为摆线轮节圆半径.

一、二级传动中摆线轮与针齿啮合力理论最大值分别为1 109.23、6 066.28 N;仿真最大值分别为 1 640、6 885、6 513.544 9 N.

3.2 虚拟样机各轴转速验证

对于仿真结果，首先验证虚拟样机的正确性.图6为输入轴，中间轴，输出轴转速曲线.根据一、二级传动比i1=11，i2=15，输入转速r1=475 r/min，得到中间轴，输出轴理论转速为r2=4.51 r/min 和 r3=0.301 r/min.

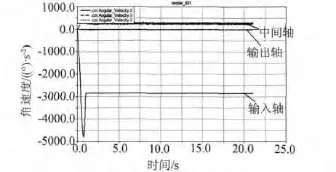
图6 各轴角速度曲线

附表为输入轴、中间轴和输出轴转速的仿真结果与理论值比较以及相对误差.

附表 转速，传动比验证

通过对比，可以得出仿真值与理论值的误差很小，并根据摆线针轮行星传动啮合原理［7］，中间轴与输入输出轴的转速方向相反.这点从仿真动画中也可以看出.综上所述，能够证明所建立的虚拟样机是正确的.

3.3 针齿与摆线轮啮合力仿真值与理论值比较

图7为一级传动中6号针齿与摆线轮1和2的啮合力幅值曲线.图中显示，6号针齿与两片摆线轮交替啮合，与实际相符.啮合力最大值为1640.688 5 N，比理论值1 109.23 N要大，这是由于在理论计算中，忽略了各零件的弹性变形同时也没有考虑柔性体摆线轮的振动对啮合力的影响.啮合力成周期性变化，各周期内幅值变化不大，说明啮合平稳，第一级传动具有良好的均载性和稳定性.

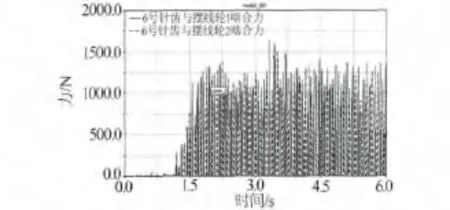
图7 6号针齿的啮合力曲线

3.4 刚柔耦合系统振动分析

图8(a)为多刚体系统中中间轴角加速度曲线，图8(b)为刚柔耦合系统中中间轴角加速度曲线.通过对比发现，各摆线轮考虑为柔性体后，振动明显增加，其振幅的平均值比多刚体系统中增大了一倍.各摆线轮与针齿啮合的微小变形在其大范围运动时对系统的动力学特性产生很大的影响，证明了前文假设的正确性.

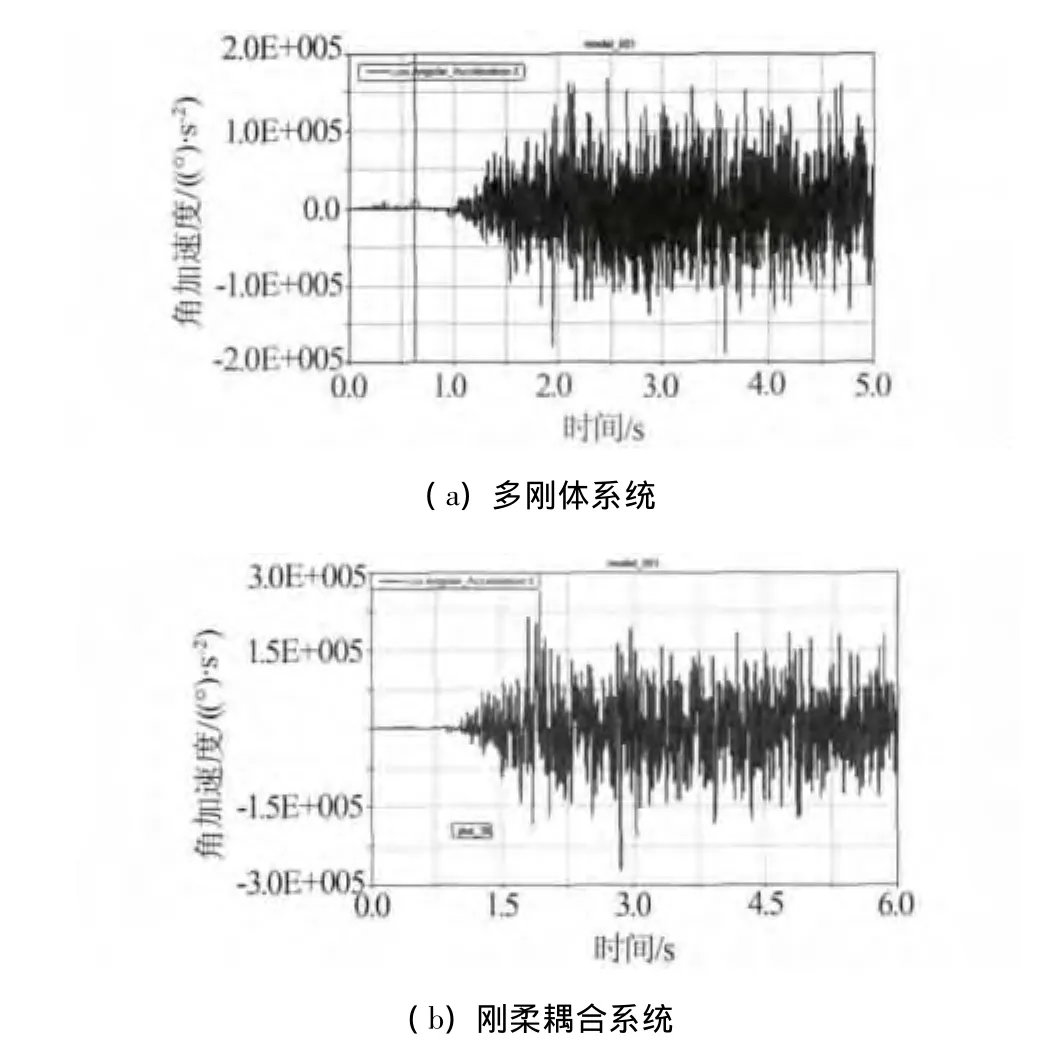
图8 不同系统中中间轴角加速度曲线

4 结论

基于刚柔耦合动力学理论，以多体系统动力学仿真分析软件ADAMS为仿真平台，建立了二级摆线针轮行星减速器的刚柔耦合动力学模型.经过分析，得到以下结论:

(1)通过对各级转速与理论值比较和接触力的理论值与仿真值比较，验证了所建立的刚柔耦合动力学模型的正确性;

(2)从一级传动中的6号针齿和与其接触的两片摆线轮啮合力曲线中可以得出，减速器啮合平稳，在传动过程中具有良好的均载性和稳定性;

(3)利用哑物体将柔性体摆线轮与系统联接，联接点为摆线轮质心;

(4)将摆线轮考虑为柔性体后，系统的振幅明显大于多刚体系统.参考文献:

［1］何卫东，李欣，李力行.高承载能力高传动效率新型针摆行星传动研究［J］.中国机械工程，2005，16(7):565-569.

［2］RYAN R R.Dynamics of Flexible Beams Undergoing Large Overall Motions［J］.J.Sound Vib，1995，181(2):261-278.

［3］殷学纲，陈淮，蹇开林.结构振动分析的子结构方法［M］.北京:中国铁道出版社，1991.

［4］朴明伟，丁彦闯，李繁，等.大型刚柔耦合车辆动力学系统仿真研究［J］.计算机集成制造系统，2008，5(14):875-881.

［5］陈萌.基于虚拟样机的接触碰撞动力学仿真研究［D］.武汉:华中科技大学，2003.

［6］赵丽娟，马永志.刚柔耦合系统建模与仿真关键技术研究［J］.计算机工程与应用，2010，46:243-248.

［7］朱孝录.机械传动设计手册［M］.北京:煤炭工业出版社，2007:683-689.