基于Workbench的高速压力机曲轴疲劳分析

衣 锐

（济南铸造锻压机械研究所有限公司，山东 济南250306）

0 前言

疲劳是结构失效的一种常见形式。结构在长期动力荷载作用下，其动力反应在小高的界限（低于或远低于首次破坏界限）上多次重复，最后由于累积损伤或裂纹扩张到某一界限而发生破坏。金属、塑料、木材、混凝等各种结构材料及其加工而成的结构或设备，在交变载荷的反复作用下，都会产生疲劳问题。高速压力机在工作状态下受到周期性的冲击载荷的作用，动载荷对压力机传动结构造成的影响和破坏往往大于静载荷。大量工程实际问题表明，结构的破坏往往源于动载荷，有时虽然未造成灾难性事故，也使得结构不能按所要求的性能正常工作。因此对于高速压力机，除了对主传动结构进行静态分析及动态响应分析之外，还需要进行主传动零部件疲劳可靠性分析，以了解零部件的结构在动载荷作用下的疲劳可靠性情况，以确保压力机的可靠性。曲轴是高速压力机传动系统中核心零部件之一，因此本文将对其进行疲劳寿命、损伤和安全系数分析。

1 理论基础

对于等幅加载，一般认为每一循环所造成的平均损伤为1/N，N 为该载荷下材料破坏前所经历的总循环数，则n 次循环所引起的损伤为n/N。对于变幅和随机加载，其疲劳破坏是不同频率和幅值的载荷所造成的损伤逐渐累积的结果。目前为止，己提出的疲劳累积损伤准则可分为四大类：线性疲劳累积损伤理论，双线性疲劳累积损伤理论，非线性疲劳累积损伤理论及其他疲劳累积损伤理论。

线性疲劳累积损伤理论假定材料在各个应力水平下的疲劳损伤是独立进行的且总损伤可以线性叠加。其中最有代表性的是Miner 法则[1]，Miner 法则提出任意应力范围产生的部分破坏与实际循环数对总循环数之间的比率成线性比例，试样所吸收的能量达到极限值时产生疲劳破坏。设材料破坏前可吸收的能量极限值为W，试样破坏前的总循环数为N，在等幅加载下，若试样经受的循环数为n1，吸收的能量为W1，则由于试样吸收的能量与循环数间存在着线性关系，因此有W1/W=n1/N。在程序加载下，若试样的加载历史由σ1，σ2，…，σm共m 个不同应力水平构成，各应力水平下的疲劳寿命依次为，各应力水平下的循环数依次为n1，n2，…，nm，吸收的能量为W1，W2，…，Wm，则当这些被吸收的能力达到极限值W 时，

上述方程描述了应力—应变寿命计算和局部应变疲劳寿命计算中的线性破坏状态。经验表明线性破坏的概括只是实际情况的简化。其主要的不足是未考虑加载顺序，并且该理论假设在任一给定的应力水平下，累积损伤的速度与以前的载荷历程无关，即对每一应力水平，不论在寿命的前期或后期，每次循环的损伤是相同的。但实际上出现在小应变幅之前的大应变幅会使小应变幅的破坏超过预想的效果[2-3]。实际的结果为前一种情况下，所测得Σ（F（n，N））值小于1，而后一种情况下，该值大于1。虽然如此，由于线性累积损伤定律简单，故仍在工程上得到了广泛的应用。

2 曲轴疲劳分析

2.1 材料的定义

由于疲劳可靠性分析是基于线性静力学分析，因此需要设定杨氏模量和泊松比；与静力学不同的是疲劳可靠性分析还需要定义材料的S-N 曲线。疲劳失效以前所经历的应力循环数称为疲劳寿命，一般用N 表示。结构的疲劳寿命取决于材料的力学性能和施加的应力水平。一般来说，材料的强度极限越高，外加的应力水平越低，试样的疲劳寿命就越长；反之，疲劳寿命就越短。表示这种外加应力水平和标准试样疲劳寿命之间关系的曲线，称为材料的S-N曲线[4-6]。S-N 曲线的左段一般是直线，其表示式为：

式中：m、C——均为材料常数。将上式两边取对数得：

由上式可见，S-N 曲线的左段在双对数坐标上为直线，1/m 为S-N 曲线的负斜率。用下式可以表示整条S-N 曲线：

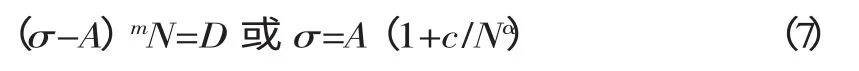
式中：1/m——S-N 曲线的负斜率；

A——材料的疲劳极限；

D——材料常数；

σ——S-N 曲线的负斜率；

C——材料常数。

2.2 曲轴载荷与约束的分析

与公称力F 相比惯性力较小，因此在对曲轴进行疲劳分析时可以忽略。曲轴左右两个曲柄分别承载50%的公称力，即50%F。又由于曲轴采用4 点支撑，因此曲轴载荷与约束如图1 所示。

图1 曲轴载荷与约束示意图

J78-80 高速压力机公称压力为800kN，而主滑块的惯性力不足公称力的5%，因此可以忽略不计。根据滑块冲程次数150～600min-1、公称压力行程3mm 和滑块行程30mm，可编制如图2 所示的脉冲载荷谱。由于此高速压力机是属于闭式双点结构型式，所以每点承载50%的公称力，即为400kN；因此，图中脉冲载荷的幅值为400kN。

图2 脉冲载荷谱

压力机曲轴、连杆、销轴的约束和载荷的定义如图3 所示。图中除了曲轴以外，其他为与曲轴配合零部件的简化模型。其中力A、B 所作用的模型是连杆的简化模型。并对其进行网格划分得到曲轴的有限元模型如图4 所示，节点205136 个，单元104368 个。

2.3 分析结果

根据上述简化模型，使用Workbench Fatigue Tool 对曲轴进行疲劳分析[7-10]。结果如图5 所示。其中图5a 为曲轴应力云图，最大应力88MPa，位于与连杆配合面两侧轴肩处。曲轴采用材料40Cr，材料许用静应力280MPa，相应安全系数3.18。图5b 为曲轴疲劳寿命云图，最小疲劳寿命已经超过109次，达到无限寿命，因此满足设计要求。图5c 为曲轴疲劳损伤云图，从图上可以看出，达到无限寿命时曲轴没有出现明显损伤。图5d 为曲轴疲劳安全系数云图，最低安全系数1.56，位于与连杆配合面两侧轴肩处。

图3 压力机曲轴约束与载荷的定义

图4 有限元模型

图5 曲轴疲劳分析结果

3 总结

基于Miner 线性累积损伤理论，根据设计要求编制了高速压力机核心零部件曲轴的载荷谱，使用Solidworks 创建曲轴的三维模型，运用Workbench 进行网格划分创建有限元模型，并使用疲劳分析模块Fatigue Tool 对其进行了疲劳分析。结果表明：在周期性冲击载荷作用下，曲轴的最小疲劳安全系数为1.56，疲劳寿命达到无限寿命，没有出现明显损伤现象。因此，曲轴满足疲劳设计要求。

[1]Miner M A.Cumulative damage in fatigue[J].Journal of Applied Mechanics，1945，67:A159-A164.

[2]张 涛，王克胜.应用Miner 法则进行齿轮寿命的预测[J].矿山机械，1994，5:23-26.

[3]王旭亮，聂 宏.考虑不同载荷顺序下应力损伤模糊性的Miner法则[J].南京航空航天大学学报（英文版），2008，25（3）：182-186.

[4]赵永翔，杨 冰.不完善概率疲劳S-N 曲线的Monte Carlo 修正[J].机械工程学报，2011，47（12）：170-174.

[5]傅惠民，刘成瑞.S-N 曲线和P-S-N 曲线小子样测试方法[J].机械强度，2006，28（4）：552-555.

[6]姚卫星.结构疲劳寿命分析[M].北京：国防工业出版社，2003:50-54.

[7]武秀根，郑百林，杨 青，等.疲劳累积损伤理论在曲轴疲劳分析中的应用[J].同济大学学报：自然科学版，2008，36（5）：655-658.

[8]秦为前，王栓虎，李太福，等.基于ANSYS 的压力机曲轴的有限元分析[J].煤矿机械，2011，32（9）：98-100.

[9]陈福玉，朱如鹏，王宇波，等.基于Workbench 的铆接连接件疲劳寿命的仿真分析[J].机械制造与自动化2011，40（4）：112-115.

[10]刘永峰，孙 宇，张新洲.基于ANSYS-PDS 的高速冲床曲轴可靠性分析[J].锻压技术，2012，37（5）：155-157.