小学数学教材使用的现状透视及解读策略研究*——以人教版小学数学教材为例

李成芳

(湖州市凤凰小学,浙江湖州 313000)

小学数学教材使用的现状透视及解读策略研究*
——以人教版小学数学教材为例

李成芳

(湖州市凤凰小学,浙江湖州 313000)

对教材进行解读研究是每个小学数学教师必备的基本能力。读懂教材是使用教材、有效教学的基础。但在教学实践中,仍存在诸多问题。因此,本文提出多视角解读教材的策略,即从编者角度去钻研教材,领会意图,把握特点;从学生角度去钻研教材,以人为本,贴近生活;从教师角度去钻研教材,发挥优势,活化教材。

小学;数学教材;现状;解读策略

教材是教师和学生进行教学活动的主要媒介,凝聚着众多专家、学者和数学教师的集体智慧。“课程和教材的知识”是教师学科教学知识的重要组成部分。教师对教材解读得是否全面、到位、深刻就意味其备课和上课的有效性。因此,读懂教材是每个小学数学教师必备的基本能力,也是创造性使用教材、有效教学的基础。

一、现象透视

在平时的教学研讨、调研以及教师访谈过程中发现,人教版教材在实施的过程中,有部分教师课前“吃”不透教材,课堂上徒留遗憾与尴尬,课后需要大量的补救和辅导,大大影响了数学教学质量的提升。[1]经过汇总分类,主要存在以下几种现象:

现象一:照本宣科式教学。许多教师则只会按照教材中例题所呈现的内容,活动方式一板一眼地实施照本宣科地开展教学,时常是教材说什么就教什么,教材写什么就做什么,以致教学任务无端加重,教学重心偏离教材本质。

现象二:走马观花式教学。人教版教材以学生的数学学习活动为主线,改变了原有教材以知识为主线的设计方式,强调学生的数学学习活动。而数学教师在一段时期内受浙教版教材的影响,思维被教材中所呈现的例题所禁锢,教学中过分注重教材的学习呈现形式,未能深入地了解教材的用意。

现象三:就事论事式教学。人教版教材从例题到练习的编排减少了知识点的简单重复,增加了知识点间的拓展与延伸,练习设计更贴近生活,更开放灵活。由于教师在教材解读过程中只关注教材例题呈现的单一知识点,而忽视教材试一试、练一练以及配套作业中相关知识点的展开,从而导致教学就事论事。

二、多视角解读教材的策略

要改变以上现象,提高课堂教学质量,首先要学会深度解读教材。深度解读教材时,教师要善于从“多视角”进行研读,不仅要从“编写者编”的角度,而且要从“学生的学”的角度解读,同时还要从“教师的教”的角度解读,从而更深入地把握教材,用好教材。

(一)从“编者编”的角度解读教材——尊重,读懂

编者在编写教材时,都经过精心设计、多次论证的。作为教师,首先应该对教材文本进行深度的研读和理解,解读“教材编写了什么”、“教材为什么这样编写”、“教材这样编写对教学有什么样的启示”,从而明确要“教什么”。读教材时要做到“四部曲”:

1.了解教材的整体结构

数学是一门系统性很强的学科,每一个知识点之间环环相扣,紧密联系,由此而组成一个具有严密逻辑性的结构;同时数学知识又有它的阶段性。因此,在钻研教材时,既要从全面出发,注意数学知识的系统性,又要注意数学知识的阶段性,特别要注意沟通各部分知识纵横两方面的联系。具体说,在钻研教材时要做到两想:(1)立足单元看全册,通过全册看整体,弄清整体与部分的关系,想怎样处理好各年级之间数学知识的衔接;(2)回到单元看知识点,想本单元的目标,在每节课,每个知识点,每个例题里怎样才能得到落实,才能达到宏观与微观的统一。

例如:三年级《小数的初步认识》这一教学内容,为了便于学生理解和掌握小数,人教版仍然采用了以往教材的编排体系,把小数划分为两个阶段教学。第一段安排在三年级下册,在学生初步认识分数的基础上认识两位小数,学习一些简单的小数加减法。第二段安排在四年级下册,在初步认识分数和小数的基础上,让学生开始系统学习小数;本学段还将学习小数的意义和性质以及小数的加、减法。小数的初步认识是建立在分数的基础上,同时又为四年级学习小数的意义打下坚实的基础。读懂了整体结构后,在教学“小数的初步认识”时就应当把握三点:一是本单元不要求离开现实背景和具体的量,抽象地讨论小数。二是小数的认、读、写,限于小数部分不超过两位的小数。三是简单的小数加减法原则上限于一位小数,并且结合元、角进行计算。读懂了教材整体结构及前后关系,那么对本节课的教学目标定位和教学设计就可以做到高屋建瓴。

2.明白例题的地位作用

例题是数学教材的核心内容,它具有规范性、典型性。通过例题的教学不仅可以使学生在掌握新知识的基础上构建新的认知结构,而且能由例及理,由例及法,由例及类,让学生举一反三,触类旁通。所以教师要舍得花工夫去研究所教例题在本节或本单元的作用。例如,《认识负数》这部分内容有这样一个例题:“小华从学校出发,沿东西方向走了2米,到了什么地方?”这一例题是通过形象化的图让学生解决“如果把向东走2米记作+2100米,那么向西走2米可记作什么?”这一问题的。书中用直观的图让学生观察、理解了位置关系,这不但有效地支持学生体会并理解抽象数的关系,而且也为初中理解数轴的特征作了初步的孕伏,此外也让学生再次体会日常生活中具有相反意义的量分别可以用正负数表示。因此,认真解读例题的内涵,对备课及教学设计极其重要。

3.发现习题的内在联系

习题是数学教材的重要组成部分,是学生进行有效学习的重要载体。习题在教材中的地位进次于例题,它能配合例题由知识转化为能力。如果缺少对习题的解读、重构和创新,就不能更好地发挥教材习题的功能,从而影响了课堂教学的效果。因此,用好教材的习题资源,是教师用好教材的一个重要部分。教师在解读教材时,首先应将教材上的全部习题演算一遍,并弄清下列几方面的问题:一是明确习题的目的要求;二是明确习题的重点;三是确定习题的解答方式;四是衡量习题的份量。五是选编补充题目。总之,教师在认真解读例题的基础上,要大力开发习题的资源,做到“小题大做”、“借题发挥”。让学生在教师精心设计的数学练习中触类旁通、观微知著、自醒自悟,让习题增值,达成学生对知识深刻的理解和灵活运用。

4.揣摩插图的编排意图

插图是数学教材的重要组成部分之一,插图旁还会出现指导思路、方法等的提示语和指明关键的旁注。它既是帮助教师正确使用教材,又是启发学生分析思考,掌握知识要领的学法指导。人教版教材通过游戏、对话、表格和图片等方式呈现教学内容,没有呈现结论,只有学生自主活动的建议和过程中的问题提示,力求为教与学留下尽可能大的探究和交流空间。教学的灵活性增加了,教师的选择空间扩大了。这些教材空间给教师教学带来一定的困惑和难度,同时也给主体间的有效合作带来了机会,让教师在使用教材时有更多的联想意境和创造空间。

例如:人教版第九册《解方程》这一内容,教材中采用了天平这一插图,而且在提示方法中只出示“用等式性质解方程”的方法。实际教学中,很多教师不理解,认为传统教材中用四则运算之间的关系解方程更容易教。如果联系课程标准以及中学教材进行研读和思考,就能发现插图的用意所在。“解方程”的目的不仅仅是为了找到“方程的解”,而是让学生理解等式的性质,会用等式的性质解简单的方程,有效实现从“算术”走向“代数”,突出了代数思维,更好地实现了中小学数学教学的衔接。同时,如果仍采用四则运算之间的关系解方程,就必须套用四则运算中的六个基本关系式,而“用等式性质解方程”,只要运用“等式的基本性质”进行解题,思路显得比较简单。因此,教师如果读懂、读透了插图,并善于在教材的“留白”处挖掘、拓展教材的深度和广度,就会使新课程教材真正成为有效激发学生的学习潜能、不断提高学生数学素养的“有效的信息资源”。

(二)从“学生学”的角度解读教材——研究,思透

学生是学习的主体,教材中的知识只有最终被学生所掌握,才能真正体现教材蕴含的数学价值。因此,解读教材不仅从编者的视角去解读,还应该从学生学的角度,再次走进教材,理解即将要学习的内容,体验学生学习的过程中会碰到什么困难,会有什么疑惑。。这样才能做到以学生为主体,体现学生的自主性。

1.找准学习起点

学生的起点有逻辑起点和现实起点。逻辑起点是指学生按照教材进度应该具有的知识基础和能力水平,它是编写者根据教材的逻辑结构和大多数学生的学习状况而预设的一种标准;现实起点是指学生经过学习后实际具备的相关知识、学习能力、思维水平等。显然,因为生活背景、家庭环境、心智水平等差异,不同的学生的现实起点是各不相同的。在教学活动的各个阶段,教师只有建立在真实的学习起点上,让逻辑起点和现实落点有效对接,才能有效提高教学效果。如教学人教版第九册“平行四边形的面积”一课前,研读时可以思考以下问题:学生已经学习长方形面积、正方形面积,这些认知基础能否有效产生正迁移?平行四边形的面积公式学生是否已经了解?学生的学习困难在哪里?教师如何提供有效帮助?于是,教师对40名五年级学生进行了一次前测,“你知道平行四边形的面积计算公式吗?请写出!”一问题中,有21名学生写“平行四边形面积=底×高”,占总人数的52.5%;有11名学生认为“平行四边形面积=边×边”,占总人数的27.5%。于是,教学时,教师就从这个问题出发,让学生表达自己的观点,然后教师引导:到底是哪个公式正确,请同学们自主验证!学生兴趣极高,通过验证、交流,学生不仅掌握了平行四边形的公式,同时也突破了难点。因此,解读教材时,还要正确把握教学起点,确定教学重点,可以为选择相应的教学策略奠定基础。

2.遵循学生认知规律

现代认知心理学研究指出:学生的学习过程从根本上讲是一个认知过程,即把教材知识结构转化成他们认知结构的过程。因此,教师在解读教材时,要注重遵循学生认知规律,从学生认知的特点、规律等出发,读懂教材,读透教材。例如:人教版第十一册《圆的周长》,从逻辑起点分析,学生还从未接触过圆周率,对于圆的周长是第一次接触。但实际上,许多学生对圆周率有所知晓。[3]一位老师是这样教学的:

(1).测量、计算、填空

师:圆的周长究竟与圆的直径有什么关系?下面咱们先做个实验,请大家先测量每个圆的直径和周长,再计算并填空。

学生测量,计算后汇报交流,教师板书如下:

直径是1厘米的圆周长约(3.14)厘米,圆的周长是直径的(3.14)倍;

直径是2厘米的圆周长约(6.28)厘米,圆的周长是直径的(3.14)倍;

直径是3厘米的圆周长约(9.43)厘米,圆的周长是直径的(3.14)倍;

直径是6厘米的圆周长约(18.86)厘米,圆的周长是直径的(3.15)倍……

(2).观察、比较、发现

师:仔细观察,分析以上信息,你发现了什么?

生:一个圆的周长总是它的直径的3倍多一些,大约是3.14倍。

在案例中,学生测量出3.14cm、6.28cm、9.43cm、18.86cm等这些“精确”的数据,试想,在刻度为毫米的直尺上可能测量出这些数据吗?显然,这些数据根本不是真实测量出来的数据。怎么会出现上述情况的呢?答案很显然,因为学生在学习圆的周长以前不是白纸一张,大部分孩子都已知道圆周率的概念,知晓∏≈3.14,他们测量出圆的直径后,又利用公式计算出圆的周长,然后把计算出的周长代替了测量出的周长进行汇报。更有甚者,为使数据更“像”是测量出的数据,有的学生还把计算出的数据进行适当改动,如“9.43cm”就是在计算出“9.42cm”的基础改动而成的。其实,这样的操作就是伪操作,在此基础上的推理即是伪推理。因此,在解读“圆周率”一课时,要遵循学生的认知规律,教学的目标的定位不是要让学生通过测量计算出圆的周长大约是直径的3.14倍,更为重要引导学生经历探究和思考,让学生通过数学的方法感悟到圆的周长是直径的三倍多一些,从而了解圆周率的发现过程,渗透数学思想与方法。

(三)从“教师教”的角度解读教材——创新,挖深

教学的组织者是教师,因此,在解读教材时,还要从自身的角度去钻研教材,发挥自身的特点和优势,活化教材。教师要“吃透教材”必须经过日积月累的学习和实践。教师在“吃透教材”的过程中也一定能使自己的教学理论、实践经验、个人素养得到不同程度的提升,达到师生共同提高的效果。教师研读教材应该“仔细体会,透彻理解,反复思考,问个究竟”。要注意提炼教材内容的本质,把握教材的重难点,仔细揣摩教材中提出的每一个问题等;要善于思考,多问几个为什么,如教材都呈现了哪些数学内容?为什么要这样呈现?根据教材内容我们需要安排哪些相关的数学活动?通过这些数学活动我们要解决哪些问题,达到什么目的?

1.立足难点的突破,挖掘教材的深度

在初步通读教材后,教师要围绕教材核心知识进行“追问式”阅读,即围绕教材核心知识追问自己几个问题,促进对知识的数学本质的理解,如概念的内涵与外延;公式、法则成立的条件和适应的范围,属于哪种知识类型,教材内隐的学习方式和数学思想方法等。例如:“认识面积”一课时,在初步通读教材后,我们提出了两个深入研究的问题,即“面积概念的本质是什么”“教材呈现4种不同的测量方法的意图是什么”,并通过查阅资料、阅读课程标准等多种方式进行研读。如关于面积概念的本质,《辞海》中的解释是:几何学的基本度量单位之一,是用以度量平面或曲面上一块区域大小的正数,通常以边长为单位长的正方形的面积为度量单位;也有相关研究文章这样描述:“面积作为一个概念,既表达一个动态的度量过程,又表达度量的结果”“面积作为一个相对的量,其意义表征模型既是离散的(用单位面积块去度量图形的面积),又是连续的(遇到一些不规则的图形时,可以把单位面积块继续划成更小的单位面积块进行度量)”。从研读中我们明确了面积概念的数学本质:面积跟长度、体积一样,都是一个度量概念;面积是用来刻画面的大小的度量单位;度量面积要确定一个标准作为面积单位,数学上通常以边长是“1”的正方形为单位面积;度量面、感受面的大小应成为建立面积概念的教学核心。

2.从有疑处出发,拓展教材的宽度

教学时应注重面积概念本质,淡化形式,不要过多地纠缠于概念的定义,专门刻意地设计一些环节去扣“物体表面”“封闭图形”这些字眼,而应该通过丰富的数学活动,比较面和平面图形的大小,引导学生感知面的存在和面的大小,丰富对面积的感性认识积累。同时,还要注意与周长概念的比较,促进学生面积概念的清晰建构。

例如:“植树问题”例3一课中,例题引用了围棋棋盘,求最外层一共有多少颗棋子;而笔者在教学时,却对例题进行了改编加工,改为“在正方形花坛最外层每边放5盆花,最外层一共可以摆放多少盆花”,引导学生探究。当引导发现规律:一共的盆数=(每边盆数-1)×边数时,一位学生孩子提出老师,我认为这个规律应该加一个条件,每边的个数不能是1。因为“1-1=0,0×4=0”,结果是0盆了。这些学生提出了一个深层次的问题:如果只讨论在正方形每边放1盆花,至少需要多少盆花?结果应该是2盆花(见图1);而本节课其实蕴涵了一个内在的条件,即每个顶点都要放。如果有这个先决条件,那每边至少需要摆2盆(见图2),而每边只摆一盆的情况是不存在的。因此,“一共的盆数=(每边盆数-1)×边数”这一规律就需要附加一个条件,即每边数量＞1。

由此再来深度地挖掘教材,我们不由地思考,教材借助围棋棋盘直接导入,是否有意而为之:其一,围棋的棋盘上都有格点,在其一周放棋子,不外乎一种摆法,即四个顶点都放,有意回避了其它摆法;其二,围棋棋盘是正方形,隐含了本节课重点讨论正多边形中的规律,从而回避了不等边图形中的规律。其三,围棋棋盘中每两个格点的距离都是相等的,从而回避了间隔距离不等的摆法;其四,围棋棋盘中,一般每个顶点处只放一个棋子,不存在叠放,所以正方形最多重复4个点。主题图的一个小小的改变,使得其中的内涵也发生了许多的变化,从而使教学目标也发生了变化。如果教师没有充分考虑到这些问题,就会出现一些尴尬的场面。因此,在对主题图进行再加工时,一定要理解教材本质,把握好拓展主题图的“度”,并在课堂生成中适时、灵活地引导学生思考,那不仅可以拓展学生的思维,拓宽教材的深度,同时也不会出现教师在课堂上尴尬的场面了。

图1 主题图一

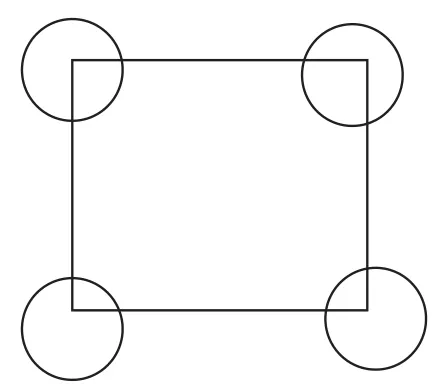
图2 主题图二

小学数学教师不仅是课程的执行者,更是课程的开发者和创造者。解读教材的目的是为了更好地创造性地使用好教材,教师首先要成为一部书,一部非常生动、丰富和深刻的教科书。这种专业自觉不仅是外界赋予的权利,也是教师教学生活的内在追求。

[1]张秋霞.解读教材,开发教材资源[J].教育研究与评论·小学教育教学,2010(12).

[2]郭艳芳.浅谈小学数学教材解读策略——以苏教版国标本小学数学教学为例[J].广西教育,2013(7).

[3]苏惠珍.合情推理不应被忽视[J].福建教育,2010(6).

Perspective and Interpretation Strategies on the Present Status in Using the Mathematics Textbooks for Elementary Schools——Taking PEP Primary Mathematics textbooks as an example

LI Cheng-fang
(Huzhou Fenghuang Primary School,Huzhou 313000,China)

Interpretation and research of textbooks is an essential basic skill for each elementary school teacher.Understanding textbooks is the basis of using textbooks and effective teaching.But in teaching practice,there are still many problems.Therefore,this paper proposes a multi-angle textbooks reading strategy.That is,from the perspective of the editors we should delve into textbooks,understand their intentions,and grasp the characteristics;from the perspective of pupils we should study textbooks,which should be people-oriented,and close to life;from the perspective of teachers,we should study textbooks,highlight the advantages and activate textbooks.

primary school;math textbooks;present situation;interpreting strategy

G624

A

1009-1734(2014)06-00100-05

2014-04-11

李成芳,小学高级教师,从事小学数学教育研究。