图例在概率论教学中的应用

祝慧敏,赵天玉 (长江大学信息与数学学院,湖北 荆州 434023)

图例在概率论教学中的应用

祝慧敏,赵天玉 (长江大学信息与数学学院,湖北 荆州 434023)

以蒙提霍尔悖论、事件间的关系和运算、正态分布、全概率公式等为例,具体阐述了教学过程中利用图例讲解概率论中的相关定义、性质和定理的教学方法,以帮助学生加强理解。实践表明,该方法不仅能够直观地揭示相关概念之间的关系,而且有利于提高学生兴趣,激发学生的思维,拓宽学生的解题思路,提高学生的解题能力。

概率论;图例;蒙提霍尔悖论;事件的关系和运算;韦恩图;正态分布;全概率公式

《概率论与数理统计》是我国高校的绝大部分工科、理科专业及管理类专业的一门重要的基础课程[1-2],也是应用性极强的一门学科,不仅在各个领域中具有广泛的应用,而且对人才素质的全面培养具有重要作用。进入21世纪之后,人们可以通过各种媒体获得越来越多的统计信息,这些信息传递着政府部门的重要政策取向,没有良好的数理统计知识就不可能很好地把握这些统计信息的特性,并善加运用。

概率论是对随机现象统计规律演绎的研究,但在学习概率论的相关知识时,学生总是反应概念粗象,难以理解。图例有着很好的直观性,可以帮助学生加强理解。为此,笔者在概率论的教学过程中,提出了利用图例讲解概率论中的相关定义、性质和定理的教学方法❶长江大学教学研究项目(JY2013026)。。

1 蒙提霍尔悖论

在概率论的第1节课,通过一个游戏来作开场白:先在黑板上画三扇门,并在门上标上1、2、3,如图1所示。然后对学生提出如下问题:这3扇门中其中有一扇门后面是车,另外2扇门后面是羊,假设猜中车就开走。现在请学生做选择,如果学生猜1号门,然后告诉他们2、3号门中2号(或3号)门后面是羊,问学生是否要换3号(或2号)门?这个时候学生的反应是分成2种的,一部分是换,一部分是不换(答案是换)。

这个游戏的名字叫蒙提霍尔悖论,也称为贝朗特箱子悖论。这个游戏非常有意思,即使老师把结果分析给学生之后,学生也会觉得不可思议,还会在课后进一步讨论。学生的学习兴趣一下子就被调动起来了。这个游戏就是通过在黑板上画图来表现的,非常直观。

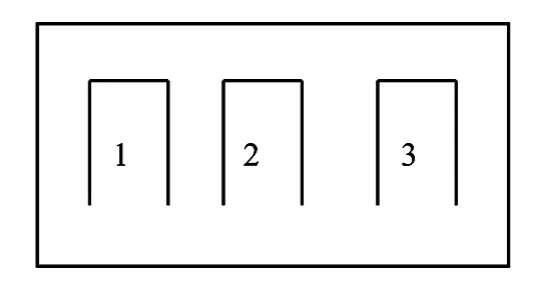
图1 蒙提霍尔悖论示意图

2 事件的关系和运算

其实在《概率论与数理统计》的大部分教材中,用集合论的关系和运算来刻画事件的关系和运算时,是用韦恩图来表示。

这一题很多教材上都有,关键是先分析出M、MN和M¯N之间的概率关系,然后再来解决后面的3个问题。书上是直接用集合的关系分析的,对于刚学概率的学生来说,这一步不太容易想到,如果用韦恩图的话,三者之间的关系就非常清楚了。

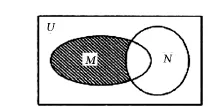
图2 事件关系韦恩图

3 正态分布

正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。单从正态分布的定义、概率密度上跟学生讲正态分布,学生听完之后对这个分布还不是很了解,根本不知道在日常生活中这个分布随处可见。画图3所示的正态分布图,告诉学生,只要符合“中间多,两头少”这种特点的都可认为是近似地服从正态分布的。如女生的身高,大多数是1.5m到1.7m,而低于1.5m和高于1.7m的占少数,符合上面这个图形的特点,所以身高就近似地服从正态分布。还有体重、考试成绩等等,都具有这个特点。

图3 正态分布图

4 全概率公式

在介绍全概率公式之前,要学习样本空间划分的概念。

定义1 设S为试验E的样本空间,为E的一组事件。若满足:

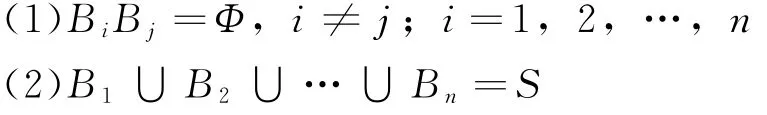
则称B1,B2,…,Bn为样本空间S的一个划分。

这个定义是比较抽象的,学生不太容易理解,但是在黑板上画出相应的图形,就很直观,学生也能一下子理解,如图4所示。从图4可以很明显的看到,样本空间被B1,B2,B3,B4分成了4块,即B1∪B2∪…∪Bn=S,满足定义的第2个条件。这4块彼此之间没有交集,也就是说B1,B2,B3, B4互不相容,满足定义的第1个条件。从而,图中的B1,B2,B3,B4就是样本空间的一个划分。

此外,教材上还强调样本空间的划分不唯一,这个也可以从图4表现出来,样本空间S可以用图4的几条线分成这4块,也可以用更多的线分成5块、6块,甚至更多块,所以划分是不唯一的。

在图4中再作一个圆,设为事件A,如图5所示。在图5中,这个圆可以看成由哪几部分组成呢?可以很明显的看到,圆A与 B1,B2,B3,B4分别相交,记为AB1,AB2,AB3,AB4。即A=AB1∪AB2∪AB3∪AB4且AB1,AB2,AB3,AB4这4部分互不相容,由概率的有限可加性有:

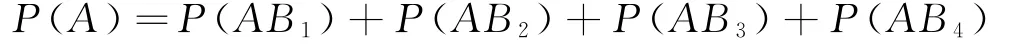
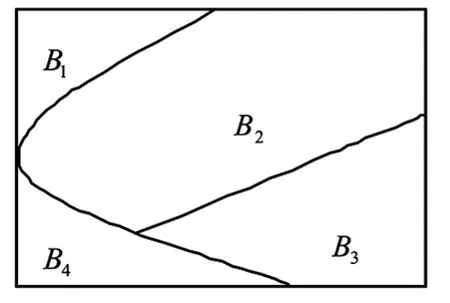
图4 样本空间划分图

图5中将样本空间分成了4块,以便于学生看得清楚。依次还可以推广,假设样本空间S被分成了B1,B2,…,Bn这n块,由上面的推导可以推出:

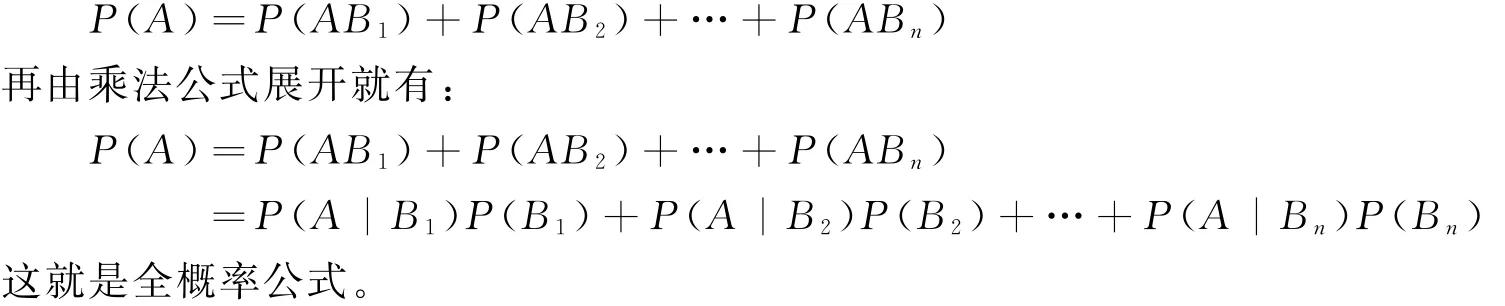
5 结语

通过上面的研究发现,先通过一个小游戏将学生的学习积极性调动起来,在接下来的教学过程中,将一些晦涩难懂的定义或性质用图形的方式在黑板上表现出来更直观,并且让学生更容易理解和接受,这样就能让各个专业的学生轻松、愉快的学好《概率论与数理统计》这门课程。

[1]李正耀,周德强.概率论与数理统计[M].北京:科学出版社,2009.

[2]魏宗舒.概率论与数理统计[M].北京:高等教育出版社,1983.

[编辑]张涛

N4;O211

A

16731409(2014)25012003

2014-02-14

祝慧敏(1979-),女,硕士,讲师,现主要从事应用数学方面的教学与研究工作。