利用半波带法计算单缝夫琅禾费衍射的光强分布
任振忠(晋中学院信息技术与工程学院 山西 晋中 030600)刘云龙 (聊城大学物理与信息工程学院 山东 聊城 252000 )
在大学物理的教学中,对于单缝夫琅禾费衍射一般是先用菲涅耳半波带法分析明暗条纹的分布,再用振幅矢量合成法来得到条纹的光强[1].菲涅耳半波带法简单直观,容易被学生所接受,可以很简单地给出暗条纹公式
这里a为缝宽,λ为正入射单缝的单色光波长,φ为衍射角.同时也得到了近似的明纹公式
但是菲涅耳半波带法存在明显的不足:不能给出明纹的光强,更不能得到观察屏上任一点的光强.在光学教程中,单缝夫琅禾费衍射的严格光强公式是根据惠更斯-菲涅尔原理,利用菲涅尔-基尔霍夫衍射积分公式得来的,但这种积分方法非常繁琐复杂.
1996年,文献[2]利用半波带,通过积分的方法求得单缝夫琅禾费衍射光强的严格解.本文从菲涅耳半波带法出发,结合矢量合成方法,得到单缝夫琅禾费衍射光强的分布公式.
为便于对比,这里给出单缝夫琅禾费衍射的严格光强公式[3]
式中
而I0是屏上中央明纹的光强.
假定对于某一衍射角φ,狭缝可分为m个半波带(m的取值可以是非整数),如图1,即
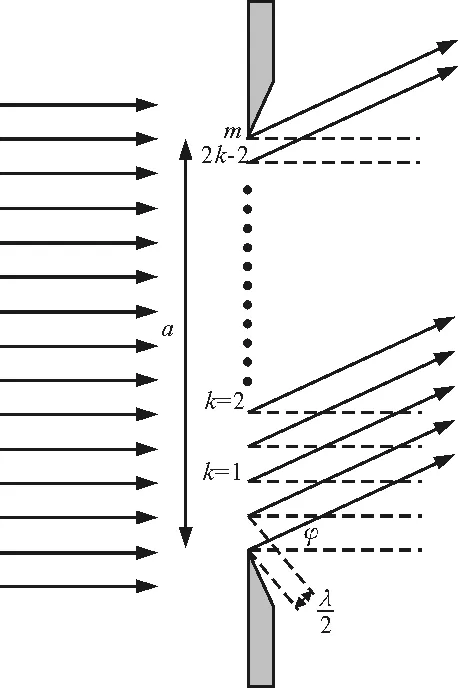
图1
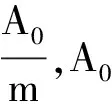
现在对剩余的这个波带进行分析.将其分成N个宽度为d的子波带[1](图2).根据惠更斯-菲涅耳原理,每一个子波带都可以看做是一个次波源.当衍射角比较小时,可假设由子波带发出的次波到达屏各点时,振幅相同,但相位依次相差一个相同的值
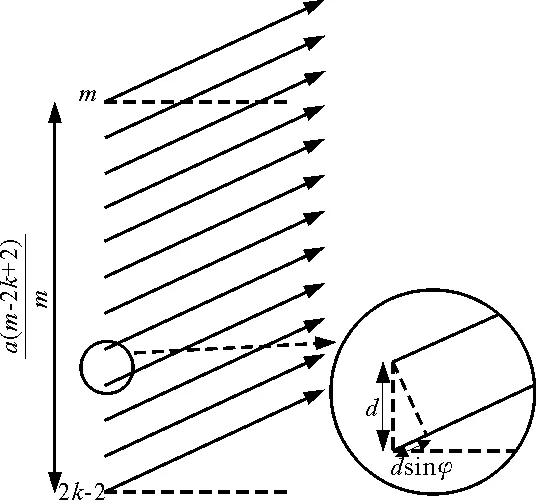
图2
在屏上形成的光振动可看做是同方向、同频率、等振幅,相位依次相差δ的N个次波形成的光振动的叠加.合振动振幅为
第一个光矢量E1与第N个光矢量EN的夹角为
当N很大时,光矢量叠加形成的多边形可认为是圆心在O,半径为R的一段圆弧(图3).
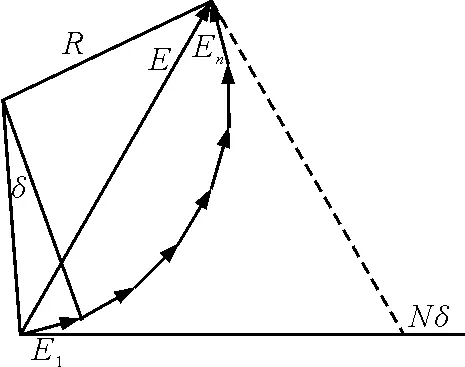
图3
从几何关系可得
即
式中
所得光强为
这与利用菲涅尔-基尔霍夫衍射积分公式计算得到的单缝夫琅禾费衍射光强的严格公式一致.
上面的分析中,从半波带的思想出发,通过矢量合成方法,精确地得到了单缝衍射光强公式,方法简单直观,物理内涵清晰.
参考文献
1 吴百诗.大学物理.西安:西安交通大学出版社,2009.127
2 薛天缘.半波带法讨论单缝夫琅禾费衍射的延伸.大学物理,1996,15(3):25
3 赵凯华,钟锡华.光学.北京:北京大学出版社,1984.212
Abstract:From the idea of Fresnel's zone, using the vector superposition method, the rigorous solution about the intensity of single-slit Fraunhofer diffraction is obtained.
Keywords:diffraction, half-wave zone, light intensity

