椭球体的视电阻率特征

张 超，汤井田，强建科

(中南大学 地球科学与信息物理学院， 长沙 410083)

0 前言

椭球体是最具代表性的典型三维地电体，它三个轴的长短变化后可以和多种形状的地电体相似，球体、柱体、椭球柱体及板状体都是椭球体的特例。因此实现了在常用场源激励下椭球体电阻率的求解，就可以模拟绝大多数三维地电体的电阻率曲线。

J．H．Webb[1]提出了通过镜像法推导均匀半空间点电流场中椭球体的精确解的思路[1];傅良魁等[2-3]研究了椭球类矿体(球体、圆柱体、椭球柱体)和椭球体的电阻率和形状对矿顶上方视电阻率异常值大小的作用规律;宋子齐[4]对椭球类矿体的电场和磁场进行了一般性讨论;雷林源[5]通过求解直角坐标系中的拉氏方程，导出了椭球位函数的一般形式，并通过边界条件和泊松公式，应用椭球位场的一般形式给出了均质椭球地质体和均匀磁化椭球地质体的重力位场和磁位场表达式;张秋光[6]详细推导了椭球坐标系下拉普拉斯方程的通解和均匀外磁场中的椭球体;罗延钟等[7]给出了直流电法中和频率域电法中倾斜旋转椭球体的视电阻率公式;强建科等[8]计算了椭球体复电阻率相应的幅频率并讨论了旋转椭球体的充电率、中心埋深和长轴倾角对幅频率异常和曲线形态的影响;徐淳宁等人[9]利用模拟电荷法对椭球体的电阻率曲线进行了数值计算;段长生[10]对不同场源的椭球异常进行了正演拟合反演并确定异常体的各模型参数。

1 均匀场中椭球体及板状体的视电阻率公式

1.1 椭球坐标系及其通解

对给定空间任意点P的直角坐标(x，y，z)，解以下关于t的三次方程

(1)

可以求得三个不同的实根λ、μ、ν，且λ>-c2>μ>-b2>ν>-a2，这三个根(λ、μ、ν)称为P点的椭球坐标。

图1 椭球坐标系示意图Fig．1 Schematic diagram of ellipsoid coordinate system

椭球坐标系中拉普拉斯方程为：

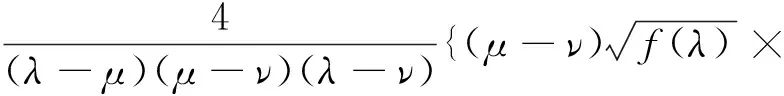
(2)

将公式(2)分离变量

φ=Λ(λ)Μ(μ)Ν(ν)

(3)

整理后可得到三个形式完全相同的拉梅函数，统一写为

(4)

我们可以用公式(5)表示椭球内部的拉普拉斯方程的解(有界)。

(5)

用式(6)表示椭球外部拉普拉斯方程的解。

(6)

1.2 均匀电场中椭球体的视电阻率

假设在电阻率为ρ1的均匀各向同性无限导电岩石中，有一个电阻率为ρ2，三个半轴分别为a、b、c的椭球体。取直角坐标系，原点位于椭球体中心，坐标轴X、Y、Z分别与a、b、c重合。均匀电流场的电流密度为j0，方向与X轴相同(见图2)。

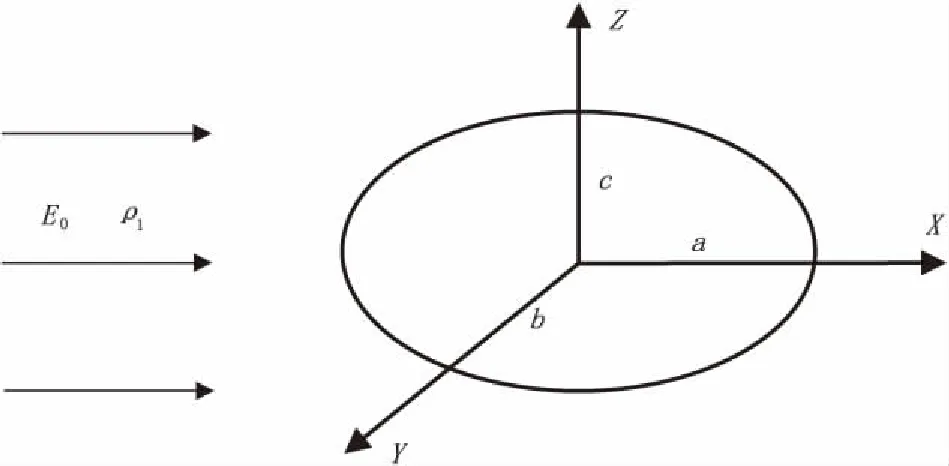
图2 均匀电流场中的椭球体Fig．2 Ellipsoid in uniform electric field

椭球体内、外的总场电位表达式：

(7)

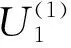
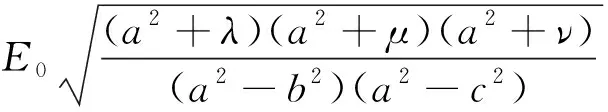
(8)

根据边界条件， 椭球体与围岩分界面上电位连续：

以及椭球体与围岩分界面上电流密度法向分量连续：

(9)

式(9)可变形为式(10)。

(10)

经过一系列计算与变量代换后，可得到椭球体内、外的总场电位为式(11)。

(11)

其中

L=2πabc·

(12)

L0=2πabcIx=2πabc·

(13)

(14)

均匀半空间情况下，采用将异常电位加倍的近似方法得到椭球体外部电位：

(15)

将E0=j0ρ1代入公式(9)得式(16)。

(16)

(17)

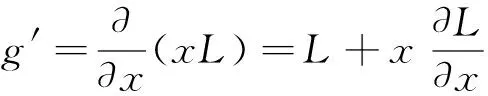
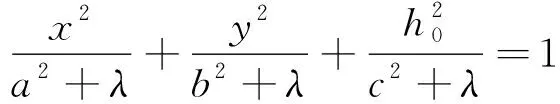
(18)

h0为椭球体中心埋深。

因此地面上沿x方向的视电阻率表达式为式(19)。

ρs=(1+2F1g′)ρ1

(19)

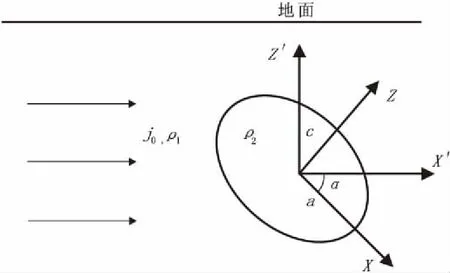
图3 均匀电流场中的倾斜椭球体Fig．3 Inclined ellipsoid in uniform electric field

1.3 均匀电场中倾斜椭球体的视电阻率

如图3所示为均匀电场中的倾斜椭球体。在求解倾斜椭球体时，用到了两套坐标系：XYZ坐标系-分别与椭球体的三个轴重叠；X′Y′Z′坐标系-X′的正方向与电流密度方向相同(即水平方向)，Z′的正方向垂直于水平地面，Y轴和Y′轴的正方向均垂直纸面向里。它们的转换关系为：

(20)

其中α为X轴逆时针旋转与X′轴的夹角，α∈[0,π)。

在推导出均匀电场中水平椭球体和直立椭球体的视电阻率公式之后，通过观察倾斜旋转椭球体公式的特点，导出倾斜椭球体的视电阻率的表达式：

ρs={1-2[Vx·R·cos2α+(Vx+Vz)·S·

sinα·cosα+Vz·T·sin2α]}ρ1

(21)

(22)

其中

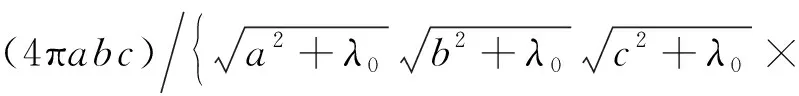
(23)

(24)

(25)

电性因子：

(26)

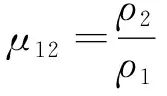
1.4 均匀场中的倾斜板状体

板状体由椭圆柱体近似得到。当b→∞，a远大于c(a≫c)时，可得到柱轴平行地面的椭球柱体的视电阻率表达式，公式仍有前式的形式，不过当中各因子都有所简化。

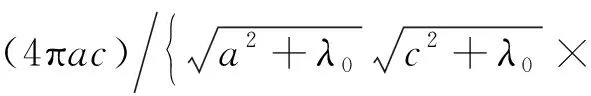
(27)

(28)

(29)

2 不同模型的视电阻率特征

2.1 旋转椭球体的视电阻率曲线特征

图4为低阻旋转椭球体的视电阻率曲线，模型参数为长轴a=10,两短轴b=c=2，中心埋深h=13。旋转椭球体分别沿顺时针旋转0°、30°、60°和90°。当低阻旋转椭球体水平或直立时，视电阻率曲线关于中心对称，且直立椭球体的极小值相比水平椭球体更小；当椭球体倾斜时，异常体顶部附近的视电阻率异常为零，在倾向一侧有极小值，在反倾向一侧有极大值，且倾角α越大，极大值越大；随着倾角α的增大，曲线逐渐变陡。

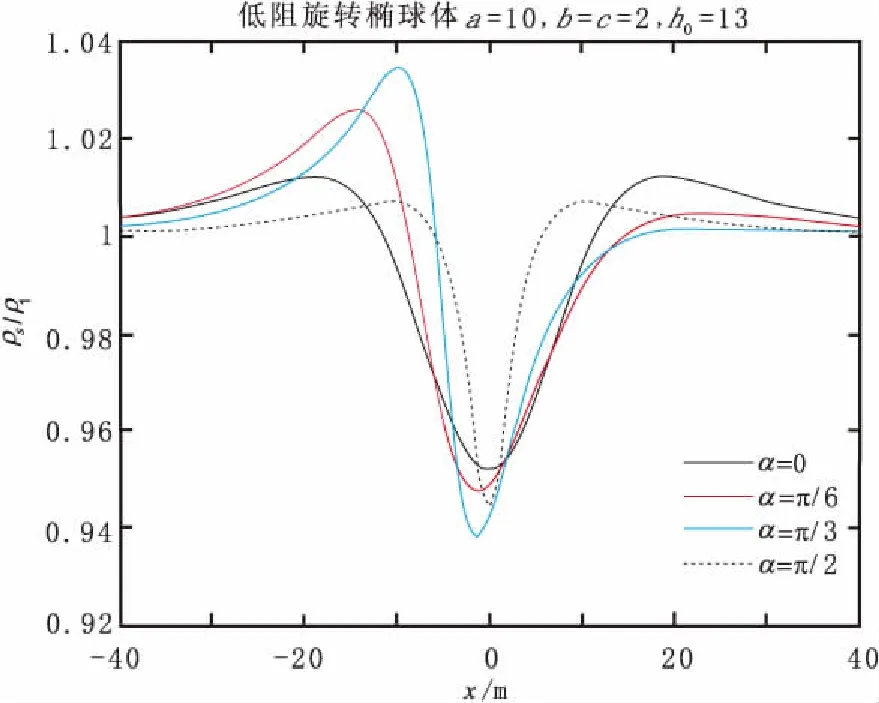
图4 低阻旋转椭球体的视电阻率曲线Fig．4 Apparent resistivity curve of rotating ellipsoid with low resistance

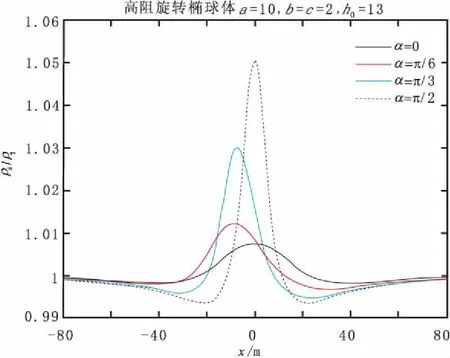
图5 高阻旋转椭球体的视电阻率曲线Fig．5 Apparent resistivity curve of rotating ellipsoid with high resistance

图5为高阻旋转椭球体的视电阻率曲线，模型参数为长轴a=10,两短轴b=c=2，中心埋深h=13。旋转椭球体分别沿顺时针旋转0°、30°、60°和 90°。当高阻旋转椭球体水平或直立时，视电阻率曲线关于中心对称且直立椭球体的极大值明显大于水平椭球体。视电阻率曲线的极大值约在异常体顶部附近，两侧有极小值点。倾向一侧的曲线较缓和而反倾向一侧的曲线较陡峭，随着倾角α的增大，视电阻率异常变大。

2.2 板状体的视电阻率曲线特征

板状体的视电阻率曲线与旋转椭球体的视电阻率曲线的走向大致相同。由于板状体的b轴趋近无穷大，因此板状体的视电阻率曲线相比旋转椭球体的曲线更缓和。

图6为低阻板状体的视电阻率曲线，模型参数为长度a=10,厚度c=2，中心埋深h=13。板状体分别沿顺时针旋转0°、30°、60°和90°。当低阻板水平或直立时，视电阻率曲线关于中心对称且水平板状体的极小值比直立板状体更小；当板状体倾斜时，异常体顶部附近的视电阻率异常为零，在倾向一侧有极小值，在反倾向一侧有极大值。随着倾角α的增大，视电阻率异常变弱。

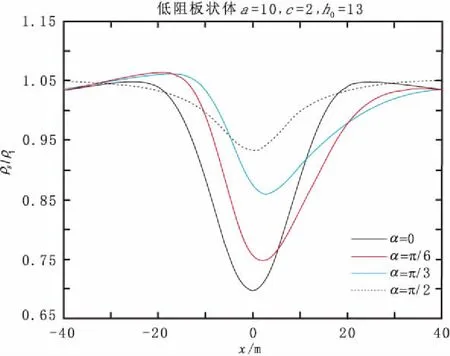
图6 低阻板状体的视电阻率曲线Fig．6 Apparent resistivity curve of plate with low resistance

图7为高阻板状体的视电阻率曲线，模型参数为长度a=10,厚度c=2，中心埋深h=13。板状体分别沿顺时针旋转0°、30°、60°和90°。当高阻板状体水平或直立时，视电阻率曲线关于中心对称且直立板状体的极大值明显大于水平板状体，视电阻率曲线的极大值约在板状体顶部附近，两侧有极小值点，倾向一侧的曲线较陡峭而反倾向一侧的曲线较缓和。随着倾角α的增大，视电阻率异常变大。

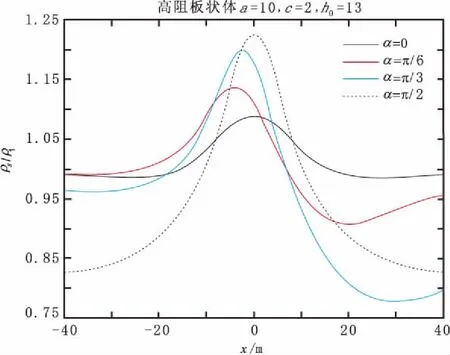
图7 高阻板状体的视电阻率曲线Fig．7 Apparent resistivity curve of plate with high resistance

3 结论

作者首先叙述了国内、外对椭球体的视电阻率异常的研究状况，在此基础上推导了均匀场中椭球体的电位和视电阻率的公式，得到了倾斜椭球体的视电阻率，并进一步简化得到板状体的视电阻率。对倾斜旋转椭球体和板状体的视电阻率曲线的变化规律进行了总结。

旋转椭球体与板状体的视电阻率曲线的走向大体相似。对于低阻情况，异常体顶部的视电阻率异常为零，在倾向一侧出现极小值，反倾向一侧有极大值，且倾角α越大，极大值越大，随着倾角α的增大，曲线逐渐变陡；对于高阻情况，视电阻率的极大值出现在异常体顶部，两侧有极小值，倾向一侧的曲线较缓和而反倾向一侧的曲线较陡峭，随着倾角α的增大，视电阻率异常变大。

参考文献：

[1] WEBB J H. The potential due to a buried spheroid[J]. Physical review,1931,38:2056-2067.

[2] 傅良魁,史元盛.论金属矿电阻率和形状对ρs异常值的作用规律[J].桂林冶金地质学院学报，1981(04)：1-12.

[3] 傅良魁,史元盛. 椭球体电阻率和形状对其视电阻率异常的影响[J]. 地球物理学报, 1982,25(04):382-386.

[4] 宋子齐. 椭球类矿体电场和磁场的一般性探讨[J]. 长安大学学报:地球科学版,1982(01):88-104.

[5] 雷林源. 论椭球位场函数的一般形式及其意义 [J]. 桂林工学院学报，1982(02):45-51.

[6] 张秋光.场论[M]. 北京：地质出版社,1985.

[7] 罗延钟，张桂青.频率域激电法原理[M]. 北京：地质出版社,1988.

[8] 强建科,何继善.椭球体上双频激电法的正演与反演算法[J].中南大学学报:自然科学版,2007,38(6):1199-1205.

[9] 徐淳宁,魏萍,刘阳.常用场源激励下椭球体电阻率的数值计算 [J].长春理工大学学报:自然科学版，2008,31(3):144-146.

[10] 段长生.椭球异常体中梯激电正反演研究[D].桂林：桂林理工大学,2010.

[11] 傅良魁. 电法勘探教程[M]. 北京：地质出版社,1980.

[12] 李金铭 .地电场与电法勘探[M].北京：地质出版社, 2005.

[13] 段长生,阮百尧,吕玉增,等.任意形态椭球体中梯激电异常计算[A]. 中国地球物理·2009[C]. 2009:263-264.

[14] 朱佩泓.均匀外电场中的介质球和椭球的场[J].宜春学院学报,2003,25(02):25-27.

[15] 中南矿冶学院.金属矿电法勘探[M].北京：冶金工业出版社,1980.

[16] 梁昆淼. 数学物理方法[M]. 北京：高等教育出版社,1998.