有限单元法求解水中二维体问题正演研究

林文东， 张志勇， 刘庆成， 汤洪志， 周 峰

(1.东华理工大学 核工程与地球物理学院，抚州 344000；2.中南大学 地球科学与信息物理学院，长沙 410083；3.东华理工大学 核资源与环境教育部重点实验室，南昌 330013)

0 引言

潜艇是现代海军的重要组成部分，近年来，潜艇的发展十分迅速，隐蔽性更强，使反潜变得越来越困难。早期以声响讯号探测水下的人造物体被应用的最为广泛，但随着减声降噪技术的发展，声纳技术遇到严峻挑战，且由于海洋环境的复杂，使灵敏度受到一定影响，同时声纳探测还有自身的诸如“声影区”的局限，非声探测技术将发挥重要的作用[1]。

磁异常探测技术是目前潜艇非声探测中得到应用最为广泛的，该技术具有分类能力好、定位精度高、执行时间短、成本低、不受浅海复杂环境影响等优点。但由于海洋背景磁场形成很强的磁场噪声，因此必须研究海洋背景磁场的特点和规律，以便从复杂的磁场信号中提取舰船或水下目标产生的磁场信号[2]。磁异常探测受自然条件影响较大，如雾、雨、雪、低云和风浪超过5级时，探测距离明显下降，虚警率也上升。当云层下缘低于100 m或水平视距小于1 000 m时，基本不能使用。同时随着潜艇消磁材料的发展，磁异常探测的效果也有所下降。

相对于传统潜艇探测技术，电磁法探测是近几年才开始起步的，夏立新译著的文章介绍了瞬变电磁法(TEM)探测掩埋水雷的可行性；孙东平等阐述了复杂电磁环境及其对潜艇隐蔽性的影响；傅金祝[3]给出了利用电磁法探测的初步研究成果。目前，国内相关研究大多数处于理论研究，实用性不足，并且缺少物理模型实验性的技术研究工作，极大地束缚了反潜装备的研发。

天然电磁场是由太阳微粒辐射(太阳风)作用下形成的地球磁层和电离层的变化，在地球表面有限区域内可视为平面波，其传播深度主要依赖于振动频率或者场的变化，大地电磁测深是通过对地面电磁场的观测，来研究地下岩矿石电阻率的分布规律的一种物探方法，其理论的关键是研究地面电磁场与地下岩矿石的电阻率存在的关系，电磁测深法广泛应用于地球内部结构、深部地质研究、深部找矿等领域，作者将电磁法探测应用到海洋中，同时引入有限单元法来研究水中二维体在天然电磁场中的异常场，以达到探测目的。有限单元的计算包括四个主要环节：①建立与所研究问题相符的数学物理方程与边界条件；②对计算模型进行离散化处理；③依据边值问题所满足的泛函，通过选择离散单元上的插值函数，形成钢度矩阵；④对稀疏线性系统进行求解，得到边值问题的解。相对于只考虑电阻率的情况，作者在此基础上加入了磁导率的概念，效果优于只考虑电阻率的情况。

图1 全球电场、磁场强度平均振幅谱特征图(Compbell,1967)Fig．1 Typical average amplitude spectrum of geomagnetic variations (Compbell,1967)

对于水下二维体的电磁法探测，有限单元的离散单元采用三角形剖分，三角单元可以更好地拟合复杂地形与地质单元。为了提高拟合效果，Key[4]等采用非结构化的自适应剖分算法进行海洋大地电磁的正演；Li[5]等利用非结构化网格进行了各向异性问题的二维大地电磁正演。非结构化网格剖分算法，有利于对地质单元与地形的拟合，且最大可能地保证剖分单元的质量、减少扩展区域单元数量。通过模型试算验证了二维大地电磁有限元算法在水下二维体探测中具有较高的精度和适用性，可以为电磁法探测水下潜艇打下坚实的基础。

1 天然电磁场下水中二维体的有限单元数值模拟基本原理

图1为全球电场、磁场强度平均振幅谱特征图，是1967年Compbell的研究成果，从图1可以看出，大地电磁测深法所观测的电磁场信号十分微弱，电场振幅最低仅为0.01 mV/km，磁场的振幅最低为0.001 nT，因此要求观测仪器要有很高的精度，同时有效地识别、抑制干扰噪声也是至关重要的。

根据麦克斯韦方程，角频率为ω(时间因子为e-iωt)的定态电磁场方程是[6-7]

▽×E=iωμH

(1)

▽×H=(σ-iωε)E

(2)

其中μ是介质的磁导率；σ是电导率；ε是介电常数。

对于海中二维体，取走向为z轴，x轴与z轴垂直，y轴垂直向上，当平面电磁波以任何角度入射海面时，海水中的电磁波总以平面波形式，几乎垂直的向下传播，将式(1)与式(2)按分量展开，可得到两个独立方程组，命名为E型波和H型波，也称TE模式和TM模式[6]。

E型：

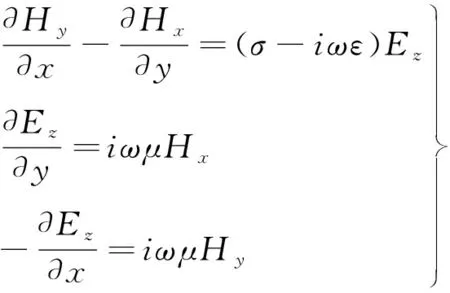
(3)

H型：

(4)

从式(3)和式(4)中的第二、三式中解出Hx、Hy和Ex、Ey，并分别带入第一式，得到偏微分方程[6-8]：

(σ-iωε)Ez=0

(5)

iωμHz=0

(6)

式(5)和式(6)可以统一表示成

▽·(τ▽u)+λu=0

(7)

(8)

u|Γ top= 1

(9)

δF(u)=0

(10)

其中 Ω为研究区域；Γtop为研究上边界，E型波取空气边界、H型波取海面边界；Γbottom为研究区域底边界。

根据有限单元剖分结果，泛函式(8)可表示为离散形式[6,9]

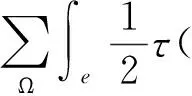
(11)

根据变分式子(10)，得到有限单元计算方程组

Ku=0

(12)

将边界条件式(3b)代入式(5)求解，即可得到节点的场值。

2 网格的三角剖分方法

鉴于各种地表的地球物理观测方法，一般都是浅部观测数据的分辨率高，到深部逐渐变差，基于这样的认识，在研究海中问题时，作者引入网格的三角剖分方法,剖分方法引自文章[10]。

图2 三角剖分Fig．2 Triangle split

3 水下二维体的电磁剖分单元钢度矩阵计算

网格剖分的最后单元为一次和二次插值三角形，利用一维、二维自然坐标[6]推导可得到单元上的钢度矩阵。三角单元节点逆时针编号i、j、m，若有二次插值节点则为i、j、m、r、p、q，其中r为边i,j为中点；p为边j,m中点、q为边m,i中点。下文中a、b、c的定义来自参考文献[6]。

3.1 泛函式(11)第一项单元积分

当选择双线性插值，K1e矩阵元素为

(13)

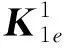
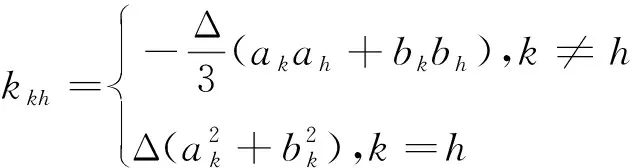
k,h∈{i,j,k}

(14)

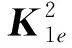
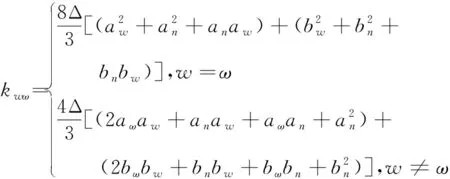
w,ω,n∈{i,j,k}&n≠w≠ω

(15)

(16)

3.2 泛函式(11)第二项单元积分

当选择双线性插值，则有

还原氧化石墨烯的形貌特征通过扫描电镜和透射电镜进行表征。图3是还原氧化石墨烯的扫描电镜图，(a)和(b)图是正面图，能够看到，经远红外光波制备的rGO表面是皱缩的，片层虽小但分布均匀。(c)和(d)图是截面图，能够发现，rGO呈絮状堆叠，片与片之间呈现较好的网状结构，这是静电喷雾以及远红外光波处理的结果，这种方法制备的石墨烯片层比较均匀，几乎是单层结构，这大大防止了石墨烯的团聚，而且得到的材料拥有更大的比表面积，对在超级电容器上的应用提供了理论支撑。

(17)

当选择双二次插值，则有

(18)

3.3 泛函式(11)第三项单元积分

当选择双线性插值，则有

(19)

当选择双二次插值，则有

(20)

4 算例分析

计算区域水平方向距离50 m，垂直方向取以2为底的对数,垂向空气剖分15层，海水剖分35层，模拟计算的空气、海水和水下二维体的电阻率、介电常数、磁导率如表1所示。计算其在TE、TM模式下的视电阻率。

表1 空气、海水和水下低阻体的电阻率、介电常数、磁导率

TE、TM计算结果如图3至图6所示。

图3 TM模式，只考虑电阻率的视电阻率(a)与视相位(b)断面图Fig．3 TM model, the section map of apparent resistivity (a) and apparent phase (b) when only consider the resistivity

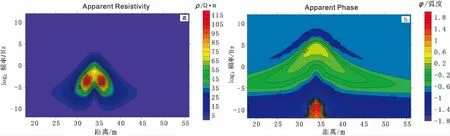
图4 TM模式，同时考虑电阻率与磁导率的视电阻率(a)与视相位(b)断面图Fig．4 TM model, the section map of apparent resistivity (a) and apparent phase(b) when consider the resistivity and magneticpermeability

图5 TE模式，只考虑电阻率的视电阻率(a)与视相位(b)断面图Fig．5 TE model, the section map of apparent resistivity (a) and apparent phase (b) when only consider the resistivity

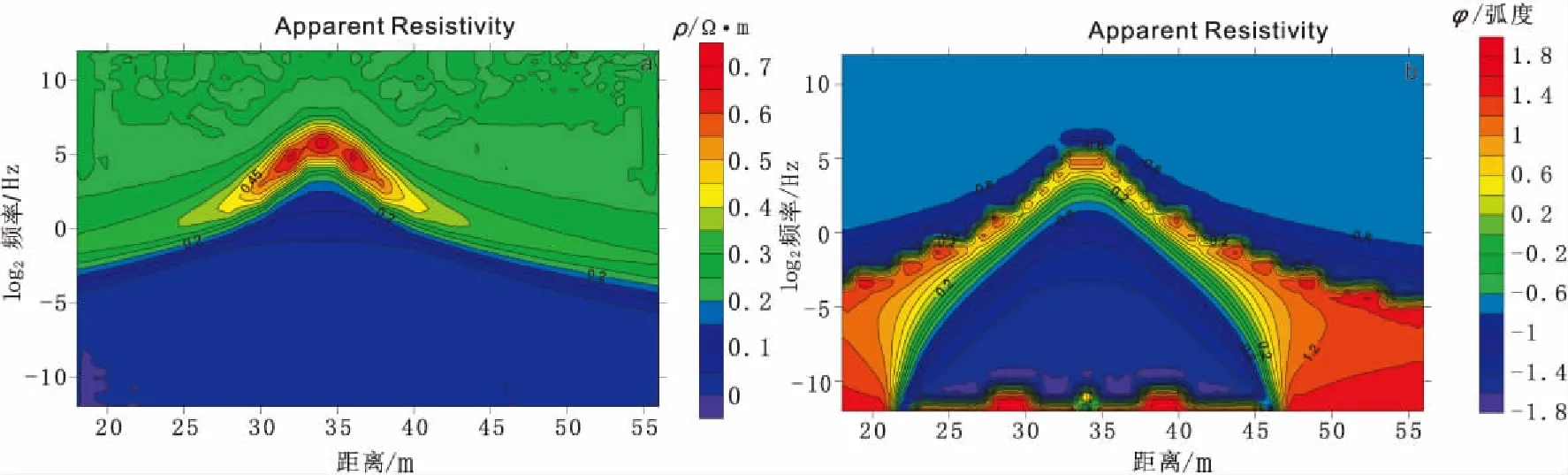
图6 TE模式，同时考虑电阻率与磁导率的视电阻率(a)与视相位(b)断面图Fig．6 TE model, the section map of apparent resistivity (a) and apparent phase (b) when consider the resistivity and magneticpermeability

图3与图4是在TM模式下的模拟计算结果，由计算结果可见，在只考虑电阻率的情况下，在上底30 m处左右形成低阻带状异常(图3)；同时考虑电阻率与磁导率，在相同位置处形成的异常曲线是封闭的，但异常值明显很大，可以很好地刻画出异常区域(图4)。TE模式的计算结果如图5、图6所示，图5中在上底30 m处左右形成高阻异常；在同时考虑电阻率与磁导率的图6中，在相同位置处形成的高阻异常值更大一些。

5 结论

作者研究了电磁法探测水中二维体的问题，基于大地电磁问题的有限单元正演，通过模型试算，验证了二维大地电磁有限元算法在水下二维体探测中具有较高的精度和适用性，得出如下结论：

(1)引入二维大地电磁有限单元正演来探测水下二维体,具有较高的精度和适用性。

(2)TM模式下，在低阻时，同时引入磁导率和电阻率的效果比只考虑电阻率探测异常效果要好；在引入磁导率的情况下，可以更好地圈定异常区域，从而确定水下二维体的位置。

(3)TE模式下，在低阻时，同时引入磁导率和电阻率的效果比只考虑电阻率得到的异常值要大，但是也可以刻画出存在异常的区域。

参考文献：

[1] 申会堂,张玉敏.海洋中的探测新技术[J].舰船科学技术,2001,1(3):61-64.

[2] 祝传刚,陈标,查玉龙，等. 基于海洋磁异常特征的目标定位理论和方法[J]. 青岛大学学报：自然科学版, 2008, 21(2):40-47.

[3] 傅金祝.探测掩埋水雷和临时爆炸装置的磁和电磁方法[J].水雷战与舰船防护,2011, 19(1):65-69.

[4] KEY K, WEISS C. Adaptive finite-element modeling using unstructured grids: The 2D magnetotelluric example[J].Geophysics, 2006,71(6): 291-299.

[5] LI Y, PEK J. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media[J].Geophys.J.Int., 2008,175: 942-954.

[6] 徐世浙.地球物理中的有限单元法[M].北京:科学出版社, 1994.

[7] MOHAMMAD I H,SRIGUTOMO W,SUTARNO D.The modeling of 2D controlled source audio magnetotelluric(CSAMT) responses using finite element method[J].Journal of Electromagnetic Analysis and Applications,2012(4):293-304.

[8] TONG X,LIU J,XIE W.Three-dimensional forward modeling for magnetotelluric sounding by finite element method[J].J.Cent.South Ualv.Technol,2009,16:136-142.

[9] 石宇，罗天涯，熊彬，等.有限元法求解各向异性介质中大地电磁场边值问题研究[J].地球科学前沿,2012(2):246-251.

[10] 张志勇，刘庆成.基于收缩二叉树结构网格剖分的大地电磁二维有限单元法正演研究[J].石油地球物理勘探,2013,48(3):482-487.