井地-高密度电法联合数值模拟研究

侯智超， 戴前伟， 尹俊涛,3

(1. 河南省交通规划勘察设计研究院有限责任公司， 郑州 450052;2.中南大学有色金属成矿预测教育部重点实验室， 长沙 410083; 3.中南大学 地球科学与信息物理学院， 长沙 410083)

0 引言

井地电法是通过在井中供入大功率的电流作为激发源，在地表布置一定数量的电极进行接收的勘探方式，是以地下介质的电阻率、极化率等差异为物理基础。井地电法在1958年由前苏联人[1]率先提出，并且首次用于圈定煤层水平边界；Alfano[2]计算了当在地下供电时，三层介质模型的地表电位解析解的分布，与常规电测深方法相比有更好的优势；Daniels[3]研究了球体和n层层状介质视电阻率的异常响应，其结果表明在井-井，井-地不同装置下并不存在“最好”的方法，其方法的选择取决于目标体的埋深、井井之间的间距等；在国内谭河清等[4]利用井地电位技术在孤东八区进行了剩余油分布的研究，其结果表明井地电位测量技术与其他监测的结果吻合很好，显示了井地电法技术在剩余油分布等方面良好的应用前景；王志刚等[5]进行了室内水槽的三维物理模型实验，研究物理场的分布特征和能有效圈定油藏边界和不同储层分布范围的最佳供电激发点的选择依据；屈有恒等[6]推导了倾斜线状电流源的理论电位，并且利用有限差分法计算了在垂直和倾斜线源情况下地表视电阻率分布的变化；汤井田等[7]根据井地有限元数值模拟的计算结果，提出了采用井地电阻率法歧离率确定高阻油气藏边界，讨论了不同深度油气藏和油气藏偏离钻井位置时歧离率的变化规律，结果表明歧离率可以很好地确定油气藏的异常并且对其横向边界圈定有很好的效果；戴前伟等[8]基于有限单元法对垂直线源井地电位法中的地下动态导体进行了三维数值模拟，其结果表明垂直线源井地电位对探测地下动态导体可行有效的；陈德鹏[9]利用有限元实现了任意线源井地电法三维正演模拟并分析了其异常规律；潘纪顺等[10]提出地面/井地/井间超高密度泛装置，为电阻率成像新方法的应用提供了新的思路和前景；高密度电法以直流电阻率法为基础，通过向地下发送电流形成稳定的电流场，在地表上布置多个电极进行电位测量，然后通过转换装置对布设电极的断面进行自动探测和记录的方法[11]；在进行野外测量时，井地电法一般是将源放于井中[12]，地表观测，使其有更大的探测深度，但是对于其横向的分辨率不够精确，因此作者采取井地电法和高密度电法进行联合正演模拟，将高密度电法和井地电法联合起来对地下目标体进行探测，能够使我们得到更多的地下场的信息，有助于在生产中实际问题的解决，具有很好的生产实践意义。

1 井地-高密度电法观测方式

井地-高密度电法的测量分为两种：①将供电电极放入井下慢慢移动，在地表利用测量电极测量地表电位分布情况，然后利用地表电位求取视电阻率(A为供电电极，M为测量电极，如图1所示)；②将电流源放在地表，其原理与高密度电法的测量方式相同(A为供电电极，M为测量电极 ，如图2所示)。

图1 井地电法测量方式示意图Fig．1 The borehole-ground electrical method measurement diagram

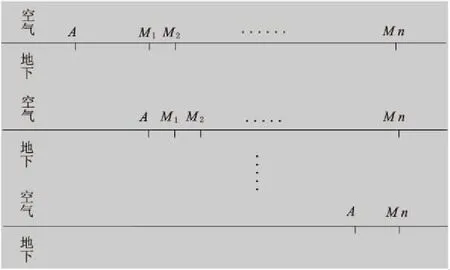
图2 高密度电法测量方式示意图Fig．2 The high-density resistivity method measurement diagram

两种测量方式主要是因为源位置的不同，而它们的测量电极都是在地表进行电位测量，因此在实际生产实践中可以将两种测量方式合二为一，通过源在地表和井中移动，分别采集数据。我们将采集的数据分别进行处理，当源在地表时，可以将采集的数据按照高密度电法数据进行处理；而当源在井中时，将其采集的数据作为井地电法数据进行处理。

2 2.5维井地-高密度电法的变分问题

井地电法和高密度电法都是点源的变分问题，其不同之处仅为点源的位置和最后记录点的选取，所以利用徐世浙[13]所述的方法，点源三维变分问题对z方向进行傅里叶变换可得2.5维边值问题

(1)

式(1)与下列变分问题等价

(2)

其中U是傅式变换的总电位；k为波数；σ为介质的电导率；I为电流；Γs是地面边界；Γ∞是无穷远边界;Ω为Γs和Γ∞组成的封闭区域；n为电流密度的法线方向；r是通过坐标原点、与走向垂直的截面内，Γ∞边界上的点至坐标远点的距离；K0是第二类零阶修正贝塞尔函数；K1是第二类一阶修正贝塞尔函数；cos(r,n)是矢径r与外法线方向n的夹角余弦。

3 有限单元法

有限单元法的求解步骤：

(1)网格剖分。首先将求解的二维区域剖分成矩形单元，如图1所示

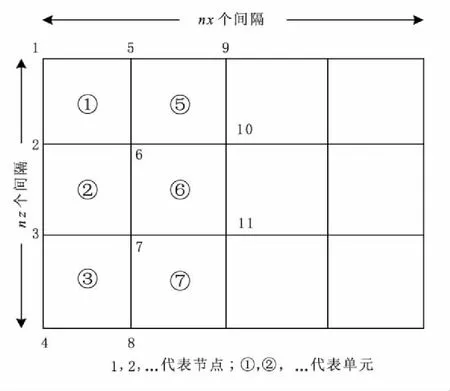
图3 网格剖分及节点编号示意图Fig．3 Sketch map of mesh division and node number

(2)线性插值。图4(a)是母单元示意图，图4(b)是子单元示意图，两个单元间的坐标变换关系为：

x=x0+(a/2)·ξ，z=z0+(b/2)·η

(3)

其中x0、z0是子单元中点的坐标;a、b是子单元的两个边长，微分关系为：

dx=(a/2)·dξ，dz=(b/2)·dη，dxdy=(ab/4)·dξdη

(4)

单元形函数为双线性插值形函数，可写为

(5)

其中ξi、ηi是点i(i=1,2,3,4)的坐标，形函数的分量可写为

N1=(1-ξ)(1-η)/4

N2=(1+ξ)(1-η)/4

N3=(1+ξ)(1+η)/4

N4=(1-ξ)(1+η)/4

(6)

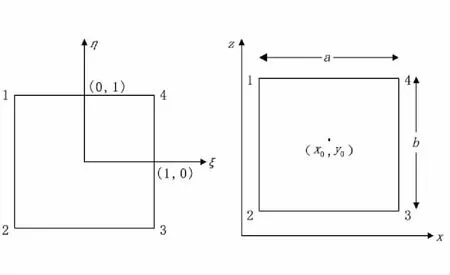
图4 母单元、子单元示意图Fig．4 Sketch map of parent element and sub-element(a)母单元；(b)子单元

(3) 单元分析及总体合成。式(2)中第一项积分为

(7)

其中K1e=(k1ij)；k1ij=k1ji；ue=(ui)T；i、,j=1、2、3、4。

式(2)中第二项积分为

(8)

式(2)中第四项积分为

(9)

根据δ函数的积分性质，式(2)中第三项积分为

(10)

式(10)说明只有点电源的UA对该项积分才有贡献。

将式(7)、式(8)、式(9)、式(10)带入到式(2)中得

(11)

将单元向量Ue扩展成ND×1的向量U，Ke扩展成ND×ND的矩阵K得：

KU=P

(12)

其中Ke=K1e+K2e+K3e；

(4) 方程组求解和视电阻率的计算。利用LDLT法求解线性方程组式(12)可得各节点傅氏电位U，然后通过反傅氏变换即可得到三维空间中的电位u。作者采用井地电法和高密度电法均为二极装置[15]进行观测，其视电阻率ρS计算公式为

(13)

其中K为装置系数；Δu为电位差。

4 模型算例及分析

在上述理论的基础上，编制了相应的程序，为了验证程序的正确性和有效性，首先对一地下均匀半空间模型进行正演模拟计算，并与解析解进行了对比分析，然后对一系列的模型进行了正演模拟计算。

4.1 模型1 地下均匀半空间模型

为了验证正演算法的可行性，作者选取均匀半空间进行计算。地下介质的电阻率为100 Ω·m，电流大小为1 A，计算区域为100 m×70 m，采用双线性插值，网格剖分为176×40。利用高密度正演模拟程序求出各节点的电位u，然后通过将电位代入视电阻率公式，求出视电阻率与地下真实电阻率进行对比。

图5为高密度电法得到的地下视电阻率的二维断面图，将视电阻率与地下真实电阻率进行对比分析， 经过计算得出的视电阻率最大值为 99.79 Ω·m，最小值为95.59 Ω·m，而且最小值基本存在于边缘区域，其最小相差为0.21 Ω·m，其误差为0.21%，最大相差为4.41 Ω·m，其误差为4.41%，确定了正演算法的有效性。

图6为井地电法得到的视电阻率曲线图，将视电阻率与地下真实电阻率进行对比分析，经过计算得出的视电阻率最大值为99.91 Ω·m，最小值为99.01 Ω·m，而且最小值基本存在于点源点附近，其最小相差为0.09 Ω·m，其误差为0.09%，最大相差为0.99 Ω·m，其误差为0.99%，确定了正演算法的正确性。

4.2 模型2高阻异常体模型

模型2如图7所示为单个对称的高阻体示意图，背景介质的电阻率大小为100 Ω·m，高阻体电阻率为1000 Ω·m，其顶部埋深为4 m，长为16 m，宽为8 m，与井中心对称。计算区域的大小为100 m×40 m，点电流源的供电大小为1 A。

首先利用井地电法，对上述模型进行有限元正演模拟，得到图8井地电法正演模拟的视电阻率拟断面图和图9井地电法正演模拟的视电阻率曲线图。从图9中可以看出，在高阻体的上方，视电阻率曲线表现出相对高阻的异常响应特征，当随着点电流源的向下移动，视电阻率响应逐渐增大，且幅度逐渐增大；当达到高阻体的上表面时，即当点电源在h=-4 m，其响应视电阻率达到最大，其异常极大值为ρs=186.56 Ω·m，随着点电源继续向下移动，即点电源在高阻体内部时，其视电阻率曲线逐渐减小，但仍然呈现相对高阻的响应特性，当点电源向下移动至高阻体的下表面，即h=-12 m，其响应视电阻率达到最小，其异常极小值为ρs=68.01 Ω·m，之后随着点电源深度的继续增加，其响应视电阻率曲线逐渐增大，慢慢趋向于背景介质的电阻率。从图8中可以看出，高阻体的上下表面正好对应两个异常中心深度的的位置。从图9中还可以看到，在高阻体的上方，视电阻率曲线图的曲线中间有一个拐点，其原因为当点电源离地表较近时，其地表测量电位受点电源的影响，而随着点电源深度的增大，其影响很小。

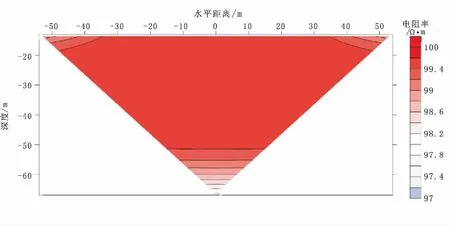
图5 均匀半空间高密度正演模拟断面图Fig．5 The forward modeling of high density resistivity section in the homogeneous half space

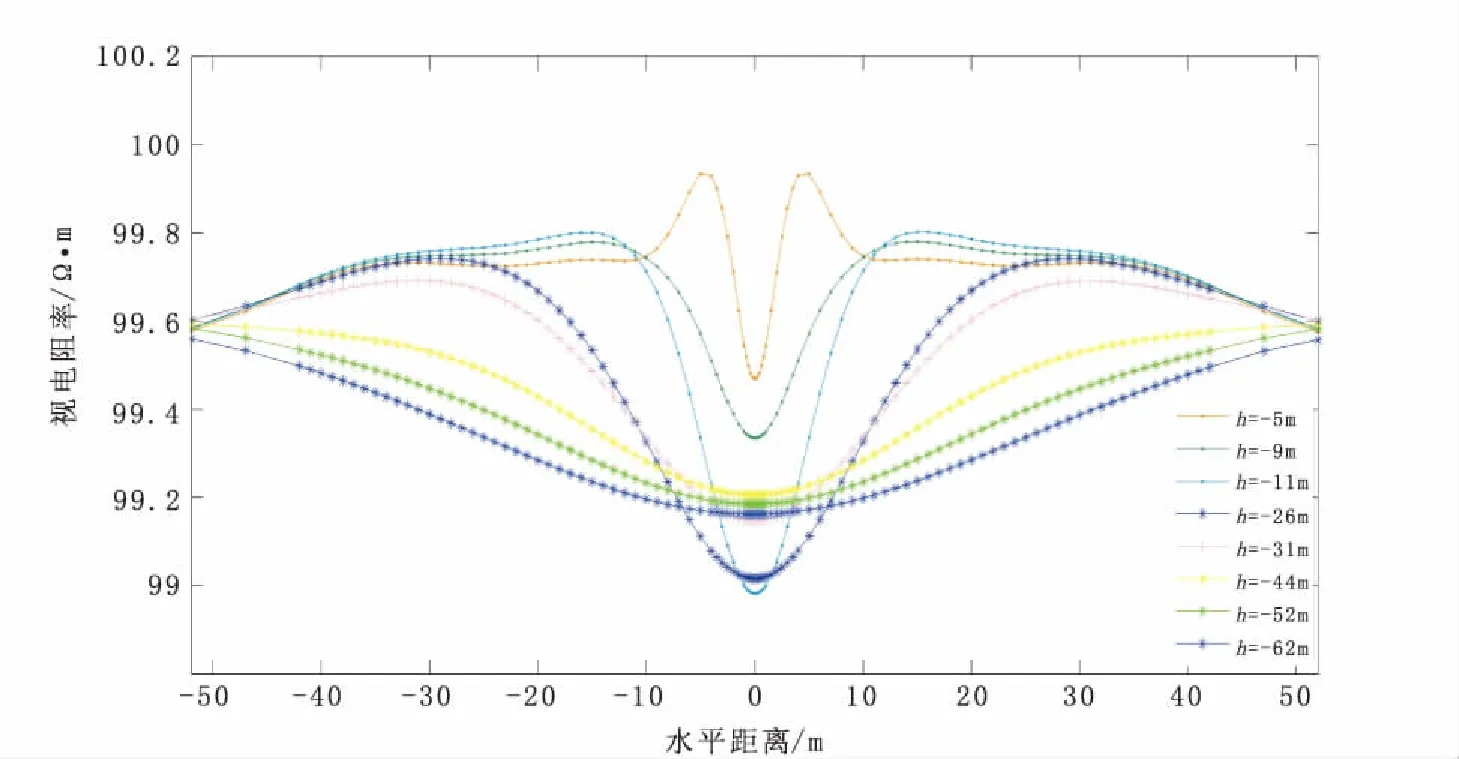
图6 均匀半空间井地电法正演模拟断面图Fig．6 The forward modeling of borehole-ground electrical section in the homogeneous half space

图7 高阻异常体示意图Fig．7 The high resistivity abnormality model

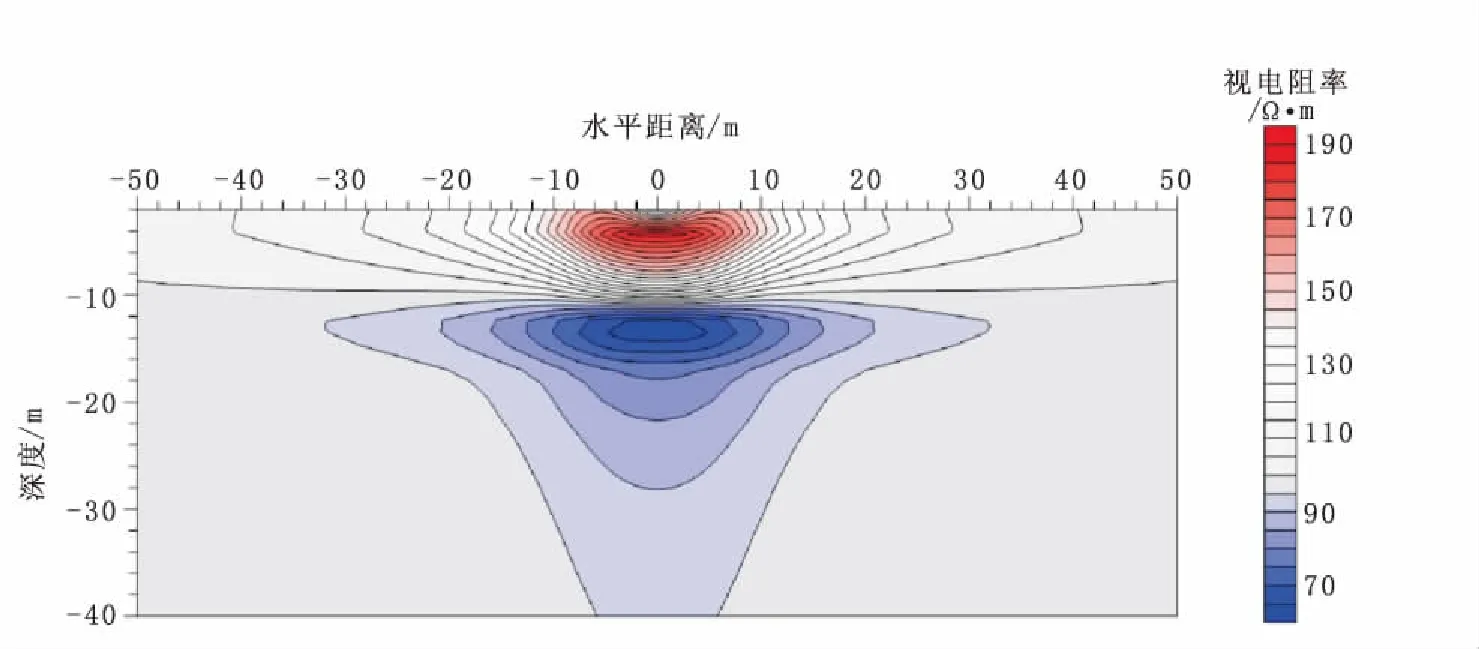
图8 模型2点电源不同深度视电阻率曲线分布图Fig．8 The curves of apparent resistivity with point current source in different depths of model 2

图9 模型2视电阻率拟断面图Fig．9 The apparent resistivity pseudosection map of model 2

图10为采用高密度电法对模型2计算得到的视电阻率断面图。从高密度电法正演模拟视电阻率断面图可以看出，在图10中出现了一个基本对称的相对高阻异常，其异常最大值为ρs=160.40Ω·m，在逐渐远离高阻体的位置，其响应视电阻率逐渐趋向于其背景介质的电阻率。在图10中可以看出，模型顶部埋深为-4 m，但是从高密度正演模拟的视电阻率断面图中可以看出，其纵向位置，异常的位置顶部约在z= -2 m处，在垂直方向上移了约2 m，这主要是受异常高阻体的体积效应的影响；而在横向可以看出，高阻异常闭合圈是关于x= 0 m对称的，其影响区域在x= -10m和x= 10m之间，与模型的位置一致。

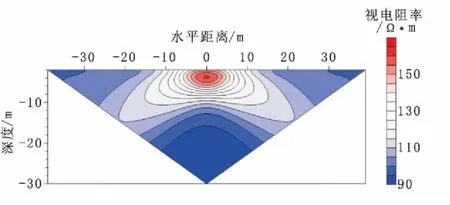
图10 模型2的高密度视电阻率断面图Fig．10 The high density apparent resistivity pseudosection map of model 2

从图8和图10中可以看出，井地电法和高密度电法均可以有效地对地下高阻异常体进行正演模拟。井地电法正演模拟中存在两个关于井对称的异常，上面是一个相对高阻异常，下面是一个相对低阻异常，而高阻体的上下表面正好对应两个异常中心深度的位置；高密度电法正演模拟中出现一个明显关于井对称的相对高阻异常，但是高阻异常的纵向位置有一定的偏差。

4.3 模型3边缘隐伏矿为高阻

图11为边缘高阻的模型示意图，背景介质的电阻率为100 Ω·m，高阻体的电阻率大小为 1000 Ω·m，高阻体顶部埋深为11 m，其长为10 m，宽为10 m，距井左侧10 m，计算区域大小约为100 m×50 m，点电流源供电大小为1A。

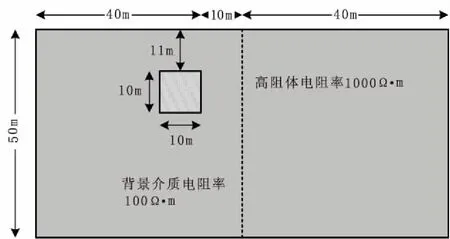
图11 边缘高阻的模型示意图Fig．11 The edge high resistivity abnormality model

图12为井地电法正演模拟的边缘高阻的拟断面图，从图12中可以看出，在距井左侧10 m左右有一个高阻闭合圈，而且闭合圈的中心在x= -15 m且z= -10 m的地方,而且在高阻闭合圈的下方，可以看出有一个类似低阻异常的闭合圈，低阻异常中心在x= -30 m且z= -22 m地方。这个从侧面说明，利用井地电法模拟时，在相对高阻异常下面会出现一个相对低阻异常的正确性。依照前面的异常规律响应，两个异常中心的z方向近似对应异常体的上下表面，从图12中也可以得到近似的响应，但是这时候并不能确定其异常体具体范围。因此需要结合源在地面时高密度正演模拟得到的图进一步确定异常体的范围。

图13为采用高密度电法对模型3计算得到的视电阻率断面图，从上图13可以看出，在距离井左侧10 m的位置，可以看出有一个高阻异常闭合圈，在纵向上从图13中可以看出，高阻异常闭合圈的顶部是在z= -5 m左右，而高阻模型顶部埋深在z= -10 m，其高阻异常在垂向方向上移了约5 m左右；在横向可以看出，这个高阻异常闭合圈是关于x= -15 m左右对称的，其影响区域约在x= -10 m和x= -20 m之间，这与模型的横向位置是一致的。

从图12和图13得出：通过井地电法可以圈定边缘高阻体的纵向上下表面的深度位置在z= -10 m到z= -22 m，从高密度电法可以近似圈定高阻体横向的范围约在x= -10 m和x= -20 m之间且关于x= -15 m对称，因此结合两种方法，可以近似确定边缘高阻异常体范围。

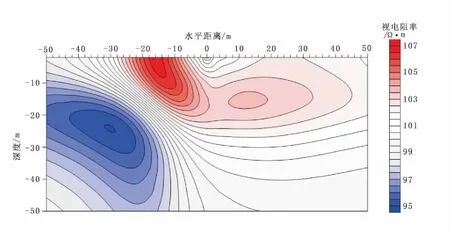
图12 模型3点电源不同深度视电阻率曲线分布图Fig．12 The curves of apparent resistivity with point current source in different depths of model 3

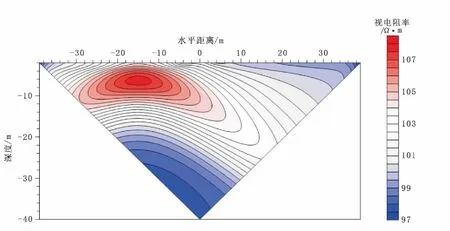
图13 模型3的高密度视电阻率断面图Fig．13 The high density apparent resistivity pseudosection map of model 3

5 结论

作者采用有限元法实现了井地-高密度2.5维视电阻率的正演模拟，给出了井地-高密度电法2.5维有限元正演模拟的详细解法；在井地电法正演模拟的基础上，对目标体进行高密度电法的正演计算，从而结合两者对目标体进行正演模拟，对地下目标体的范围可以更好地确定。

参考文献：

[1] 黄仲良.石油重·磁·电法勘探[M]. 东营:石油大学出版社,1999．

[2] ALFANO L. Geoelectric prospecting with underground electrodes[J]. Geophysics Prospecting,1961,10:290-303.

[3] DANIELS J J. Three-dimensional resistivity and induced polarization modeling using buried electrodes[J]. Geophysics,1977,42:1006-1019.

[4] 谭河清,沈金松,周超,等. 井地电位成像技术及其在孤东八区剩余油分布研究中的应用[J]. 石油大学学报：自然科学版, 2004,28(2):31-37.

[5] 王志刚,何展翔,魏文博,等. 井地电法三维物理模型试验[J]. 石油地球物理勘探, 2005,40(05):594-597.

[6] 屈有恒,张贵宾,晋风明. 倾斜线源的三维电场数值模拟研究[J]. 物探化探计算技术, 2007,29(5):431-435,370.

[7] 汤井田, 张继锋, 冯兵. 井地电阻率法歧离率确定高阻油气藏边界[J].地球物理学报, 2007, (03):926-931.

[8] 戴前伟,陈德鹏,熊健奎,等. 垂直线源井-地电位探测地下动态导体的三维有限元数值模拟[J]. 工程地球物理学报, 2008,5(6):643-647.

[9] 陈德鹏. 任意线源井地电法三维有限元正演研究[D]. 长沙:中南大学,2009.

[10] 潘纪顺,葛为中,折京平. 地面/井地/井间超高密度电阻率成像技术[J]. 华北水利水电学院报, 2010,31(2):74-78.

[11] 王鹏飞.超高密度激电数据采集与正反演解释方法研究[D]. 长沙:中南大学,2012.

[12] 李天成. 电阻率成像技术的二维三维正反演研究[D]. 北京: 中国地质大学, 2008.

[13] 徐世浙. 地球物理中的有限单元法[M]. 北京:科学出版社, 1994.