扩展的多约束最优制导律及其特性研究
温求遒,刘大卫,夏群利,李然
(1.北京理工大学宇航学院,北京 100081;2.中国兵器科学研究院,北京 100089)
扩展的多约束最优制导律及其特性研究
温求遒1,刘大卫2,夏群利1,李然1
(1.北京理工大学宇航学院,北京 100081;2.中国兵器科学研究院,北京 100089)
为满足侵彻攻击空地导弹末端制导要求,解决当前多约束制导律终端攻角控制问题,设计了包含受剩余飞行时间决定的控制量权函数,并引入到最优问题的目标函数中,基于线性二次最优控制理论推导得到一种扩展的多约束最优制导律。利用指令随时间变化解析表达式及伴随系数法,对制导律加速度指令变化规律及无量纲脱靶量特性进行了研究,证明了制导律指令的收敛性,从而为终端攻角控制创造了有利条件。同时,讨论了制导律增益n的设计原则。结合工程应用的需要,分别提出了一种制导初始条件设计方法及最大需用加速度的估计方法,可有效减小导弹末端机动。通过仿真验证了制导律及分析结论的有效性。
控制科学与技术;落角约束;最优制导律;加速度指令;终端加速度
0 引言
为了满足对地下坚固目标打击的需要,新一代空地制导武器广泛采用侵彻战斗部,要求制导控制系统不仅要达到一定的位置精度,且对终端入射角及攻角也提出了严格的约束[1]。传统的比例导引(PN)已无法满足制导任务的要求,需要发展多约束制导律。
终端角度约束制导律最初发展的典型代表为基于最优控制理论推导的最优制导律,其基本思想是将具有终端角度约束的制导问题转化为含终端约束条件的最优控制问题,后通过适当的假设和简化得到显式的制导方程[2-3]。其中Zarchan采用Schwartz不等式推导了包含落角约束的最优制导律,并基于小角度假设,进一步转换成弹道成型制导律(OGL/IAC)[3];Song等利用极大值原理推导出了以时间最短为性能指标的最优导引律[4-5]。
在最优制导律取得新进展的同时,一些学者还研究在经典比例导引律基础上增加偏置项的偏置比例导引律来实现角度控制。Kim等在导弹速度不变和目标无机动的假设下,研究了具有时变偏差项的偏置比例导引律[6]。根据弹目相对运动的数学规律,在线调整PN系数,是实现终端角度约束的另一种思路。Lu等在2005年针对高超声速飞行器发表了一种三维空间内考虑落角和入射方位角约束的制导律[7]。
变系数比例导引律、偏置比例导引律和其他类型制导律虽然在理论上能够满足角约束制导问题,但存在制导律结构复杂、制导信息种类和精度要求高等缺点,使得其工程实现困难,与之相比,具有终端多约束的最优制导律是目前研究最广泛且工程应用简便可靠的制导方法,但该类制导律在推导过程中并未考虑到侵彻攻击对终端攻角的约束,同时在纵向制导平面也未考虑重力的影响,因此并不能完全满足侵彻攻击空地导弹末端制导的要求。
为解决当前多约束制导律终端攻角控制问题,本文首先以剩余飞行时间倒数的幂函数为控制量权系数,建立新型目标函数,并在状态方程建立时引入重力项,得到了一种扩展的多约束最优制导律(EOGL/IAC)。该制导律在实现落点及落角控制的同时,通过在末端加入指令积分权函数及调整重力补偿系数方式实现终端零加速度指令,为攻角控制创造了有利条件。在此基础上,进一步推导了制导律指令随时间无量纲表达形式,并证明了制导律指令的终端收敛性及最大需用加速度对应制导时刻。通过建立简易制导模型及相应伴随分析系统,分析了不同误差源及制导律增益对脱靶量及终端加速度的影响,给出了制导律各项脱靶量收敛条件。结合工程应用需求,给出了满足最小机动要求的制导初始条件与最大需用加速度估计算法。最后通过非线性仿真证明了分析结论的有效性。
1 最优制导律的推导
导弹制导问题的线性简化模型如图1所示。图中:am为导弹加速度,ac为导弹加速度指令,g为重力加速度,at为目标加速度。

图1 制导律推导用模型Fig.1 Model for derivation of guidance law
对于静止目标有at=0,则图1给出的模型可表示为如下状态方程的形式:
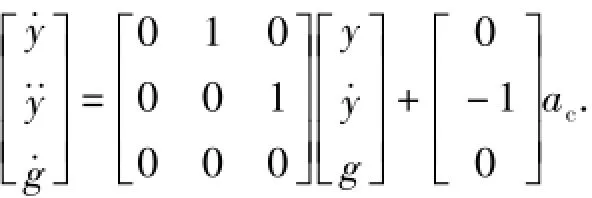


为保证终端位置和角度均达到期望约束,可将终端角度约束转化为法向速度约束,因此有期望的终端状态式中:tgo为剩余飞行时间,tgo=tf-t,在实际工程中可以通过弹目相对距离与导弹速度计算得到。
(2)式为以导弹的位置相关状态量、终端约束、重力加速度及剩余飞行时间表示的最优制导律,但这些信息无法全部由导引头等弹上硬件直接测量,从而限制了制导律的工程应用性,因此需对制导律进行进一步的转换。
假设视线角足够小,则视线角及角速度存在如下近似关系:


n取不同值并带入(4)式中,如表1所示给出的各项系数计算结果。
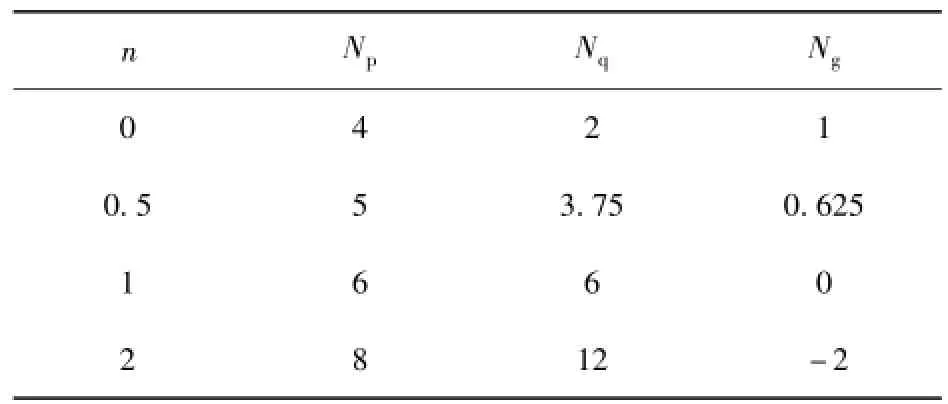
表1 不同n取值下对应制导律系数Tab.1 The coefficients of guidance law for different values n
不难发现,当n=0时,制导律等同于OGL/IAC[3];由于Np与n成一次关系,而Nq与n成二次关系,因此随着n的增加,落角项相对于PN项在制导指令中所占的比重不断增大,如图2所示。这将使导弹在制导初始段便以较大的加速度完成相对于期望落角方向的位置调整,同时也减小了终端需用加速度。
但是,较大的n值将使得制导权系数过大,降低了制导律对制导信号噪声的鲁棒性。由表1可见,当n>1时,Np>6,已超过通常PN系数2~6的取值范围[2]。
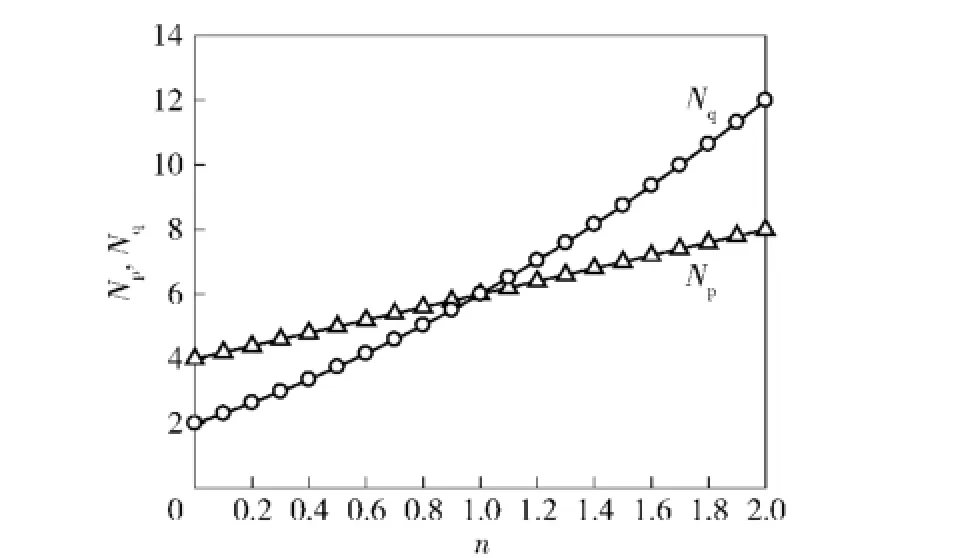
图2 Np及Nq随n变化曲线Fig.2 Npand Nqvs.n
2 多约束制导律特性分析
2.1 指令变化规律
通常,导弹在弹目视线坐标系下有初始位置y(0)=0,且在小角度假设下y·(0)=vrε0,y·(tf)= vrqf,将以上初值带入(2)式中,制导指令可表示为由初始速度方向偏差ε0、终端落角约束qf及重力g三部分产生的指令和


2.1.1 初始加速度指令

由(7)式不难发现,初始加速度与相对速度vr、落角约束qf及制导律增益n呈正比,而与制导时间tf呈反比。
2.1.2 终端加速度指令
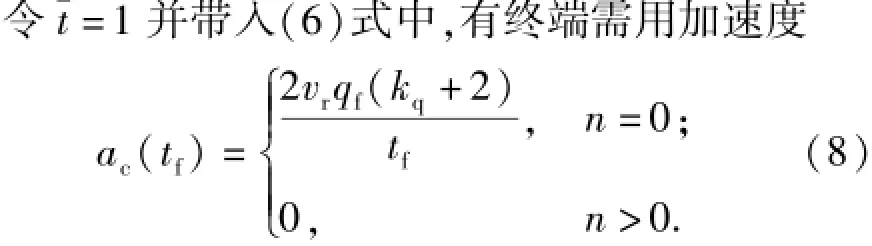
由(8)式可见,当n>0时,ac(tf)=0,制导律的末端指令总是收敛至 0;对OGL/IAC,对应n=0,显然仅当kq=-2,终端指令才会为0,但对于侵彻制导武器,通常要求落角qf<-50°,因此满足kq=-2的制导条件是很难构成的。
2.1.3 最大加速度指令
导弹的最大可用加速度是有限的,因此总是希望最大加速指令尽可能小。同时如果最大需用加速度出现在初始时刻,则在末端将允许导弹有更多的可用加速度用于消除各种外界干扰及制导信号误差,从而保证获得更好的精度。


表2 不同kq取值下ac(t)变化特性Tab.2 The change characteristics of ac(t)for different values kq

以上分析表明,只要取足够大的制导律增益,则制导律在制导初始时刻会出现最大需用加速度,并在制导终端收敛至0.
2.2 脱靶量变化规律
由于EOGL/IAC是包含终端位置和角度约束的最优制导律,因此必须分别对其位置脱靶量及角度脱靶量进行分析。
为了研究方便,将控制系统等效为一阶动力学滞后环节,如图3所示给出了考虑动力学滞后环节的EOGL/IAC制导回路工作原理框图。其中:Tg为导弹动力学时间常数;Δy(tf)为位置脱靶量;Δq(tf)为角脱靶量。
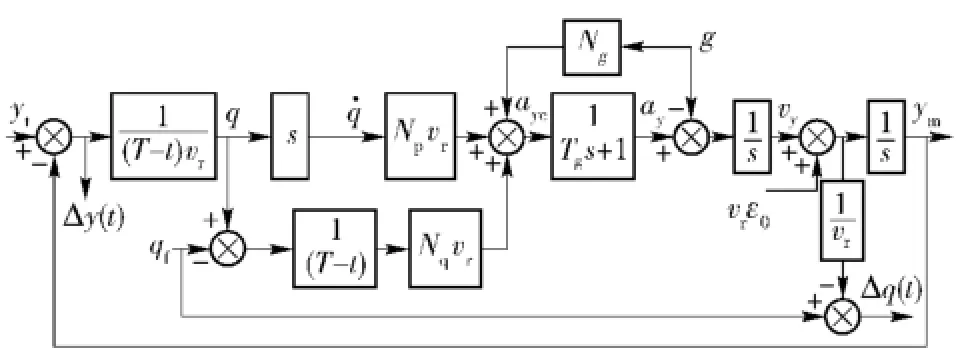
图3 制导律闭环原理框图Fig.3 The functional block diagram of closed loop of guidance law
取Tg=0.3 s,tf=15 s,ε0=5°,qf=-50°,对于不同制导律增益n,如图4所示给出了对应弹体加速度曲线。随着n值的增大,加速度在初始时刻值越大,而在终端的收敛速度越快。受到控制系统动力学滞后的影响,如图5所示,仅当n>0.5时才能保证终端加速度小于1个g.
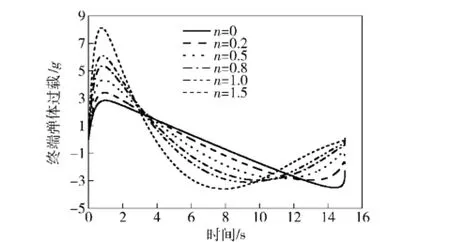
图4 不同n取值对应过载变化曲线Fig.4 The acceleration curves of missile for different values n
为比较在不同干扰下制导律脱靶量变化情况,分别取初始速度指向误差、终端落角约束、重力加速度干扰为系统主要误差源,基于伴随法的思想[3],图6和图7分别给出了无量纲位置脱靶量和角度脱靶量伴随系统工作原理框图,其中设无量纲参数t= t/Tg,=sTg.对应不同误差源,如图8和图9所示,分别给出了与之对应的无量纲位置脱靶量、

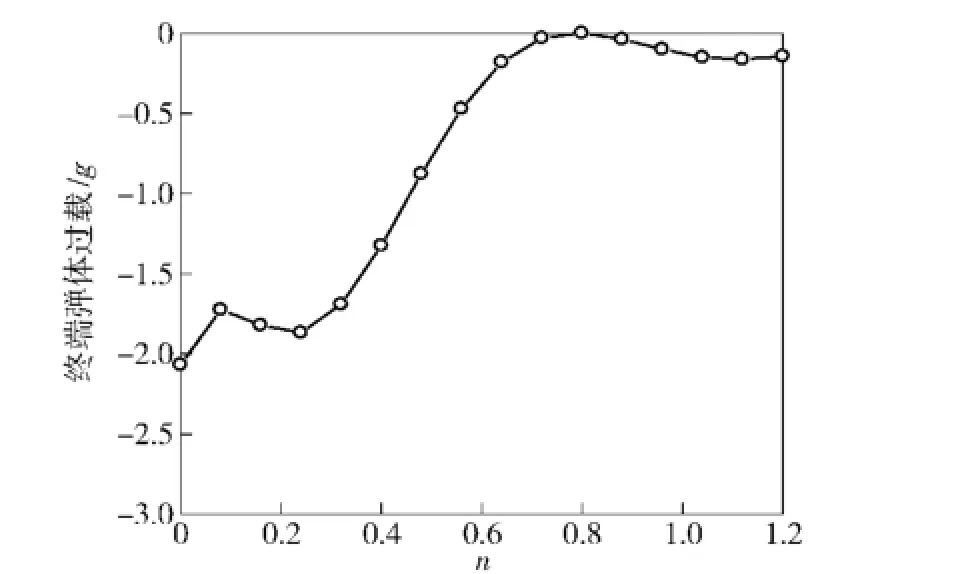
图5 不同n取值对应终端过载值Fig.5 The terminal accelerations for different values n
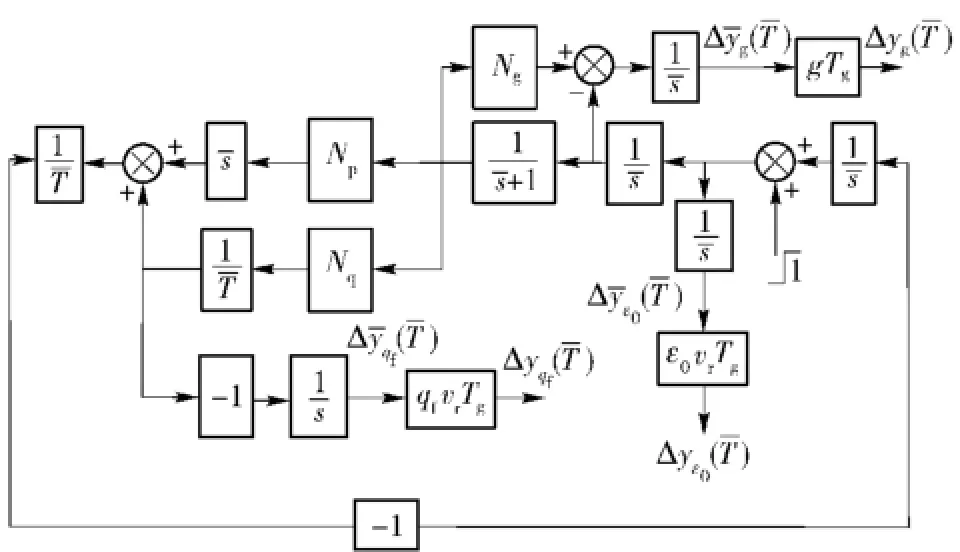
图6 位置脱靶量伴随系统Fig.6 Position miss distance adjoint system
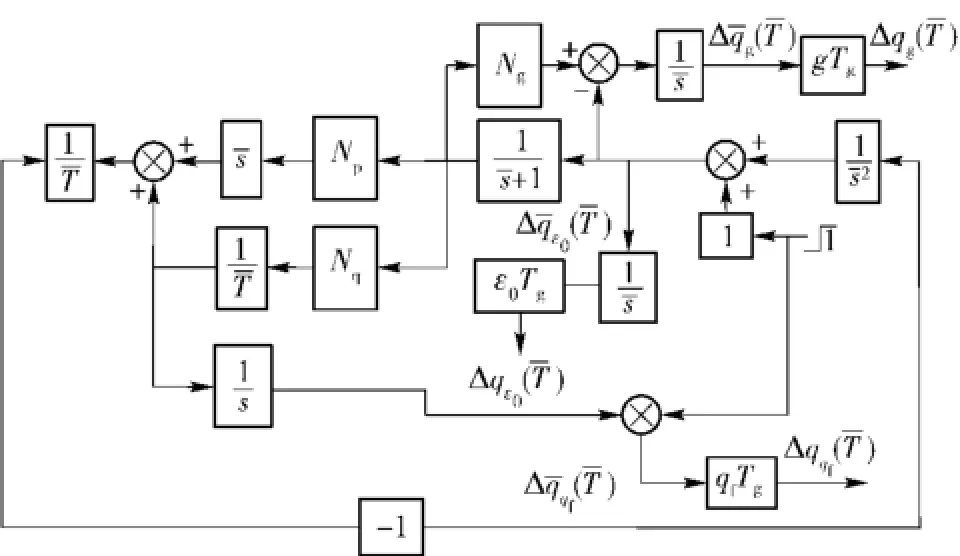
图7 角度脱靶量伴随系统Fig.7 Angle miss distance adjoint system
由图8和图9可见:
1)制导律无量纲位置脱靶量及角度脱靶量均随着无量纲末导时间增大而收敛,保证位置及角度脱靶量为0的条件分别是末制导时间至少为控制系统动力学时间常数的14倍和16倍。
2)相比于PN(收敛条件为10倍动力学时间[3]),EOGL/IAC在使用上对制导时间有更为严格的要求。
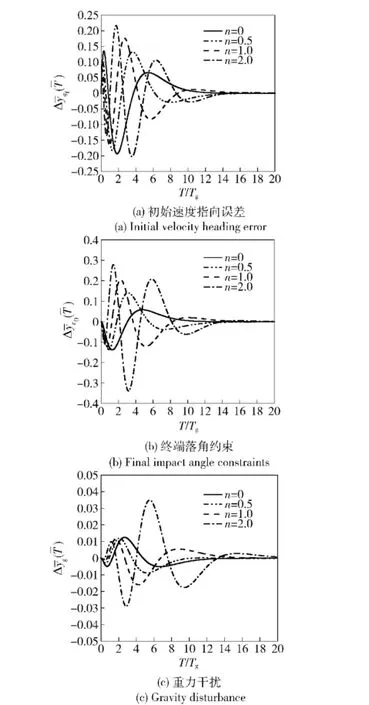
图8 不同T/Tg对应无量纲位置脱靶量曲线Fig.8 Dimensionless position miss distance curvesfor T/Tg
3)n取值越大,2项脱靶量的相对收敛越慢,且收敛过程中脱靶量值越大,这表明提高制导律增益后,制导律在制导时间不足时鲁棒性下降。
3 制导律工程应用
3.1 最优制导初始条件计算
对于导弹制导控制系统设计者来说,总是希望控制导弹以最小的机动命中目标并满足各种约束。因此,设计一个合理的初始条件、尽量降低导弹的机动加速度需求具有十分重要的意义。
首先引入函数E,并有

图9 不同T/Tg对应无量纲角度脱靶量曲线Fig.9 Dimensionless angle miss distance curves forT/Tg
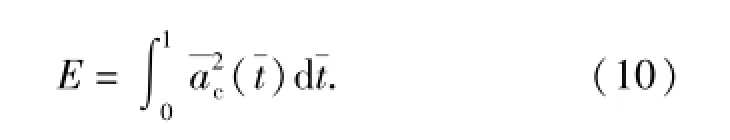
由(10)式可知,E表征了导弹在整个制导过程中消耗的能量。将(6)式带入(10)式中,有
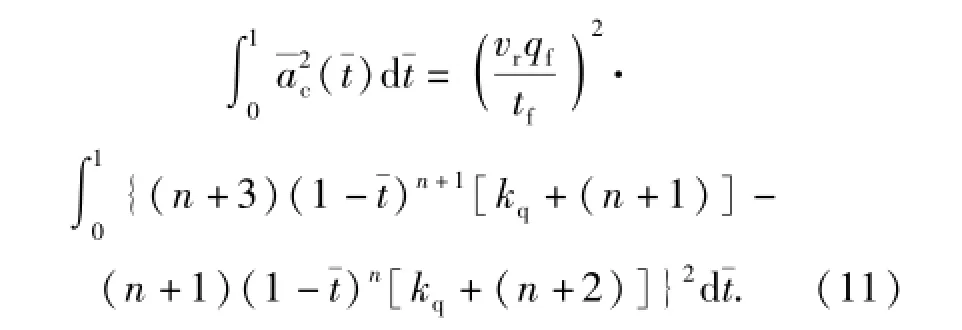

对于实际制导过程,如图10给出的弹目相对几何关系,有

式中:θ0为初始速度倾角;q*f为相对视线坐标系的落角约束值;qLOS_0为初始弹目视线角。
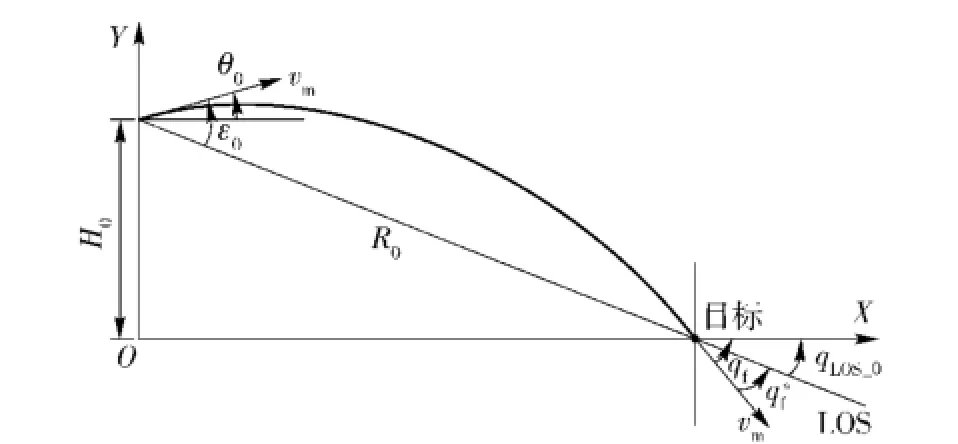
图10 弹目相对几何关系Fig.10 Intercept geometry
将(14)式带入(12)式中,并根据kq定义,可得
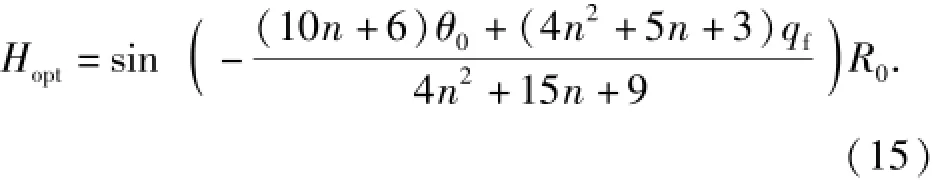
由(14)式,对于确定的末制导距离R0、导弹初始速度倾角θ0,即可确定转入制导的最优高度Hopt.
3.2 最大需用加速度估计
根据(12)式,对于不同的n值,基于最小机动条件,不难得到期望的kq值,通过对比由(9)式给出最大加速度判定区间,可知制导律的最大需用加速度必然出现在初始时刻。
考虑重力补偿项,则最大需用加速度可表示为
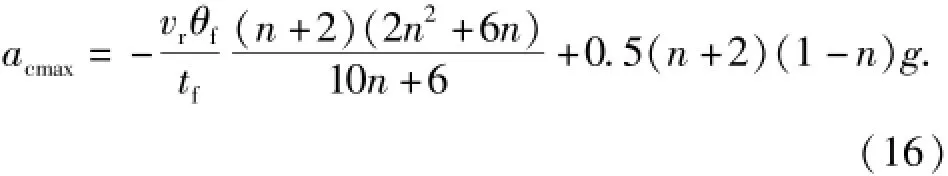
在给定气动特性和飞行状态下,在最大攻角限制条件下,导弹的最大可用加速度值不难得到。对比需用加速度与可用加速度值,即可快速判定当前制导律增益、制导条件选择是否合理,并进行调整。
4 仿真与验证
以某远程电视制导空地导弹为例[8],相关的制导初始条件及终端约束要求为:导弹飞行速度vm= 220 m/s,初始弹道倾角θ0=0°,初始弹道偏角ψv0= -2.5°,控制系统时间常数Tg=0.3 s,导引头作用距离Rs=4 km,终端落角约束qf=-70°.
由于导弹在中制导段采用定高巡航飞行,因此可以根据要求爬升至一定的高度转入末制导,待导引头捕获目标才转入末制导,从而为构造最优的初始条件创造了基础。因此仿真中,制导的初始弹目距离可确定为R0=Rs.
侧向制导采用标准的比例导引制导律。
由于导弹在进入末制导阶段采用定高平飞,对应θ0=0°,则不难预估制导时间tf≈R0/vm,结合其他制导输入参数,带入(14)式和(15)式中,可得制导初始高度及估计最大需用过载Hopt=1 902 m, acmax=1.45g.
为了便于对比,在初始弹目距离不变的前提下,将进入高度分别取为2 500 m、1 500 m.如图11和图12所示,给出了弹道仿真结果。可见,制导律可保证导弹命中目标并达到期望落角。且导弹加速度在末端能快速收敛并接近于0,为实现攻角约束创造了很好的条件。对比不同初始条件对应仿真结果可见,采用最优高度转入末制导的弹道变化最平滑,且制导过程消耗能量明显小于其他条件。对制导最大需用加速度的估计与对应实际仿真结果符合,从而证明了估计算法的准确性。

图11 纵向弹道曲线Fig.11 Vertical trajectory curves of missile
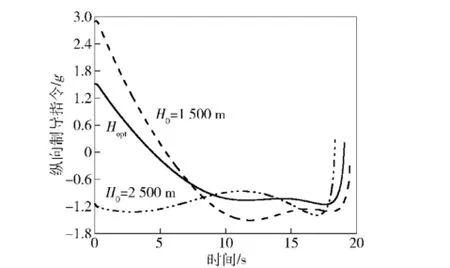
图12 导弹机动过载曲线Fig.12 Acceleration curves of missile
为进一步验证制导律的鲁棒性,采用白噪声的形式,引入两通道制导指令噪声及剩余飞行时间解算误差,并取方差σΔayc=σΔazc=0.15g,σΔtgo=0.5 s.
采用蒙特卡洛仿真,取仿真次数为500.如图13~图15所示,给出了对应落点、终端落角及弹体加速度散布情况。不难看出,制导律在存在制导信息噪声情况下依然很好地满足各项终端约束要求。
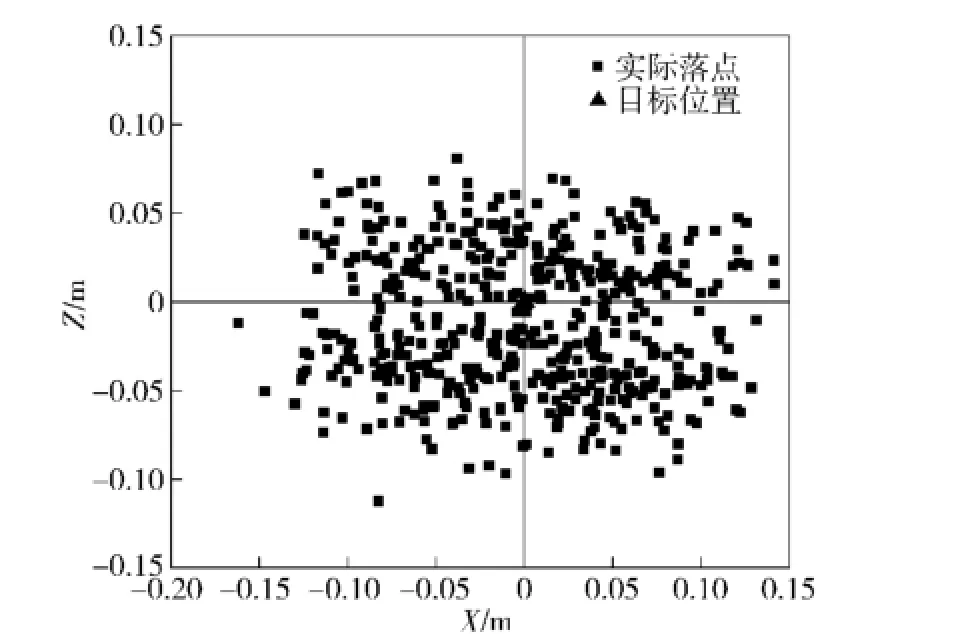
图13 落点散布曲线Fig.13 Dispersion of terminal impact points
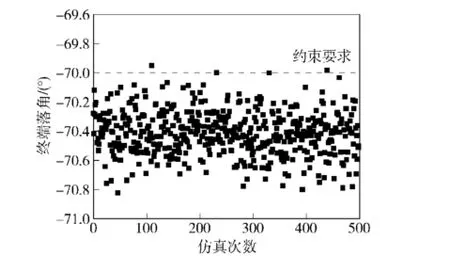
图14 终端落角散布曲线Fig.14 Dispersion of terminal impact angles

图15 终端弹体加速度散布曲线Fig.15 Terminal acceleration of missile dispersion
5 结论
针对导弹终端位置与落角约束制导问题,推导得到一种扩展的多约束最优制导律,研究了制导律指令变化规律及无量纲脱靶量特性,给出了制导律增益n的设计原则。通过理论分析与数学仿真,得出如下结论:
1)扩展的大落角制导律能同时满足终端位置及角度约束条件,当n>0时,制导律终端加速度指令能收敛至0,有利于末端小攻角约束的实现。同时对多数制导条件,制导律的最大需用加速度出现在初始时刻,有利于提高命中精度。
2)制导律位置及角度脱靶量均收敛至0的条件是末制导时间至少应大于16倍控制回路动力学时间常数,因此大落角制导律使用的条件需保证足够的末制导距离。
3)系数n的取值对制导律性能影响较大,当n取值偏小时,加速度指令末端收敛速度变慢;而n取值偏大时,制导律对各种干扰的鲁棒性下降,位置及角度脱靶量增大,因此建议n取值在0.5~1.0之间。
4)在已知末制导距离、期望落角及初始速度倾角条件下,给出了使导弹制导过程中机动最小制导初始条件计算方法及最大需用加速度估计策略,对制导律的工程化应用具有重要的意义。
References)
[1] 蔡洪,胡正东,曹渊.具有终端角度约束的导引律综述[J].宇航学报,2010,31(2):315-323.
CAI Hong,HU Zheng-dong,CAO Yuan.A survey of guidance law with terminal impacts angle constraints[J].Journal of Astronautics,2010,31(2):315-323.(in Chinese)
[2] 刘大卫,夏群利,崔莹莹,等.具有终端位置和角度约束的广义弹道成型制导律[J].北京理工大学学报,2011,31(12): 1408-1413.
LIU Da-wei,XIA Qun-li,CUI Ying-ying,et al.Generalized trajectory shaping guidance law with both impact position and angle constrains[J].Transactions of Beijing Institute of Technology,2011, 31(12):1408-1413.(in Chinese)
[3] Zarchan P.Tactical and strategic missile guidance[M].Reston: American Institute of Aeronautics and Astronautics,1997.
[4] Song T L,Shin S J,Cho H.Impact angle control for planar engagements[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(4):1439-1444.
[5] Song T L,Shin S J.Time-optimal impact angle control for vertical plane engagements[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(2):738-742.
[6] Kim B S,Lee J G,Han H S.Biased PNG law for impact with angular constrain[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
[7] Lu P,Doman D B,Schierman J D.Adaptive terminal guidance for hypervelocity impact in specified direction[J].Journal of Guidance,Control,and Dynamics,2006,29(2):269-278.
[8] 温求遒,夏群利,祁载康.图像制导空地导弹攻顶弹道方案研究[J].弹箭与制导学报,2010,30(3):8-10.
WEN Qiu-qiu,XIA Qun-li,QI Zai-kang.Research of trajectory scheme with large impact angle for imaging guided AGM[J].Journal of Projectiles,Rockets,Missile and Guidance,2010,30(3): 8-10.(in Chinese)
Research on an Extended Optimal Guidance Law with Multiple Constraints
WEN Qiu-qiu1,LIU Da-wei2,XIA Qun-li1,LI Ran1
(1.School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China;
2.Ordnance Science and Research Academy of China,Beijing 100089,China)
An extended optimal guidance law with terminal miss distance and impact angle constrains is derived.The guidance law is obtained as the solution of a linear quadratic optimal control problem with the goal function weighted by a power of the time-to-go.Based on the analytical expression for the change of guidance command with time and the adjoint system analysis method,the command characteristics and dimensionless miss distance of guidance law are analyzed.The result shows that the acceleration command of guidance law can be converged into zero in the final time of guidance,which may create a good situation for terminal angle of attack control.A design principle for selection of guidance law gain is discussed.Finally,according to the requirements of engineering application,the methods on calculating the guidance initial condition and maximal required acceleration are given.The effectiveness and practicality of the guidance law are demonstrated through simulation.
control science and technology;impact angle constraint;optimal guidance law;acceleration command;terminal acceleration
V488.133
:A
1000-1093(2014)05-0662-08
10.3969/j.issn.1000-1093.2014.05.013
2013-08-06
中国博士后科学基金一等项目(2008M00006);中国博士后科学基金特别项目(2012T50048)
温求遒(1982—),男,讲师,博士后。E-mail:wenqiuqiu82@gmail.com;
夏群利(1971—),男,副教授。E-mail:1010@bit.edu.cn

