冲击载荷作用下中间轴承流体润滑性能研究

(中国舰船研究设计中心，武汉 430064)

中间轴承是舰船轴系的重要附属设备，其工作性能的好坏将直接影响到舰船推进轴系的性能。在船舶航行过程中，随着外来载荷的变化，轴系的运行性能会受到较大影响，尤其当船体受到外来冲击爆炸时，常常会干扰各轴承的正常润滑性能，从而影响轴系的正常运转[1]。本文通过建立中间轴承的润滑模型，以冲击载荷为输入条件，定性的分析了中间轴承在冲击载荷作用下各参数的变化情况，提出一种润滑性能计算方法。

1 中间轴承理论建模

1.1 对轴承建立坐标系

图1a)中O1、O2分别为轴承与轴颈的圆心。为便于描述轴颈表面各点油膜厚度，建立圆柱坐标系x-y，将油膜沿圆周方向展开成矩形，见图1b)。x轴为圆周方向，起点与θ=0相对应；y轴为轴承轴线方向，起点为轴承一端面。

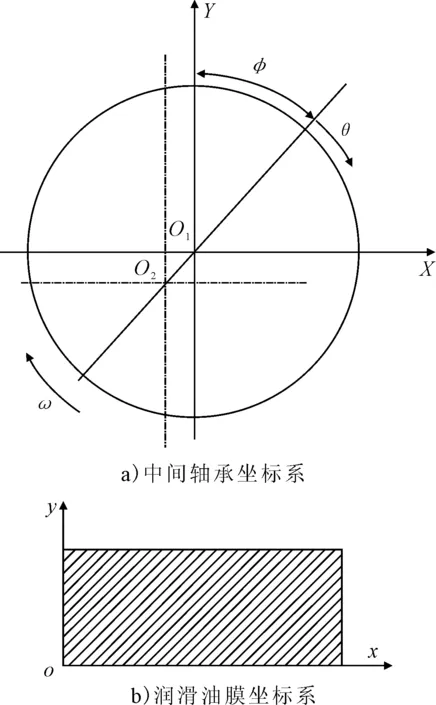
图1 流体润滑分析坐标系示意

1.2 基本控制方程

流体润滑研究所采用的基本控制方程为Reynolds方程，在该模型中考虑了润滑表面粗糙度的影响作用，基本控制方程如下[2]。

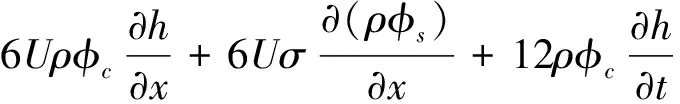
(1)

式中：h——油膜厚度；

p——油膜压力；

x——轴承圆周方向坐标；

y——轴承轴向坐标；

U——轴颈外表面与轴承内表面相对运动速度；

μ,ρ——润滑油粘度及密度；

t——时间项；

φx，φy——润滑表面沿x、y方向上的压力流量因子；

φs——剪切流量因子；

φc——量纲一的量因子，即接触因子。

1.3 油膜厚度的求解

中间轴承油膜厚度h的变化规律见图2。

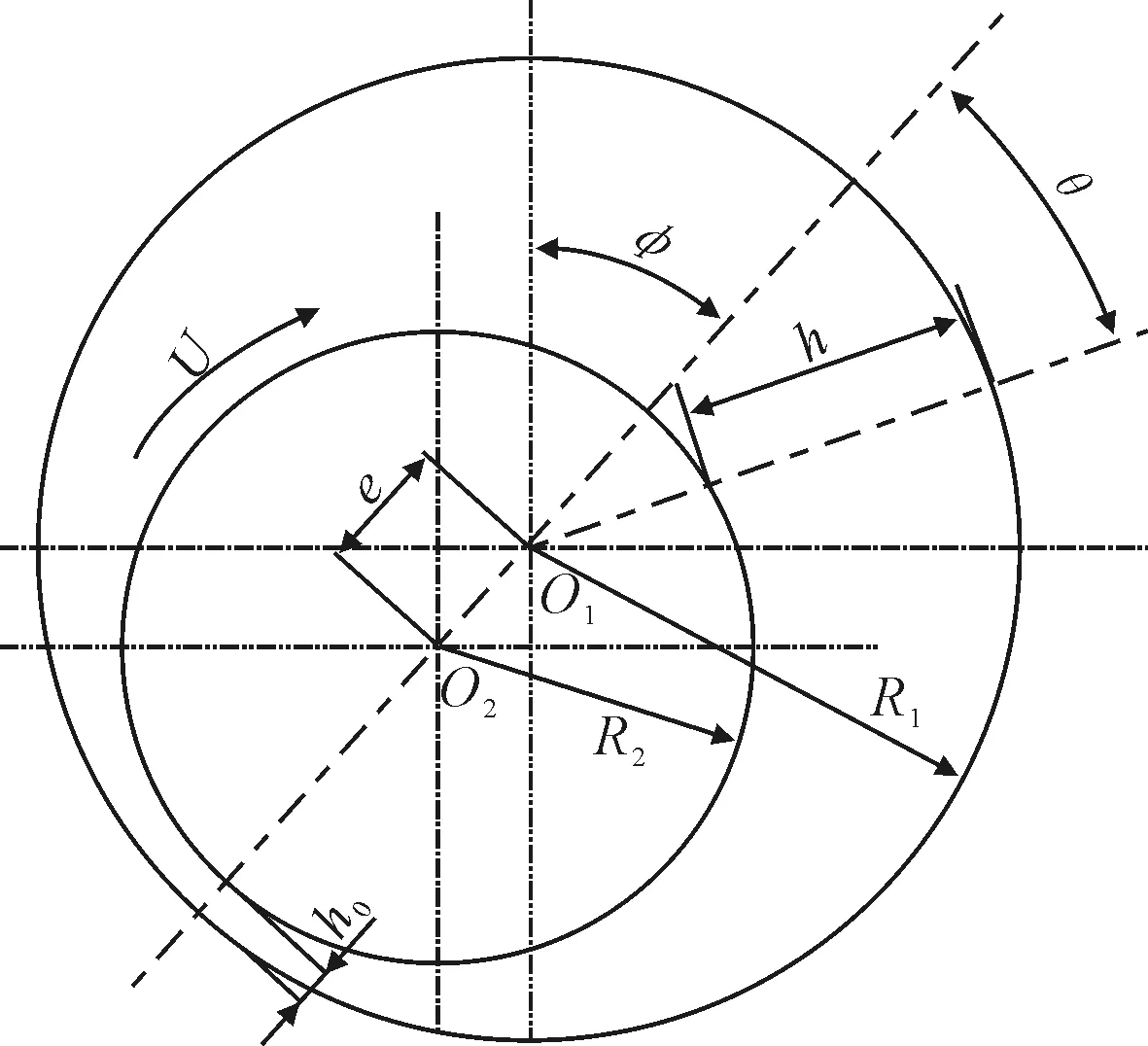
图2 油膜厚度示意

式中：c——半径间隙，c=R1-R2；

R1，R2——轴承轴瓦内半径和轴外半径；

e——偏心距，e=R1-R2-h0，h0为初始最小油膜厚度；

θ——圆周坐标；

δ1，δ2——滑动轴承内表面和曲轴外表面的随机粗糙度高度。

1.4 表面形貌影响因素

φx和φy分别为x和y方向上的压力流量因子，表示粗糙表面间的平均流量与光滑表面间的压力流量之比[3]。其表达式为

(3)

φy(H,γ)=φx(H,1/γ)

(4)

式中：C、γ——参数,取值参照文献[4]；

H——膜厚比，其定义为名义油膜厚度与综合粗造度的比值，表达式为

(5)

其中：σ1、σ2——两配合面粗糙度的公差；

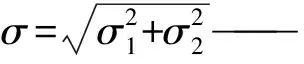
h——名义油膜厚度。

剪切流量因子φs反映两粗糙表面相对滑动时产生的附加流量的影响，其表达式为

(6)

式中：a1，a2，a3，A1和A2均为系数，取值参照文献[5]。

1.5 边界条件

对于中间轴承，可认为入口边界和两侧边界上压力等于供油压力，即p=0.1 MPa。出口边界通常采用Reynolds边界，即压力油膜的终点在最小间隙后的油楔发散区内的某个位置θ2，则对于宽度为B的中间轴承边界条件为

压力油膜起点：

θ=θ1，p=0.1 MPa。

压力油膜终点：

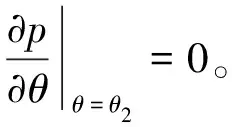
轴承两侧边界

y=0,p=0.1 MPa;

y=B,p=0.1 MPa。

1.6 轴承载荷

基于BV043/85建立基于时域的中间轴承抗冲击模型，获得冲击载荷作用下作用在轴颈上的动载荷。

2 Reynolds方程数值求解

2.1 Reynolds方程离散

采用中间差分格式离散Reynolds方程。离散方程形式为

(7)

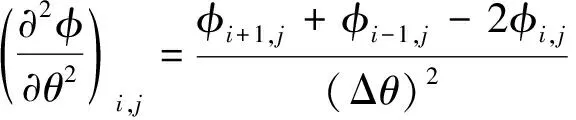
(8)

式中：φ——所求的未知量。

网格划分见图3。

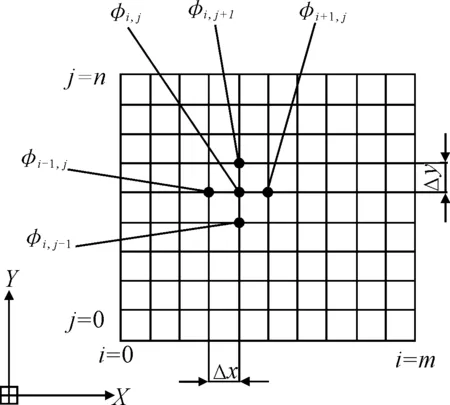
图3 网格划分示意

利用差分方法在求解域内将离散化的Reynolds方程应用到每个待求节点上，得到一组非线性方程，此外，加上边界条件，则未知量数目与方程数目相一致，方程组可以求解。

2.2 计算过程及流程图

冲击载荷作用下中间轴承流体动压润滑模型程序计算流程图见图4[6]。

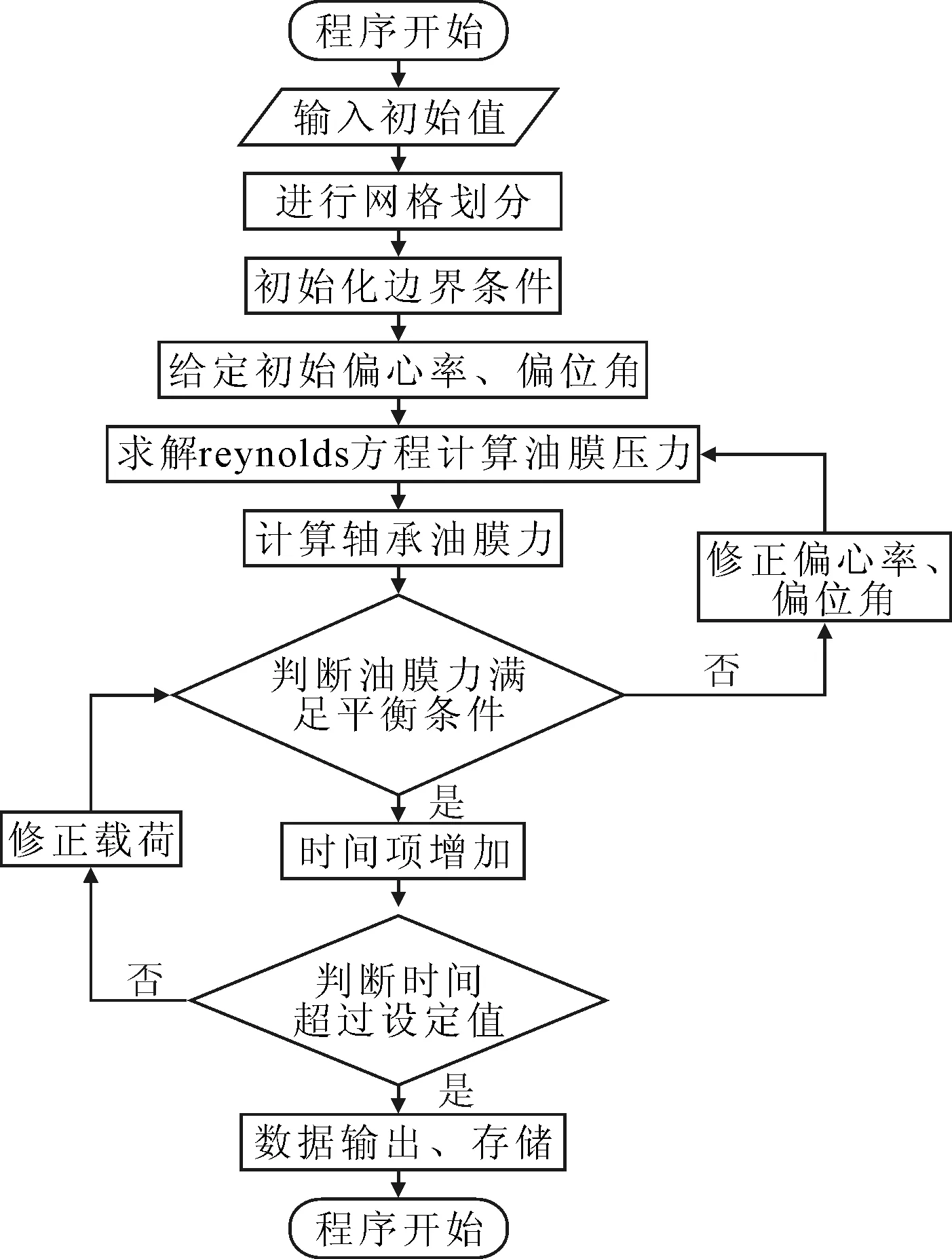
图4 中间轴承流体润滑计算流程

由图4可见，程序初始化阶段完成参数输入、网格划分等。在某一计算时间步的载荷下判断Reynolds方程是否求解收敛是通过判断载荷是否达到收敛条件来确定的。载荷大小与方向收敛判别公式为

(9)

|φload-φoil-180|<εangle

(10)

式中：F——油膜合力；

W——中间轴承载荷；

φload——载荷方向角；

φoil——油膜合力方向角；

εload——载荷收敛精度；

εangle——载荷方向角度收敛精度。

通过修正最小油膜厚度使油膜合力与载荷大小满足式(9)的判别条件；通过修正偏位角使油膜合力与载荷方向满足式(10)的判别条件。

上述两个判别条件是用来判断求解是否满足收敛条件的，如果计算不满足上述条件，则需修正最小油膜厚度值和偏位角值。

3 算例

以某中间轴承为研究对象，对其在冲击载荷作用下流体润滑性能进行分析。中间轴承相关计算参数见表1。

表1 计算参数

为分析工况参数对轴承润滑性能的影响，本文对150 r/min下受冲击载荷的润滑性能进行分析，并与稳定载荷工况下中间轴承的各项润滑性能进行对比。

3.1 冲击载荷输入

图5为基于BV043/85获得的冲击载荷作用下轴承在轴颈上的冲击载荷输入谱。

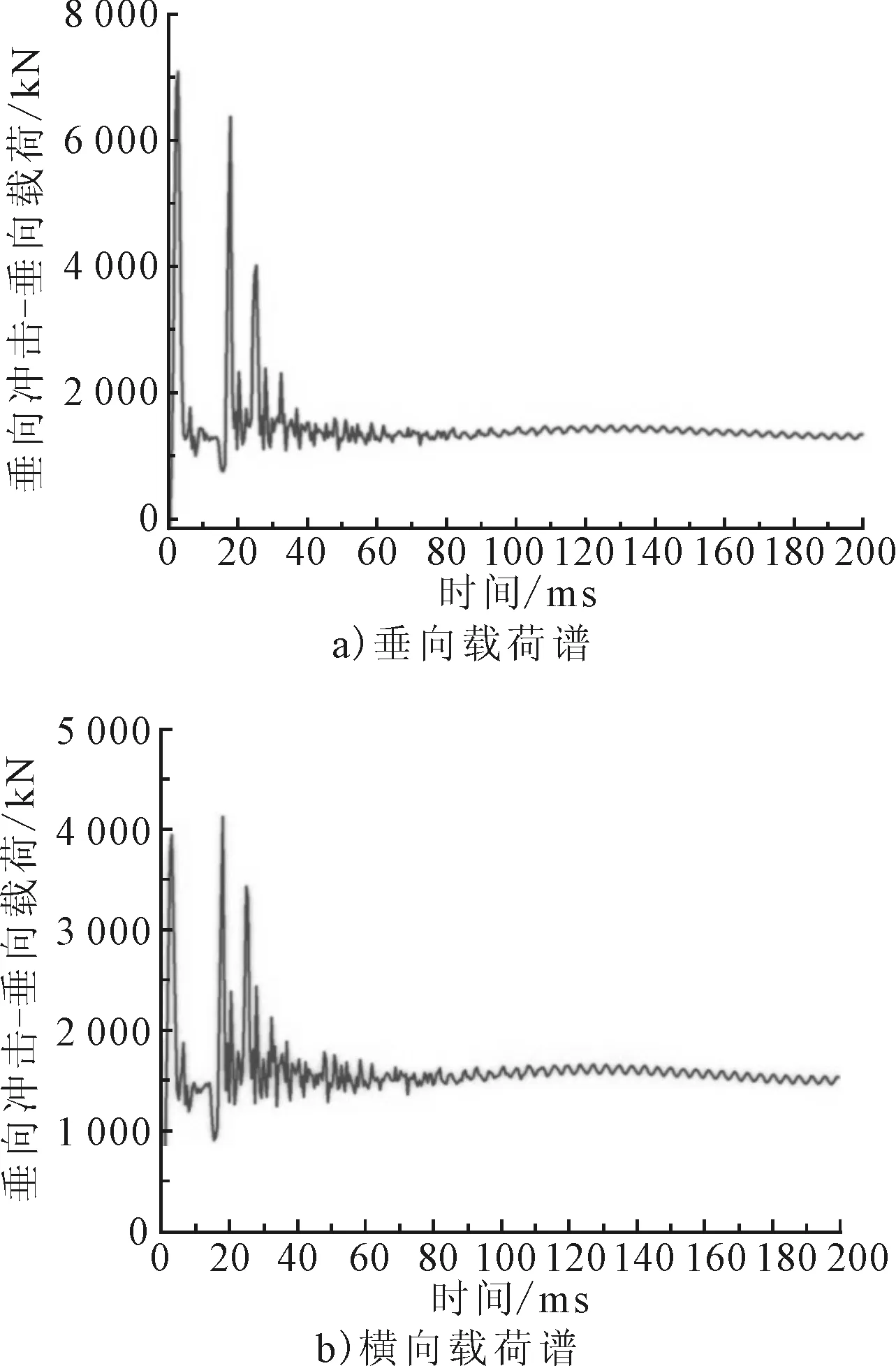
图5 冲击载荷谱

3.2 冲击载荷作用下轴承性能分析

1)最小油膜厚度。150 r/min转速时在上述冲击载荷作用下计算得到的中间轴承最小油膜厚度变化见图6。

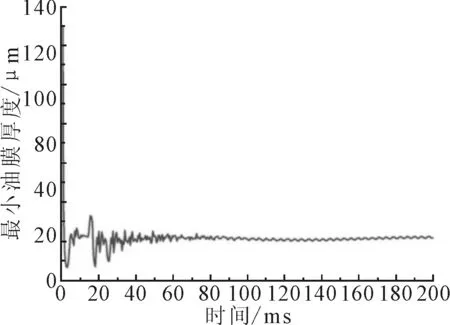
图6 冲击载荷作用下中间轴承最小油膜厚度随时间变化

2)轴承轴心轨迹。150 r/min转速时在冲击载荷作用下得到的中间轴承轴心轨迹分布见图7。

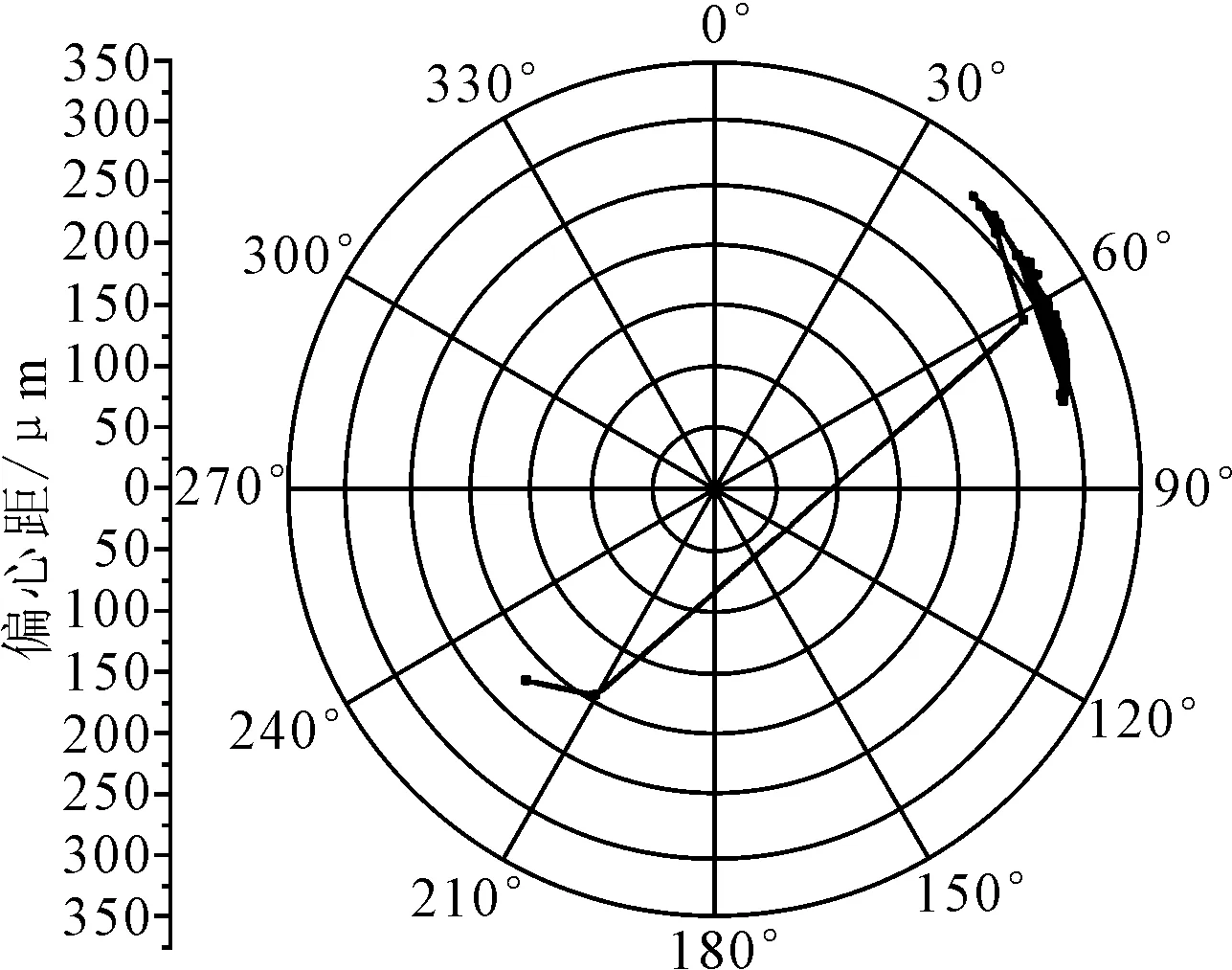
图7 冲击载荷作用下中间轴承轴心轨迹分布

3)摩擦力。150 r/min转速时在冲击载荷作用下计算得到的中间轴承摩擦力随时间的变化关系见图8。

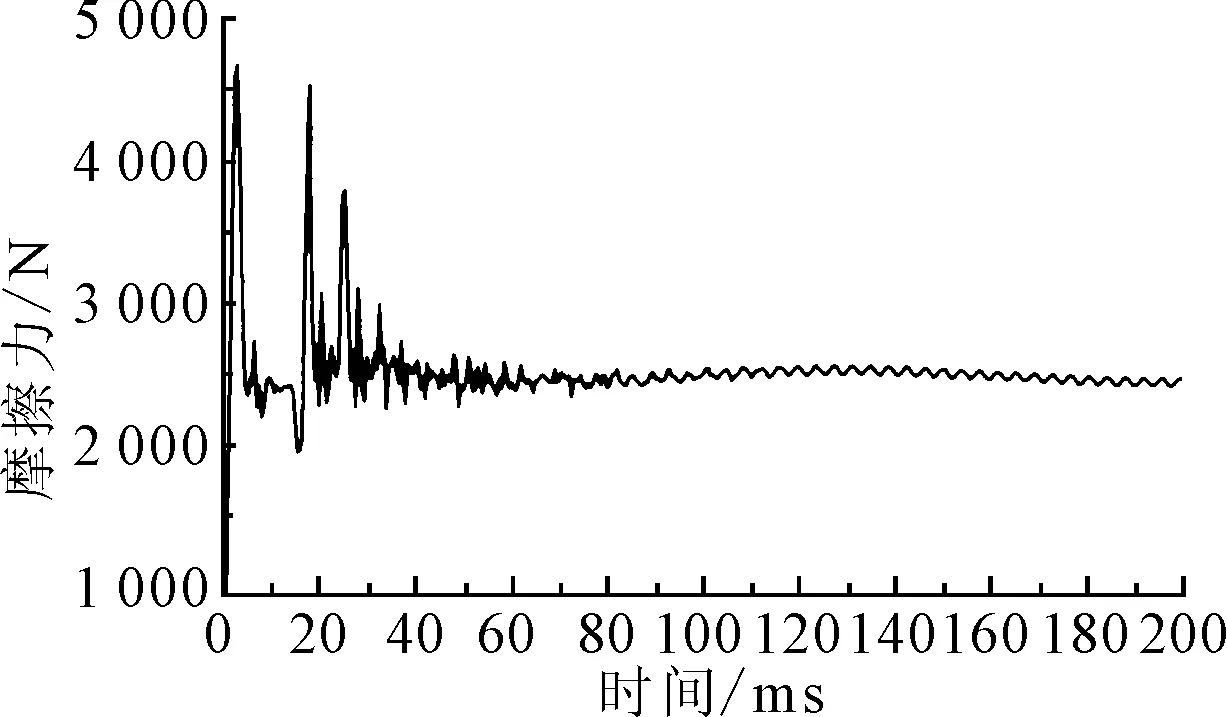
图8 中间轴承摩擦力随时间变化

分析计算结果可知，在冲击开始时，轴承承受的载荷波动较大，因此最小油膜厚度、摩擦力也随之波动较大，随着冲击载荷衰减至稳定后，轴承的相关参数分布也随之稳定。

3.3 冲击载荷下与稳定工况下润滑性能对比

在冲击载荷作用下，中间轴承的最小油膜厚度值为6.87 μm，而稳定载荷工况时，中间轴承的最小油膜厚度为104.56 μm，虽然两者均大于两润滑表面的综合粗糙度0.894 μm值，处于完全流体润滑状态，但是稳定载荷下中间轴承的润滑状况明显好于冲击载荷作用时的情况。

4 结论

1)在轴承工作状态下，受到外界冲击载荷作用时，轴承油膜随着载荷的变化会产生较大的波动，但是只要冲击时最小油膜厚度大于两接触面的综合表面粗糙度3倍以上时，就能够保证轴承的正常润滑工作。

2)当承受冲击载荷作用时，中间轴承油膜厚度会远远小于平稳运转时的厚度。因此在中间轴承润滑性能设计时，应考虑冲击状态下轴承安全工作的余量;轴系设计时应避免轴系出现共振。

3)中间轴承润滑性能还与轴系转速密切相关，在低速状态下，轴承建立油膜较为困难。因此在自润滑轴承设计时，还应考虑最低使用转速工况，以确保轴承能够安全可靠运行。

[1] 马艳艳,李桂国.动载滑动轴承润滑设计计算的研究进展[J].润滑与密封,2003(4):96-98.

[2] 温诗铸，黄 平．摩擦学原理[M]．2版．北京：清华大学出版社,2002.

[3] 王晓力,温诗铸,桂长林.基于平均流动模型的广义雷诺方程[J].润滑与密封,1998(3):16-18.

[4] PATIR N,CHENG H S.An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J].Transaction of ASME,Journal of Lubrication Technology,1978,100(1):12-17.

[5] PARIR N,CHENG H S.Application of average flow model to lubrication between rough sliding surfaces[J].Transaction of ASME,Journal of Lubrication Technology,1979,101(2):220-230.

[6] 李 震,桂长林,李志远,等.变载荷作用下轴-轴承系统动力学行为研究[J].机械设计与研究,2005(1):12-16.