机舱平台附近居住舱室自噪声特性分析

,, ，，

(哈尔滨工程大学 船舶工程学院，哈尔滨 150001)

船舶噪声会引起船舶结构疲劳破坏，同时也会使船员感到身体不适，从而使船员不能正常工作，降低精密仪器设备的适用寿命。若在已建好的船舶上再考虑降低噪声，这使其成本提高好几倍[1]。为此，首先将船舶声学设计融入到船舶结构设计当中。

目前，较为常用的船舶舱室噪声预报的方法是：在低频段内通过有限元[2]结合边界元的方法；在中高频段内则采用统计能量分析方法[3]。其中有限元结合边界元的方法对声学网格的要求较严格：一个声波波长必须至少满足6个声学网格的要求，从而无形中加大了声学模型计算规格，限制了计算频率范围[4]。统计能量分析方法可用于求解高频随机激励作用下的复杂工程结构的动力响应，该方法能够将复杂的机械系统或者声学系统划分为不同的模态群，从统计意义上将大系统划分为若干个独立的子系统，并不是逐个精确地确定每个模态的响应[5]。该方法能够充分利用在高频段上振动与声辐射的模态密集性，适用于解决复杂系统宽频动力学问题，能够将振动声源和空气声源有效地合理地模拟，同时可实现声学复合材料地有效定义及常规的减声降噪措施。

本文基于统计能量法，建立某船舱室统计能量法计算分析模型，对其机舱平台附近居住舱舱室噪声特性及优化进行数值分析研究。

1 计算分析模型

根据相应的图纸，在有限元软件中建立有限元模型。该船模型长69 m，型宽8.7 m，型深5 m，船壳厚度为8 mm，加强肋板厚度为6 mm,主船体材料为钢材，上层建筑材料为铝合金。材料的弹性模量为210 GPa，泊松比0.3，密度7 800 kg/m3；铝合金弹性模量为71 GPa，泊松比为0.33，密度为2 700 kg/m3。通常在实际计算模型中，考虑到流固耦合[6]的作用，可对船体材料密度作适当的加大处理。

将建立的有限元模型导入到VAONE中，并且相应的建立统计能量分析模型，全船统计能量分析模型中实际接收和传递能量的子系统共有801个，其中板壳子系统有726个，声腔子系统有75个，在子系统完全建立后，可得到某船的全船舱室噪声SEA初步分析模型，见图1～4。

图1 某型船SEA板壳子系统

图2 船舶子系统能量传递示意

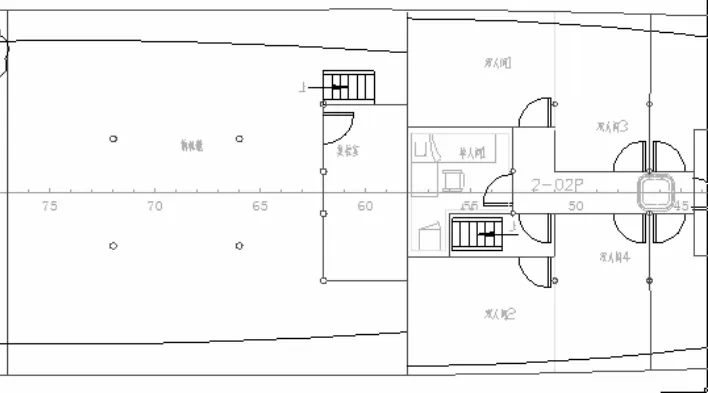
图3 某型船机舱附近居住舱室模型示意

图4 某型船机舱附近居住舱室SEA声腔简化模型

基于统计能量法[7]计算振动和噪声时，根据模态相似的原则将某型整船划分为801个子系统，包括船体甲板、舱壁、外板以及各个舱室声腔。当振动激励源作用在某个或某些子系统上时，子系统间通过接触边界会发生能量交换，对于每个子系统可得到一个能量平衡方程，最终形成一个高阶线性方程组，求解方程组可得到各个子系统的能量，根据求得的能量从而可获得相应参数如速度、加速度和外场声压等。

根据能量守恒原则，得到高阶线性能量守恒方程。

(1)

式中：ω——计算频带的中心频率；

UN——外界向该系统输入的功率；

n——该系统在某频段内的模态数；

ηi——子系统的内部损耗因子；

ηNi——子系统间的耦合损耗因子。

通过求解此方程组得到各个子系统的能量，再根据求得的各子系统能量对系统的响应进行估计预报。

每一个结构子系统或声学子系统都具有一个与时间平均和空间平均振速或声压成比率的稳态能量水平。

对结构子系统，它的振动均方速度为

(2)

式中：Ei——子系统结构的模态振动能量;

Mi——子系统质量。

振动速度级为

(3)

式中：v0——参考速度值，v0=1×10-9m/s。

据此相应的可求出系统的加速度级。

对声场子系统，其声压均方值为

(4)

声压级为

(5)

式中：p0——水介质中的参考声压，

取p0=1×10-6Pa。

由此建立能量与响应之间的关系，由能量可得到响应量，由响应量亦可计算出能量。

2 机舱附近居住舱室单人间噪声特性分析

从建立的分析模型可知，全船的损耗因子并没有给定，在此根据实际的工程经验，暂定全船的损耗因子为0.001。在此假定的基础上，对某型船的机舱平台附近居住舱室进行噪声特性分析。

采用统计能量法首先必须验证其是否满足计算条件，即所有子结构的模态密度都必须大于或者等于4。图5给出了相应部分子结构的模态密度，通过分析可知，大部分子结构的模态密度都大于7，因此采用统计能量法分析目标舱室的噪声是有效可行的。根据相关的船舶减振降噪的经验，机舱平台附近的居住舱室噪声的噪声源类型分为以下两类：螺旋桨噪声源及机械载荷噪声源。在此根据已确定的噪声源类型，整理出本船的主要载荷，本船在正常巡航状态下，所有相关的设备都正常运行。关于机械载荷，主要有主机、发电机、风机、泵类及空压机5种。对于螺旋桨噪声源，通常只需要考虑螺旋桨的振动激励载荷。

图5 部分子系统的模态密度

主要设备激励载荷布置位置见表1。

表1 主要设备激励载荷统计表

在验证其满足计算条件后，将以上14种载荷进行相对应的噪声源类型分类，再将这些载荷对于机舱平台附近居住舱室噪声的影响分别进行计算分析。将这些噪声源分成5种工况进行研究分析：只开主机与发电机、只开螺旋桨、只开风机、只开泵、所有激励载荷全开。5种工况下机舱平台附近单人间的噪声声压值见表2。

表2 5种工况下对机舱平台附近居住舱室单人间噪声声压值

通过分析表2可知，5种不同工况下对机舱平台附近居住舱室单人间的舱室噪声的影响不一样。可以看出，在所有载荷全开的工况下，单人间在频点63 Hz下的舱室噪声值最大。比较其他4种单机工况可知，只开主机与发电机对单人间的舱室噪声的贡献量最大;风机对其贡献量最小。因此可以得出主机与发电机载荷噪声源是机舱平台附近居住舱室单人间的主要噪声源。全船在所有激励载荷全开的工况下，全船结构的振动能量主要集中在前后机舱的附近。由船体板壳子系统的能量传递原理可知，结构振动能量是通过设备的基座传向内部声腔。能量在传递的过程中都会有耗散，所有的激励载荷源对其附近的舱室噪声的贡献量最大,因此，单人间的主要噪声贡献量来源于主机舱。主机、发电机载荷是居住舱室单人间的主传导途径。在全船激励载荷全开的工况下，单人间的舱室噪声值为78.6 dB,而居住舱室噪声限值为60 dB，因此单人间噪声声压不达标。

3 机舱附近居住舱室单人间噪声优化研究

对于不满足考核标准的舱室需要进行减振降噪[8]的优化工作。由于各舱室的舱室噪声与其主要噪声源及结构布置密切相关，所以对考核舱室噪声的减振降噪措施不能一概而论，而应从噪声源控制、提高传递损失、舱室末端防护等3个方面进行综合考虑，其优化方案如下。

1)噪声源控制。对主要的振动噪声源进行相应的隔振处理。在此次进行舱室噪声预报分析计算时，所加的主要振动载荷输入都是已经过隔振以后的数值，所以在此次预报计算中已对噪声源进行了控制。

2)提高传递损失。通过对舱室噪声的主传导途径的分析，主机及发电机为单人间舱室噪声的主传导传递途径。根据能量传递原理，在传递途径中会有能量的耗散及被材料吸收，故通过增大材料的损耗因子，使能量在传递途径上更多地被吸收，使传递到目标舱室的能量最小。

3)舱室末端防护。当振动能量传递到单人间舱室时，可在舱室内敷设吸声材料，吸收能量，降低舱室的自噪声。

通过以上3项优化措施的分析，初步确定3种优化方案如下。

1)将整船的模态损耗因子增大到0.01，使能量在传递的途径中损耗更多的能量，从而到达单人间的能量最少，以降低目标舱室自噪声声压级。

2)在单人间舱室敷设矿物棉板贴布板，当能量传递到目标舱室时，矿物棉板贴布板吸收部分能量，从而使目标舱室的噪声声压级降低。

3)在在适当改变模态损耗因子为0.004的基础上，在单人间舱室敷设矿物棉板贴布板。

表3为将整船的模态损耗因子定为0.01时在63 Hz考核频点下船舶单人间的舱室噪声声压级。表4为在居住舱单人间加矿物棉板贴布板后单人间的舱室噪声声压级。表5列出了将整船的模态损耗因子定为0.004且在目标舱室内敷设吸声材料矿物棉板贴布板下船舶舱室单人间的噪声声压级。图6给出了3种不同优化措施方案下居住舱单人间舱室噪声声压。

表3 整船模态损耗因子为0.01时的噪声声压级 dB

表4 在单人间加吸声材料的噪声声压级 dB

表5 模态损耗因子为0.004时加吸声材料的噪声声压级 dB

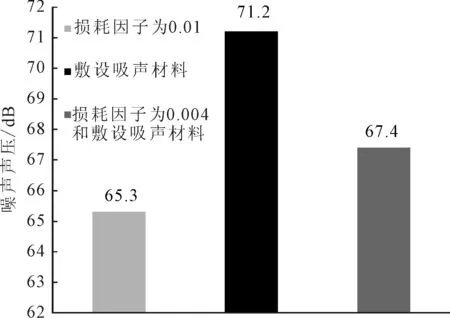
图6 3种不同优化措施方案下单人间的舱室噪声声压

通过比较表3和表4可知，将整船的模态损耗因子定为0.01和在单人间敷设吸声材料都能达到一定的降噪效果，都能达到考核目标要求，前者比后者的吸声效果更好。但是敷设吸声材料的经济效益比改变损耗因子要好。所以在满足设计要求的前提下，应该从考虑经济效率出发，在适当地改变损耗因子的基础上结合舱室敷设吸声材料也能达到不错的降噪效果，所以第三种方案为最佳优化方案。

4 结论

1)机械载荷激励源中的主机及发电机振动噪声源是机舱平台附近居住舱室单人间的主要噪声源，分析可知，不同的载荷激励源对居住舱室单人间的噪声贡献量不一样。

2)在确定了主要噪声源的基础上，得到居住舱室单人间的舱室噪声的主导传递途径，并且根据舱室分布，得出离单人间舱室越近，则对单人间居住舱室自噪声影响越大；

3)通过对3种优化方案的对比分析可知，第一种方案的降噪效果最好，其次是第三种方案，最后是第二种优化方案。从经济效应及可行性出发，得出第三种方案为机舱平台附近居住舱室单人间自噪声最优化的降噪方法。

[1] А.С.НИКИФОРОВ.船体结构声学设计[M].北京：国防工业出版社，1998.

[2] 王玉红.船舶上层建筑舱室噪声预测[D].哈尔滨：哈尔滨工程大学，2003.

[3] 姚德源，王其政.统计能量分析原理及其应用[M].北京：北京理工大学出版社,1997.

[4] 张 立，基于国际新规范的舱室噪声预报及控制技术研究[D].哈尔滨：哈尔滨工程大学，2012.

[5] 和卫平，陈美霞，高 菊，等.基于统计能量法的环肋圆柱壳中、高频振动与声辐射性能数值分析[J].中国舰船研究,2008，3(6):7-12.

[6] 愈孟萨，朱正道.集成统计能量法计算声纳自噪声水动力噪声分量[J].船舶力学,2007,11(2):274-283．

[7] 伍先俊，朱石坚.统计能量法及其在船舶声振预测中的应用综述[J].武汉理工大学学报，2004，28(2):212-215.

[8] 朱石坚，何 琳.船舶减振降噪技术与工程设计[M].北京：科学出版社，2002.